例析提升学生数学学习能力的有效途径

江苏省泰兴中学 (225400) 李建新

提升学生的关键能力与核心素养的本质就是全面提升数学教与学的效益,更确切地说,就是提升高中生在学习数学过程中对数学知识的理解能力,以及学生的思维能力、分析能力、解决问题的能力等学习数学过程中所需要具备的能力．

为了提升高中生的数学学习力,应该结合高中数学教学的特点,在教学知识的过程中,给予学生更多的主体性,发挥主观能动性,深入到理解能力、思维能力、分析能力以及解决问题能力,有效提升数学学习力．

1．发展思维,拓展学生的思维能力

良好的思维能力是学生必须具备的一种基本能力,涉及观察、分析、归纳、推理等能力．在高中阶段的数学教与学过程中,教师可以借助多种方式来有效发展学生的思维,拓展学生的思维能力,其中“一题多解”、“一题多变”、“多题一解”等形式都可以很好达到目的．

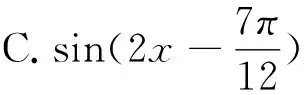
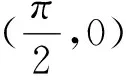
借助以上的教学形式,对于学生的思维能力的拓展与提升具有重要意义．“一题多解”,可以开阔学生思路、发散学生思维,使学生学会多角度分析和解决问题;而“一题多变”,可以加深学生对数学原理、通性通法的认识,提高解题技巧与能力．在变式中寻找通法,在探究中升华能力,研究之路定会越铺越远．

2．全面开花,培养学生的分析能力

良好的分析能力也是学生必须具备的一种基本能力,涉及分类分析、对比分析、比较分析等能力．在学习过程中或是问题解决时,需要根据不同的知识场景与问题情境等进行分析,从而找出解决问题的方向与方法．

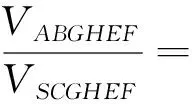
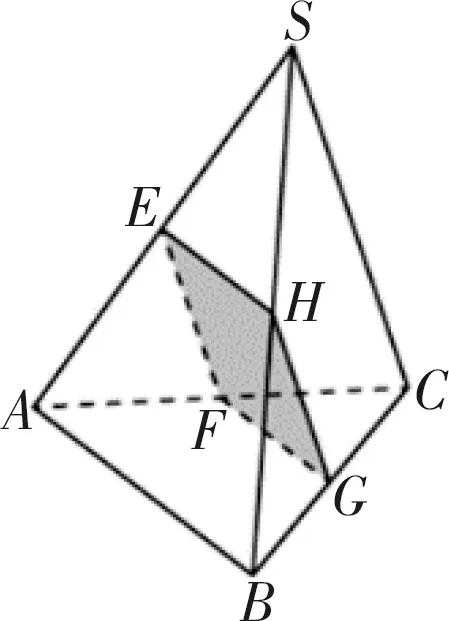
图1

在实际讲授该问题时,关键就是引导学生正确分析问题,挖掘问题的内涵与实质．一方面可以直接切入,通过常规思维来分析;另一方面可以抽象与提升场景,通过特殊空间几何体的结构特征来分析．

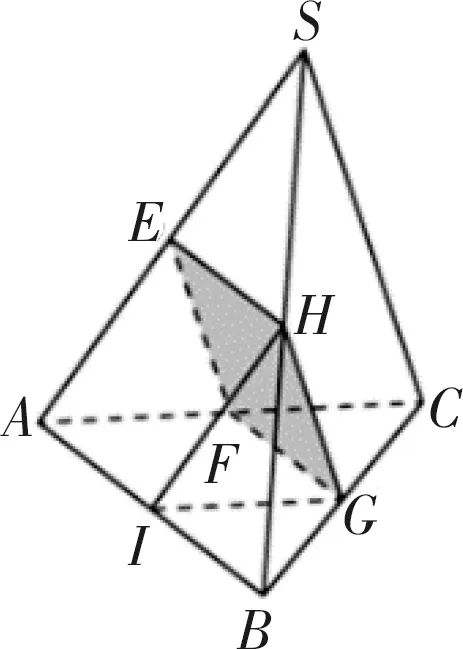
图2

方法2：(特殊形状法)由于图形不确定,而答案固定,故假设该三棱锥为正四面体,则所截得的两部分形状一样,则对应的体积相等,即=1,故答案为1．

借助不同的分析视角,或从常规问题的解决入手,利用三棱锥的体积公式以及空间几何体的变化特征来转化,可以达到分析与求解的目的;而进一步抽象问题,并加以提升,可以从特殊的正四面体入手,利用空间图形的结构特征来快速分析,效果更加良好．

3．循序渐进,提升学生的解决问题能力

良好的解决问题能力是学生必须具备的各种基本能力的总体现,涉及转化问题、模拟解决问题、应用知识解决问题等能力．在实际学习过程中,要将陌生、复杂的问题等通过转化、模拟、应用等方面,转变为熟知、简单的问题来处理,实现问题的最终解决．

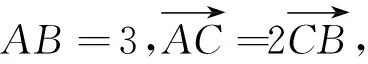
分析：根据题目条件,利用平面向量的线性关系式确定线段上三点的比例关系,利用平面向量的数量积公式与条件加以转化,确定PC为∠APB的平分线,借助三角形的角平分线定理以及余弦定理的应用,最后利用同角三角函数基本关系式来确定sin∠PAB的最大值．有效结合各部分知识与技能的联系来分析问题,进而得以正确解决问题．

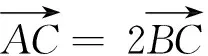
点评：问题中,平面向量的概念、运算、数量积等的几何意义中涉及三角函数(或解三角形)等相关知识,这也为三角函数(或解三角形)和平面向量的综合问题进行无缝链接,实现不同知识之间的交互与整合．有效提升解决问题能力的关键就是巧妙融合“四基”能力,交汇不同的知识与思想方法,达到全面渗透,综合应用．

为了有效解决问题,学生须系统掌握数学基础知识以及基本技巧,结合具体问题场景,进行合理分析、转化、应用等,结合所学知识与所掌握技能来切入,才能够发现问题的解决方法．

总之,在高中阶段的数学学习过程中,有效提升高中生的数学学习力,要结合实际,从学生的理解能力、思维能力、分析能力和解决问题能力等视角切入,给予学生充分的练习机会,发挥学生的主体性,积极主动参与其中,能才充分得以不断提升与发展学生的数学学习力,真正落到实处,有效培养核心素养．