改进局部扩展的复杂网络重叠社区检测算法
付立东,刘佳会,王秋红
(1.西安科技大学 计算机科学与技术学院,陕西 西安 710054;2.中国电子科技集团有限公司第20所,陕西 西安 710068)
0 引言
重叠社区广泛存在于现实世界复杂系统中[1],研究重叠社区对揭示网络的真实结构、发现网络中所隐藏的复杂信息具有重要作用[2-3]。
目前,已提出多种不同类型的重叠社区发现算法,包括模块度优化方法、标签传播方法和局部扩展方法等。模块度优化方法可以得到较为准确的社区结构,但存在分辨率限制,即在模块度值最大时,往往无法发现小社区结构。标签传播算法时间复杂度偏低,但由于需要存储多个标签信息,耗费的计算资源较多。局部扩展方法无需网络的全局结构信息且种子扩展过程可以并行,算法效率较高,适用于大规模复杂网络[4],但算法的划分结果受种子质量的影响较大。
局部扩展方法旨在选取种子节点,通过种子节点的邻近节点对社区进行扩张[5]。当邻近节点的加入不能进一步提高社区质量时,扩张停止。局部适应度算法[6](Local Fitness Maximization,LFM)是经典的局部扩展模型,随机选择网络中的节点作为种子,并通过不断优化适应度函数来扩展种子,得到最终的社区划分。但由于种子选取的随机性,导致算法性能不够稳定。基于核心相似性的局部扩展算法[7](Local Expansion Based on Core Similarity,LECS)改进了LFM 算法中的种子选择和质量函数,提出节点中心度来选择高质量的种子。但由于该指标没有考虑节点的邻居之间不存在连边的情况,导致所选出的种子质量不高,影响了后续的网络划分。基于偏好的SAT社区检测 算 法[8](SAT-based Community Detection,CD-SAT)通过集成用户偏好来确定每个社区的质心,根据节点与质心的距离来构建社区,通过优化目标函数来确定最终社区的数量。贪婪耦合种子扩展算法[9](Greedy Coupled-seeds,GREESE)不同于上述算法,该方法在选取种子时不再依赖于单个节点,而是将耦合种子视为初始社区来扩展。但随机选择一个节点与其最相似邻居来构建耦合种子则会导致较多小社区的生成。
种子的质量对算法划分结果有很大的影响[10]。高质量的种子有助于社区扩展为一个完整的社区结构,而低质量的种子则会影响后续其他节点的扩展[11],从而使整个网络的社区划分精确度不高。扩展策略设计的好坏也会影响社区的扩张。目前,大多数的扩展策略是以一个种子为一个初始社区,然后运行质量函数的贪婪优化过程来扩展社区[12],而质量函数的设计主要基于社区内部节点之间的连通性[13],忽略了社区外部节点的影响。
因此,为有效度量种子质量和确定节点的社区归属,从节点的度和邻域节点之间的连通性的角度改进局部扩展方法的种子选择和社区扩展。算法主要在3个方面进行改进:①融合节点度和邻域结构紧密性定义节点凝聚度指标,寻找高质量的种子;②综合考虑节点在社区内部和社区外部的拓扑结构信息,提出社区归属度和归属阻力来扩展节点;③扩展结束后,增加社区边界节点检查调整,通过节点移动来调整节点与社区之间不准确的归属关系。
1 相关理论
假设网络G=(V,E),邻接矩阵为A,那么对于网络中的任意2个节点u,v,如果2个节点存在一条边,则Auv=1,否则Auv=0。
1.1 社区邻居
社区邻居是相对于节点邻居而言,如果社区外的一个节点u与社区内的节点存在连边,则把节点u看作社区的邻居。社区外所有与社区内的节点存在连边的节点构成的集合定义为社区邻居集,主要作为扩展阶段的候选节点[19],见式(1)。
式中 V为网络中的节点集合;C为节点v所在的社区。社区邻居不包括种子的邻居。
1.2 边界节点
陈界全等给出了边界节点的数学定义,即对于网络G的社区划分C={c1,c2,…,cn},若v∈ci,u∈cj,ci≠cj且Auv=1,则称节点v和节点u为边界节点[16]。
2 改进的局部扩展算法
主要针对无向复杂网络进行研究,算法包括3个主要的过程:首先利用节点凝聚度指标来度量节点对周围邻居的局部凝聚力,并根据其全局排名选取种子;然后利用社区归属度及归属阻力指标对种子及其邻居形成的核心区域进行扩展;最后基于社区边界节点调整策略移动不合理的边界节点,修正节点与社区之间不准确的归属关系。
2.1 种子选择
种子的质量对社区发现结果有很大的影响。为快速有效地选择出种子,最常用的方法是基于节点度去衡量种子质量。节点度[17]描述的是节点对其直接邻居的影响力,度越大表示其领导力越强。该方法虽然体现了一个节点的领导力,但无法度量该节点长久的影响力,当节点的邻居之间连边较少时,随着网络的演进,该节点则容易受到其他节点的吸引,最终失去其领导力。因此,仅从节点度的角度不能有效衡量一个节点对周围邻居的凝聚力。
KITSAK等提出节点对信息的传播能力不仅与节点度相关,而且与节点的邻域结构紧密程度相关[18]。具体来说,节点度越大,邻域结构越紧密,节点的传播能力越强。因此,应综合考虑节点度和邻域结构紧密性来选取种子。节点的聚类系数[19]量化了其邻居节点之间相互聚集形成社区的程度,可以用来衡量节点邻域结构的紧密性。节点聚类系数越大,表明邻居之间的连边越多,其联系越紧密。无向无权图中,节点vi的聚类系数的定义见式(2)。
式中 Ni为节点的邻居集;di为节点的度;Ci=0表示节点vi的所有邻居之间都不存在连边;Ci=1为节点vi的所有邻居之间都存在连边。
为提高种子选取的效率,对节点聚类系数进行简化,利用邻居节点之间存在连边的数量来表征节点邻域结构的紧密性。考虑到只利用邻域结构紧密性不能处理邻居之间无连边的情况。因此,结合节点度和邻域结构紧密性来度量一个节点的凝聚力,根据节点凝聚度值对节点降序排列,并构成优先级列表,依次选取列表中的第一个节点即节点凝聚度最大的节点作为种子。节点凝聚度定义如下。
定义1 节点凝聚度
该指标不仅考虑了节点的邻居之间联系的紧密性,而且增加了节点度信息来处理节点的邻居之间不存在连边的情况,从而使该指标选择出的节点更具有代表性,见式(3)。
式中 D(v)为节点v的凝聚度;Nv为节点v的邻居集;dv为节点的度。
以图1为例,仅考虑邻域结构紧密性来计算节点的凝聚度,未分配节点降序排列在集合S={v3,v2,v1,v0}。若依次选取S中未分配的节点及其邻居形成初始社区,则会生成3个小社区即C2={v3,v0}、C3={v2}、C4={v1}。结合节点度和邻域结构紧密性来计算网络中未分配节点的凝聚度,节点v0的凝聚度大于节点v1,v2和v3,因此节点v0优先成为初始社区的种子,吸引节点v1,v2和v3的加入,从而防止了小社区的生成。因此,将节点度和邻域结构紧密性相结合,可以选出高质量的种子,减少低质量社区的生成。
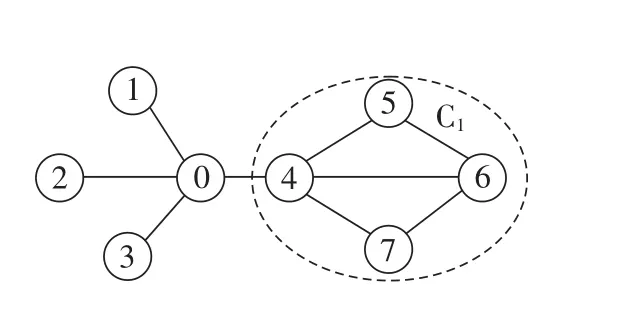
图1 合成网络G1Fig.1 Synthetic network G1
2.2 社区扩展
基于优先级列表,对选取的种子进行局部扩展。首先将种子及其邻居看作初始社区,根据社区归属度及归属阻力对不合理的种子邻居进行清洗,以得到与种子联系较紧密的核心区域。然后寻找核心区域的社区邻居,并根据社区归属度及归属阻力对其进行扩展,如果形成社区,从优先级列表中删除社区内的节点,否则从优先级列表中删除选取的种子。重复上述步骤,当优先级列表为空时得到多个重叠社区。下面对社区归属度和归属阻力进行定义与分析。
社区归属度指标用于描述节点属于某个社区的程度。社区归属度值越大,社区对其吸引力越强。如果待加入节点在社区中的邻居数较多,且这些节点之间有较高的聚集程度,表明这个节点具有较大概率会加入这个社区。但一个节点是否会加入社区不但受社区内部节点的吸引,而且会受到网络中其余节点的影响,因为这些节点会阻碍节点的加入。因此,在扩展社区时,应同时考虑到网络中其余部分节点对该节点的归属阻力,通过对比两者的大小来决定一个节点的加入。因此,文中提出社区归属度和归属阻力的定义。
定义2 社区归属度
将节点在社区内的邻居数与内部邻居节点之间的连边数之和定义为社区归属度,见式(4)。
式中(Nu∩C)为节点u在社区内的邻居集;C为局部社区。
定义3 归属阻力
节点在社区外的邻居数与外部邻居节点之间的连边数之和定义为归属阻力,见式(5)。
式中(Nu∩G′)为节点u在社区外的邻居集;G′为社区外的节点形成的网络。
以图2为例来说明社区归属度和归属阻力在扩展节点时的应用。

图2 合成网络G2Fig.2 Synthetic network G2
根据社区邻居的定义可知,社区C1的邻居为v8和v9。根据式(4),节点v8加入社区C1的归属度M(v8,C1)=1,社区外的节点v8,v4,v7,v9构成的网络G′对节点v8的归属阻力R(v8,G′)=3。节点加入社区C1的归属度小于网络G′中节点对其加入的阻力,因此节点v8不能加入社区C1,等待后续扩展。同理,节点v9也不能加入社区C1。
2.3 社区边界节点检查调整
三支决策理论[21]与社区划分的结合为改进局部扩展方法提供了新思路[22-23]。基于三支决策理论,学者提出边界域中的节点由于信息量不完整可能存在重叠节点不合理,为获得更好的社区性能,设计算法时需考虑对边界区域中的节点进行二次划分[24]。
基于上述理论,提出社区边界节点调整策略,对分配不合理的边界节点或未发现的重叠节点,通过节点的移动来修正节点与社区之间不准确的归属关系,以得到准确率更高的社区划分结果。通过对比边界节点在各个社区中的归属度值来判断一个边界节点所在社区是否合理。社区边界节点调整策略针对以下3种情况。
1)边界节点在其他社区中的归属度大于原始社区中的归属度时,将边界节点调整到最大社区归属度对应的社区,并从原社区删除该节点。
2)归属度相等时,说明该边界节点是一个重叠节点,将该边界节点复制到归属度相等的社区。
3)原社区归属度大于其他社区归属度时,说明边界节点所在位置合理,不做操作。
2.4 算法实现
改进局部扩展的复杂网络重叠社区检测算法的实现包括种子选择、社区扩展和社区边界节点检查调整三个过程。种子选择过程的主要思想是以一种混合的方式来选出高质量的种子,并限制种子和已在社区内的节点再次成为种子。社区扩展阶段的主要思想是通过综合考虑节点在社区内部和社区外部的网络结构信息来扩展节点。社区边界节点检查调整过程的主要思想是在得到社区划分结果后,通过边界节点的移动来修正节点与社区之间不准确的归属关系,进一步提高算法性能。算法的具体实现如下。

3 时间复杂度分析
假设n,m,珔d,|C|,珔C分别为网络中的所有节点数、连边总数、节点的平均度、社区或检测出的社区数、平均社区大小。计算节点凝聚度的时间复杂度为O(珔d2),基于最大堆的未分配节点序列时间复杂度为O(n log n)。计算节点社区归属度的复杂度为O(珔d(log珔C+珔d))。扩展阶段的时间复杂度为O(n log n+|C|珔C珔d(log珔C+珔d))。设k表示边界节点数,边界节点检查调整阶段的时间复杂度为O(|C|k珔d2)。因此,文中算法的总时间复杂度为O(n log n+|C|珔C珔d(log珔C+珔d)+|C|k珔d2)。多标签传播算法(以经典的COPRA算法为例),其时间复杂度为O(|C|m log(|C|m/n)+|C|3n)。基于模块度的重叠社区发现算法[26](Detecting Overlapping Communities Over Complex Network Big Data,DOC),其时间复杂度为O(n log2(n)+n)。由于网络的总节点数n和总边数m要远大于社区数量和平均社区规模,因此,文中算法的时间复杂度低于上述2种算法。
4 试验与分析
为验证文中算法检测重叠社区的有效性,将所提算法与GREESE算法、LFM算法、LECS算法和CDSAT算法在合成网络和真实网络数据集上进行对比,对比算法的参数均设置为原论文中的最优参数。
4.1 评价指标
重叠标准化互信息NMI指标[6]来源于信息论中的熵,用于度量聚类结果的相似程度。NMI值越大,说明算法所发现的社区结构与真实网络结构越接近,见式(6)。
式中 H(X|Y)为X在Y上的规范化条件熵。
扩展模块度EQ指标[27]用于评估重叠社区发现算法的性能,EQ值越大,算法识别高度聚集的社区的性能越好,见式(7)。
式中 A为网络的邻接矩阵;m为网络的总边数;i为社区标号;ku,kv分别为节点u和v的度数;Ou,Ov分别为节点u,v所属的社区数量。
D-Score指标[7,14]用于评估算法发现的社区数量与真实社区数量之间的差异,见式(8)。
4.2 合成网络试验与分析
4.2.1 数据集
LANCICHINETTI等提出的LFR基准[28],常用于复杂网络社区发现算法的对比试验中。通过调节模糊参数、社区规模和重叠节点数生成3组合成网络数据集。具体见表1。

表1 3组合成网络的参数设置Table 1 Parameter settings of synthetic network about three groups
参数n为网络中的总节点数;|C|min为最小的社区规模;|C|max为最大的社区规模;MU为网络结构的清晰度,其值越大,网络中的社区结构越难以识别;On为网络中的重叠节点数。
4.2.2 试验结果与分析
5种算法在3组合成网络数据集上的性能采用重叠标准化互信息NMI和D-Score指标来评价。NMI值越大,算法检测的社区结构与真实分区越接近;D-Score值越小,算法所发现的社区个数与真实情况越一致。
LFR 1合成网络上的试验结果如图3所示,用于研究模糊参数对算法性能的影响。5种算法的性能都随模糊参数MU的增大而呈现不同程度的下降,说明5种算法的性能都受MU的影响,即网络结构清晰度会影响算法性能。
随着混合参数的不断变化,网络的结构特征也会发生变化。LFM、CDSAT和LECS算法通过对比质量函数指标值与特定阈值之间的大小来进行局部扩展时则会忽略每个网络的结构特征变化,从而导致所发现的社区结构与真实社区存在偏差,NMI值明显低于 GREESE 和文中算法。GREESE算法通过逐次迭代缩小阈值来发现高质量的社区,但由于寻找耦合的种子时采用了随机策略,所以其NMI值低于文中算法。
LFR2合成网络上的试验对比结果如图4所示,用于探究社区规模对算法性能的影响。从图4可以看出,随着社区规模的增加,5种算法识别真实社区的性能变差。LECS,LFM和CDSAT算法随社区规模的增加,其NMI值呈逐渐下降趋势,GRESSE和文中算法的性能基本不随社区规模的增加而下降。在社区规模为200时,LECS算法的NMI值最高,随着社区规模的增加,其性能低于文中算法。原因是文中算法的扩展规则是基于节点与社区成员关系的,社区规模越大,可利用的结构信息越多,越有利于算法识别社区结构。同时,文中所提出的边界节点调整策略也进一步提高了社区划分的质量。从表3可以看出,文中算法检测出来的社区个数与真实社区个数更趋于一致。

图4 LFR 2合成网络上NMI对比Fig.4 NMI comparison on LFR 2 synthetic network
LFR 3合成网络上的试验结果如图5所示,用于对比重叠节点数对算法性能的影响。从图5可知,5种算法的性能基本不受重叠节点数的影响,随着重叠节点数的增大,5种算法的NMI值走势比较平稳,不会随着On的增加而下降。原因是重叠节点通常远离社区的核心成员,其数量的变化基本不影响由特定种子确定的社区数量。这也体现了局部扩展方法在大规模网络中的优势。

图5 LFR 3合成网络上的NMI对比Fig.5 NMI comparison on LFR 3 synthetic network
从表2、表3和表4可以看出,LECS和LFM算法的D-Score值较大,明显高于其他几种算法,说明这2种算法识别出的社区数量与真实社区个数相差较大。GREESE,CDSAT和文中算法的D-Score值较小,说明这3种算法划分的社区个数与真实分区更接近。

表2 不同模糊参数下的D-Score对比Table 2 D-Score comparison on different fuzzy parameters
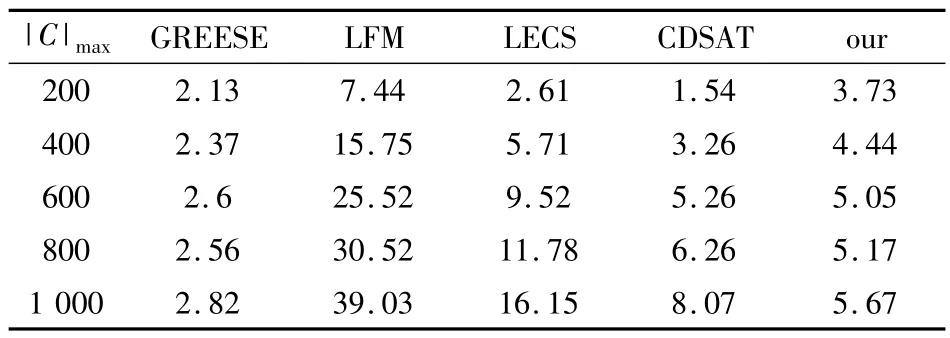
表3 不同社区规模下的D-Score对比Table 3 D-Score comparison on different size of community
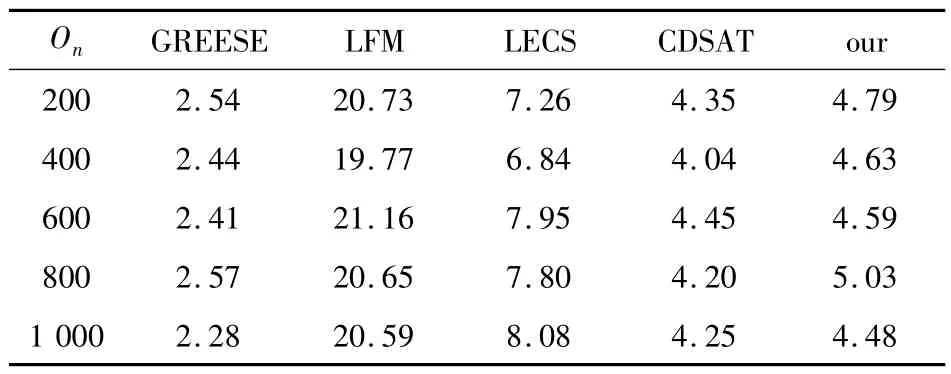
表4 重叠节点数变化下的D-Score对比Table 4 D-Score comparison under the change of the number of overlapping nodes
综合5种算法在合成网络和真实网络数据集上的NMI和D-Score值,文中算法的性能较对比算法更具有优势。
4.3 真实网络试验与分析
4.3.1 数据集
6个真实网络数据集的具体描述见表5。参数n为网络的节点总数;m为网络的连边总数;c为真实网络的社区个数;“-”为真实社区数量未知。
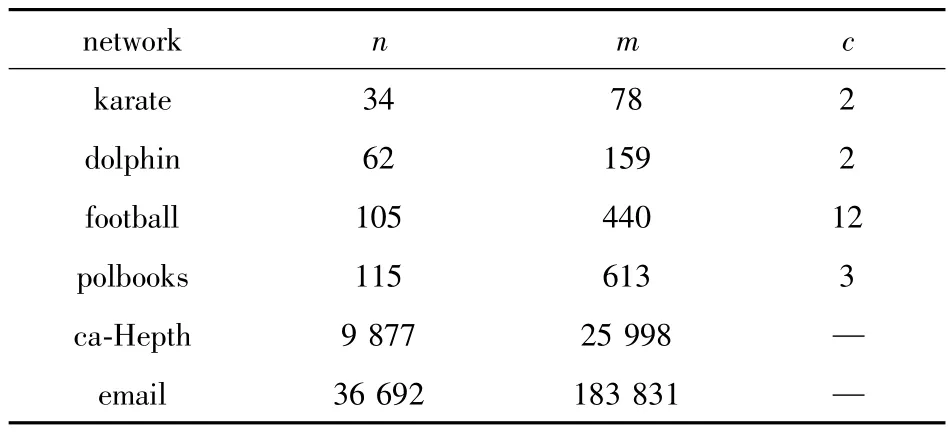
表5 真实网络数据集描述Table 5 Description of real network data sets
4.3.2 试验结果与分析
在6个真实网络数据集上,已知真实分区的网络采用扩展模块度EQ和D-Score指标评价算法性能,真实分区未知的网络采用扩展模块度EQ对比。
表6是5种算法在真实网络上的扩展模块度值,其中,average表示算法在6个网络上的平均性能。average值越大,说明算法在真实网络上的平均扩展模块度越高,其性能越好。

表6 真实数据集上的EQ对比Table 6 EQ comparison on a real data set
综合算法在6个真实网络上的平均性能来看,文中算法的扩展模块度达到0.483 1,明显高于对比算法,这说明文中算法可以识别真实网络中的重叠社区结构,性能较对比算法有一定的提高。
在已知真实分区的网络上,5种算法识别出的社区数量与真实分区之间的差异情况见表7。对比5种算法的D-Score值,文中算法在polbooks网络上的D-Score值略高于CDSAT算法,在karate、dolphin和football 3个网络上的D-Score值均最小,说明算法划分的社区数量更符合真实分区。

表7 真实社区结构已知的D-Score对比Table 7 D-Score comparison of real community structures
综合真实网络上的试验可知,文中算法的性能优于对比算法,可以有效发现网络中的真实社区,检测出的社区结构与真实情况更为一致。
4.4 社区边界节点调整策略对算法性能的影响
为验证边界节点调整策略的有效性,通过对比算法在3组合成网络上的重叠标准化互信息NMI值来说明该策略对算法性能的影响,结果如图6所示。former曲线表示未实施边界节点调整策略时的算法性能,later曲线表示算法扩展结束后实施了边界节点调整策略时的性能。

图6 边界节点调整策略对算法NMI值的影响Fig.6 Effects of boundary node adjustment strategy on NMI
观察图6中的红色曲线可知,在3组合成网络上,边界节点调整策略均使算法的NMI得到了不同程度的提高。这说明在扩展结束后,通过边界节点的移动可以修正节点与社区之间不准确的归属关系,得到更加合理的社区结构。其中,LFR 2和LFR 3合成网络中的NMI值较LFR 1合成网络有明显提升,说明边界节点检查调整策略对社区规模较大或重叠节点较多的网络提升效果更为明显。
5 结论
1)根据节点局部信息和全局排名,以一种混合的方法来选择种子,并对种子和已在社区内的节点限制其再次成为种子,可以得到质量较高的种子。
2)综合考虑节点在社区内部和外部的拓扑结构信息,设计一种新的扩展策略即利用社区归属度和归属阻力来扩展节点。这种方法同时考虑了社区内部节点的吸引力和社区外部网络结构对节点的归属阻力,可以更全面地确定节点的社区归属。
3)在得到社区划分结果后,通过社区边界节点的移动来修正节点与社区之间不准确的归属关系,可以进一步提高算法性能,对社区规模较大或重叠节点较多的网络提升效果更为明显。
4)合成网络和真实网络数据集上的D-Score和NMI值表明,文中算法划分的社区数量与社区结构更接近于真实情况。

