基于深度学习的低频宽带隔声器件设计∗
孙雪聪 贾 晗 杨玉真 杨 军
(1 中国科学院声学研究所 噪声与振动重点实验室 北京 100190)
(2 中国科学院大学 北京 100049)
0 引言
在日常的工作和生活中,噪声已经成为了一种随处可见的污染,时刻困扰着人们。噪声污染不仅会危害人们的生理健康,还会对人们的心理造成伤害。因此,随着人们对生活品质的追求越来越高,噪声问题逐渐成了人类社会不得不面对的一个重要问题。近年来,声人工结构逐渐成为吸隔声领域的研究热点。与传统材料相比,声人工结构的最大优势在于其可以利用亚波长尺寸的结构实现材料物理特性的调节以及对声波的调控,为解决低频吸隔声问题提供了新的技术思路[1−3]。2012 年,梅军等[4]通过在弹性薄膜上附着特定款式的硬质金属片构造暗声学超材料,在共振频率附近能很好地吸收声波;2019 年,Donda 等[5]通过构造迷宫结构的超表面实现了50 Hz 附近的极低频吸收;2021年,Dong 等[6]提出一种通过耗散和干涉杂化的超宽带通风屏障,能够在650∼2000 Hz 范围内有效阻挡90%以上的入射声能量;Liu 等[7]将各向异性的概念引入到三维折叠空间的系统中,提出了一种打开低频、宽频声子带隙的方法,并设计了既能隔声降噪,又能通风透气的三维声学超构笼子。
然而,尽管声人工结构在低频吸隔声领域展现了其优越的性能,但针对实际应用中的低频宽带噪声,往往需要对多个声人工结构单元进行组合以实现宽带隔声降噪的效果。而这样的组合结构通常较为复杂,传统的人工设计方法高度依赖于设计者的专业知识和设计经验,设计效率较低。因此,研究者们开始期望寻求以目标声学响应为导向的自动化设计方法。早期的研究中,遗传算法(Genetic algorithm,GA)、粒子群算法等优化算法被普遍应用于解决声人工结构的逆设计问题[8]。但是,上述优化过程仍然需要大量的仿真模拟和参数迭代,计算成本依然很高。近年来,以人工神经网络为代表的深度学习(Deep learning,DL)在包括计算机视觉[9]、自然语言处理[10]、语声识别[11]、知识图谱[12]等计算机科学及工程领域取得了突破性的进展,也以惊人的速度在材料科学[13]、化学[14]、凝聚态物理[15]等其他学科领域展示了其独特的优势。此外,机器学习方法已经成为光学结构设计和电磁学结构设计的一个全新手段[16−18]。与传统方法相比,机器学习可以通过数据驱动的方式从大量的数据中自动发现和学习有用的信息,具备自主学习、联想储存、高速寻优等优点。
在之前的工作中,作者团队基于DL 模型实现了二阶亥姆霍兹共鸣器(Two-order Helmholtz Resonator,THR)单元的精准设计,并通过数值仿真和实验的方式验证了其对于线谱噪声降噪的有效性[19],但该模型无法直接应用到低频宽带噪声问题的解决上。因此,本文首先针对低频宽频隔声装置设计中普遍存在的耦合效应进行了仿真和分析,研究了影响耦合效应强弱的变量和因素;然后在上述工作的基础上提出了一种基于DL 的低频宽带隔声装置的设计方法,并基于该方法设计了一组包含9个THR 单元的组合结构,实现了158∼522 Hz 范围内的宽带隔声。
1 THR的理论模型
传统的亥姆霍兹共鸣器由一个短管和一个腔体串联而成,因此也被称为一阶亥姆霍兹共鸣器。该结构往往只具有一个共振频率,共振峰的宽度也较窄,在某些场景下应用会受到一定的限制。因此,人们开始对高阶亥姆霍兹共鸣器展开研究[20−21],并将其作为管道的旁支结构用于管路的隔声降噪。图1(a)为THR 作为管道旁支结构的结构示意图,灰色虚线框中的部分为一个THR单元。THR 包含两个短管和两个腔体,可以视作由两个一阶亥姆霍兹共鸣器串联而成。其中,a1和l1分别为一阶短管的半径和长度;r1和h1分别为一阶腔体的半径和长度;a2和l2分别为二阶短管的半径和长度;r2和h2分别为二阶腔体的半径和长度。因此,THR 的几何结构可以由几何参数gp=[a1,l1,r1,h1,a2,l2,r2,h2]来进行描述。
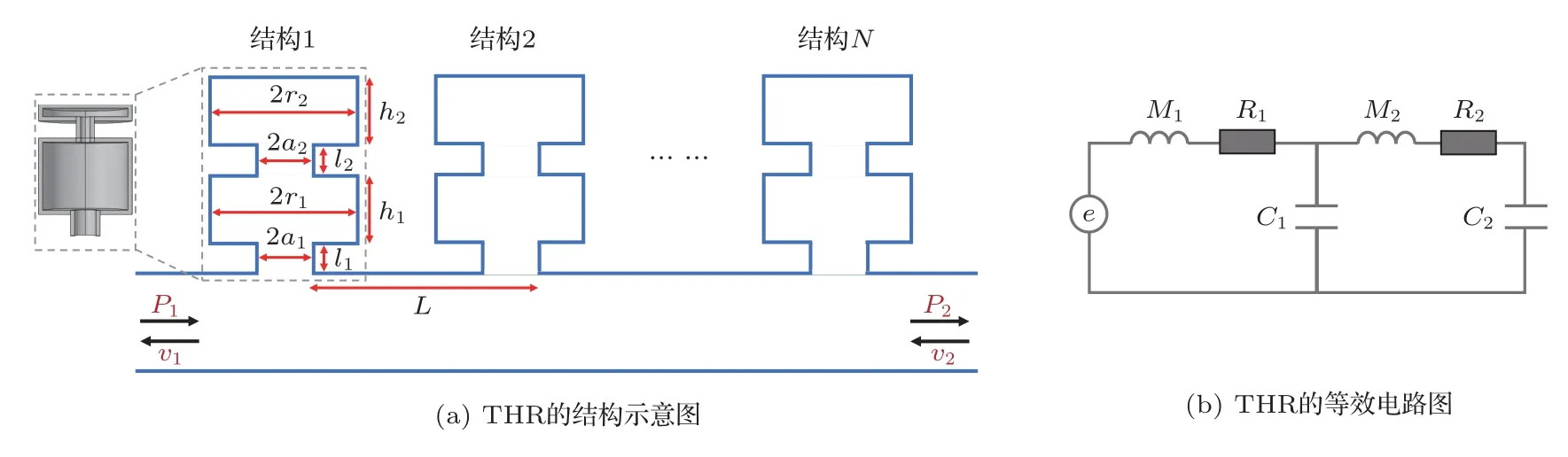
图1 THR 的结构示意图和等效电路图Fig.1 Schematic view and equivalent circuit diagram of the THR
在低频范围内,集总参数模型常被用于对THR进行建模和分析。图1(b)为THR的等效电路图,这里将短管等效为声阻R和声质量M,将腔体等效为声容C。因此,在集总参数模型下THR 可以由电学参数eep=[R1,M1,C1,R2,M2,C2]进行描述,几何参数gp 和电学参数eep 之间的转换关系如表1所示。其中,ρ0和c0分别为空气的密度和声速;η为空气的黏滞系数为第i阶短管的末端修正,修正因子β1=0.75,β2=1.05。利用集总参数模型可以求得该结构的声阻抗ZTHR为

表1 几何参数和等效电学参数的转换关系Table 1 Relationships between gp and eep
其中,ω=2πf为角频率。而此时带有旁支结构的管路的声传输损失(Sound transmission loss,STL)可以被表示为
其中,Rb和Xb分别为声阻抗ZTHR的实部和虚部;Z0=ρ0c0为空气的特性阻抗;S为管道的横截面积。通过分析公式(2)可知,当声阻抗ZTHR的虚部Xb=0时,STL为极大值点,降噪效果最好,此时对应的频率即为THR 的共振频率。一个THR单元通常有两个共振频率,分别对应STL 谱线中的两个共振峰。
2 基于THR的宽频隔声器件设计
2.1 单元间的耦合效应
虽然与一阶亥姆霍兹共鸣器相比,THR在不增加额外体积的基础上又引入了额外的高阶共振频率,但是单独的一个THR依然只能针对共振峰附近频带内的噪声进行降噪。因此,对于宽带噪声常常需要对多个THR 进行组合,以实现低频宽带隔声。多个THR 单元通常如图1(a)所示作为管道的旁支结构依次排列,其中THR 单元间的间隔为L。为了使隔声装置更加紧凑,相邻的单元间的距离一般比较小,所以单元间会存在一定的耦合效应。
为了更加形象地展现单元间的这种耦合效应,下面以3 个THR 单元的不同组合方式为例展开分析。为了方便叙述,这3 个THR 单元分别被编号为1号、2号和3号,对应的几何参数如表2所示。同时,本文也借助有限元方法(Finite element method,FEM)对这3 个THR 单元单独作为管道旁支结构时的STL谱线进行了计算。考虑到细管中的黏滞常常较大,因此仿真中对THR 单元的一阶短管和二阶短管区域的物理场设置为热黏性声学。计算结果如图2(a)所示,这里的黄色虚线为1 号单元的STL谱线,其共振峰分别出现在251 Hz 和430 Hz;绿色点线为2 号单元的STL 谱线,其共振峰分别出现在245 Hz和454 Hz;红色点划线为3 号单元的STL 谱线,其共振峰分别出现在275 Hz和504 Hz。这3个单元单独作为管道旁支结构时的共振频率同时也记录在表2的最后两行。

表2 3 个THR 单元的几何参数及共振频率Table 2 Geometric parameters and resonance frequencies of the three THRs
然后,将这3 个单元以图1(a)的形式,从左到右按照1 号结构、2 号结构和3 号结构的顺序依次排列,间距为20 cm,基于FEM 计算了该组合结构的STL 频谱,如图2(a)中蓝色实线所示。可以看到,该组合结构的STL具有6个共振峰,分别出现在245 Hz、251 Hz、275 Hz、431 Hz、454 Hz、504 Hz,高度均在30 dB 以上。与每个单元单独作为旁支结构相比,组合后结构的共振频率基本和每个单元的共振频率吻合,这说明在这种排列方式下耦合效应基本不会造成共振频率的偏移。同时,由于耦合效应的存在,组合结构共振频率附近的STL 有了较为明显的提升,其最终的隔声效果并不是每个单元隔声量的简单叠加。
其次,改变了组合结构单元之间的间距L,基于FEM 计算了不同单元间距的组合结构的STL频谱,如图2(b)所示。其中,蓝色实线为间距L=15 cm 时组合结构的STL 频谱,黄色虚线为间距L=20 cm 时组合结构的STL 频谱,绿色点线为间距L=25 cm 时组合结构的STL 频谱。观察图2(b)的3 条曲线可知,改变单元之间的间距依然不会造成共振频率的明显偏移,但是会对共振频率附近的STL造成一定的影响。
最后,还探究了单元顺序对组合结构STL 谱线的影响。改变了3 个单元的相对位置,同时固定单元间距L=20 cm不变,基于FEM计算了不同顺序下组合结构的STL谱线,如图2(c)所示。其中,蓝色实线为将3 个单元按照1 号、2 号和3 号的顺序依次排列后的组合结构(以下简称“1-2-3”组合)的STL谱线;黄色虚线为将3 个单元按照1 号、3 号和2 号的顺序依次排列后的组合结构(以下简称“1-3-2”组合)的STL 谱线;绿色点线为将3 个单元按照2 号、1 号和3 号的顺序依次排列后的组合结构(以下简称“2-1-3”组合)的STL 谱线。对比“1-3-2”组合的STL 谱线和另外两条谱线,可以看到“1-3-2” 组合的STL 谱线在251 Hz 处的共振峰的高度明显低于另外两条谱线。该共振峰为1 号单元的一阶共振峰,且与2 号单元的一阶共振峰在频率上较为接近。而在“1-3-2”组合中,1 号单元和2 号单元间放置了一个3 号单元,导致两个单元相距较远,因此这两个共振峰间的耦合效应被削弱了,致使“1-3-2”组合在251 Hz处的共振峰的高度更接近于1号单元原本的一阶共振峰的高度,并没有因为耦合效应的存在有所提升。类似的效应也存在于“2-1-3”组合第五个共振峰和第六个共振峰的中间区域,在这个频带内“2-1-3”组合的STL 谱线较另外两条谱线相比出现了很明显低谷。这其实是因为组合中2 号单元和3号单元距离较远,因此2 号单元的二阶共振峰和3号单元的二阶共振峰间的耦合效应被虚弱了,导致组合结构在该频率区间的STL较低。
综上所述,由于耦合效应的存在,对组合结构中的单元进行独立设计并不是最优的选择。应该在对组合结构设计的过程中充分考虑单元间的耦合效应,并对其加以利用。例如,可以将共振频率相近的单元尽可能放置在相邻的位置处,以达到提升组合结构隔声效果的目的。
2.2 基于DL的THR设计
由2.1 节的分析可知,在设计宽带隔声装置的过程中应该充分考虑并利用单元间的耦合效应,对整个组合装置进行一体化设计,而不是对每个单元独立设计后再进行组合。这里为了简化问题,固定腔体半径r1=r2=5 cm。因此,每个单元均包含6个待调节的几何参数[a1,l1,h1,a2,l2,h2],这些几何参数都会影响组合结构的隔声性能。一个宽带隔声装置往往由多个THR 单元组成,传统的基于人工设计的方法需要依赖设计者的经验去手动调节这些参数以达到期望的性能,设计效率很低,因此并不适用于设计包含多个待调节参数的复杂结构。
在之前的工作中,作者团队基于DL 模型建立了期望的STL 频谱和THR 单元的等效电学参数之间的映射关系,实现了声学结构的自动化的精准设计[19]。首先,基于集总参数模型正向生成了约19.5×104条样本数据,经过一定筛选后被划分为训练集、验证集和测试集。随后。基于pytorch 框架搭建了一个5 层全连接神经网络,网络的输入为从101∼600 Hz 间隔为1 Hz 的STL 谱线,输出为6维的等效电学参数,隐含层的神经元个数分别为450、250 和220。模型训练时所使用的损失函数为均方误差函数(Mean square error,MSE),学习率为0.001,批大小(Batch size)为256。同时,为了缩短训练时间,防止过拟合,在训练过程中采用了批标准化(Batch normalization)和Dropout 等策略。经过约200 个epoch 的训练后模型逐渐收敛,最终所得到的模型在测试集上的平均损失为0.0029。
在使用所得到的DL 模型对THR 单元进行设计时,首先需要根据目标隔声频率生成期望的STL频谱,并将其输入到DL 模型中;然后模型会根据输入的STL 频谱输出预测的等效电学参数;最后可以根据表1 中的等效电学参数和几何参数的转化关系,计算出对应的几何参数,构建相应的THR单元,并通过数值仿真等手段验证该结构的隔声性能是否符合预期目标。
为了进一步展现所提出的基于DL 的设计方法在计算效率上的优越性,将其与声学结构设计领域较为常用的GA 进行了对比,分别基于这两种方法对在目标隔声频率处STL 大于10 dB 的THR 单元进行了设计。所使用的GA 是基于开源工具箱Geatpy 中的soea_SEGA 所实现的,初始种群规模为100,所采用的适应度函数F为
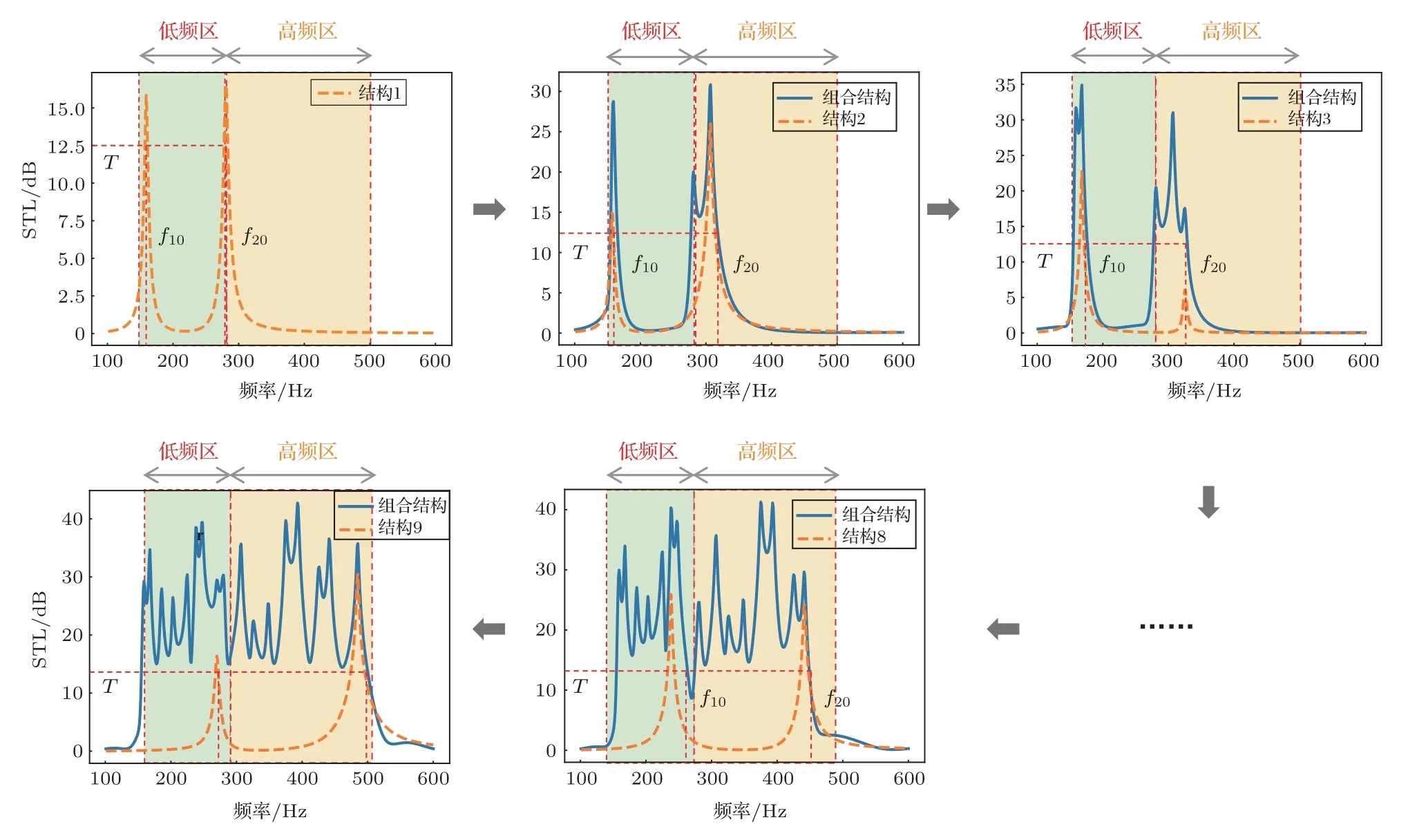
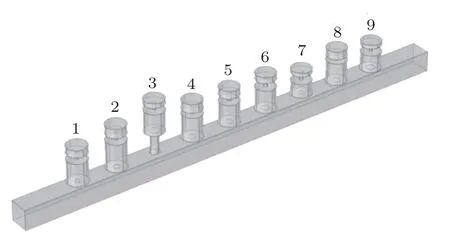
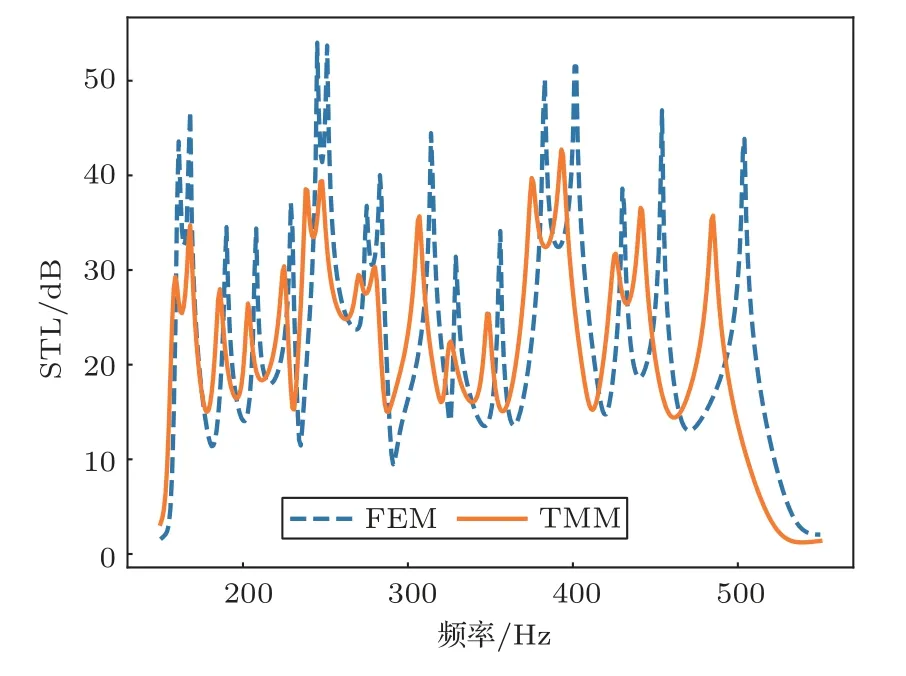
其中,f1和f2分别为结构的一阶共振频率和二阶共振频率。λ的引入可以在很大程度上引导结构的共振频率向方向进化,从而更快地达到期望的设计目标。使用上述适应度函数对THR单元的6 个待定几何参数[a1,l1,h1,a2,l2,h2]进行寻优,考虑到结构的可加工性,几何参数调节范围被设置为0.1 cm 这里选取了3 组目标隔声频率,并且为了不失一般性,针对每组设计目标都分别基于DL 和GA进行了20 次求解并记录了每次求解所用的时间,如图3 所示。第1 组目标频率为,基于DL 的20 次设计的平均耗时为8.7 s,基于GA 的20 次设计的平均耗时为27.5 s。第2 组目标频率为,基于DL 的20 次设计的平均耗时为2.5 s,基于GA 的20 次设计的平均耗时为43.1 s;第3 组目标频率为和,基于DL 的20 次设计的平均耗时为4.4 s,基于GA的20次设计的平均耗时为55.3 s。从上述3 个对比实验的最终计算结果中各选取了一组THR 单元,并基于传输矩阵法(Transfer matrix method,TMM)计算了结构对应的STL 谱线,如图4 所示。可以看到,通过这两种方式设计得到的THR单元在性能方面并无明显的差异,都与预期目标吻合得很好。因此,与传统的优化类算法相比,所提出的基于DL 的设计方法具有更高的计算效率,模型一旦训练完成,可以在很短的时间内设计出满足需求的THR 单元,这为实现低频宽带隔声装置的设计提供了很大的便利。 图3 DL 与GA 的设计效率对比Fig.3 Comparison of the computational efficiency of DL and GA 图4 针对3 个不同的优化目标的优化结果对比Fig.4 Comparison of the optimization results for three different optimization objectives 这里基于DL 模型提出了一种用于低频宽带隔声的组合结构的设计方法,设计过程如图5 所示。将有隔声需求的频带区域划分为低频区和高频区,同时确定一个隔声指标T。在设计过程中,需要依次对每个THR 单元的几何参数进行设计,最终目标是利用所有THR 单元的一阶共振峰使低频区的STL 均大于T,同时利用THR 单元的二阶共振峰使高频区的STL均大于T。在对第i个THR单元进行设计时,首先需要基于前i−1 个THR 单元所组成的组合结构的STL 频谱分别找到低频区和高频区STL 小于T的最低的频点(分别记作f10和f20),然后基于DL 模型生成N个共振频率分别在f10和f20附近的结构。考虑到单元间的耦合效应,需要将这N个结构分别与前i−1 个THR 单元进行组合,计算组合结构的STL,并以此来筛选出最优的结构作为第i个THR单元。图5 每幅子图中的黄色虚线代表第i个THR单元的STL谱线,蓝色实线则为前i个单元组合后的组合结构的STL 谱线。不断重复上述过程,直至低频区和高频区所有频点的STL 均大于T。 图5 低频宽带隔声装置的设计过程Fig.5 Design process of the low-frequency broadband sound insulation device 由于低频区域的一阶共振峰往往较为尖锐,高度也较低,在设计过程中低频部分的设计进度往往是落后于高频部分的,可能会出现高频区的所有频点的隔声量都达标了,但是低频区仍有频点隔声量不达标。为了避免这种情况的发生,可以在划分低频区时适当增大高频区的带宽,减少低频区的带宽;此外,在制定打分标准时也可以对低频区域和高频区域分开进行打分,并赋予低频部分更高的权重,使得在挑选结构时优先考虑该结构对低频区隔声量的提升效果。 基于上述方法,设计了如图6 所示的宽频隔声装置,共包含了9 个THR 单元,每个单元的间隔为20 cm。考虑到基于FEM 对组合结构进行计算时,随着单元个数的增加计算成本会越来越高,因此,为了降低设计过程的计算成本,提高设计效率,使用TMM对设计过程中产生的组合结构的STL频谱进行计算。由于TMM 对结构进行建模时引入了一些近似,基于TMM 计算得到的共振频率可能会低于结构真实的共振频率,从而导致结构真实的STL 频谱中相邻共振峰之间的间距比预期的更大,共振峰间频带的STL低于预期目标。考虑到上述误差的影响,在设计过程中可以适当提高传输损失的设计目标T,以缩小相邻共振峰的间距,避免共振峰间出现无法接受的低谷。 图6 低频宽带隔声装置示意图Fig.6 Schematic view of the low-frequency broadband sound insulation device 最终得到的宽频隔声装置中各个THR 单元的几何参数如表3 所示,组合结构的STL 频谱如图7所示。黄色实线为基于TMM 的计算结果,蓝色虚线为基于FEM的计算结果。结果表明,该组合结构的隔声频段为158∼522 Hz,达到了低频宽带隔声10 dB 以上的预期目标。正如之前所分析的,基于FEM 的结果和基于TMM 的结果之间存在一定的差异,且这种差异性在高频更加明显。但是,二者所呈现出的大体趋势是一致的,且TMM 的计算复杂度更低,因此在设计宽频器件的过程中使用TMM可以大大提升设计效率,也可以满足宽频隔声的设计目标。 图7 宽频隔声装置的STL 谱线Fig.7 STL spectrum of the low-frequency broadband sound insulation device 表3 宽频隔声装置各个THR 单元的几何参数Table 3 Geometric parameters of the THRs 由于单个THR 单元的工作频带往往较窄,在实际应用中常常需要对多个THR 单元进行组合以实现低频隔声降噪的目的。这种组合结构通常包含多个待调节的参数,传统的设计方法设计效率往往很低。因此,本文提出了一种基于DL 的低频宽带隔声装置的设计方法,实现了对包含多个THR 单元的隔声装置的快速自动化设计。本文基于集总参数模型完成了对THR 单元的理论建模,同时对组合结构中单元间的耦合效应进行了分析,为低频宽带隔声装置的设计提供了理论基础;简要介绍了基于DL 模型的THR 单元的设计方法,并将其拓展到了低频宽带隔声的组合结构设计中;采用所提出的方法对包含9 个亥姆霍兹共鸣器单元的组合结构进行了设计,实现了158∼522 Hz范围内的宽带隔声,并基于TMM 理论和FEM 理论验证了该设计的有效性。和传统的人工设计相比,基于DL的设计方法可以通过数据驱动的方式从大量的数据中自动发现和学习有用的信息,减少对设计者专业知识和设计经验的依赖,是声学结构按需设计和优化的有效工具。考虑到集总参数模型可以在低频范围内准确地分析各种声学结构,该方法具有很强的通用性和可扩展性,未来也可以进一步向其他声学结构设计领域进行推广。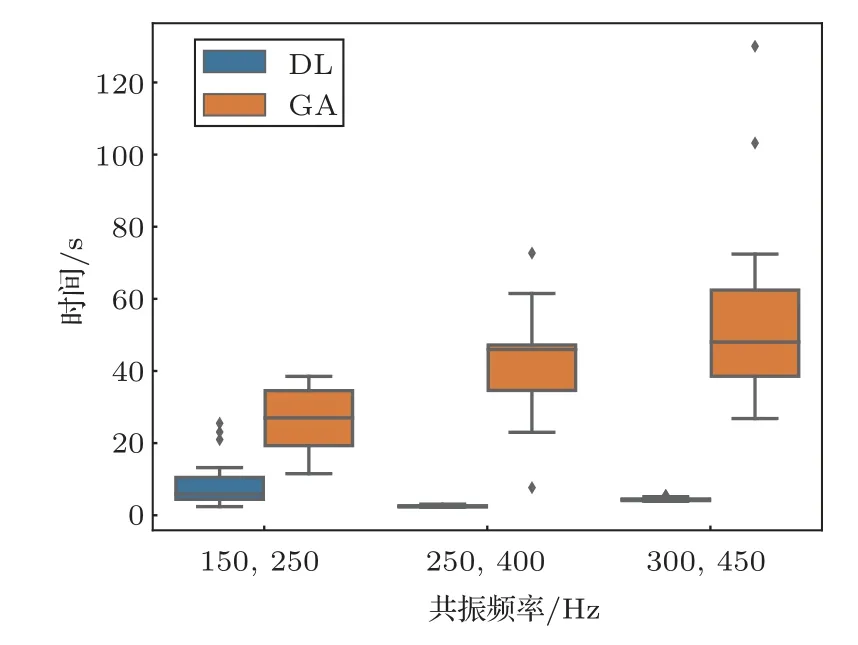

2.3 基于DL的低频宽带隔声装置的设计方法

3 结论

