质点沿对数螺线运动的速度和加速度
陈 彦, 王 威
(扬州职业大学, 江苏 扬州 225009)
《理论力学》中运动学部分关于点的变速曲线运动给出了点的速度、切向加速度、法向加速度和全加速度的一般计算公式[1],但经典的例子不是很多,只有一道摆线(或旋轮线)和一道阿基米德螺线的例题。由于变速曲线运动本身的复杂性,所以必须和一般曲线的几何性质结合起来加以研究。对数螺线是质点切向、法向加速度均为常数的平面运动轨迹[2-3]。质点能不能以等角速度绕固定点转动的同时又沿着对数螺线运动?邵云以匀速转动的水平光滑直管内小球的离心运动为例给出了肯定的答案[4],但是并没有给出质点速度和加速度的一般计算公式,也没有清楚地阐明质点分别在自然轴系、极坐标系和动参考系中速度矢量和加速度矢量的内在统一性以及和对数螺线的几何性质有何关联,笔者针对这些问题进行分析讨论。
1 质点沿对数螺线运动的速度与加速度公式
对数螺线在极坐标系(ρ,θ)下的一般方程为:
ρ=aebθ(a>0,b≠0)
(1)
它的图形如图1所示,从起点A(ρ=a,θ=0)出发,逆时针转向,随着极角的增大,当b>0时,越绕越远离极点;当b<0时,越绕越靠近极点而永远达不到极点。对数螺线最重要的几何性质就是等角性,即曲线上任意一点的切矢与径矢成固定角度α=arccot(b)(0<α<π,α≠π/2),α为对数螺线的倾斜度,所以对数螺线又叫等角螺线。
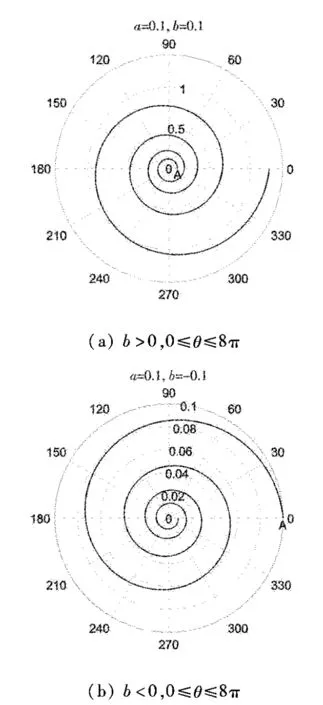
图1 对数螺线
1.1 质点沿对数螺线运动的速度
将对数螺线在极坐标系下的方程转化为直角坐标系下以θ为参数的参数方程[5]如下:
(2)
如果质点从起点A(ρ=a,θ=0)开始绕极点等角速度转动,并且沿着对数螺线运动,设角速度为ω,以逆时针转动为正,顺时针转动为负,从而θ=ωt,先将其代入方程(1),得到极径ρ与时间t的关系式(3),再代入方程(2),转化为以时间t为参数的参数方程(4),如下:
ρ(t)=aebωt(a>0,b≠0,t>0)
(3)
(4)
已知参数方程形式的弧微分公式[5]如下:
(5)
将方程(4)代入式(5)并化简得
(6)
这样质点在任意时刻的线速度为:
(7)
τ为切向单位矢量,指向与质点的运动方向一致,根据教材,公式有[6]
(8)
将方程(4)代入式(8)并化简得:
τ=(cos(ωt+arccotb),sin(ωt+arccotb) )
=(cos(ωt+α),sin(ωt+α) )
(9)
根据《理论力学》中速度在极坐标系中的投影式,将方程(3)与θ=ωt代入,计算结果如下:
(10)
1.2 质点沿对数螺线运动的加速度
通过公式(6),求得质点在任意时刻沿对数螺线运动的切向加速度为:
(11)
从速度(7)和切向加速度(11)的表达式可以看出,当bω>0时,二者符号相同,质点作变加速曲线运动(图2(a));当bω<0时,二者符号相反,质点作变减速曲线运动(图2(b))。
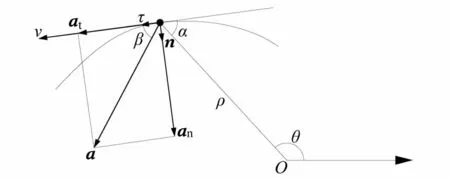
(a)变加速曲线运动(α=β,ω>0,b>0)
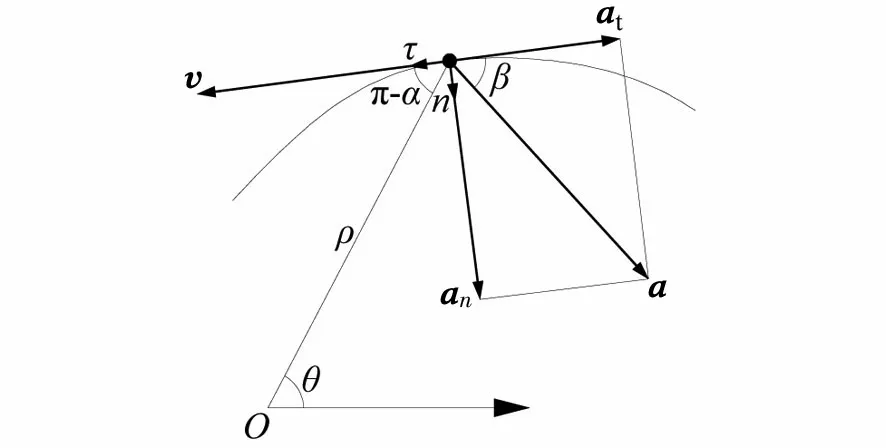
(b)变减速曲线运动(π-α=β,ω>0,b<0)图2 质点沿对数螺线运动
已知参数方程形式的曲率公式如下:
(12)
将方程(4)代入式(12),求出质点在任意时刻所在位置的曲率,并化简得
(13)
从而求得质点在任意时刻沿对数螺线运动的法向加速度为
(14)
n为法向单位矢量,如图2所示,指向曲线内凹一侧,可由τ旋转90°得到
n=(-sin(ωt+α),cos(ωt+α))(ω>0)
n=(sin(ωt+α),-cos(ωt+α))(ω<0)
(15)
所以全加速度大小
(16)
如图2所示,它与切向加速度之间的夹角的余切为
(17)
所以β=arccot|b|(0<β<π/2),此角度恰好等于对数螺线的倾斜度或其补角,结合对数螺线的等角性得出结论:全加速度的方向恰为径矢方向或者与之关于内法线轴对称的方向。
根据《理论力学》中加速度在极坐标系中的投影式,将方程(3)与θ=ωt代入,计算结果如下:
(18)
容易验证
(19)
aρ即为全加速度在径矢方向的投影,因为a、b和ω都不等于0,所以aθ肯定不为0,也就是全加速度在θ方向必然有分量。假设质点沿着对数螺线逆时针转动(ω>0),不管作变加速运动(b>0)还是作变减速运动(b<0),全加速度的方向一定是沿着与径矢关于内法线轴对称的方向,且指向曲线内凹一侧,如图2所示;而顺时针转动(ω<0)的情况正好相反。
2 应用实例
如图3所示,内壁光滑的直管在水平面内绕其端点O以匀角速度ω转动,设初始时刻t=0,此时直管位于Ox轴,质量为m的小球相对静止于管内A点,OA=k。随着直管的转动,小球在离心力的作用下被甩出。
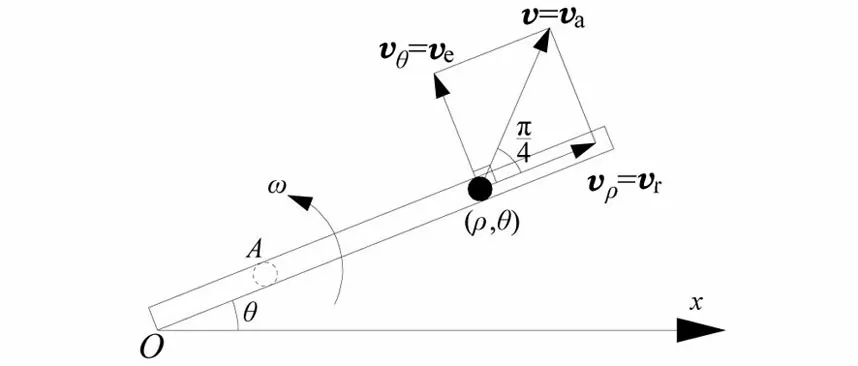
(a)小球的速度
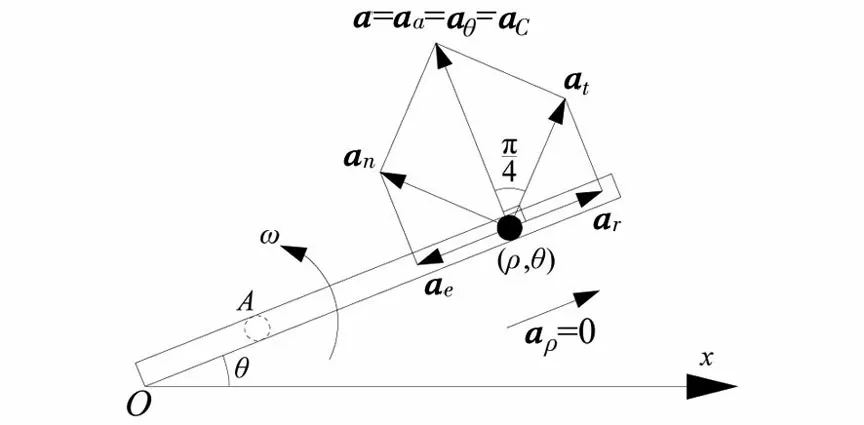
(b)小球的加速度图3 匀速转动光滑直管内小球的离心运动
设t时刻小球的极坐标为(ρ,θ),如果以地面为定参考系,小球的绝对速度为va,绝对加速度即全加速度为aa;如果以转动的直管为动参考系,小球的相对速度为vr,相对加速度为ar。牵连点为A点,牵连速度为ve,牵连加速度为ae,由于牵连运动为定轴转动,所以小球存在科氏加速度aC。根据文献[4]中的结论,在直管旋转半圈后,即θ>π时,小球的运动轨迹近似为对数螺线,此时小球的运动轨迹方程为:
(20)
对比方程(3),显然a=k/2,b=1,所以此对数螺线的倾斜度α=π/4。
2.1 小球的速度
在定参考系中分析小球在t时刻的速度,将a和b代入式(7),得小球的线速度即绝对速度:
(21)
其中τ=(cos(ωt+π/4),sin(ωt+π/4)),从图3(a)中可以看出小球的速度方向与直管径向的夹角即为此对数螺线的倾斜度。
在转动参考系中分析小球的速度,将a和b代入式(10),并且小球的相对速度vr和牵连速度ve的大小与速度在极坐标系中的投影满足
(22)
所以小球的相对速度vr刚好等于速度在极坐标系中的径向分量vρ,而牵连速度ve刚好等于速度在极坐标系中的环向分量vθ,方向如图3(a)所示,结论和文献[4]一致。
如果从不同参考系的角度理解速度矢量的合成,即
v=va=vρ+vθ=vr+ve
(23)
2.2 小球的加速度
在定参考系中用自然轴系分析小球在t时刻的加速度,将a和b分别代入式(11)、式(14)和式(16),得小球切向加速度at和法向加速度an的大小:
(24)
方向如图3(b)所示,得小球全加速度a的大小即绝对加速度aa的大小:
a=aa=kω2eωt=2ρ(t)ω2
(25)
根据上面的结论得知全加速度方向与速度方向夹角也等于π/4,由于小球作变加速运动,如图3(b)所示全加速度方向必然与直管垂直,指向极角增大的地方。
在转动参考系中分析小球的加速度,将a和b代入式(18),得aρ=0,从式(18)中可以看出加速度的径向分量aρ中的第一项即相对加速度ar,第二项即牵连加速度ae,二者大小相等,方向相反,如图3(b)所示,即
ar=ae=ρ(t)ω2
(26)
而式(18)中的环向分量aθ即为小球的科氏加速度aC,所以
aθ=aC=kω2eωt=2ωvr=2ρ(t)ω2
(27)
方向如图3(b)所示,结论和文献[4]一致。
如果从不同参考系的角度理解加速度矢量的合成,即
a=aa=at+an=aρ+aθ=ar+ae+aC
=aθ=aC
(28)
3 结语
对数螺线最重要的几何性质就是等角性,结论刚好验证了这一性质。可见在一般曲线运动中,质点的切向和法向加速度均为常数这个条件,只是运动轨迹为对数螺线的充分但非必要条件。以匀速转动的水平光滑直管内小球的离心运动为例,运用本文的计算公式,验证了文献[4]结论的正确性,并且清楚地阐明了质点分别在自然轴系、极坐标系和动参考系中速度矢量和加速度矢量的内在统一性。
——兼谈参考系与坐标系的关联关系

