弹载雷达阵列幅相误差校正及目标超分辨技术

胡衍墨,邓维波,刘爱华,张 鑫

(1.哈尔滨工业大学电子与信息工程学院,黑龙江 哈尔滨 150001;2.上海无线电设备研究所,上海 201109)

0 引言

主瓣内多目标分辨一直以来都是阵列信号处理的研究重点,在雷达抗干扰[1]、目标识别等领域有着极大的应用潜力。然而,采用传统的阵列信号处理方法进行波束测角,分辨空间中的两个目标时,分辨能力严重依赖雷达的波束宽度,不能分辨一个波束内的两个目标,即存在瑞利限[2-3]。

为提升角度分辨能力,已有多种超分辨算法被提出,例如多重信号分类(MUSIC)算法[2]、旋转不变子空间(ESPRIT)算法[4]、基于压缩感知(CS)的角度超分辨算法[5]等。出于稳定性和计算量的考虑,本文采用平滑MUSIC 算法处理主瓣内的相干目标回波信号,突破瑞利限,以提升角度分辨能力。特别地,对主瓣内存在两个目标的特殊情况进行分析,给出双目标情况下的二维面阵平滑方法,并分析该方法的计算复杂度。

此外,不同通道间存在的幅相误差以及天线耦合效应[6]等会对空间测角产生一定影响,因此需要进行通道补偿。本文采用先进的补偿技术,利用波达方向(DOA)估计中的信号矩阵特性修正阵列的幅相误差[7],并利用强回波信号进行幅相误差校正,恢复空间角度的估计精度和分辨能力。

1 二维平面阵信号模型

二维平面阵列示意如图1所示。建立以阵元中心o为原点的直角坐标系oxyz,设平面阵列的阵元数为MN,阵元间隔均为半波长。阵元位置矩阵(T 为矩阵转置运算符),其中阵元(m,n)的位置矢量dm,n=[xm,yn]T,xm和yn分别代表阵元(m,n)在x轴和y轴上的位置坐标,m=1,2,…,M,n=1,2,…,N。φ和θ分别为目标点P相对于阵列中心o的俯仰角和方位角。

图1 二维平面阵列示意图

假设空间共存在K个信号源,方向分别为(φ1,θ1),(φ2,θ2),…,(φk,θk),…,(φK,θK),设u（φk,θk）=[sinθkcosφk,cosθkcosφk]T为第k个信号的空间二维方向矢量,则第k个信号从阵元(m,n)到阵元(1,1)的延迟可以表示为

式中:c为光速。阵元(m,n)上的信号可以表示为

式中:gm,n为阵元(m,n)的幅相误差;sk(t)为第k个回波信号;Nm,n(t)为阵元(m,n)上的噪声。一般地,将阵元(1,1)作为参考阵元,有g1,1=1。将式 (2)写为矩阵形式,有

式中:diag(·)为生成对角矩阵函数;ω=2π/λ为波数,λ为信号波长。假设阵列共获取了L个快拍,此时式 (3)可以写成矩阵形式

式中:X∈CMN×L为接收信号矩阵,C为复数集;G=diag（g）∈CMN×MN为幅相误差矩阵,其中g=[g1,1,g1,2,…,gM,N]T∈CMN×1为幅相误差矢量;A∈CMN×K为阵列流型矩阵;S∈CK×L为目标的回波信号矩阵;N∈CMN×L为噪声矩阵。

阵列流型矩阵A也可以使用阵列导向矢量获得,即

其中

式中:a(φk,θk)为阵列导向矢量。

2 利用强回波信号的幅相误差校正

本文利用已知来波角度的强回波信号校正阵列的幅相误差。假设该信号来波的俯仰角和方位角为φc,θc,则式 (4)可以改写为

式中:Xc∈CMN×L为阵列的L次快拍的信号;a(φc,θc)∈CMN×1为已知来波信号的阵列导向矢量;sc∈C1×L为强回波信号。

为了估计幅相误差矩阵G,首先构造信号Xc的协方差估计矩阵

式中:H 为矩阵共轭转置运算符。将式(7)代入式(8)中,理论上,在L→∞的情况下,可以得到

式中:σ2s为强回波信号功率;σ2n为噪声信号功率;IMN×MN为MN×MN的单位阵。

随后,对进行特征分解。将除最大特征值外的其余特征值对应的特征向量构成的矩阵记为∈CMN×(MN-1),则满足

估计幅相误差g需要求解

式中:min(·)为取最小值函数;‖·‖2为2范数运算符。

式 (11)的等价形式为

其中

此时,根据式 (12),式 (11)可以写为

对式(13)求导并约束结果为0,得到

则的估计矩阵

式中:-1为矩阵求逆运算符。综上,可以得到幅相误差的估计

随后,对式 (7)进行校正,校正后的接收信号矩阵

3 空间平滑MUSIC算法

传统的MUSIC算法在信号具有一定相干性的情况下是失效的。这是因为在空间存在K个信号源时,信号协方差矩阵的秩不为K,会对空间谱估计产生严重影响。因此需要使用平滑MUSIC算法将信号的秩重新恢复为K,得到空间目标的具体角度。本文以K=2的情况为例,说明面阵的平滑处理方法。

3.1 平滑方法

本文使用4次平滑的MUSIC 算法实现相干信号的DOA 估计。在MN×MN等间距排列的平面阵中选取4个子阵,每个子阵有Q个单元。

使用矩形平滑方法处理相干信号,二维平滑示意如图2所示。

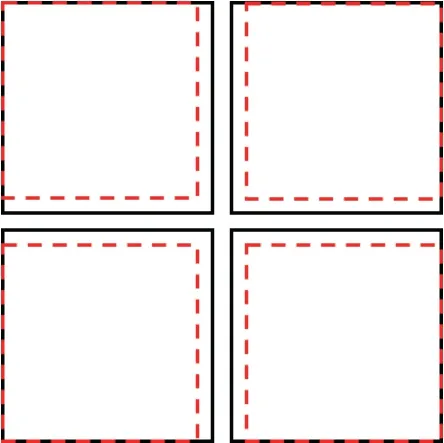
图2 二维空间平滑示意图

图2中4个实线框均代表MN×MN的二维平面阵,其中的4个虚线框代表4个子阵,即利用这4个子阵进行平滑。4个子阵的位置分别为:(1～M-1)×(1～N-1),(1～M-1)×(2～N),(2～M)×(1～N-1),(2～M)×(2～N)。为了简化后续的模型推导过程,分别假设上述4个子阵阵元位置的索引值为ρ1,ρ2,ρ3和ρ4,同时可得Q=(M-1)(N-1)。这种位置选择方法既保留了矩形平面阵的特性,又最大化地减少了阵列自由度和估计精度的损失,因此本文采用这种方式进行空间平滑。

3.2 算法推导

定义第l个平滑子阵的信号矩阵[8]

其中

式中:Ab∈CQ×K为第一个子阵的阵列流型,其列为Q维的导向矢量;Nl为第l个平滑子阵的噪声矩阵。第l个平滑子阵的协方差矩阵

式中:RS为信号协方差矩阵。将这4个平滑协方差矩阵做平均,则前向平滑协方差矩阵

相干回波的空间平滑算法虽然可以恢复协方差矩阵的秩,即rank(Rf)=K,但相对于原阵列,阵列的有效孔径减小了,进而损失了一定自由度。

对Rf进行特征分解,并将特征值由大到小排列,由后N-K个特征值对应的特征向量构成的噪声空间记为。随后利用二维MUSIC 算法进行极大值搜索,MUSIC谱峰搜索函数

下面计算该算法的复杂度。MUSIC 算法通过空间二维搜索进行角度估计。设空间角度的估计精度为δ,由于是空间二维搜索;设MUSIC 算法的网格划分数n=(180°/δ)2,则算法的复杂度

4 仿真分析

对14×14的空间二维平面阵进行仿真实验,阵元间的间隔均为半波长,分别研究本文算法对幅相误差的校正性能和主瓣内同时存在两个目标时的角度分辨能力。

4.1 利用强回波的幅相误差校正性能

假设幅相误差的幅度存在2 dB的变化,产生±10°的相位变化。在10 次快拍下评估本文算法,强回波的来波方向设为(0°,0°),每个阵元接收回波信号的信噪比设为40 dB。仿真实验中共有196个天线阵元,每个天线阵元的幅相误差均不同,196个天线阵元接收回波信号真实的幅度和相位以及利用本文算法得到的对应估计结果如图3所示。可见,不论是幅度还是相位,估计值均与真实值基本一致,说明了强回波下本文算法对幅相误差校正的有效性。

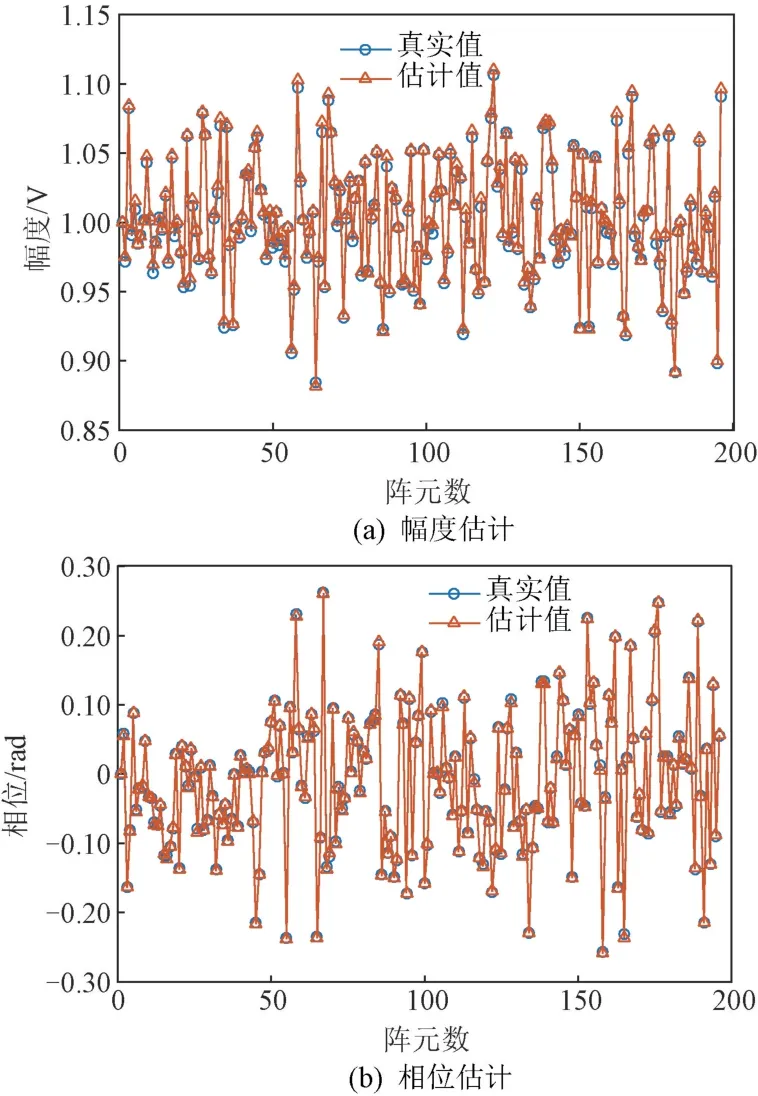
图3 信噪比为40 dB时幅相误差估计仿真结果

为了进一步说明本文算法的性能,设定快拍数为10,不同信噪比条件下幅相误差校正性能的仿真结果如图4 所示,图中利用均方根误差(RMSE)描述估计性能。可知:不同信噪比时幅度和相位的RMSE的数值相同;随着信噪比的提升,幅度和相位的RMSE均逐渐降低。

图4 不同信噪比时幅相误差校正仿真结果

设定天线阵元接收信号的信噪比为40 dB,不同快拍数下幅相误差校正的仿真结果如图5所示。

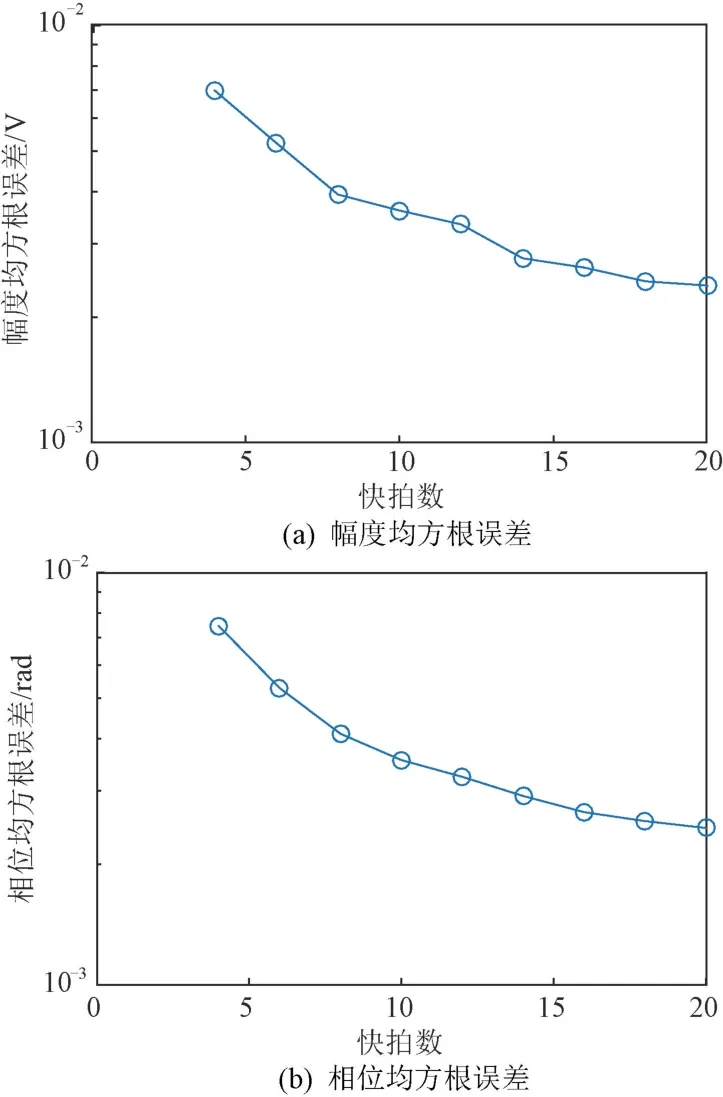
图5 不同快拍数时幅相误差校正仿真结果

由图5可知:随着快拍数的增加,幅相误差的校正更加精确;相比于小快拍数,在大快拍数下增加相同数量的快拍并不能显著提升估计精度。

总地来说,上述仿真实验结果说明了强回波下幅相误差校正的必要性。

4.2 不存在幅相误差时的超分辨性能

使用平滑MUSIC算法进行角度超分辨性能仿真。假设空间两个来波完全相关,来波方向分别为俯仰角θ1=20°、方位角φ1=20.0°,俯仰角θ2=22°、方位角φ2=21.5°。共进行4次平滑,平滑方法如图2所示。共取4个矩形子阵计算协方差矩阵,加权平均后得到平滑协方差矩阵。仿真中每个阵元接收信号的信噪比为35 d B。

基于平滑MUSIC 算法的目标分辨结果如图6所示。可见平滑MUSIC 算法可以区分两个邻近目标。经分析可知,在球坐标平面上两个目标的角度距离为2.5°,而此时阵列的3 dB波束宽度为9°,分辨率为波束宽度的0.28倍。而传统波束形成参数估计方法受限于阵列孔径的影响,无法突破瑞利限分辨位于阵列主瓣内的两个目标。

图6 二维空间平滑MUSIC算法目标分辨结果

4.3 存在幅相误差时的超分辨性能

为了说明幅相误差对超分辨算法性能的影响及幅相误差校正的有效性,利用图3所示仿真结果进行超分辨估计。

在不进行幅相误差校正的情况下,采用二维空间平滑MUSIC 算法分辨空间中的两个目标,仿真结果如图7所示。可知这种情况下不能成功分辨两个目标。在进行幅相误差校正后,采用该算法的目标分辨结果如图8所示。虽然两个峰值的高度不同,但完全可以成功分辨两个目标。这说明幅相误差对角度超分辨估计的影响较大,而且幅相误差校正是完全必要的,这同样说明了本文算法和估计流程的合理性和有效性。

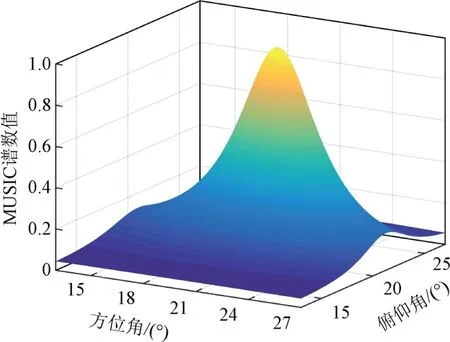
图7 未进行幅相误差校正的二维空间平滑MUSIC算法目标分辨结果

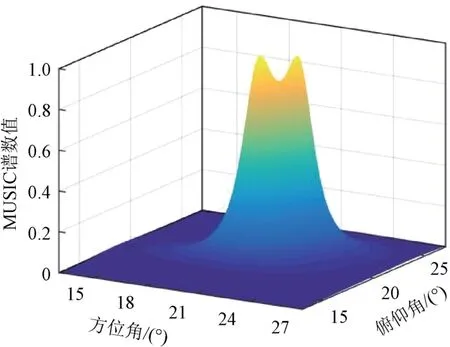
图8 幅相误差校正后二维空间平滑MUSIC算法目标分辨结果

5 结论

本文研究了存在幅相误差的情况下,使用二维面阵区分主瓣内两个目标的方法。利用强回波信号对阵列的幅相误差进行估计和补偿,并进一步采用平滑MUSIC算法实现角度超分辨。在幅相维,利用噪声子空间的正交性,采用凸优化方法估计幅相误差。在角度维,给出了面阵平滑处理方法,并计算了算法的复杂度。实验结果表明,本文算法可以有效估计阵元幅相误差,增加信噪比和快拍数有利于提升估计精度。在未进行幅相误差校正时,角度超分辨算法失效,不能有效分辨主瓣内的两个目标。但利用本文算法补偿幅相误差,可以恢复平滑MUSIC 算法的分辨能力。这说明幅相误差对角度超分辨估计的影响较大,需要进行校正,同时说明了本文算法、模型和处理流程的有效性。

本文所提幅相误差校正算法属于有源校正算法,需要预先明确强回波校正目标的具体方位。后续研究重点应集中在阵元幅相误差和目标角度的同时估计上。