基于网格搜索的被动单站旋转定位算法

陈 祎,蒲 彬,张晓丽,雷舒杰,段韵章

(上海无线电设备研究所,上海 201109)

0 引言

在现代电子战复杂的电磁环境中,目标参数信息获取是作战双方雷达系统需具备的核心功能。谁先获取了对方目标更多的参数信息,谁就拥有更大的决策权,也就获得了作战的主动权[1]。在实际应用中,目标定位是目标参数获取中研究最广、成果最为丰富的领域。目标定位可分为有源定位和无源定位。有源定位是依靠平台自身辐射的电磁波,通过处理目标反射回波获得目标位置信息;而无源定位则是通过直接处理目标辐射的电磁信号来解算目标位置信息。与有源定位相比,无源定位具有隐蔽性强、作用距离远、监视范围广、不易受干扰等突出优点,在电子侦察系统中得到了非常广泛的应用[2-5]。

无源定位方式包括多站无源定位和单站无源定位。常规的无源定位算法包括时差定位法、角度交叉定位法、相位差变化率定位法、频率变化率定位法等[6-7]。在工程应用中,多站无源定位会面临设备量大、站间时间同步要求高、站间数据通信需求大等问题,而单站无源定位不存在上述问题[8]。在现代军事电子系统强调隐蔽性和杀伤性的背景下,单站无源定位无疑具有更大的军事研究价值。而现有的单站无源定位算法均需要利用多维度的信息进行综合迭代及滤波计算,收敛时间往往比较长,且定位精度受多种因素影响,定位效果不佳。因此亟需研究一种单站无源定位算法,满足定位精度高、收敛速度快、软硬件实现代价低等要求[9]。

针对上述迫切的应用需求,本文提出基于网格搜索的被动单站旋转定位算法。首先推导被动旋转双天线接收信号相位差计算公式,说明相位鉴别模糊产生机理;然后对目标所在水平面进行二维网格划分,利用真实目标方向照射的理论相位差与测量相位差之间存在整数倍相位模糊的特性,建立基于最小化模糊数的定位优化函数;最后采用“粗搜+精搜”的方式对优化函数进行二维峰值搜索,从而获得目标定位结果。

1 旋转天线接收信号相位分析

被动单站旋转定位数学模型如图1所示。假设在空间直角坐标系oxyz下,目标位置点T的坐标为(xT,yT,0);运动平台位置起始点A的坐标为(0,0,H),其中H为平台高度;在初始时刻t0,目标与运动平台之间的方位角和俯仰角分别为α0,β0,平台从点A开始以速度v沿着y轴正向做匀速直线运动;平台上旋转天线基线半径为r,天线基线与x轴的初始夹角为θ0;天线绕着轴线AC逆时针旋转,旋转角速度为ω。

图1 被动单站旋转定位数学模型

α0,β0可表示为

则在初始时刻t0,旋转双天线侦测信号的相位差可以表示为

式中:f为侦测信号频率;c为光速。

同理,在第i(i=1,2,…)次采样时刻ti,目标与被动运动平台之间的方位角αi和俯仰角βi可表示为

其中

式中:Ts为采样周期。在采样时刻ti,被动运动平台旋转天线侦测信号的相位差Δφi可以表示为

在实际工程应用中,鉴相器测量的相位差Δφi的取值范围为[-π,π),测量值与理论值之间存在2π的整数倍相位模糊,即理论相位差

式中:k为相位模糊数。

对相位模糊产生的机理进行仿真。设目标位置坐标为(-71.17 km,30.56 km);平台高度为10 km,平台运动速度为200 m/s;天线基线半径为0.15 m,天线基线的旋转角速度为10 rad/s,天线基线与x轴正半轴之间的初始夹角为随机值;接收信号频率为12 GHz;平台运动过程中,在各采样时刻的两旋转天线接收信号的相位差中加入均方根误差为10°的高斯分布的随机误差,采样时间间隔为10 ms,采样点数为300。被动平台测量相位差与理论相位差的鉴相模糊关系如图2所示。

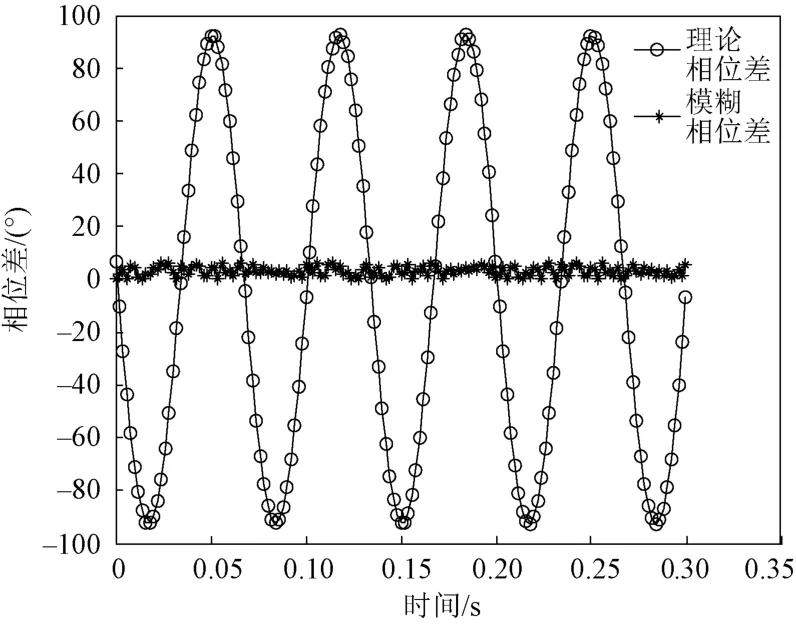
图2 测量相位差与理论相位差鉴相模糊关系

从图2可以看出,只有当旋转天线接收信号的相位差取值范围为[-π,π)时,理论相位差和模糊相位差两条曲线才会重合。由式(6)可知,当4πrf/c＜2π,也就是r＜c/(2f),即天线基线半径小于信号波长的一半时,才不会出现鉴相模糊。本文采用的天线基线半径为0.15 m,所以只有当侦测信号频率低于22.5 MHz时才不会出现鉴相模糊。而常规的雷达信号频率普遍高于400 MHz,因此本定位模型中旋转天线侦测的信号相位一定是存在模糊的。

同时,从式(6)可以看出,侦测信号频率越高,天线基线半径越大,目标与天线旋转平面的夹角越小,越容易出现鉴相模糊。因此必须采用一定的方法消除相位模糊,才能获得准确的目标定位结果。

2 单站旋转定位解模糊算法

由图2可知,在一小段时间内,沿直线运动的旋转天线侦测到的信号相位差是呈正弦规律变化的。如果能够消除鉴相器的相位模糊,目标角度计算将变得比较容易。再利用被动运动平台高度和天线接收信号的相位差求解目标角度,即可获得目标的位置坐标,这就是角度交叉定位算法的原理。但是,假如定位算法需要利用测向结果,目标角度测量误差将是一个难以避免的影响因素。经计算,在目标与平台距离为100 km、平台高度为10 km、测向的角度测量误差为1°时,目标的最大定位误差将达到21 km。显然当目标的距离更远、俯仰角更大时,微小的测向角度误差将造成较大的定位误差,这在实际应用中是不允许的。解决这一问题常见的手段是利用卡尔曼滤波算法平滑误差,但这又会增加定位算法的复杂度,导致定位算法收敛时间变长。因此采用卡尔曼滤波不能从根源上保证定位算法满足快速、准确、稳定的要求。

针对被动单站旋转定位,本文提出直接对目标位置进行二维搜索的定位算法。其基本思想是利用真实目标位置对应的理论相位差与实测相位差之间存在的2π整数倍相位模糊关系建立定位优化函数,并通过对优化函数进行二维峰值搜索获得目标定位结果。下面是该定位算法的具体处理过程。

假设目标位置单次测量所需的时间为T0,则在该时间段内,总共可以获得N条旋转基线。N的计算公式为

对目标搜索区域进行网格划分,利用N条旋转基线对搜索网格(m,n)中的目标建立方程组式中:m,n=1,2,…,N分别表示横向和纵向的网格索引号;kmn为当前遍历网格(m,n)对应的相位模糊数;αm,βn分别为当前遍历网格(m,n)中的目标方位角和俯仰角;xm,yn为当前遍历网格(m,n)中的目标横向和纵向位置坐标。由于相位误差的影响,kmn一般为非整数。

建立二维优化函数

式中:round(·)为四舍五入取整函数。二维优化函数示意图如图3所示。二维优化函数最小值对应的坐标即为目标位置坐标。

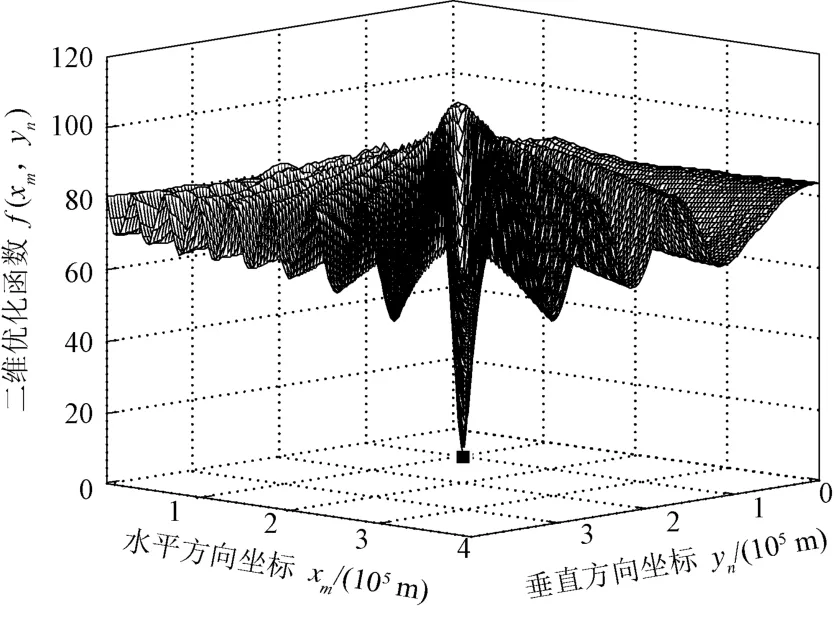
图3 二维优化函数示意图

目标搜索网格划分方法如图4所示。假设目标位于xoy平面内,分别以3 km 为步长建立横向和纵向的目标搜索网格。将网格中心点坐标代入式(8)可求得对应的粗搜索kmn,代入式(9)可求得对应的目标搜索二维优化函数值。f(xm,yn)最小值对应的目标坐标即为粗搜索的目标中心位置(xm0,yn0)。同理,以粗搜索目标位置(xm0,yn0)为中心,上下、左右分别延伸5 km,并以0.2 km 为步长进行精搜索。f(xm,yn)最小值对应的目标位置即为精搜索的目标位置(xce,yce)。

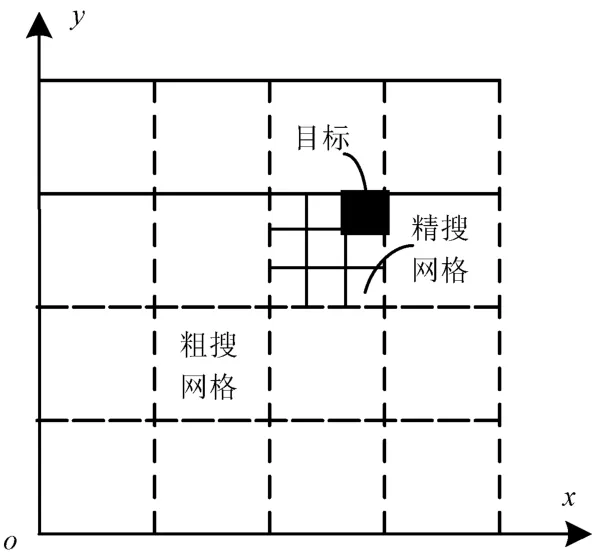
图4 目标位置网格搜索示意图

为了进一步评估定位算法的优劣,采用定位距离误差e作为定位效果的衡量指标。其表达式为

其中

式中:L0,L分别为目标与被动运动平台之间的真实距离和测量距离。

结合式(8)～式(10)可以看出,定位误差的影响因素主要包括信号频率测量误差、目标位置测量误差、相位测量误差等。后续仿真实验将重点考虑以上关键因素对定位算法的影响。

3 仿真实验及结果分析

3.1 频率对定位结果的影响分析

仿真条件:目标坐标为(-259.350 km,347.490 km);被动运动平台高度为18 km,运动速度为200 m/s;天线基线半径为0.15 m,天线旋转角速度为8 rad/s;侦测信号频率为(1～40)GHz;在各采样时刻单次测量的两个旋转天线侦收信号的相位差上加入均方根误差为5°的随机分布噪声,采样间隔为1 ms,总采样时间为200 ms。侦测信号频率对定位结果的影响如图5所示。

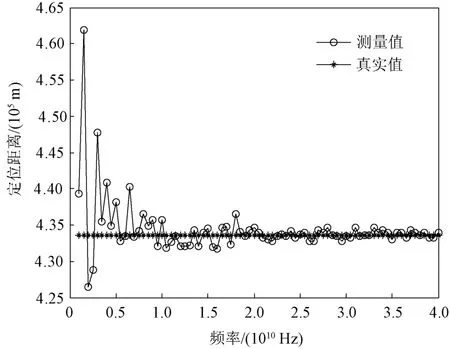
图5 侦测信号频率对定位结果的影响

由图5可以看出,不同侦测信号频率对定位结果的影响不同,大致趋势是频率越高,定位误差越小,频率越低,定位误差越大。经统计,侦测信号频率在(1～40)GHz范围内对应的距离向定位误差均优于5‰。

3.2 目标位置对定位结果的影响分析

仿真条件:目标在水平(-400～400)km、垂直(0～400)km 范围内随机分布,目标总数为80;被动运动平台高度为18 km,运动速度为200 m/s;天线基线半径为0.15 m,天线旋转角速度为10 rad/s;侦测信号频率为12 GHz;在各采样时刻,在单次测量的两个旋转天线侦收信号的相位差上加入均方根误差为10°的随机分布噪声,采样时间间隔为1 ms,总采样时间为300 ms。目标位置对定位结果的影响如图6所示。

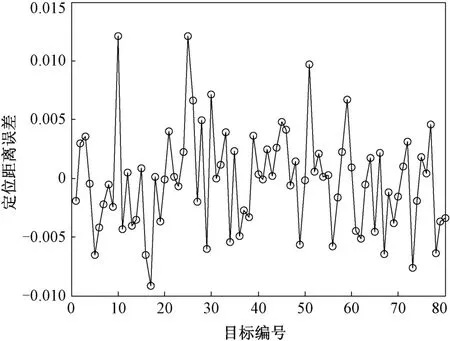
图6 目标位置对定位结果的影响

由图6可以看出,对于不同位置的目标,定位距离误差一致性较好,且均小于2%。可知,本文算法对不同位置的目标的定位性能优良。

3.3 相位噪声对定位结果的影响分析

仿真条件:目标坐标为(-131.160 km,33.756 km);被动运动平台高度为18 km,运动速度为200 m/s;天线基线半径为0.15 m,天线旋转角速度为10 rad/s;侦测信号频率为5.6 GHz;在各采样时刻,在单次测量的两个旋转天线侦收信号的相位差上加入均方根误差为0°～31°的随机分布噪声,采样时间间隔为1 ms,总采样时间为200 ms。相位噪声对定位结果的影响如图7所示。

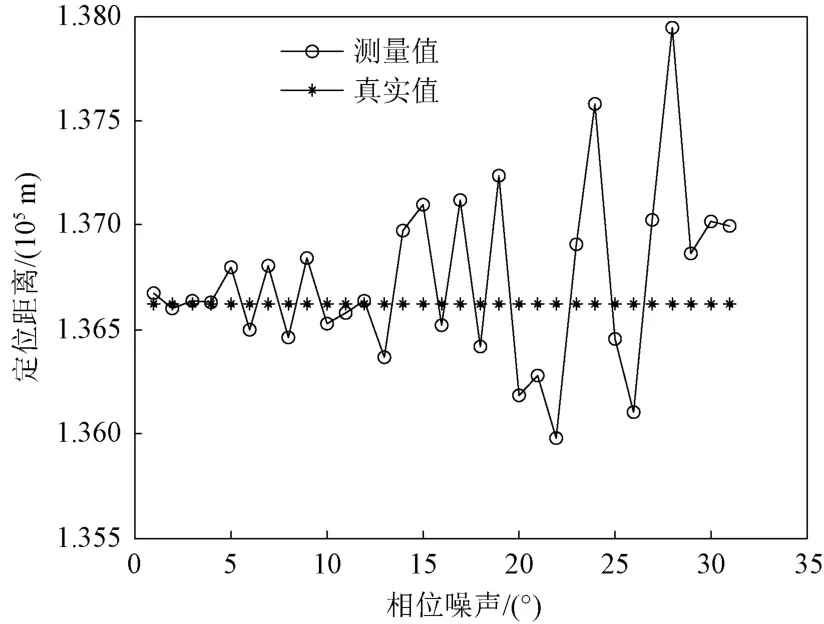
图7 相位噪声对定位结果的影响

由图7可以看出,不同相位噪声对定位结果的影响不同,相位噪声越大,定位距离误差越大。当相位噪声超过17°时,定位距离误差约为4‰。可知,本文算法具有较强的抗相位噪声干扰的能力。

3.4 不同定位算法定位性能分析

仿真条件同3.1节,不同定位算法定位结果如图8所示。可知,本文所提定位算法与传统角度交叉定位算法相比,定位精度提升较为明显。

4 结束语

因传统单站无源定位算法存在定位精度低、收敛时间长、算法复杂度高等不足,针对单站被动运动平台对目标定位的应用需求,本文提出了一

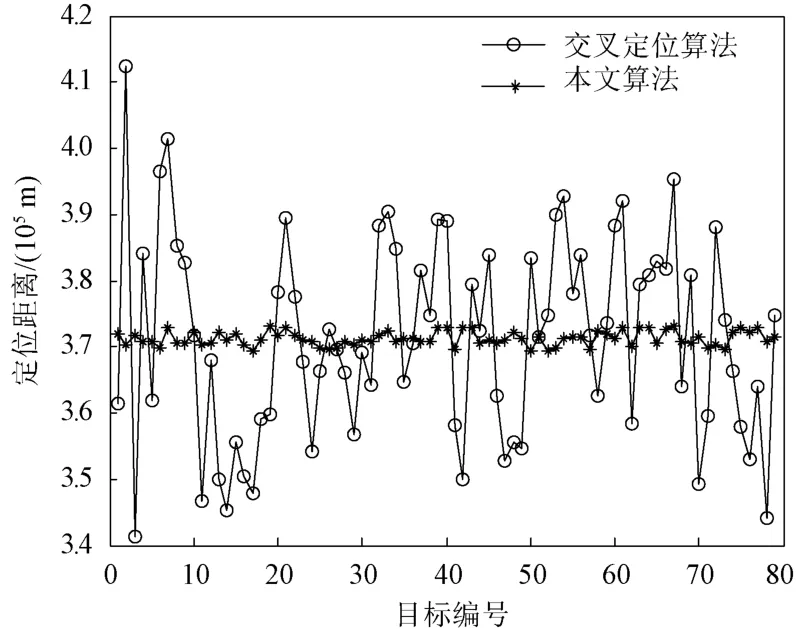
图8 不同定位算法定位结果对比