光电卷积神经网络的光学实时训练算法

顾子煜,张 弦,施君南,高叶盛

(1.上海交通大学电子工程系,上海 200240;2.上海无线电设备研究所,上海 201109)

0 引言

作为合成孔径雷达(SAR)的一个重要研究方向,目标分类识别算法的研究已经开展多年,并且新的算法层出不穷。与传统方法相比,深度学习为SAR 目标分类识别算法的研究提供了一个很有前景的发展方向。通过对SAR 目标特征的学习,神经网络可以以极高的效率与准确率实现目标识别[1-2]。但是,为了解决复杂的SAR 目标识别问题,需要不断更新神经网络的架构,而在数字平台实现深层神经网络则会带来较重的运算负担。并且,由于受到摩尔定律的影响,数字硬件的处理速度面临晶体管尺寸的限制。因此,寻找新运算方式的需求变得愈加迫切和必要。

近年来,通过光学平台实现神经网络的方式逐渐成为研究人员关注的焦点。光学平台凭借其超快的处理速度和并行性的特点,在实现大规模矩阵运算方面具有先天优势。研究人员基于现有的光学神经网络架构,对多种数据集进行了高精度的目标分类,证明了该方法的可行性。

在之前的研究中,研究人员已成功构建了光电卷积神经网络(optronic convolutional neural network,OPCNN),并基于运动与静止目标获取与识别(moving and stationary target acquisition and recognition,MSTAR)数据集完成了目标分类[3-4]。OPCNN 训练阶段依然通过数字方式实现,而验证阶段所有的运算操作均由光学方式实现,从而大大减少了数字平台的运算量。同时,如何减少通过数字方式实现的训练阶段的运算量、加快处理速度依然是一个亟待解决的难题。并且,将在数字平台上训练好的参数加载到光学平台上时,实际光学平台的系统误差会导致参数失配,从而影响实际系统的分类精度,因此平台不一致带来的影响也需要解决。

为了解决上述问题,提升实际应用中基于OPCNN 的SAR 目标分类精度,本文提出一种光学实时训练算法,直接在光学平台上对OPCNN的网络框架进行训练。基于该算法,OPCNN 的正向传播以及反向传播过程均通过同一个光学系统实现,而且在训练阶段占用大量运算资源的梯度求导也通过光学计算实现,以减少数字器件的运算量。为了能够在训练过程中实时更新训练参数,使用可编程的空间光调制器(SLM)进行参数加载。现有研究成果已证明SLM 可以用于SAR目标的高分辨率实时成像[5]。最后在光学平台上使用MSTAR 数据集对OPCNN 进行训练,并采用训练好的网络对目标进行分类,验证所提实时训练算法的可行性。

1 光学反向传播算法

在基于光学平台的实时训练算法中,由于光学计算高速并行的特点,整个网络的处理速度受网络参数规模的影响较小,因此在OPCNN 中无需加入降采样层以减少参数数量。整个网络框架仅包括必须的卷积层、非线性激活层与全局平均池化层。所有卷积层包含相同数量的通道,并且上一层卷积层中各通道的输出将作为下一层卷积层对应通道的输入。卷积层中的通道数量与目标的类别数量相关,二者成整数倍数关系。本文使用的MSTAR 数据集包含10 类目标,因此在OPCNN 的每层卷积层中设置40 个卷积通道。在输出层,所有40 个卷积通道的输出通过sCMOS相机采集,并在后续数字平台中通过叠加操作处理为10类输出,其中每类输出对应于一个目标类别。在经过全局平均池化操作后,这10类输出中的最大值对应的目标类别就是OPCNN 对输入目标的预测类别。这10 类输出与真实值的差值将用于计算损失函数,并用于后续反向传播过程中网络参数的更新。

在之前的研究中,已经推导了OPCNN 正向传播的表达式,为了便于推导反向误差梯度,首先需要将OPCNN 正向传播的表达式改写为矩阵相乘的形式。根据傅里叶光学理论,傅里叶变换可以通过由傅里叶透镜组成的光学2f系统实现,其中f为焦距。在该系统中,输入图像被放置在傅里叶透镜的前焦距面上,那么在透镜的后焦距面上就可以获得输入图像的频谱信息。考虑到时域中的卷积操作可以转换为频域中的点乘操作,首先通过光学2f系统获得输入图像的频谱,然后与卷积核的频谱进行点乘,点乘后的结果再次通过一个光学2f系统进行傅里叶逆变换,变换后的输出即为输入图像与卷积核的卷积结果。将这种由两个光学2f系统组成、可以实现卷积操作的光学结构称为光学4f系统。一幅M×M像素的输入图像经过光学4f系统后的输出可以表示为

式中:Ukn表示第n层卷积层中第k个通道的输出矩阵,其规模为M2×1;P表示傅里叶算子矩阵;Wkn=diag（exp（jΦkn））表示第n层卷积层中第k个通道的卷积核矩阵,其中diag(·)为对角矩阵函数,Φkn表示该通道卷积核频谱的相位矩阵。Φkn是OPCNN中待训练的参数,这里仅选择相位值。

OPCNN 的正向传播和反向传播过程通过同一个光学系统实现,利用sCMOS相机和波前传感器记录输出图像的幅度信息和相位信息。为了方便记录,构造了光学4f系统来延伸输出平面。在反向传播之前,通过复数场生成模块(complex field generation module,CFGM)生成复数误差光场。将双向传播过程中记录的光场输入计算机,通过简单的计算得到梯度结果。更新后的训练参数被重新加载到空间光调制器上,用于下一轮的实时训练。

将相位信息作为待训练参数的原因是其在信号重建、傅里叶变换等操作中起主导作用。第N层(最后一层)卷积层中第k个通道的输出矩阵UkN可以表示为

式中:Uk0表示输入图像矩阵。使用sCMOS相机在输出平面上记录光场的能量谱,并计算出幅度信息。由于取模运算的形式,可以在输出端为网络引入非线性。获得输出光场的幅度信息后,后续在计算机上的操作可以表示为

式中:Ok表示第k个通道的卷积输出;|·|为取模运算符;表示叠加操作输出,用于将多通道的输出转换为与目标类别数量相同的输出;m为卷积通道数与目标类别数的比值;表示通过全局平均池化的输出;avg(·)表示全局平均池化操作;表示softmax归一化操作输出;L表示交叉熵损失函数;Ti表示真实值。

推导得到OPCNN 网络的正向传播表达式后,需要再通过梯度下降算法训练参数,以降低损失函数值。最优的训练参数对应最小的损失函数值。损失函数L对待训练参数Φkn的梯度可以表示为

式中:*为复数共轭运算符;Re(·)为取复数实部函数;tile(·)m表示将矩阵拓展平铺m次,对应式(3)的叠加操作;upsample(Oisoftmax-Ti)M2×1表示升采样过程,对应于式(3)中的全局平均池化操作,Oisoftmax-Ti经升采样后输出矩阵的规模为M2×1,并且矩阵中所有元素的值为(Oisoftmax-Ti)/(M×M);⊙为点乘运算符;T 为矩阵转置运算符。根据式(4),可得到误差光场Ek的表达式

可以发现式(5)可直接求解。接下来需要求出最后一层卷积层的输出UkN对每一层待训练参数Φkn的梯度。通过化简,该梯度可以表示为

则式(4)可以化简为

令

则式(7)可以化简为

式中:Fkn表示在正向传播过程中,衍射光经过第n层卷积层的卷积核Wkn后的光场;Bkn表示在反向传播过程中,衍射光经过第n层卷积层的卷积核Wkn前的光场。无论是正向传播时的光场Fkn,还是反向传播时的光场Bkn,二者均可在同一个光学系统中测得。而根据式(9),损失函数关于训练参数的梯度则可以通过这两个光场的信息直接求解。

在计算出误差梯度后,可得到各卷积层的更新参数

式中:η表示学习率。更新后的参数将加载到光路中继续下一轮的训练,直到损失函数收敛且低于设定阈值。

根据前文提出的光学反向传播算法设计的光学实时训练系统如图1所示。为了测量正向传播时的光场Fkn与反向传播时的光场Bkn,用sCMOS相机记录光场的幅度信息,用波前探测器记录光场的相位信息。由于在光学系统中用于加载信息的空间光调制器无法同时调制幅度与相位信息,因此为了生成反向传播时所需的误差光场Ek,需构建复数场生成模块(CFGM)。CFGM 主要由一个光学4f系统与一个低通滤波器组成。

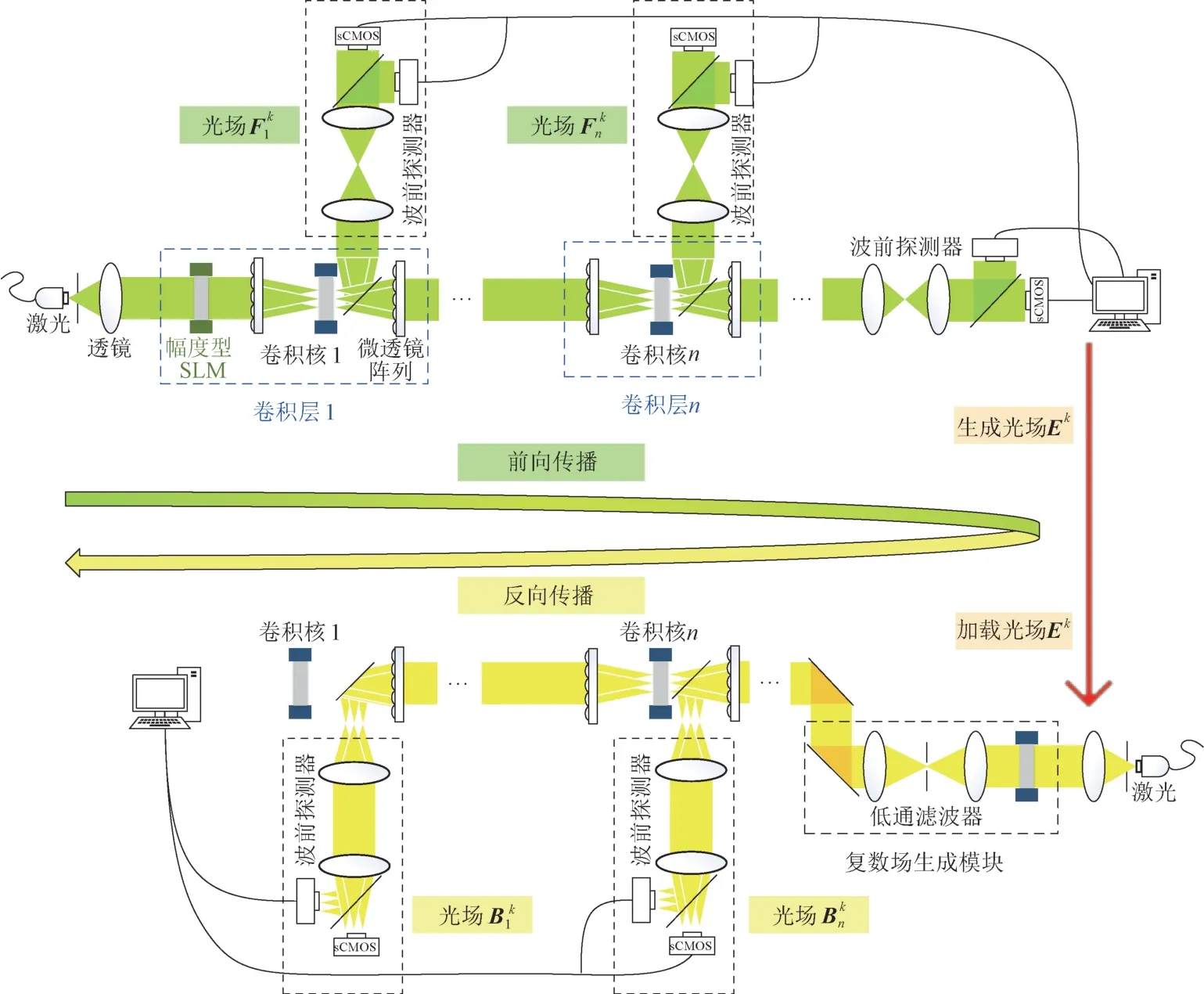
图1 光学实时训练系统示意图

2 实验结果

为了验证所提光学反向传播算法的可行性,首先分别采用通过数字图形处理器(GPU)训练出的OPCNN 与通过光学系统实时训练出的OPCNN,对同一个数据集进行目标分类,并对分类精度进行比较。所提光学系统通过空间光调制器(Pluto-2,Holoeye)加载输入图像及卷积核信息,在空间光调制器间使用微透镜阵列(Edmund optics)组成多通道光学4f系统,用于实现并行的多通道卷积运算,其中微透镜阵列焦距f=30 mm,直径φ=2.0 mm。在输出端,使用ORCA-Flash 4.0 V3 sCMOS 相机(C13440-20CU,Hamamatsu)测量光场的幅度信息,用波前探测器(Phasics SID4)测量光场的相位信息。由于系统中使用的透镜焦距较短,为了便于测量式(8)中透镜前后的光场,通过另一个光学4f系统(f=250 mm,φ=25.4 mm,Thorlabs)将输出光场的位置延伸至探测器处。整个光学系统被波长为532 nm 的激光波束照射,包含1个非线性激活层、1个全局平均池化层和4个卷积层,且每个卷积层中都包含有40个独立的卷积通道。实验中输入图像与卷积核的尺寸均设置为28×28像素。光学实时训练通过上述光学系统实现,而数字训练则通过台式计算机进行(GPU:NVIDIA TITAN RTX),使用版本3.5.0 的Python 与Py Torch 框架。训练与验证时均使用MSTAR数据集中的SAR 目标图像,训练集包含2 747张图片,测试集包含2 425张图片,训练轮数为20,训练时的学习率为0.01。训练OPCNN 的正向传播过程时,所有卷积操作在光学系统上实现,全局平均池化和softmax归一化等计算量少的操作在数字平台上进行。通过不同方式训练的OPCNN 的目标分类性能如图2所示。

图2 通过不同方式训练的OPCNN 的目标分类性能

从图2 可知,通过光学系统实时训练的OPCNN 的分类精度收敛曲线与通过数字平台训练的OPCNN 的分类精度收敛曲线保持一致,且总分类精度分别可以达到93.30%与93.61%,分类精度近似。虽然在光学系统中存在系统误差,但通过光学系统训练出的最优参数是在考虑系统误差的情况下得到的,因此光学系统的实际表现相较于之前的网络有巨大提升,更接近数字训练时得到的仿真结果。通过光学系统实时训练出的OPCNN 在对MSTAR 数据集中SAR 目标进行分类时的混淆矩阵及分类精度如表1所示。

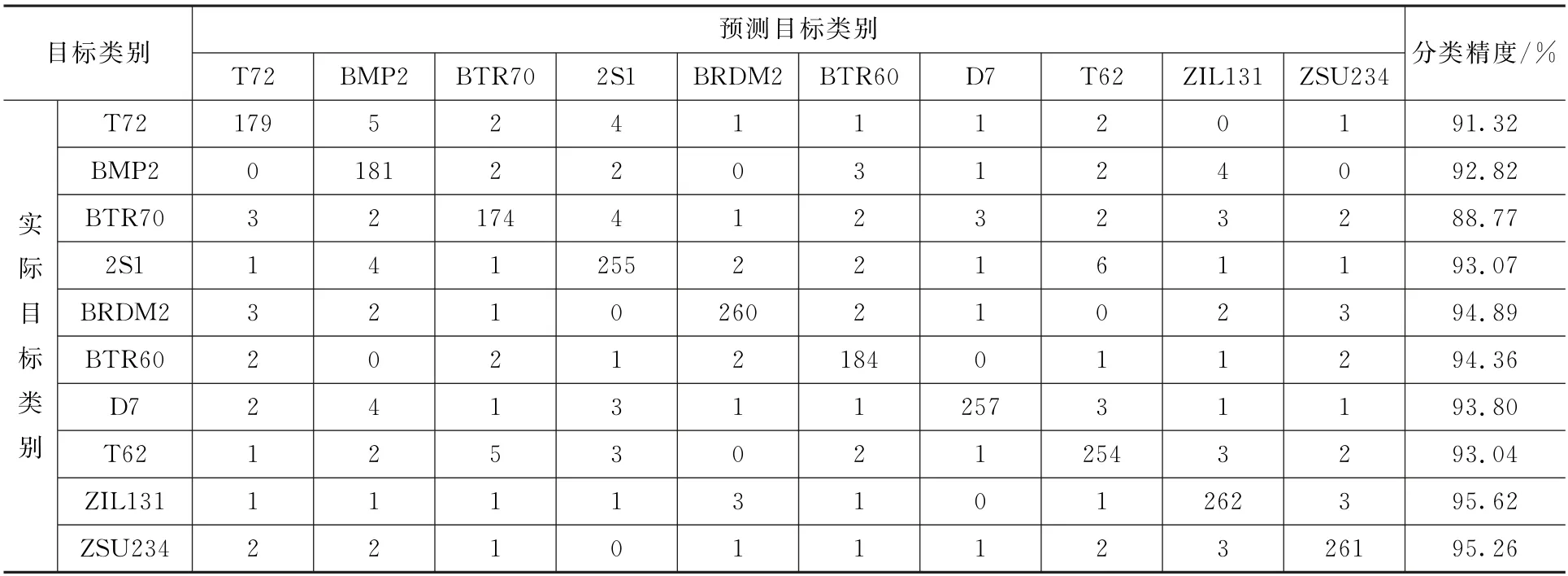
表1 通过光学系统实时训练的OPCNN 对MSTAR 数据集进行目标分类的混淆矩阵及分类精度

接下来讨论卷积层中通道数对网络目标分类精度的影响。因为本文使用了独立的卷积通道对目标进行特征提取,通道与通道之间不会进行特征信息的交互,因此通道数量将决定卷积层对目标特征的提取程度。通过图2(d)可以发现,面对MSTAR 数据集中复杂的目标图像,如果将卷积通道数由每层10个增加到每层40个,对应的网络目标分类精度将由66.07%提升到93.30%。实验结果表明,由独立卷积通道构成的OPCNN可以通过增加通道数,提高对数据集中复杂目标的分类能力。并且由于光学计算的并行特性,通道数的增加不会对整个系统的运算速度产生影响,从而大大弥补了数字计算在该方面的缺陷。

为了定量说明光学计算的优势,比较了同一个OPCNN 分别通过光学训练与数字训练时,单次训练过程所需的时间与运算量。对于光学训练,单次训练所需的总时间Ttot由3部分组成,分别是数据加载到空间光调制器上的时间Tenc、光在光学系统中的传播时间Tprop与测量光场所需的时间Tmeas。对于数据加载所需的时间,空间光调制器的刷新速率为60 Hz,因此每次刷新需要1/60 s。光在光学系统中的传播时间与光路规模和光速的比值有关,由于二者数量级的差距,光的传播时间仅为微秒量级。对于采集数据所需的时间,sCMOS相机的采集速率为80 Hz,波前探测器的采集速率为60 Hz,因此每次采集的时间近似为1/60 s。因为光学训练时需要进行一次正向传播和一次反向传播,因此单次训练所需的总时间可以表示为

则光学训练所需要的总时间约为1/15 s,而在数字训练中,同样的流程则需要0.45 s,远远大于光学训练所需的时间。

由于使用光学训练代替了数字训练,训练过程中大部分的运算操作均通过光学计算的方式实现,因此大大减轻了数字处理器的运算负担。对于一幅M×M像素的待分类输入图像,在数字处理器中进行一次卷积操作需要3M3次复数矩阵乘法与3M2(M-1)次复数矩阵加法,也就是6M2(4M-1)次实数运算。对于一个包含N个卷积层,每个卷积层包含K个卷积通道的OPCNN,通过光学训练减少的实数运算量可以达到12NKM2(4M-1)次。

3 结论

本文提出了一种光学反向传播算法,并在光学系统上实现了神经网络的训练,训练好的网络可以进行复杂的SAR 目标分类。采用光学实时训练系统,神经网络在正向传播与反向传播过程中的大量运算均在光学平台上进行,从而大大减少了数字处理器的运算量。基于MSTAR 数据集对OPCNN进行训练与测试,结果验证了所提算法的可行性。对OPCNN进行光学实时训练,得到的网络能够克服光学系统中的系统误差影响,获得最优的训练参数,保持与仿真结果近似的分类性能。这种较强的鲁棒性有助于OPCNN 在实际应用中实现稳定高效的SAR目标分类识别。