数据链航迹延迟与ESM点迹间断融合跟踪

傅 伟，余 远，谭顺成，3

（1.海军航空大学，山东 烟台 264001；2.山东工商学院计算机科学与技术学院，山东 烟台 264003；3.南京电子技术研究所，江苏 南京 210039）

0 引言

在现代作战系统中，仅依靠单传感器提供的信息对目标进行跟踪效果非常有限，且一旦被敌方电子侦察系统截获并实施干扰或打击，传感器的跟踪性能会急剧下降甚至失效[1]。未来的陆海空天战争中，复杂的电磁环境[2-3]、日益完善的目标隐身技术[4]以及不断提升的装备智能水平[5-6]，给传统的目标探测跟踪带来了极大的挑战[7]；同时，现有传感器中并没有各项性能指标均独占鳌头的传感器，单个传感器跟踪系统已经很难适应多元化的战场环境。

为了更加有效地提高机载多平台多传感器系统的性能，综合利用这些传感器在功能与性能上的优势，达到单个传感器无法实现的作战效果，就须要在平台间对这些传感器的数据进行传输、融合，从而将其构成1 个完整有效的互补体系[8]。数据链和电子支援系统（Electronic Supporting Measures，ESM）作为机载传感器系统中的重要组成部分[9]，对如何将信息和数据进行综合分析和处理，实现功能与性能互补，进而获取更加精确的目标状态和属性，分析敌方行为意图[10]、态势评估以及威胁分析等发挥着重要作用，在机载预警信息综合处理与现代综合电子战中占有重要位置[11]。

然而，在融合跟踪过程中：一方面由于量测数据预处理以及通信延迟等因素的影响，数据链航迹会存在一定的延迟，且延迟时间是未知的；另一方面，在现代战场环境下，传感器通常会采取间歇工作模式，尽可能减少工作时间，以降低其被侦察和干扰的概率[12-13]。因此，如何实现数据链航迹存在延迟和ESM点迹间断情况下的数据链航迹与ESM点迹融合跟踪，并提升融合跟踪的精度，是1个须要解决的现实问题。

本文针对数据链航迹存在延迟和ESM 点迹间断情况下的数据链航迹与ESM点迹融合跟踪，提出了复杂情况下的数据链与ESM融合跟踪方法，并对其融合跟踪的精度进行分析研究，为信息综合处理装备的发展提供借鉴。

1 总体方案

本文的基本思路是：首先，对数据进行时间对准，保证数据链和ESM 的数据率和时间节点的一致；然后，通过构造基于不敏变换（Unscented Transformation，UT）的非线性量测转换和误差估计方法，将数据链数据从载机北东下（North East Down，NED）坐标系配准到ESM 数据的极坐标系；最后，通过引入随机补偿机制对数据链延迟进行补偿，并与ESM数据进行关联融合，总体方案如图1所示。

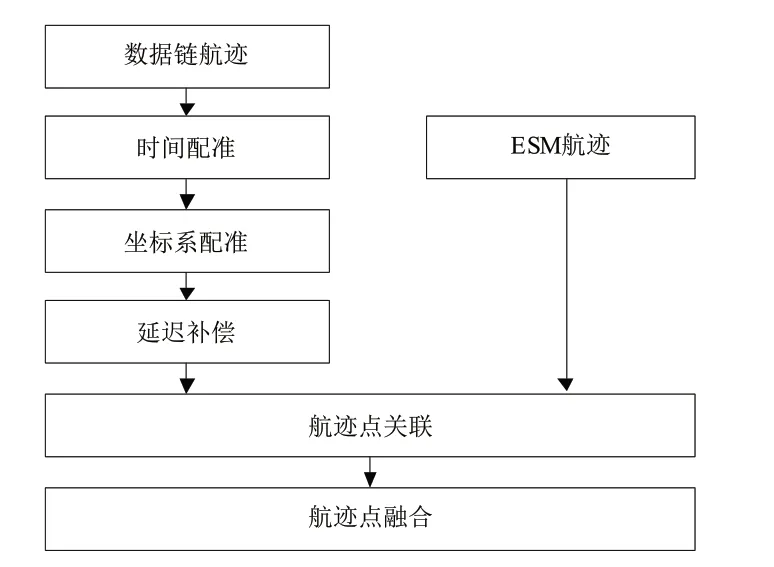
图1 总体方案Fig.1 Overall plan

2 算法实现

2.1 时间配准

使用拉格朗日三点插值法把数据链的数据配准到ESM的时间点上，即将高精度的观测数据推算到低精度的时间点上，具体为：在同一时间段内将各传感器提供的航迹点按测量精度进行增量排序；然后，将高精度观测数据分别向最低精度时间点内插、外推，以形成一系列等间隔的目标航迹点。

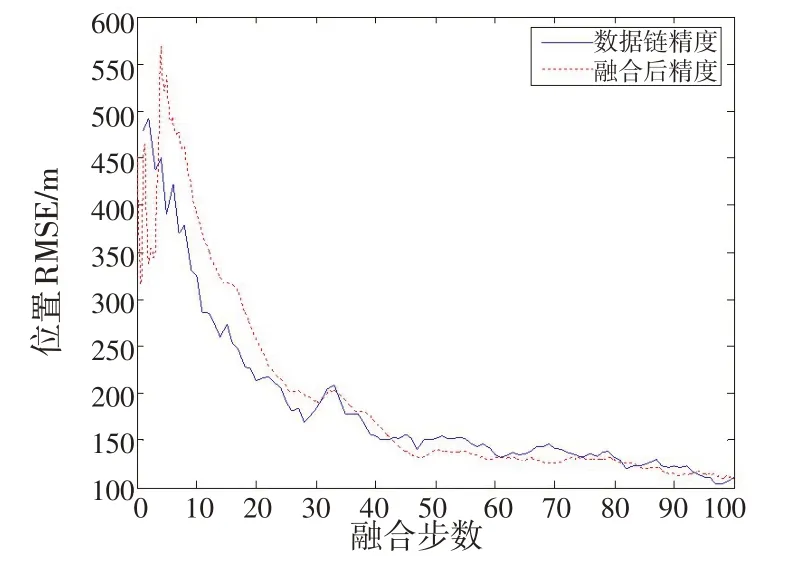
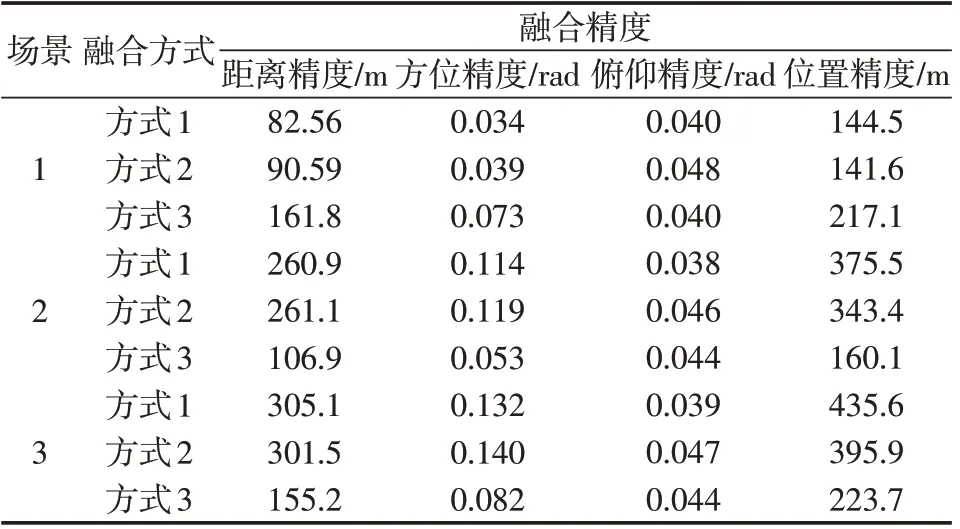
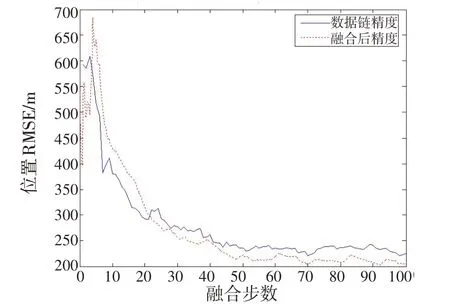
假设tk-1、tk、tk+1时刻有数据链航迹点Xdata,k-1、Xdata,k、Xdata,k+1，则计算ti时刻（tk-1

若（tk-1，Xdata,k-1）、（tk，Xdata,k）、（tk+1，Xdata,k+1）这3点不在1条直线上，则上述插值公式得到的是1个二次函数，通过这3点的曲线是抛物线。

2.2 空间对准

因为数据链提供的航迹点为NED 坐标系下的直角坐标形式，而ESM 提供的航迹点为极坐标形式，因此，需将NED直角坐标形式的数据链数据转换成极坐标形式，同时，将NED 直角坐标系下的量测误差转换成极坐标系下的量测误差（即空间对准），才能进行航迹的关联与融合。假设k时刻数据链的航迹点表示为Xdata,k=(xdata,k,ydata,k,zdata,k)，其中，xdata,k、ydata,k、zdata,k分别表示目标的NED 坐标系下各方向的坐标。量测误差分别为σdata,x、σdata,y、σdata,z，统一到ESM 数据坐标系后表示为Yk=(αdata,k,βdata,k)，其中，αdata,k、βdata,k分别表示目标的方位角和俯仰角，量测误差分别为σdata,α、σdata,β。

鉴于UT 在处理非线性偏差估计[14]、非线性滤波[15]、非线性误差传递[16-17]以及非线性量测转化[18]等方面表现出的突出优势，本文采用UT 对数据链航迹点进行NED直角坐标到极坐标的转换，并得到转换后的量测误差估计。其基本思想为如下。

以NX表示向量Xdata,k的位数，精确选择1 组确定的σ点集，其点集表达式为：

得到相应新的σ点集，变换过程中权值wi不变，则转换的航迹点和量测误差可分别表示为：

式（6）中：

2.3 数据链延迟补偿

数据链随机延迟的存在势必影响融合的精度，因此，考虑对数据链延迟进行补偿。不失一般性，假定数据链延迟Tdelay在区间[Tmin,Tmax]上呈均匀分布，其中Tmin和Tmax表示数据链可能的最小和最大延迟时间，根据数据链延迟分布特性，相应的取随机数：

对数据链随机延迟的数据进行延迟补偿，其中rand( )1 表示在区间[0,1]上按照均匀分布产生1 个随机数。由于

因此，Tmod是Tdelay的无偏估计。值得注意的是，实际采取的延迟补偿策略应根据数据链的实际延迟分布特性进行相应的调整。

2.4 航迹点关联

假设ESM 在k时刻点迹为，i=1,2,…,n，n为点迹数，数据链航迹点转换后的量测(αdata,k,βdata,k)，第i个量测的归一化误差平方为：

则式（10）服从自由度为2的卡方分布。设置显著性水平α，查表可得自由度为2的门限值，若

2.5 航迹点融合

再利用数据链获得的目标距离量测rdata,k对(αfusion,k,βfusion,k) 进行扩维，即获得融合后的航迹点(rdata,k,αfusion,k,βfusion,k)。

3 仿真分析

为验证本文方法的有效性，不失一般性，假设1个2架飞机编队飞行对目标进行融合探测跟踪的场景进行仿真分析。其中，飞机1搭载ESM传感器，飞机2可给飞机1传来数据链航迹，飞机1为机载融合中心，在NED坐标系下处理数据，融合后输出结果。

假设目标相对飞机均做匀加速直线运动，总仿真时间为T=10 s，ESM 的方位角和俯仰角测量均方根误差σESM,α=σESM,β=0.3，测量周期TE=0.1 s，等间隔间断8次，ESM关机时间占总工作时间的20%；数据链在X、Y和Z方向上测量均方根误差σdata,x=σdata,y=σdata,z=300 m，测量周期TR=1 s，数据链最小和最大可能延迟时间分别为Tmin=50 ms 和Tmax=1 000 ms，以场景1、2 和3 分别表示数据链实际延迟时间的100 ms、700 ms和1 000 ms这3种场景，而方式1、2 和3 分别表示仅采用数据链数据、无延迟补偿数据链和ESM融合以及有延迟补偿数据链和ESM融合这3 种融合方式，对不同数据链延迟场景下采取不同融合方式的融合精度进行仿真分析和对比，由T=10 s 和TE=0.1 s 可知总融合步数为N=100 。图2～7给出了不同场景下无延迟补偿和有延迟补偿融合方式的融合精度对比。

图2 场景1下无延迟补偿的融合精度Fig.2 Fusion precision without delay compensation under scene 1

图3 场景1下有延迟补偿的融合精度Fig.3 Fusion precision with delay compensation under scene 1

表1给出了滤波平稳后3种不同融合方式的融合精度比较，融合精度通过位置均方根误差（Root Mean Square Error，RMSE）的大小表示。

表1 不同场景下不同融合方式的融合精度比较Tab.1 Comparison of fusion precision with different scenesand different fusion methods

由仿真结果可得如下结论。

当数据链延迟较小时（如场景1 所示），由图2、3和表1 中场景1 的延迟补偿前后的精度可以看出，数据链与ESM 数据融合后，数据链、无延迟补偿融合和有延迟补偿融合的位置跟踪精度均值分别为144.5 m、141.6 m 和217.1 m，有延时补偿融合的位置跟踪精度反而比数据链和无补偿融合的位置跟踪精度要差。这是因为数据链实际延迟为100 ms，而本文延迟补偿的均值为525 ms，延迟补偿过度造成位置精度的下降。

当数据链延迟较大时（如场景2、3所示），由图4～7，以及表1中场景2、3的有无延迟补偿融合的位置跟踪精度可以看出：场景2数据链、无延迟补偿融合和有延迟补偿融合的位置跟踪精度均值分别为375.5 m、343.4 m和106.1 m；场景3数据链、无延迟补偿融合和有延迟补偿融合的位置跟踪精度均值分别为435.6 m、395.9 m和223.7 m。有延时补偿融合的位置跟踪精度明显好于数据链和无延迟补偿融合的位置跟踪精度，且延迟补偿值越接近真实的延迟值时，有延迟补偿融合的位置跟踪精度越高（如场景2的仿真结果所示）。

图4 场景2下无延迟补偿的融合精度Fig.4 Fusion precision without delay compensation under scene 2

图5 场景2下有延迟补偿的融合精度Fig.5 Fusion precision with delay compensation under scene 2

图6 场景3下无延迟补偿的融合精度Fig.6 Fusion precision without delay compensation under scene 3

图7 场景3下有延迟补偿的融合精度Fig.7 Fusion precision with delay compensation under scene 3

4 结论

本文提出了1 种复杂情况下的数据链与ESM 融合跟踪方法，有效解决了数据链航迹存在延迟和ESM点迹间断情况下的数据链航迹与ESM 点迹融合跟踪难题，并对融合跟踪的精度进行分析研究。仿真结果证明了该方法的有效性，同时也表明，有延迟补偿时的融合跟踪精度取决于延迟补偿均值与实际延迟的贴近程度，为信息综合处理装备的发展和设计提供借鉴支持。