汽车外后视镜造型对气动和噪声影响的风洞实验研究

付威，王勋年，李勇,3,*

1.温州大学 机电工程学院，温州 325035

2.中国空气动力研究与发展中心 气动噪声控制重点实验室，绵阳 621000

3.温州大学 平阳智能制造研究院，温州 325400

0 引 言

汽车噪声主要包括发动机噪声、轮胎噪声和气动噪声[1]。气动噪声是汽车高速行驶时的主要噪声源[2]。其中，由高速气流在汽车A 柱和外后视镜附近引起的旋涡流动而造成的车窗表面脉动压力是产生气动噪声的主要原因之一[3-4]。改善汽车外后视镜尾流区域涡流运动能够有效降低车窗表面的脉动压力：一方面，可降低外后视镜本身产生的气动噪声；另一方面，可降低壁面脉动压力经车窗传至车内的噪声，提高车内乘客的舒适性。

国外对外后视镜气动噪声的研究早于国内，一般通过计算与实验开展研究。Grahs 等[5]采用不同网格划分策略研究某外后视镜简化模型所产生的气动噪声，发现合理改变外后视镜自身形状参数能有效降低气动噪声。Kim 等[6]采用粒子图像测速技术（PTV）分析了不同外后视镜形状对噪声的影响。Kato[7]提出了一种可以直接计算远场和近场噪声的方法，并阐述了3 种不同形状外后视镜对声场反射的差异。Li 等[8]对某型汽车外后视镜产生的气动噪声进行了风洞实验和数值仿真，结果表明外后视镜产生的气动噪声主要为宽频噪声，且能量主要集中在中低频区域。Mohamud 等[9]的研究结果表明，在CFD 计算中，可以使用宽频噪声Curle 模型分析外后视镜表面噪声源分布情况。Chen 等[10]在商用软件Fluent 中采用大涡模拟（LES）方法分析了不同风速下外后视镜产生的风噪大小，研究结果表明使用DSLM （Dynamic Smagorinsky-Lilly Model）模型比单独使用SLM 模型的计算结果更接近实验结果。Walker 等[11]分析了不同偏航角下汽车外后视镜的振动强度和噪声大小，结果表明：汽车外后视镜在30°偏航角下，抖振和风噪综合最小。Yao 等[12]使用不同计算方法分析了外后视镜产生的内部噪声大小，结果表明：可压缩大涡比分离涡模拟效果好，能更好地解决边界层内的压力波动问题。

国内对汽车气动噪声的研究较晚，最早始于江苏大学对车身外流场的探索[13]。刘红光和陆森林[14]的研究指出偶极子声源在车辆气动噪声中占主导地位。谢超等[15]在商用软件Fluent 中采用不同计算模型对汽车的气动噪声进行仿真计算，结果表明基于Realizable k-ε/LES 混合模型的仿真计算更为准确和高效，且消耗的计算资源更少。陈鑫等[16-17]对比分析了5 款外后视镜的造型特点，发现外后视镜镜罩、基座造型、安装角度等因素对前侧窗区域气动噪声影响较大，对这些因素进行适当调整组合，可有效降低气动噪声。李启良等[18]通过建立主动射流模型来增大外后视镜尾部的时均压力，降低压力梯度，使得整车气动阻力系数降低了0.002，前侧窗表面总声功率级降低了1.8 dB，湍流脉动总声功率级降低了0.3 dB。姜豪等[19]采用分离涡模拟与计算气动声学相结合的方法，对前侧窗表面气动噪声进行了分析，并提出了2 种优化方案。

基于上述研究，本文以一简化的外后视镜模型为基础模型，提出3 种基于外形改变的降噪措施，即外后视镜镜身分别倾斜15°、30°，以及采用椭柱形底座，结合PIV 测试技术、六分量动态天平测力技术和壁面麦克风脉动压力实验，分析外后视镜尾迹区域流场及阻力变化规律，揭示其降噪机理，为低阻力和低噪声外后视镜的结构设计提供可行性方案。

1 模型及实验布置

1.1 风洞与实验模型

实验在温州大学0.5 m×0.4 m 开口射流声学风洞中进行，实验风速为120 km/h。该风洞为开环吸气风洞，最大风速可达60 m/s，湍流度低于0.2%。实验段所处的消声室净空间为3.8 m×3.3 m×2.5 m，截止频率为140 Hz。最大风速60 m/s 下，声学风洞中心轴1.7 m 处的流场背景噪声为70 dB。

基准模型由上、中、下三部分组成，其三维图及工程图如图1 所示。模型上部为半径45 mm 的1/4 球，中部为半径45 mm、高60 mm 的半圆柱，底部为直径25 mm、高30 mm 的圆柱。模型总高H=135 mm，迎风面总宽W=90 mm，高/宽比为1.5。Oxyz 坐标系的原点设置在底部圆柱中心。

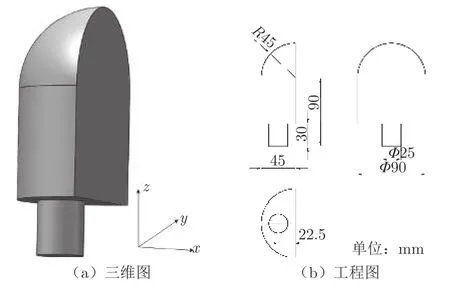
图1 基准模型Fig.1 Baseline model

图2 为3 款造型改进后的模型，其中模型A 为镜身倾斜15°，模型B 为镜身倾斜30°，模型C 的底部为椭圆支撑柱。基础模型与模型C 底部支撑柱横截面上的差异及尺寸如图3 所示。所有实验模型均采用树脂材料以3D 打印技术制作而成。为减小反光对PIV 实验结果的影响，模型采用哑光漆喷涂成黑色，如图4 所示。

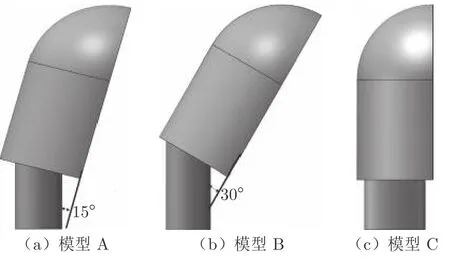
图2 改进模型Fig.2 Improved model

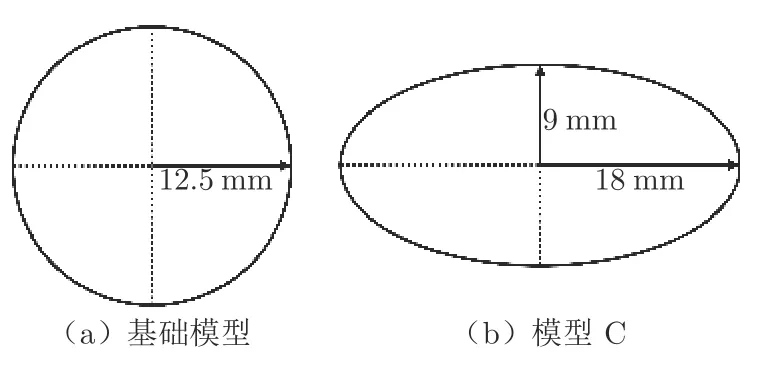
图3 基础模型与模型C 底部支撑柱横截面的差异Fig.3 Diagram of difference between baseline model and model C on a cross-section of the support column

图4 模型实物图Fig.4 Real models

1.2 PIV 测试布置

为分析外后视镜尾迹区域流场变化，对外后视镜进行PIV 实验，图5 为实验模型安装示意图。外后视镜模型安装在一块与风洞出口底面相连的平板上（平板相当于汽车侧窗表面），距离风洞出口160 mm。实验模型横截面堵塞率为4.67%，满足堵塞率小于5%的实验流场要求[20]。实验时主要对3 个截面进行分析：纵截面位于模型正中间y=0 处，横截面1 位于模型中部正中间、距平板壁面60 mm 处，横截面2 位于模型下部正中间、距平板壁面15 mm 处，如图6所示。

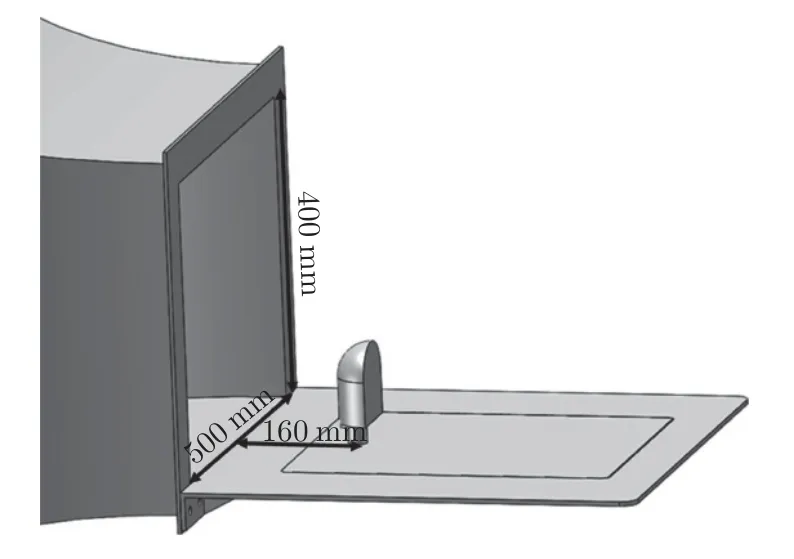
图5 模型安装示意图Fig.5 Model installation diagram

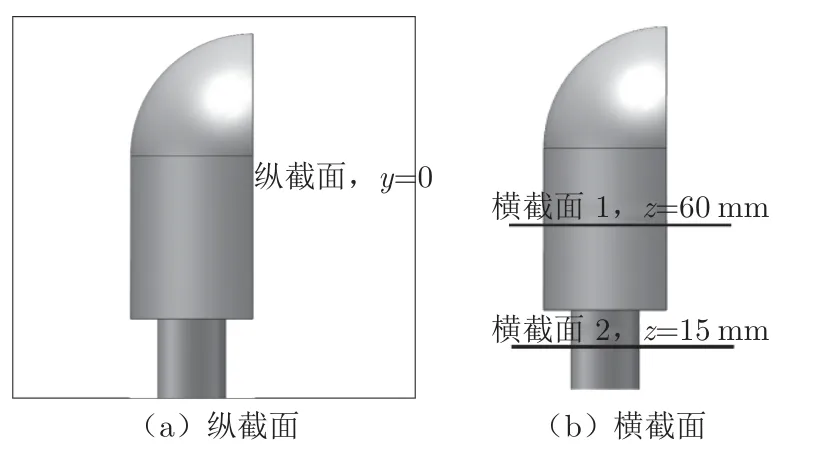
图6 截面分析示意图Fig.6 Diagram of section analysis

流场显示实验采用北京立方天地科技有限公司的PIV 设备，激光测试频率为5 Hz，其安装示意及实物如图7 所示。拍摄纵截面时，激光器位于模型正上方，5M 分辨率的尼康CCD 相机位于激光器垂直位置；拍摄2 个横截面时，激光器与CCD 相机位置互换。

图7 PIV 实验布置图Fig.7 PIV experiment layout

1.3 壁面麦克风测试布置

外后视镜尾迹区域存在的湍流结构不仅会与侧窗玻璃表面作用产生噪声，还会在侧窗上产生脉动压力引起车窗振动，两者组成的混合噪声会通过侧窗传至人耳。与外后视镜尾流旋涡本身产生的湍流噪声相比，旋涡与侧窗表面相互作用产生的脉动压力所引起的气动噪声更加强烈。在该实验中无法直接测量传入内部的气动噪声，因此通过测量外后视镜流场后的壁面脉动压力来定性描述。为对外后视镜作用于壁面的脉动压力进行直观描述，如图8所示，在平板壁面±30°位置由近及远设置3 排共21 个脉动压力监测点，每排相邻监测点间隔10°。第一排与模型底部中心位置距离为135 mm （即3 倍球半径，3R）；第二排为180 mm （4R）；第三排为225 mm （5R）。脉动压力采用型号为BSWA MPA416的麦克风测量，麦克风表面与壁面齐平布置。采样频率为51.2 kHz，采样时间为8 s。总采样数据为100块，每个块的大小为4 096，频率分辨率为12.5 Hz。已有研究表明，尾迹核心区的脉动压力对外后视镜气动噪声的贡献最大[16]，因此本文主要对第一排3、4、5，第二排10、11、12 和第三排17、18、19 这9 个处于外后视镜尾迹核心区的监测点进行频谱和总声压级分析。

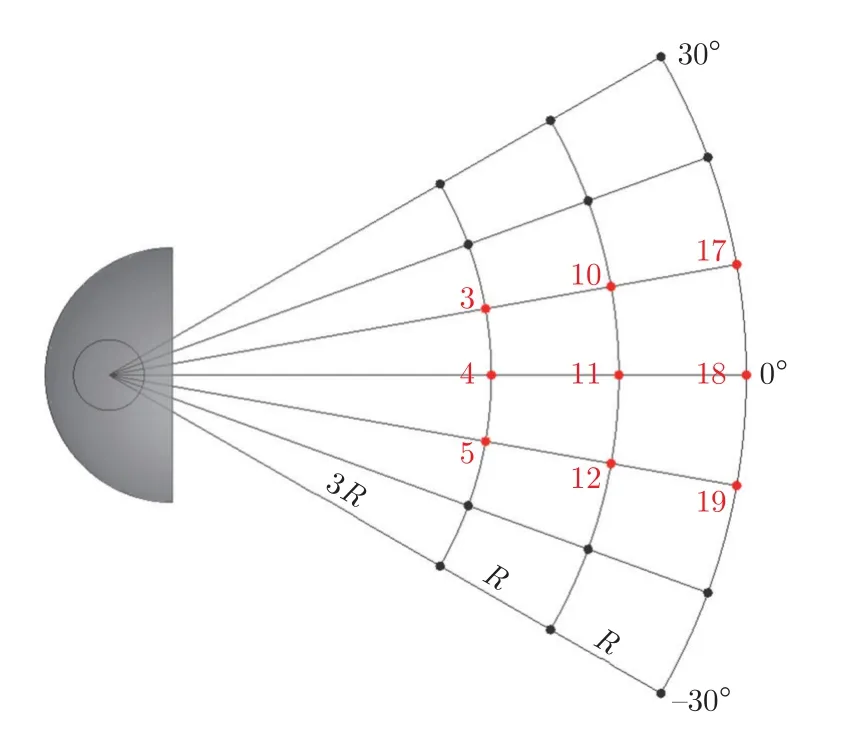
图8 壁面压力监测点布置示意图Fig.8 Schematic layout of wall pressure monitoring points

1.4 六分量天平测力布置

图9 为六分量天平安装示意图，外后视镜模型固定在天平顶端，天平左右与平板之间各空出2 mm间隙，以便检测气流对后视镜的作用力。天平型号为ATI 工业自动化有限公司生产的Mini-45，实验时采样频率设置为7 000 Hz。为减小实验误差，每个模型采样5 次，每次采样30 s，取中间20 s 数据进行均方根分析，得到每次采样的结果，再以其平均值作为最终模型阻力值。

图9 六分量天平安装示意图Fig.9 Schematic installation of six-component balance

2 结果和分析

2.1 声学特性

2.1.1 频谱分析

侧窗壁面脉动压力是产生噪声的重要来源之一，其变化能够反映声源的一定特征。为了更加直观地对比4 款外后视镜在120 km/h 的风速下对侧窗壁面的影响，将麦克风测量的壁面脉动压力的时域信号采用快速傅里叶变换（FFT）转化为频域信号，并与参考声压值pref=2×10-5Pa 对比，得到其声压级（Lsp）频谱图，单位为dB。图10 为基础模型第一、二、三排中间3 个监测点的壁面脉动压力频谱对比图。从图中可以看出，侧边2 个监测点的脉动压力频谱曲线在全频率段较为接近。因此，下文主要对位于正中间位置的4、11、18 和位于一侧的3、10、17 等6 个监测点进行频谱对比分析。

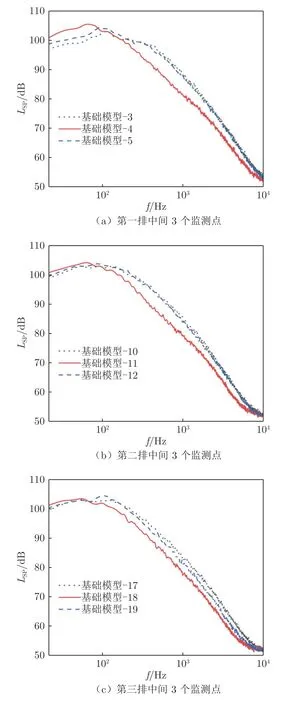
图10 基础模型监测点频谱分析Fig.10 Spectrum analysis of monitoring points of baseline

图11 为所有模型位于第一排的3 和4 两个监测点的频谱对比图，图12 为位于第二排的10 和11 两个监测点的频谱对比图，图13 为第三排的17 和18 两个监测点的频谱对比图。图11～13 还展示了各个监测点的背景脉动压力频谱。从图11～13 中可以很明显地看出，外后视镜所引起的壁面脉动压力具有宽频特性，且能量主要集中在500 Hz 以下的中低频段。在此频段内，麦克风测得的各模型的脉动压力值相差也较大。背景压力是在仅安装平板而未安装外后视镜情况下的测量值，从图中可以看出，在500 Hz 以下频段，背景压力远小于实验模型的脉动压力，差值达10 dB 以上，说明本文的实验数据是可靠有效的。在500 Hz 以上频率范围，各模型的壁面脉动压力相差不大；在1 kHz 以上频段，部分模型的壁面脉动压力甚至低于背景压力。由于2 kHz 以上高频段的壁面脉动压力远小于中低频段，其对总声压的贡献量几乎可以忽略，所以本文主要对中低频段特别是20～500 Hz 范围内的壁面脉动压力进行分析。在500 Hz 以下的中低频段范围，所有造型改进模型对壁面脉动压力的抑制效果都很明显，但在不同监测点，抑制效果存在一定差异。下文将对每个监测点进行具体分析。

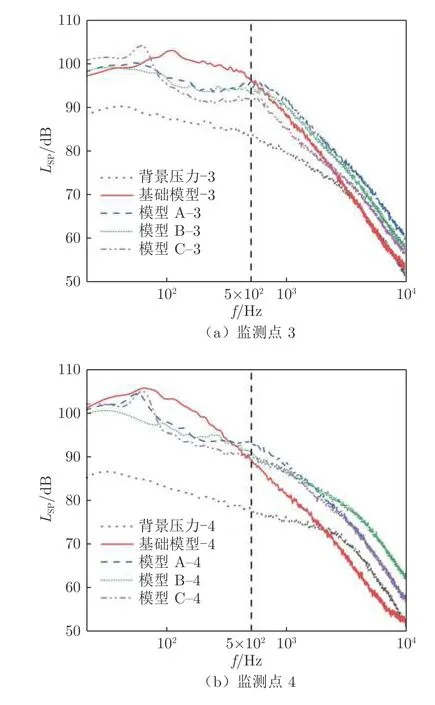
图11 不同模型在监测点3、4 的频谱对比图Fig.11 Spectrum comparison map of monitoring points 3 and 4 in different models

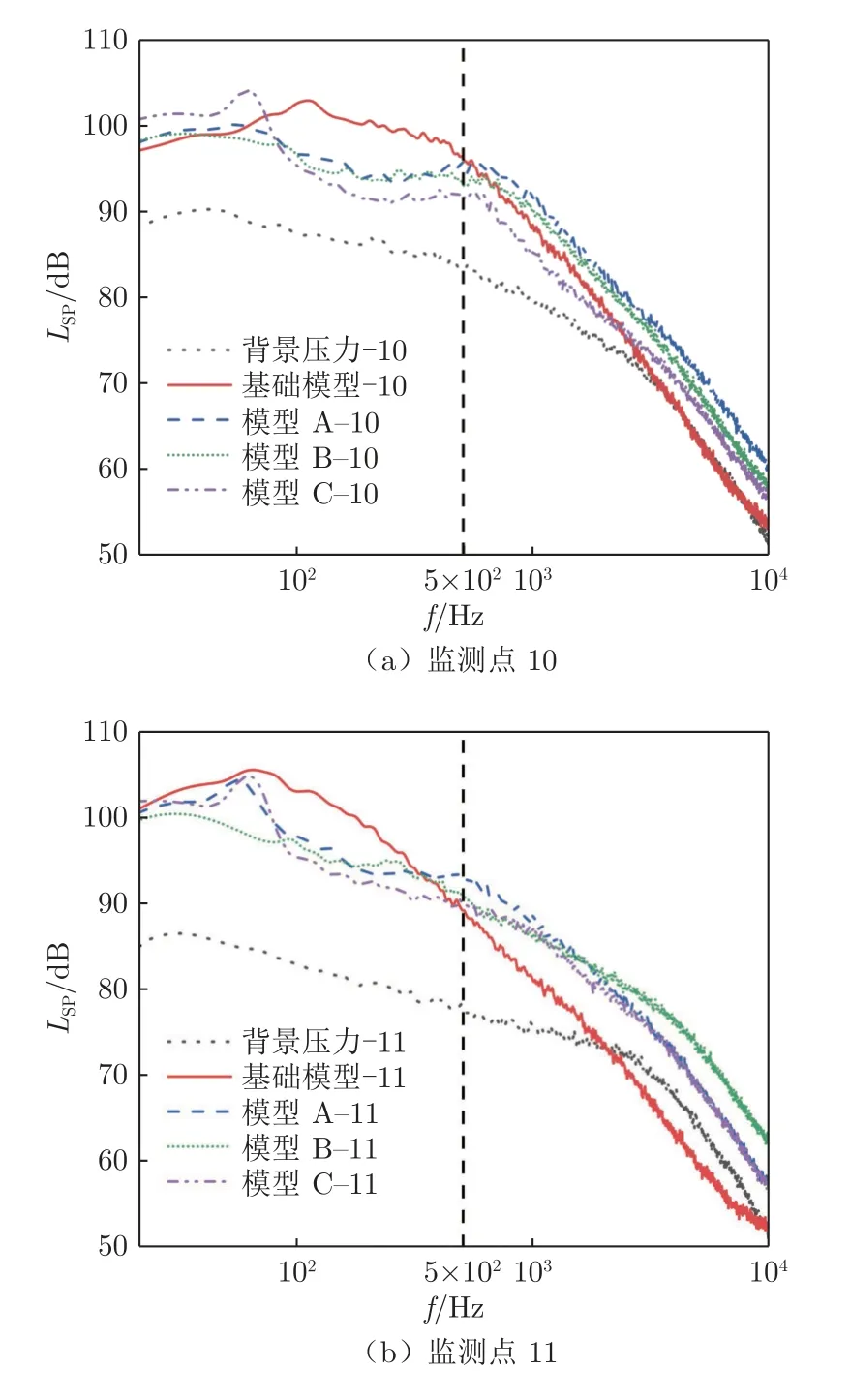
图12 不同模型在监测点10、11 的频谱对比图Fig.12 Spectrum comparison map of monitoring points 10 and 11 in different models

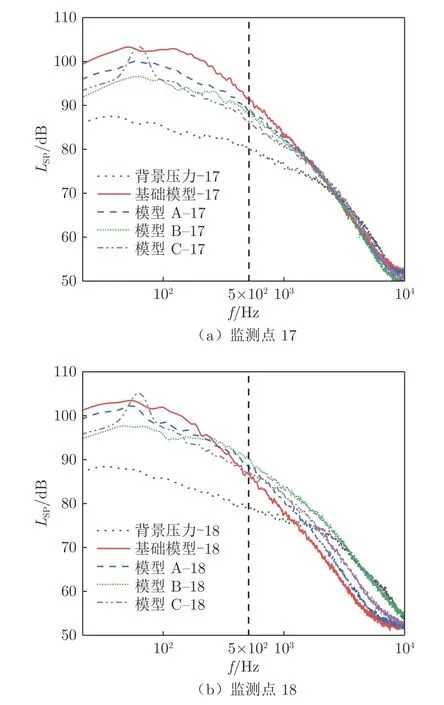
图13 不同模型在监测点17、18 的频谱对比图Fig.13 Spectrum comparison map of monitoring points 17 and 18 in different models

在图11 所示的监测点3、4 中，监测点3 主要降压频段集中在70～500 Hz，监测点4 主要降压频段为70～400 Hz。在此范围，所有改进模型壁面脉动压力始终低于基础模型，模型C 壁面脉动压力最低，模型B 次之，模型A 略高于模型B，但也远小于基础模型。模型C 的监测点3、4 在此范围内最大降压幅度均接近10 dB，模型A 和模型B 在3、4 监测点的最大降压幅度也均超过5 dB。

在图12 所示的监测点10、11 的频谱图中，降压频率向低频范围移动。监测点10 的降压频段分布在20～400 Hz，监测点11 的主要降压频段为20～200 Hz。模型B 和C 在监测点10 的最大降压幅度均接近10 dB，在监测点11 的最大降压幅度超过5 dB，模型A 在这两个位置的最大降压幅度均超过5 dB。

在图13 所示的监测点17、18 中，3 个改进模型在监测点17 的降压频段最广，分布在20～1 000 Hz范围内，但监测点18 的降压频段主要集中在200 Hz以内。在监测点17，模型B 和C 的降压幅度近10 dB，模型A 的最大降压幅度近5 dB；在监测点18，模型B 的最大降压幅度超过5 dB，模型A 和C 的最大降压幅度也超过3 dB。

从图11～13 还可以看出：椭圆柱底座的模型C 在50～70 Hz 之间有一个明显的频率波峰，而其他3 个模型基本没有，说明模型C 流场中可能存在一定的周期脉动。

2.1.2 总声压级分析

表1～3 为9 个监测点的总声压级对比（频率计算范围为20～1 000 Hz）。从表中可以看出，背景总声压级远低于实验模型，证明了本文实验数据的可靠性。改进模型A、B、C 在每个监测点上的总声压级都小于基础模型，最大降压点均在监测点17，分别降低了3.8，6.0 和5.3 dB。由于外后视镜尾部湍流在侧窗上产生的气动噪声是其作用在侧窗面积上的综合效应，因此，不同模型的综合降噪效果分析须集合所有监测点的数据。表4 是在不同频率范围内3 个改进模型声压级相对于基础模型的降压效果，表中ΔLsp为改进模型与基础模型总声压级之差，负值表示总声压级降低，正值表示总声压级升高。可以看到，在500 Hz 以下中低频段，这9 个监测点中，模型A、B、C 总声压级分别降低了3.0、4.6 和4.3 dB；在20～104Hz 范围内，模型A、B、C 总声压级分别降低了1.9、3.3 和3.7 dB。

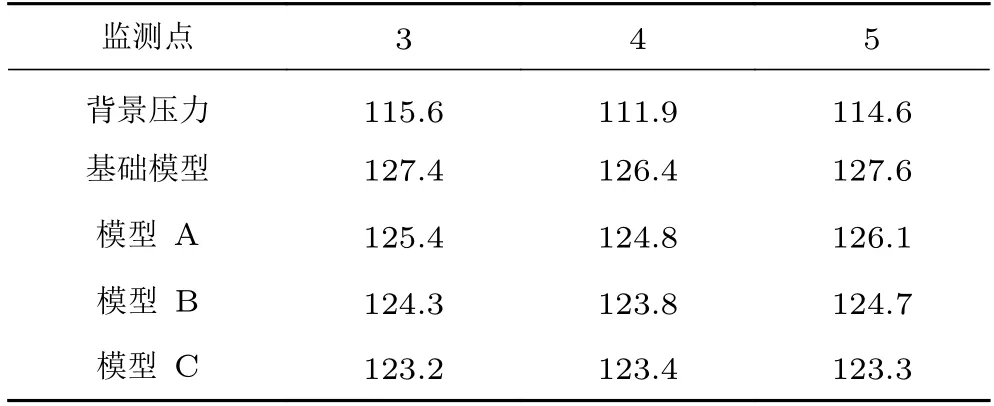
表1 第一排3 个监测点总声压级对照表Table 1 Comparison table of overall sound pressure level of three monitoring points in the first row单位：dB

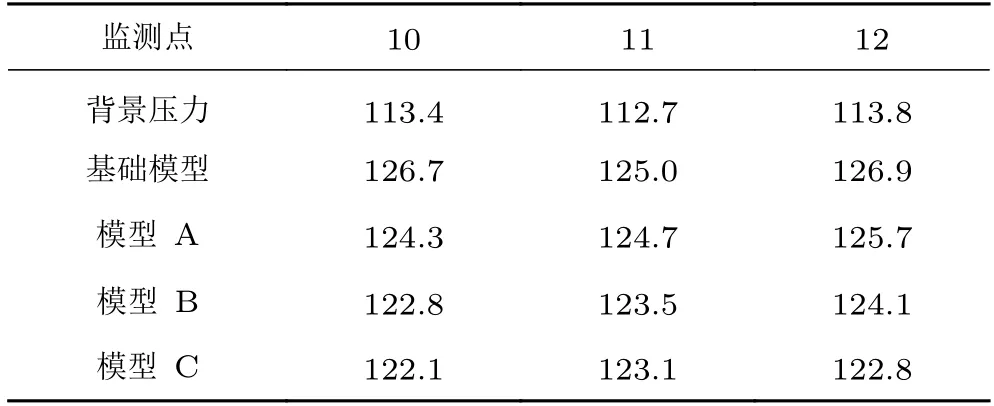
表2 第二排3 个监测点总声压级对照表Table 2 Comparison table of overall sound pressure level of three monitoring points in the second row单位：dB

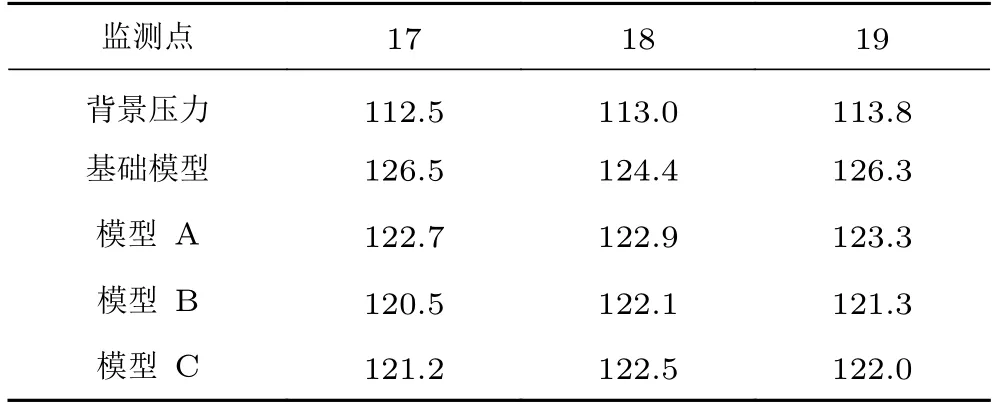
表3 第三排3 个监测点总声压级对照表Table 3 Comparison table of overall sound pressure level of three monitoring points in the third row单位：dB

表4 各改进模型与基础模型总声压级在不同频率范围内的差值Table 4 Overall sound pressure level differences between the modified models and the generic simple model单位：dB

2.2 流场特性

2.2.1 均匀流场

汽车侧窗脉动压力是产生气动噪声的主要原因之一，而外后视镜尾部的涡流场又是造成侧窗脉动压力的重要因素之一。在对尾涡流场进行PIV 测量时，每个工况拍摄了200 张图片，然后对其进行平均处理，再将平均后的结果导入Tecplot 后处理软件进行后续分析。在均匀流场中，所有模型在同一对比截面上的流线数目相同。

图14 为4 款不同造型外后视镜纵截面的流线对比图，图中为x 方向平均速度。从图中可以明显看出：在所有外后视镜模型下游都存在2 个方向相反的旋涡。其中，基础模型下方的旋涡尺寸较小，靠近后视镜模型，且紧贴平板壁面，脱落的旋涡拍打在壁面上可能产生比较强烈的壁面脉动压力，从而产生较大噪声。模型A 和C 的上下旋涡大小基本一致，模型B 下部旋涡远大于上部旋涡。相较于基础模型的旋涡中心，模型B 和C 的下部旋涡中心离平板壁面更远，且下部靠近平板壁面区域的平均速度明显大于基础模型该区域的平均速度。模型B 和C 平均速度为正值，即沿流向方向，而基础模型下部的速度都为负值，即整个为回流区。

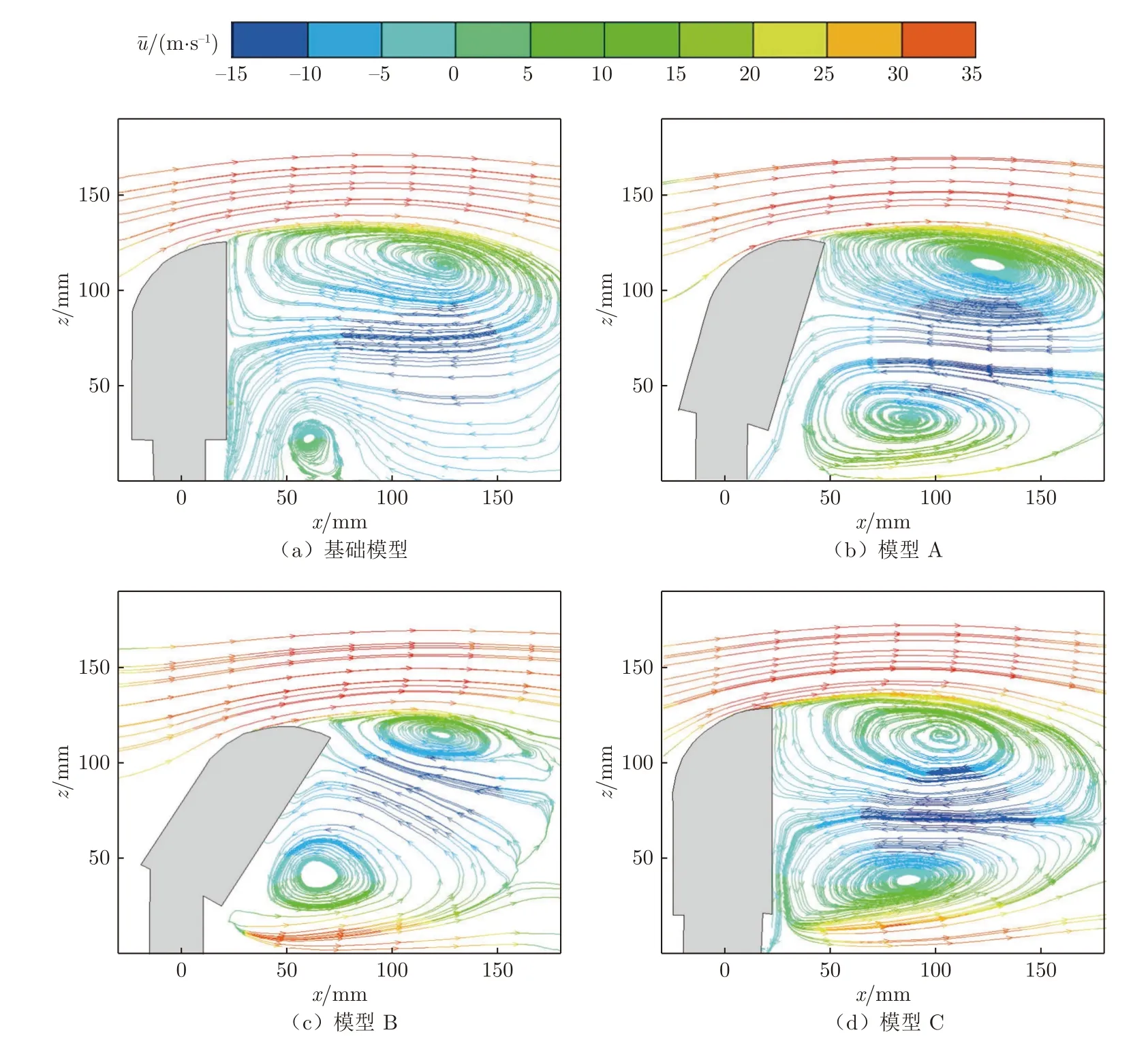
图14 纵截面流线对比图Fig.14 Comparison of streamlines in longitudinal section

图15 为4 款不同造型外后视镜横截面1 的平均速度流线对比图，由于激光不能透过外后视镜，因此外后视镜背光区存在一个没有流线的盲区。从图中可以看出：基础模型下游存在2 个流线密集且相互靠近的比较大的旋涡中心；3 个造型改进模型下游的旋涡明显减小，模型A 和C 的2 个旋涡互相远离，模型B 的2 个旋涡中心最小且流线最稀疏，说明这些改进均有利于减小旋涡对壁面的脉动压力，从而降低气动噪声。

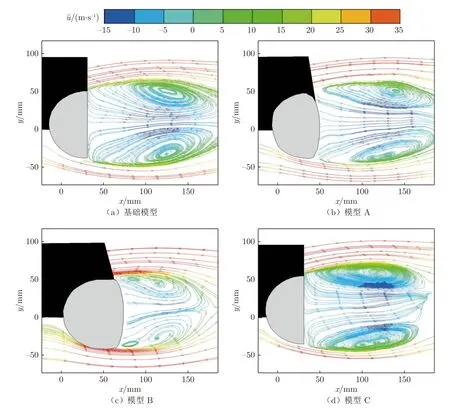
图15 横截面1 流线对比图Fig.15 Comparison of streamlines in cross section 1

图16 为4 款不同造型外后视镜横截面2 处的流线对比图。从图中可以看出：在基础模型下游不仅存在2 个范围较大的旋涡，且在其下游100 mm 处仍有回流区域的存在，说明旋涡扩散范围很大。截面2 靠近平板，扩散的旋涡将会在平板较大面积内产生剧烈的压力波动，从而产生明显的气动噪声，但相对于基础模型，其他3 款外后视镜模型都仅存在一对较小的旋涡，其中模型B 和C 的旋涡影响区域仅在模型下游40 mm 范围内，不易产生较高的气动噪声。

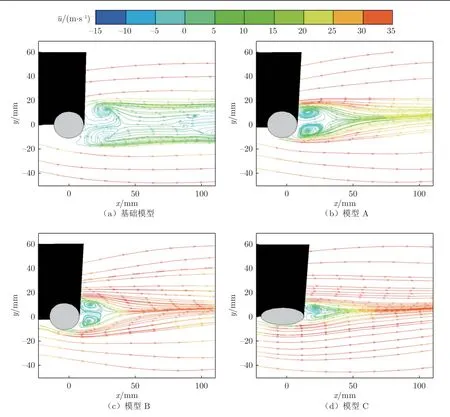
图16 横截面2 流线对比图Fig.16 Comparison of streamlines in cross section 2

综上所述，外后视镜造型对其尾迹区域流线和涡团分布有很大影响。相较于基础模型，3 款造型的改进使得靠近壁面的湍流涡影响范围大幅减小且远离壁面，这可能是各造型改进模型气动噪声降低的主要原因。

2.2.2 涡量分析

为进一步分析3 款造型改进模型的流场与降噪机理，对上述3 个截面进行瞬态涡量分析。

对应纵向截面，涡量 Ωy计算公式为：

式中，u 为x 轴瞬时速度，w为z 轴瞬时速度。

对应横向截面1 和2，涡量 Ωz计算公式为：

式中，v为y 轴瞬时速度。

图17 为4 个模型纵截面上的瞬时涡量场和矢量场分布对比图。从图中可以看出，在外后视镜下游存在一正一负2 种涡，上部顺时针旋转的负涡整体呈细条状，而下部逆时针旋转的正涡则呈零散分布状。观察图16 可以发现，基础模型的尾流呈现为破碎的小涡结构（碎涡），下部的碎涡直接拍打在壁面，将产生较大噪声；3 个改进模型尾流的涡结构与基础模型类似，都是碎涡结构，与频谱分析中的宽频特性对应。为了更好地评估不同造型外后视镜尾流对侧窗的脉动影响，下面再对横截面1、2 上的涡强分布进行分析。

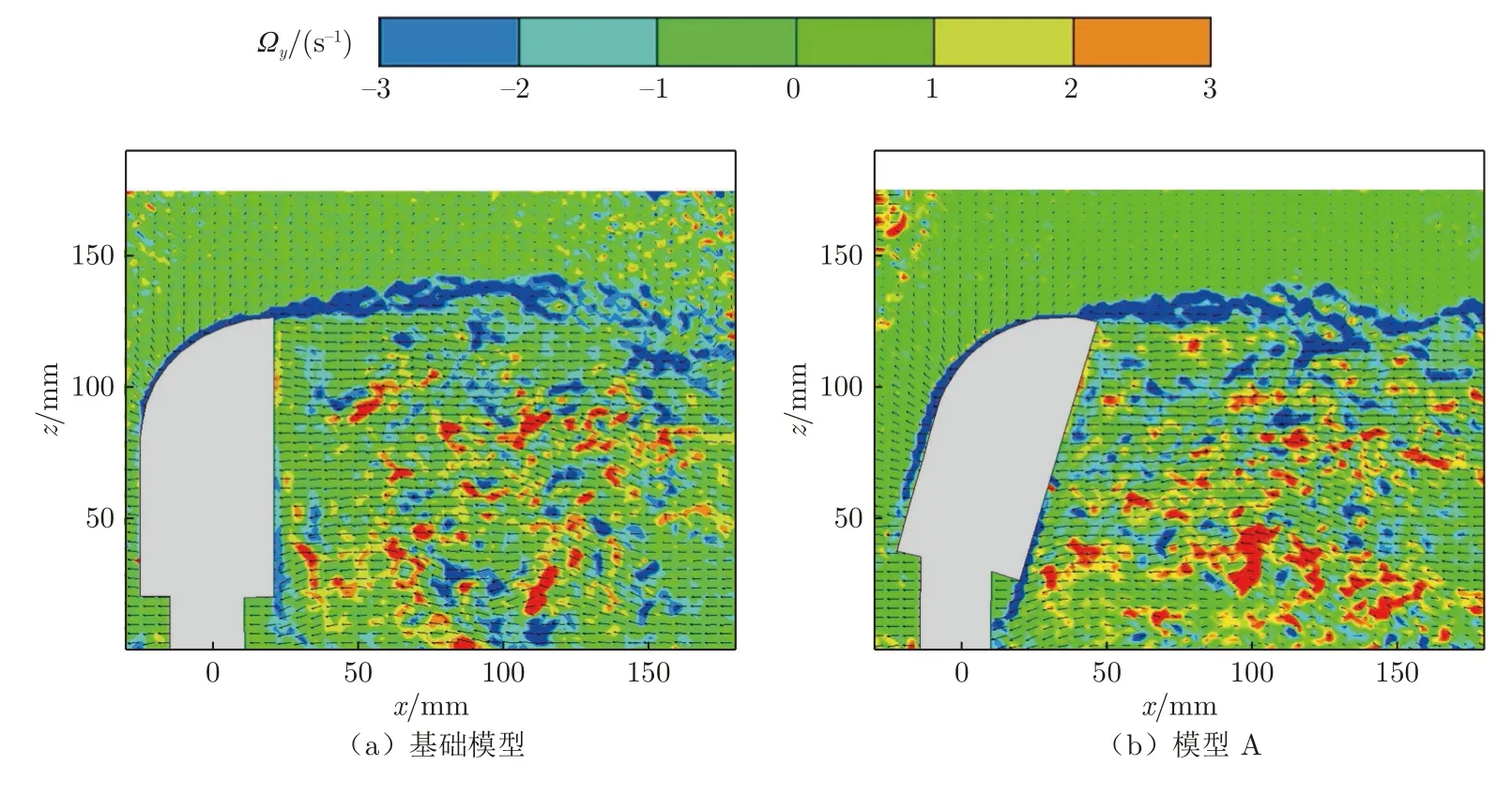
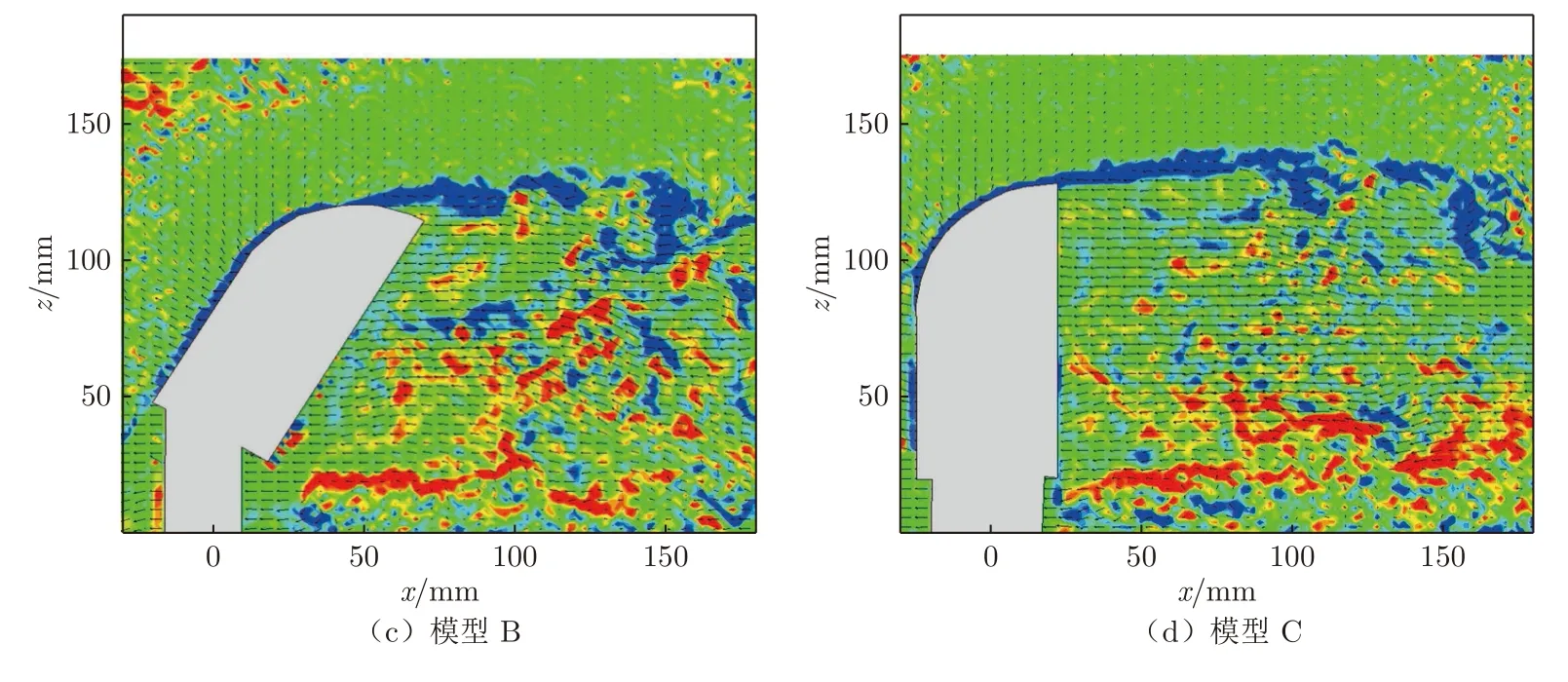
图17 纵截面涡强及矢量场分布对比图Fig.17 Comparison of vortex intensity and vector field distribution in longitudinal section

图18 为4 个模型横截面1 上的涡强及矢量场分布对比图。从图中可以看出，相较于其他模型，基础模型的旋涡扩散范围最大，不仅存在2 个较大的呈细条状的正负旋涡，还存在大量混合的旋转方向相反的正负碎涡。在该截面上，所有模型下游均出现破碎的旋涡，但碎涡特性变化不明显。

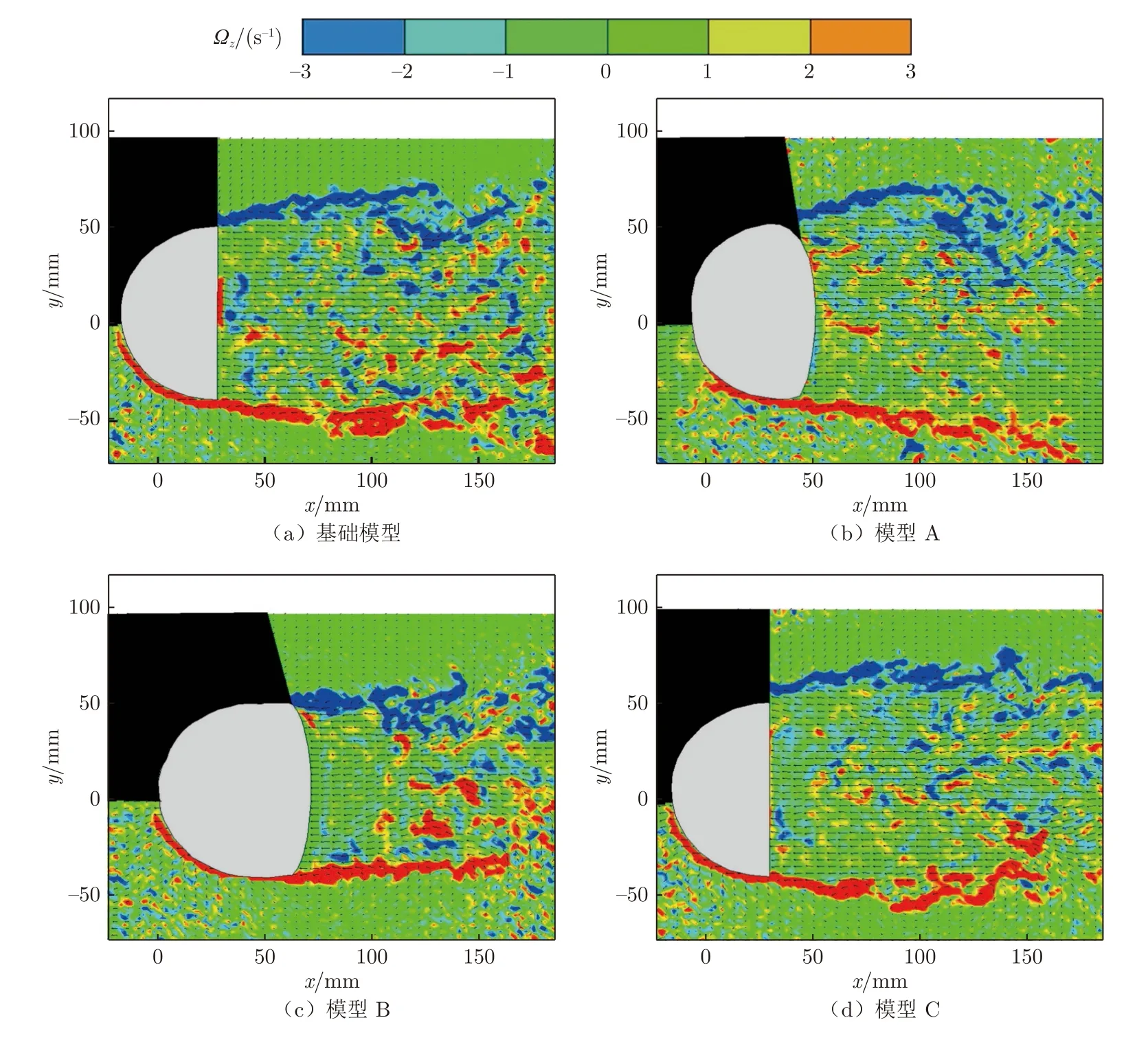
图18 横截面1 涡强及矢量场分布对比图Fig.18 Comparison of vortex intensity and vector field distribution in cross section 1

图19 为4 款模型横截面2 上的涡强及矢量场分布对比图。横截面2 靠近壁面，其涡量分布会对壁面脉动压力产生很大影响。从图中可以看出：基础模型下游存在2 个扩散范围很大的正负旋涡，改进外后视镜造型后，模型下游2 个涡团扩散范围都大幅度降低，即外后视镜偏转30°后（模型B），底部圆柱两侧尾流剪切层明显变短，使涡量更早注入到小尺度涡旋运动中。支撑柱为椭圆柱的模型（模型C）下游2 个旋涡扩散范围比基础模型小得多，是所有模型中最小的。

与一般二维圆柱尾流呈现卡门涡街不同，基础模型和模型A、B 的尾流下游都没有明显的周期性交替旋涡脱落，其尾流涡都是破碎的小尺度结构。模型C 的尾流呈现出一定的周期性旋涡脱落，这解释了为何模型C 的脉动压力频谱图中50～70 Hz 范围会出现一个频率波峰。

2.2.3 正反模态分解（POD）

横截面2 的流场特性更能反映尾流对侧窗壁面脉动压力的影响，对该截面获得的PIV 速度场序列进行正交模态分解。通过正交模态分解可以获得流场主要能量结构及各个模态所对应的能量比例[21]。图20 为经正交模态分解后，各模型在横截面2 上的第一模态信息。由图20 可知：对于基础模型和模型A、B，第一模态在流场中的结构较为分散，说明在该截面没有周期性脱落的大尺度旋涡；模型C 沿流向分布具有一定的类涡旋结构。为了更好地分析流场特征，对所有模型的第二模态也进行了分析，发现基础模型和模型A、B 的第二模态也呈发散分布，因此不再给出其对比分析图。图21 为模型C 的POD 第二模态，从图中可以看出：模型C 的第二模态具有比较明显的类涡旋结构，该结构对侧窗的湍流脉动可能产生影响，这也是模型C 的脉动压力频谱图中有一较明显波峰的原因。

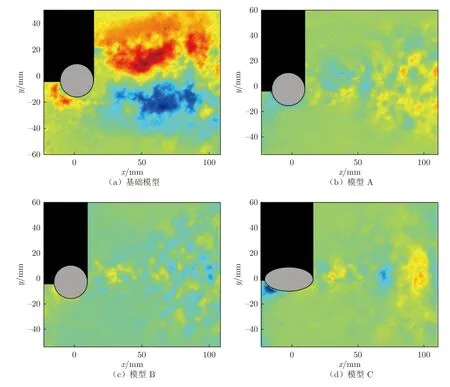
图20 横截面2 上POD 第一模态y 方向分布对比图Fig.20 Comparison of first POD mode （mode-1） associated with the vertical fluctuating for flows over four models

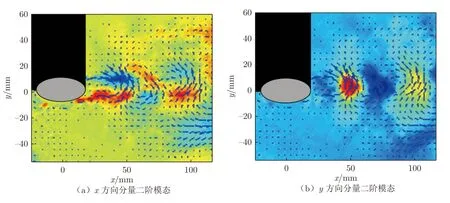
图21 模型C 横截面2 的POD 第二模态及矢量场分布对比图Fig.21 Second POD mode （mode-2） associated with the streamwise and vertical fluctuating for flows over model C

POD 不仅可以获得流场的模态信息，还可以得到流场模态的能量分布。图22 为4 款模型横截面2 的流场中前20 个模态的能量信息。从图中可以看出：基础模型POD 第一模态所占能量比例达到14.6%，大于模型A、B、C 所对应的能量比例（分别为12.5%、6%和11%），POD 第十模态以后的高阶模态的能量分布大致相同。在POD 方法中，若较低的模态具有较高的能量，则与较大尺度的结构对应；若较高模态具有较低的能量，则与较小尺度的结构对应。所有模型在前20 个模态的能量累积中，基础模型能量累积达61.7%，高于模型A、B、C 所对应的能量累积值（分别为54.2%、44.6%、54.6%）。

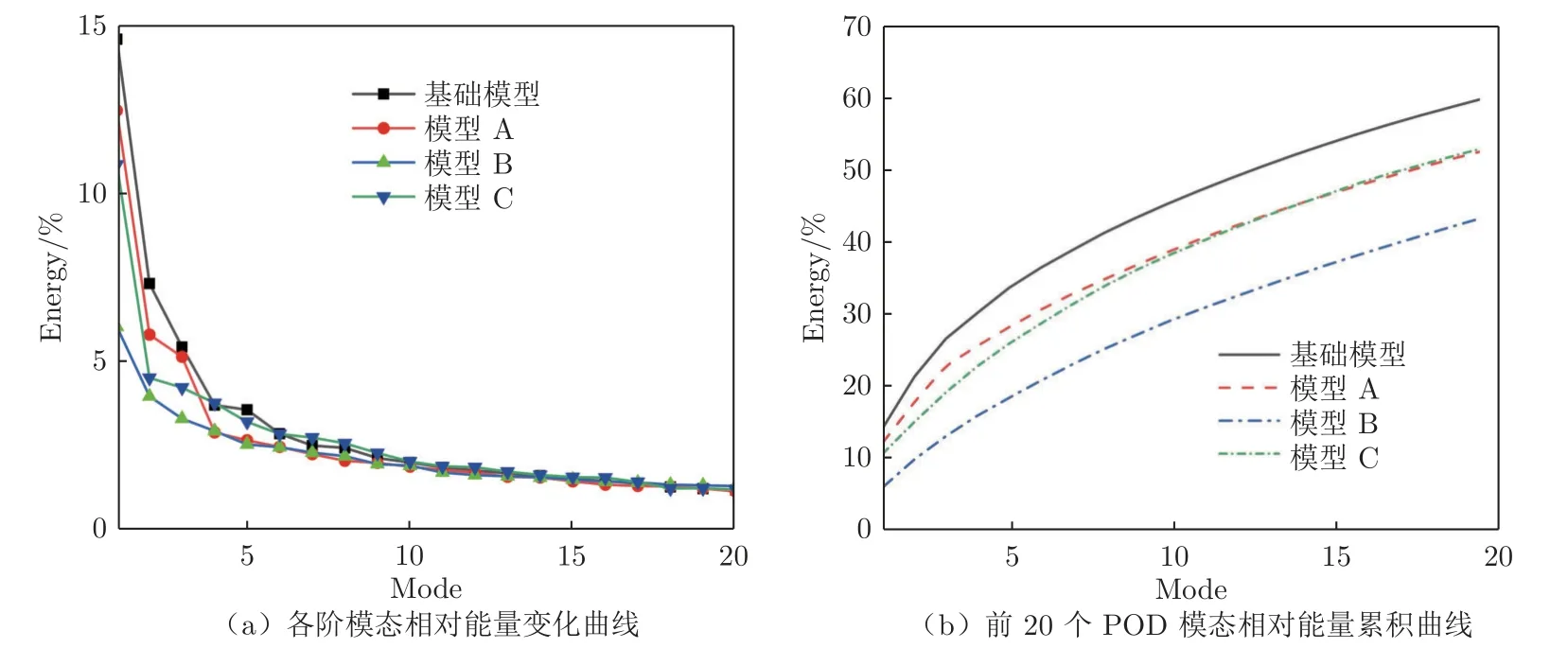
图22 4 个模型在横截面2 上的POD 模态动能百分比Fig.22 Percentage of kinetic energy held by the POD modes for the four models on the cross section-2

综上所述，改进模型A、B、C 的流场空间尺度变小，大尺度结构旋涡变成小尺度结构旋涡，总能量大幅降低，外后视镜对侧窗的壁面湍流脉动的影响减弱，从而有效降低了气动噪声。

2.3 阻力与阻力系数分析

表5 为动态天平对每个模型进行5 次测试后得到的阻力均值F（即模型阻力值）。相对误差δ的计算公式为：

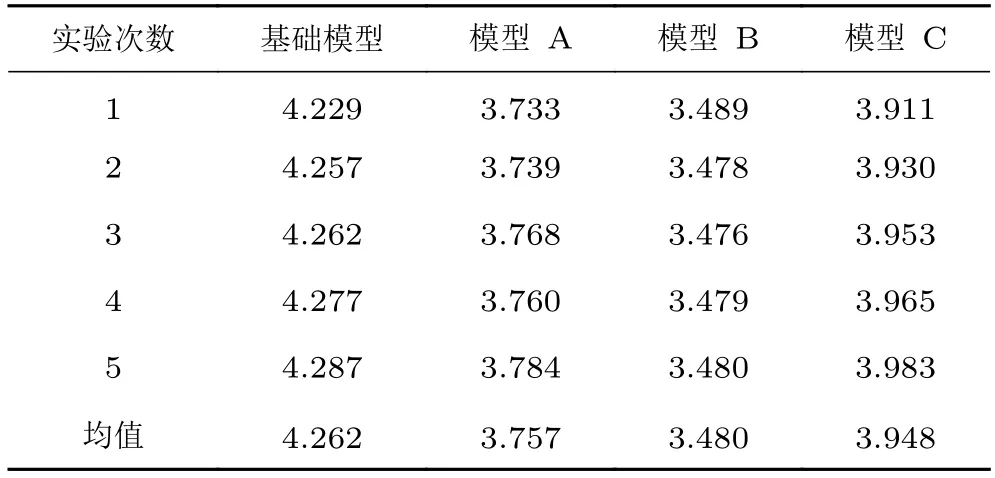
表5 模型阻力实验值Table 5 Test values of models drag单位：N

式中：F 为模型阻力，即5 次测试结果的均值；Fn为各模型不同测试次数时的阻力，下标n 代表测试次数。分析表4 中数据可知，每个模型5 次测试数据与其平均值的最大相对误差分别为0.77%、0.72%、0.26%和0.94%，均小于1%，说明本次实验是合理有效的。

图23 为不同模型阻力对比图。从图中可以看出，与基础模型相比，3 款造型改进模型阻力值均有所减小。在3 款造型改进模型中，模型B 阻力最小，模型C 阻力最大，模型A 介于两者之间。分析图中数据可知，与基础模型相比，模型A、B、C 的阻力分别降低了0.505、0.782 和0.314 N。

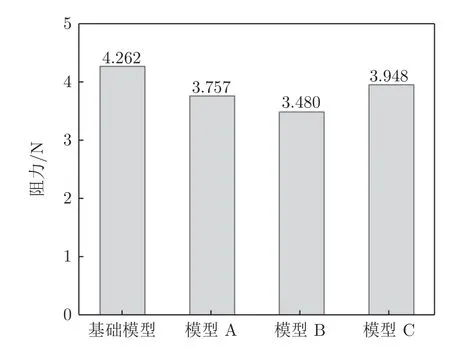
图23 不同模型阻力值Fig.23 The drag values of different models

图24 为基础模型及3 款造型改进模型的阻力系数对比图，阻力系数 CD计算公式为：

图24 不同模型阻力系数值Fig.24 The drag coefficient of different models

式中：ρ为空气密度，常温下取1.205 kg/m3；S为基础模型迎风面积，其值为9.331×10-3m2；来流速度U∞为33.3 m/s。分析图中数据可知，模型A、B、C 的迎风阻力系数比基础模型分别低11.8%、18.4%和7.5%。

3 结 论

本文对一简化汽车外后视镜模型及改进模型的流场、壁面脉动压力和迎风阻力进行了实验测量，研究发现：

1）对外后视镜外形进行合理改进，可以使外后视镜尾涡远离壁面，减小壁面脉动压力，降低气动噪声。

2）把外后视镜镜身偏转15°和30°，能明显降低模型气动阻力和壁面脉动压力，且偏转30°的效果优于偏转15°。当把外后视镜镜身偏转30°时，其阻力系数比基础模型降低18.4%，9 个壁面脉动压力监测点的总声压级在中低频段平均降低4.6 dB。

3）外后视镜底部支撑柱形状对外后视镜整体的气动特性影响较大，当把其圆柱形状改为本文研究的椭圆柱形状时，阻力系数降低了7.5%，9 个壁面脉动压力监测点的总声压级在20～500 Hz 频段平均降低了4.3 dB。