真空管道列车流固耦合研究进展及关键技术分析

寇杰，符澄，高兴龙，孙运强

中国空气动力研究与发展中心 设备设计与测试技术研究所，绵阳 621000

0 引 言

作为一种新型轨道交通工具，磁浮列车不存在传统列车的轮轨黏着限制、轮轨摩擦阻力等问题，理论上可以实现更高速度的商业运行，近年来受到越来越多研究者的关注，已经成为轨道交通领域的热点研究对象[1-2]。

磁浮列车依靠悬浮力运行，与运行轨道间有一定间隙，高速运行时存在明显的地面效应；同时，高速磁浮列车运行的目标速度为600～1 000 km/h（图1 为我国正在研发的600 km/h 速度等级高速磁浮列车），远高于现有高速列车。高速运行条件下的气动阻力等气动载荷更大，对磁浮列车的外形、结构及控制系统设计都带来了巨大挑战[3]。为实现磁浮列车高速运行，研究者提出了真空管道列车概念，其中以2013 年埃隆·马斯克提出的Hyperloop 胶囊列车最为著名[4-5]。真空管道列车的原理是通过抽吸空气实现封闭管道内部的低压状态，降低磁浮列车周围流场空气密度，从而大幅降低列车运行中的气动阻力，实现超高速运行[6]。

图1 600 km/h 速度等级磁浮列车[1]Fig.1 The maglev train at speed of 600 km/h [1]

低压环境及管道的封闭边界条件，给真空管道列车带来了一系列气动问题。列车在管道内超高速运动，其前方形成压缩波，后方产生膨胀波[7]；压缩波和膨胀波在管道内传播，进一步形成各种斜激波；各种激波反射叠加，引起管道内压力波动；再叠加车头、车身和车尾通过时的压力扰动，整个管道内的流场环境十分复杂。真空管道列车前方和后方产生的压缩波包括斜激波、正激波、反射激波、Lamda 激波、菱形激波等复杂的激波簇结构，这些复杂结构与列车相互作用，形成高度非稳定的列车运行环境[8-9]。悬浮运行的真空管道列车和管道之间存在明显间隙，列车运行中的不稳定将导致流场环境边界条件发生变化，进一步影响真空管道内部流场。因此，真空管道列车周围的气体压力和速度均受到列车速度和姿态的影响，存在严重的流固耦合效应。

本文对真空管道列车气动研究进展及轨道列车流固耦合特性研究进展等进行了综述，分析了真空管道列车流固耦合关键技术，并对下一步研究提出了建议。

1 真空管道列车气动研究进展

1.1 真空管道列车气动特性

采用真空管道的目的是降低列车运行中的气动阻力，真空管道列车的气动阻力特性是研究者重点关注的问题。周晓等[10]建立了二维不可压缩真空管道列车数值计算模型，研究了真空管道气体压力、阻塞比、列车速度对气动阻力的影响，发现阻塞比增大会导致列车气动阻力急剧增大，管道内部压力降低则会降低气动阻力，表明真空环境对于列车高速运行具有基础性作用。Kim 等[11]采用相似方法开展研究，得出的真空管道列车气动阻力与列车速度、阻塞比和管道压力的关系与周晓等的研究具有较好的一致性；Kim 等还关注了真空管道列车前方产生激波的临界速度，该速度主要与阻塞比相关。刘加利等[12-13]将真空管道列车数值计算模型拓展至三维，建立了3 节车列车模型和真空管道内部流场的三维计算模型，如图2 所示。

图2 真空管道列车三维计算模型[12]Fig.2 A three-dimensional calculation model for a vacuum pipe train[12]

该研究将列车气动阻力D 分为两部分，即压差阻力Dp和摩擦阻力Dτ。为分析各阻力的关系，定义了无量纲的气动阻力系数CD、压差阻力系数CDp和摩擦阻力系数CDτ：

研究发现，在不同运行状态下，摩擦阻力系数CDτ均远小于压差阻力系数CDp，因此，压差阻力对列车气动阻力起决定性作用。从图3 和4 可以看出，当管道压力和列车速度固定时，气动阻力随阻塞比增大而增大。低压条件下，列车速度和管道压力对列车压差阻力和气动阻力基本无影响，而阻塞比则对气动阻力影响明显。

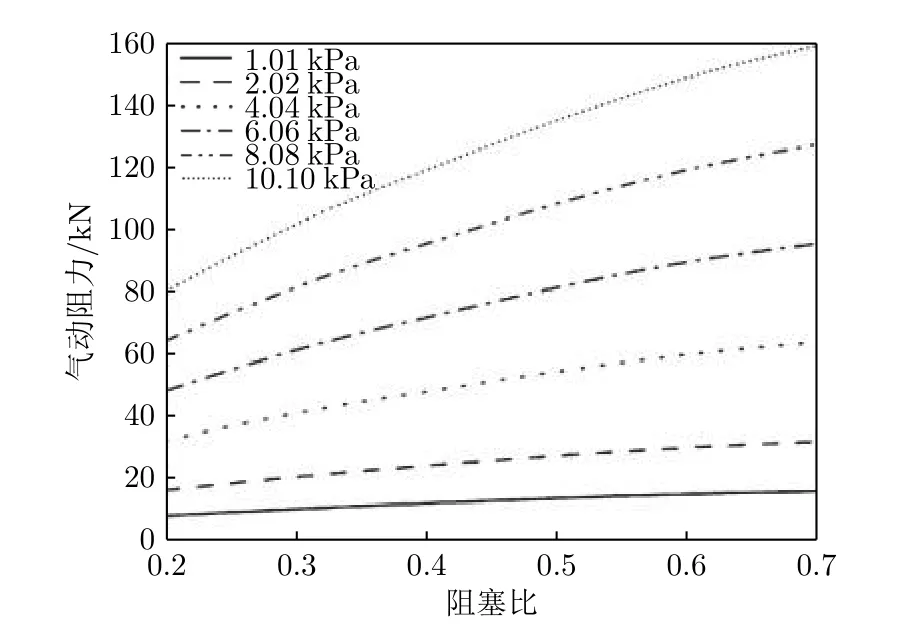
图3 不同管道压力下气动阻力随阻塞比的变化[12]Fig.3 Aerodynamic drag changes with the blockage under different pipeline pressures[12]

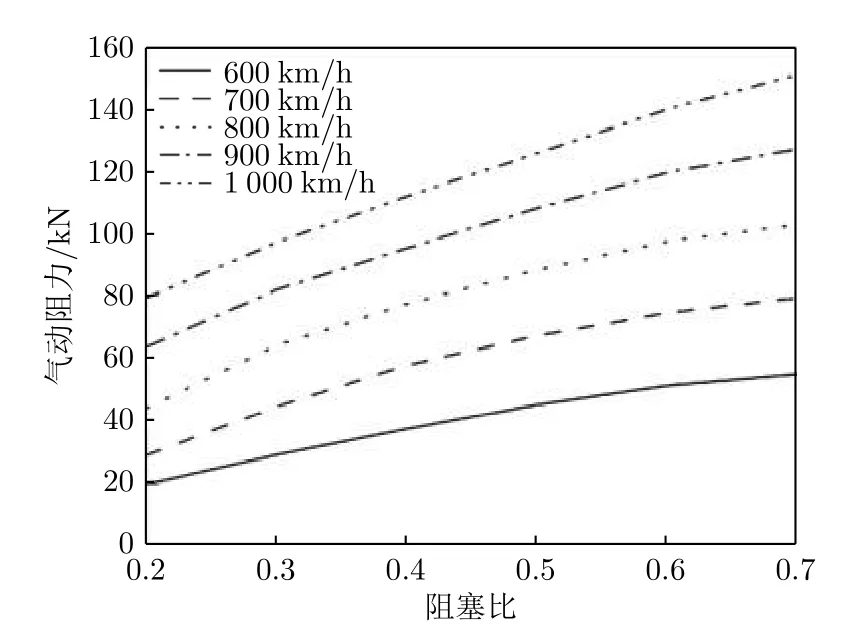
图4 不同列车速度下气动阻力随阻塞比的变化[12]Fig.4 Aerodynamic drag changes with the blockage under different speeds[12]

在真空管道列车气动载荷特性研究方面，王博[14]采用三维数值仿真与模型试验方法对真空管道高温超导磁浮列车气动阻力与管道压力、列车速度、阻塞比的关系进行了研究，提出了一种低压惯性试验方法。黄尊地等[15]依据最小空间尺寸计算克努森数，判断真空管道内的流动状态，考虑三维定常可压缩效应，利用滑移网格技术，分析列车速度、管道真空度、阻塞比及环境温度对列车气动阻力的影响。王志飞等[16]提出了一种基于数值仿真和正交理论相结合的参数设计研究方法，分析了影响真空管道列车运行的3 种因素（列车速度、阻塞比和管道压力）对列车气动阻力的影响趋势及各因素影响的显著性。冯瑞龙等[17]基于RBF（Radial Basis Function）和BP 神经网络（Back Propagation Network），训练了一种真空管道列车气动阻力预测模型，分析了阻塞比、列车速度和管道压力影响下的气动阻力。

陈绪勇[18-19]和Zhang[20]等则关注了不同头车外形对真空管道列车气动阻力的影响，建立了二维计算模型，对不同头车外形的真空管道列车气动阻力进行数值分析。Pandey 等[21]分析了头车外形与尾车外形对真空管道列车气动阻力的影响，如图5 和6 所示，不同的头车和尾车流线型设计对车头和车尾的气压差影响有限，因而对列车压差阻力影响较小。Yang 等[22]也研究了头车外形和尾车外形对真空管道列车气动阻力的影响，并在研究中加入了管道压力、列车速度等影响因素。Zhang[23]研究了真空管道直径和阻塞比对列车气动阻力的影响，研究结果显示对于半径1.5 m 的真空管道列车，最佳管道直径为2～4 m。Bi 等[24]构建了一段550 m 的封闭管道，研究发现真空管道列车的气动阻力在激波和反射波共同作用下是一个时变量，且受到激波传播的时间影响，如图7 所示（图中α 为阻塞度、β 为管道内气压与标准大气压比值、vt为列车运行速度）。Ma 等[25]建立了真空管道列车气动阻力与阻塞比、列车速度和管道压力之间的理论模型，并采用试验装置（图8）获得的数据进行了验证，但该研究仅针对真空管道列车低速运行开展，且理论分析结果与试验结果差异明显。

图5 不同头车形状条件下的气压差[19]Fig.5 Pressure differentials under different header shapes[19]

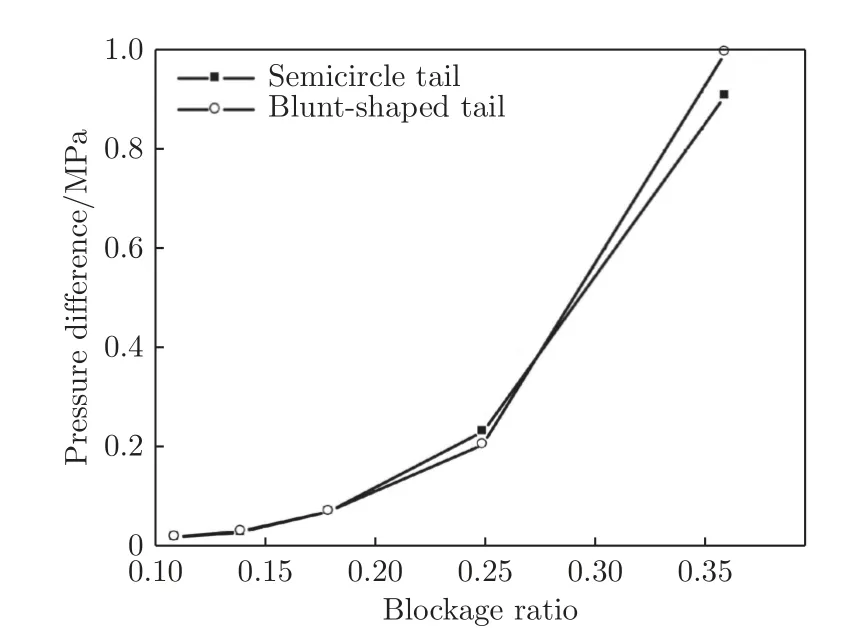
图6 不同尾车形状条件下的气压差[19]Fig.6 Pressure differentials under different trailer shapes[19]

图7 封闭管道内气动阻力时域变化曲线[24]Fig.7 A change curve of the aerodynamic drag within the closed pipe[24]

图8 真空管道列车试验装置[25]Fig.8 Vacuum pipe train test device[25]

从现有研究可以看出，真空管道列车气动阻力主要与列车速度、阻塞比、管道压力和列车外形等因素有关。管道内气体的阻塞效应对列车气动阻力系数起决定性作用，需在真空管道列车气动设计中重点考虑管道的阻塞比[26-28]。真空管道列车实际运行中，在管道内还可能受到升力、横向气动力和气动力矩的影响，但现有气动载荷特性研究基本局限于气动阻力研究，尚未对其他气动载荷给予充分关注。

1.2 真空管道列车流场特性

列车在具有一定真空度的封闭管道内运行，带动管道内气体流动，在列车周围形成一定的气压波。管道内存在压缩波、膨胀波及各类斜激波组成的复杂波系[29]，严重影响真空管道列车运行的稳定性和安全性，同时还是管道壁面承载压力的主要影响因素。因此，对真空管道内各种压力波的产生、传播及演变问题应给予关注。

真空管道列车压力波的产生机制和传播机理复杂。张晓涵等[30]建立了二维亚声速真空管道列车模型，采用数值计算方法研究了真空管道列车运行前方气动壅塞现象与后方非对称尾部激波现象。图9为不同列车速度下真空管道气动壅塞特性的对比（图中，Ma0、Mat分别为来流马赫数、管道喉道马赫数，m0和m1分别为列车-管道前方自由空间的空气流量、自由来流进入列车-管道之间的空气流量）。列车低速运行时，真空管道内未发生壅塞现象；亚声速运行时，管道内发生临界壅塞现象，列车顶部出现马赫数为1 的临界点（即“等熵极限”）；在高亚声速、超声速运行时，管道内持续保持雍塞，列车后方产生弓形激波，影响列车后方的气体流动。

图9 真空管道内部等熵流动流场特征分析[30]Fig.9 Analysis of flow field characteristics of isentropic flow in vacuum pipe[30]

列车在高亚声速和超声速运行时，其头部前方出现了由溢出气流堆积而成的高压区。通过计算，可以拟合出列车前方的雍塞长度和列车运行时间的关系：

式中：L 为列车前方壅塞长度，t 为列车运行时间，Ma 为列车运行马赫数。

图10 为600 km/h 运行速度下真空管道列车尾部区域的马赫数分布。此时真空管道列车尾部区域存在膨胀波和激波。当来流为高亚声速时，尾部形成局部超声速区域，诱发产生一系列膨胀波，膨胀波经过尾部流线型、管道上表面的多次反射与叠加，形成了较短的激波。激波在管道上表面边界层中与剪切层相互作用，导致列车上方和管道内壁之间激波反射不稳定，产生激波串并向后耗散。

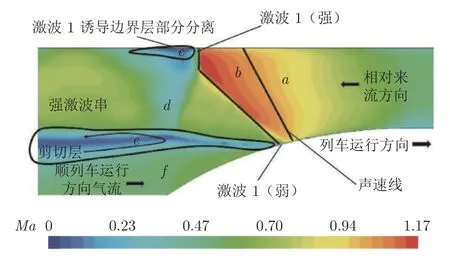
图10 600 km/h 运行速度下列车尾部马赫数分布[30]Fig.10 Mach number distribution at train trail at speed of 600 km/h[30]

Oh[31]、Gillani[32]、Kang[33]、Zhou[34]和Bao[35]等采用稳态分析方法研究了压力波与列车运行速度、列车长度、管道压力、管道温度和阻塞率的关系。列车实际运行产生的压力波并非完全稳定，其前方压缩波、后方膨胀波及激波的传播与反射叠加，以及管道的壁面效应，使压力波呈现非稳态[36]。Kim 等[11]将真空管道列车后方斜激波的产生和传播机理作为非稳态问题进行研究，Niu[37]、Sui[38]和Yang[22]等也采用非稳态二维数值模拟方法研究了斜激波与列车速度、管道压力、阻塞率等的关系。Niu 等[39]还利用非稳态数值模拟方法研究了列车加速和减速过程中斜激波的特性。Sui[38]和Bi[24]等则研究了压力波和膨胀波的产生和传播机理。周鹏等[8]研究了真空管道列车超高速运行中产生的各类波系（图11 和12 展示了弓形激波、正激波、反射激波、Lamda 激波、菱形激波等激波簇结构的产生和传播特性。图中，P1、P2、P3 分别为激波的反射位置1～3；R2、R3 为反射波2 和3；I1 为弓形激波1；N 为正激波；M3 为马赫杆3），研究结果表明，真空管道内的各类激波使列车气动环境比运行于开放流场的普通高速列车更为复杂，且各类激波的传播、反射相互叠加，使列车运行流场环境具有高度的非稳定性。

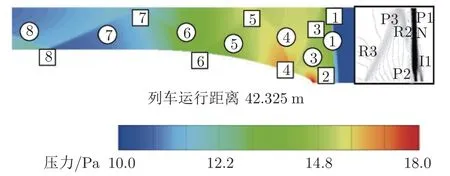
图11 车头处压力云图和激波结构图[8]Fig.11 Pressure clouds and shock cluster structure maps at the head of the vehicle[8]

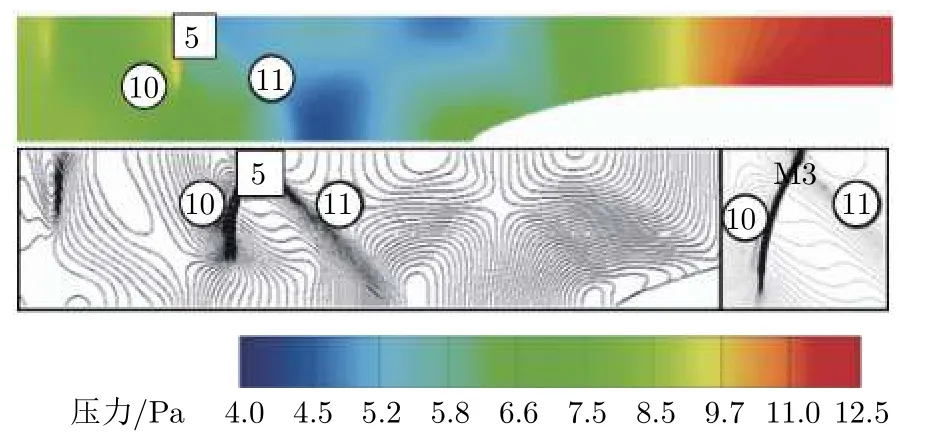
图12 车尾处压力云图和激波结构图[8]Fig.12 Pressure clouds and shock cluster structure maps at the end of the vehicle[8]

不稳定的激波簇结构对真空管道列车产生时变气动载荷，在时变气动升力、气动力矩及其他各种带有冲击性的气动载荷作用下，列车运行特性必将发生变化。因此，对真空管道列车气动阻力之外的气动载荷也亟待开展深入研究。

2 轨道列车流固耦合研究进展

作为流体力学和固体力学相互耦合发展出的力学分支，流固耦合研究在机翼颤振、油箱内燃油晃动和高层建筑风载变形等实际工程问题中均体现出重要价值。传统流固耦合研究主要研究流场和固体场相互作用的结果，在数值计算方法方面，需要研究两种场的交界面上的各种物理参数的平衡与协调。轨道列车的流固耦合研究属于流体力学和多体动力学耦合的交叉学科研究，与传统流固耦合研究重点关注的流体力学和固体力学耦合差别较大，但这种交叉学科研究在轨道交通研究领域仍被称为“流固耦合研究”。

真空管道列车与传统轨道列车具有一定的相似性，其流固耦合研究可以借鉴轨道列车流固耦合研究的分析方法、分析手段并参考相关分析结果。

2.1 轨道列车流固耦合分析方法

轨道列车流固耦合研究重点关注外界环境风作用下的列车运行状态。于梦阁[40-41]、Bettle[42]、王永冠[43]、Baker[44]、Thomas[45]、李田[46]等利用气动计算软件或理论模型分析得到了外界环境风作用下高速列车受到的气动载荷，进而采用车辆动力学计算软件分析了气动载荷作用下高速列车的运动特性。该离线方法可以快速计算高速列车气动载荷及动力学指标，但并未考虑气动载荷导致的列车运行姿态变化及变化的列车运行姿态对流场特性产生的影响。

杨吉忠等[47]采用有限体积法和任意拉格朗日欧拉法（Arbitrary Lagrangian Eulerian,ALE）进行了气动计算和车辆动力学计算的耦合分析。与之类似，为分析侧风作用下的列车动力学特性，崔涛基于ALE 及车辆动力学模型对比分析了流固耦合效应对车辆气动力和气动力矩的影响，发现在列车气动分析中考虑列车运行姿态变化和列车流固耦合效应，会对车体摇头力矩（侧向力不作用于质心时产生的力矩）产生明显影响。崔涛等[48]建立了列车流体动力学模型，并采用参数传递、求解控制和动态网格技术将气动载荷参数从流体动力学模型传递至车辆动力学模型，还提出针对不同问题可以采用不同耦合方法联立流场方程和车辆动力学方程。联立耦合方法可分为离线耦合、显式耦合和隐式耦合：离线耦合仅在车辆动力学计算中引入气动载荷；显式耦合利用车辆系统响应子模块与气动子模块相互交换数据实现实时交互求解；与前两者相比，隐式耦合选择性地进行数据交互，需在车辆系统响应子模块和气动子模块都达到稳定状态的前提下进行数据交互。

李田等[49-52]构建了基于气动软件Fluent 和车辆动力学软件Simpack 的联合仿真模型。如图13 所示，利用一个接口程序将Fluent 和Simpack 相互连接，以Fluent 计算得到气动载荷，经接口程序传递至Simpack，以Simpack 计算列车在气动载荷下的运行姿态和运动参数，并将相关参数经接口程序传递至Fluent，Fluent 根据更新的输入参数进行新一步计算。

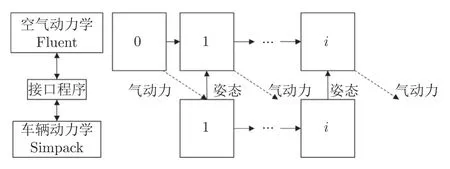
图13 联合仿真求解过程Fig.13 Joint simulation resolution process

在车辆-轨道耦合动力学方程中引入2 个积分参数（μ和λ），用以构造新的显式积分格式：

式中：Xn-1、Xn和Xn+1分别表示第n-1、n 和n +1 个迭代步的位移矩阵；Δt 为时间积分步长。

基于Fluent 和Simpack 的流固耦合计算需经接口程序实现两者之间的数据交换，其中一个程序的计算过程中，另一程序基本处于等待参数的状态；同时，气动计算和车辆动力学计算的时间步长存在数量级差异，导致后者等待时间较长，严重影响计算效率。此外，由于是给定时间步长进行迭代，气动计算比车辆动力学计算的迭代步长更长，导致气动计算得到的气动载荷在2 个输出的迭代步之间变化较大，可能导致车辆动力学计算在突变气动载荷输入下不收敛。

针对联合仿真的计算效率和计算收敛问题，李田[53]提出了一种内嵌式高速列车流固耦合联合仿真方法，如图14 所示。

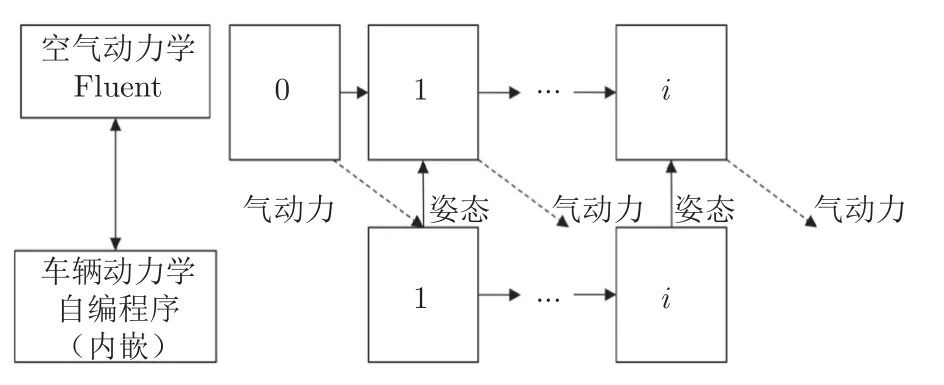
图14 内嵌式联合仿真求解过程Fig.14 Embedded joint simulation resolution process

该方法改进了车辆动力学计算部分，通过编程将车辆动力学计算程序包内嵌至气动计算软件，无需借助接口程序进行数据传递，在气动计算软件中即可实现气动计算和车辆动力学计算，避免车辆动力学计算因缺乏输入长期处于等待状态，大幅提高了联合计算效率。同时，为降低突变气动载荷对计算收敛性的影响，在车辆动力学计算程序中线性插值当前时刻和上一时刻的气动载荷，使得加载的气动载荷连续。t 时刻作用于列车-轨道耦合动力学模型的气动载荷Fa表达式为：

式中：tn、tn+1分别为第n 个和第n + 1 个迭代步时间；Fn、Fn+1分别为tn、tn+1时刻Fluent 计算得到的气动载荷。

在常值的横风作用下，列车的气动状态和车辆动力学状态会达到稳定。基于此原理，李田等[54]提出了一种新的流固耦合计算方法—平衡状态法，用以快速计算横风作用下的高速列车流固耦合特性。在计算中，为判定计算的气动力是否达到稳定状态，对每一项指标设置一定的收敛判断准则：

式中：Fn和Fn+1分别为第n 个和第n + 1 个迭代步的气动力指标值；ε 为收敛误差，取ε=0.001。

在平衡状态法中，首先需计算初始状态下高速列车的稳态流场，并对计算得到的气动载荷进行收敛性判定，若达到收敛状态则将气动载荷输入车辆动力学计算程序，计算气动载荷作用下的列车姿态参数，并根据姿态参数更新气动计算的网格数据，作新一步气动计算后再次输出气动载荷数据，如是循环，直至气动计算结果和车辆动力学计算结果均达到收敛，则表明计算进入平衡状态，即可输出车辆动力学和气动计算结果。如图15 所示。

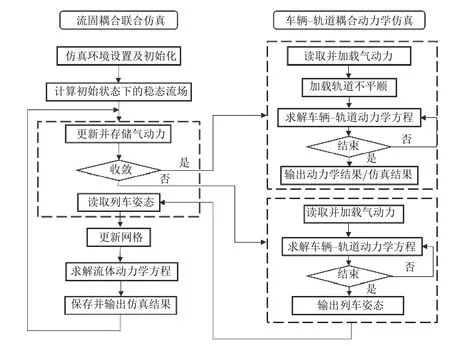
图15 平衡状态法联合仿真求解过程[54]Fig.15 Joint simulation resolution process in balanced state method[54]

根据李田的研究，可以得到如表1 所示的3 种流固耦合方法计算效率的对比。离线仿真法的气动计算总迭代步数和动力学计算总时间均最少，但存在前文所述的准确性和收敛性问题，难以反映实际的流固耦合特性。对比平衡状态法和交互式联合仿真法可以发现，前者气动计算每个时间步的迭代步数（100 步）多于后者（20 步），但前者的时间迭代总步数（50 步）远少于后者（7 500 步）。由于平衡状态法每次迭代均需使用动力学计算，其动力学计算总时间比交互式联合仿真法多250 s，但在整个流固耦合仿真过程中，气动计算所需时间远多于动力学计算，因此平衡状态法计算效率更高。

表1 计算效率比较[54]Table 1 The contrast of computational efficiency[54]

在目前的轨道列车流固耦合计算方法研究中，李田等的研究成果兼顾了计算精度和计算效率，具有较好的创新性和实用性；提出的联合仿真法、内嵌式联合仿真法、平衡状态法均可作为真空管道列车流固耦合研究的参考和借鉴（在研究中，仍需考虑真空管道列车流固耦合研究的特殊性）。

2.2 流固耦合作用下的列车运行特性

在流固耦合作用下，列车的动力学性能受到气动载荷的激励发生明显改变。为准确计算气动载荷作用下的列车运行特性，研究者采用流固耦合计算方法将气动计算和车辆动力学计算联系起来，相关研究包括了第2.1 节提及的离线式流固耦合计算和交互式流固耦合计算。

表2 和3 分别为采用不同流固耦合计算方法得到的列车气动载荷指标和运行姿态指标[54]。从表中可以看出：平衡状态法和交互式联合仿真法得到的结果差异相对较小；离线仿真法得到的气动载荷指标和运行姿态指标与其他2 种方法差异明显。离线仿真法得到的结果不够准确，难以体现真实的列车流固耦合特性。

表2 气动载荷指标比较[54]Table 2 The contrast of aerodynamic load[54]

表3 列车运行姿态指标比较[54]Table 3 The contrast of vehicle body attitude[54]

崔涛等[55-56]采用离线式流固耦合计算方法研究了高速列车通过站台的安全性，但该方法仅适用于无环境风条件。崔涛[55]采用显式耦合方法分析了高速列车交会时的流场特性和列车运行安全性，发现在考虑流固耦合效应时，交会时的高速列车表面压力波动、气动载荷、列车运行的动力学响应及运行安全性指标均有一定程度增大，列车交会的安全性降低。图16 和17 给出了有/无环境风条件下高速列车350 km/h 等速交会时的表面压力分布。崔涛等[57-59]还采用稳态流固耦合计算方法对侧风环境下高速列车交会安全性开展了研究。在侧风作用下，列车姿态发生变化，但当侧风恒定时，列车姿态最终进入稳定状态。因此，可以采用隐式耦合方法对侧风作用下列车姿态变化的最终状态进行分析，并采用离线仿真方法计算列车的动力学指标。如图18 所示，与不考虑列车姿态变化相比，在考虑列车姿态变化的情况下，头车受到的横向气动力、垂向气动力、侧滚气动力矩和俯仰气动力矩均明显增大。由于气动载荷增大，列车运行脱轨系数和轮重减载率等均明显增大，列车运行的安全性降低，如图19 所示。

图16 无风条件下350 km/h 等速交会[57]Fig.16 Same velocity rendezvous at speed of 350 km/h without wind[57]

图17 10 m/s 侧风条件下350 km/h 等速交会 [57]Fig.17 Same velocity rendezvous at speed of 350 km/h with sidewind at speed of 10 m/s[57]

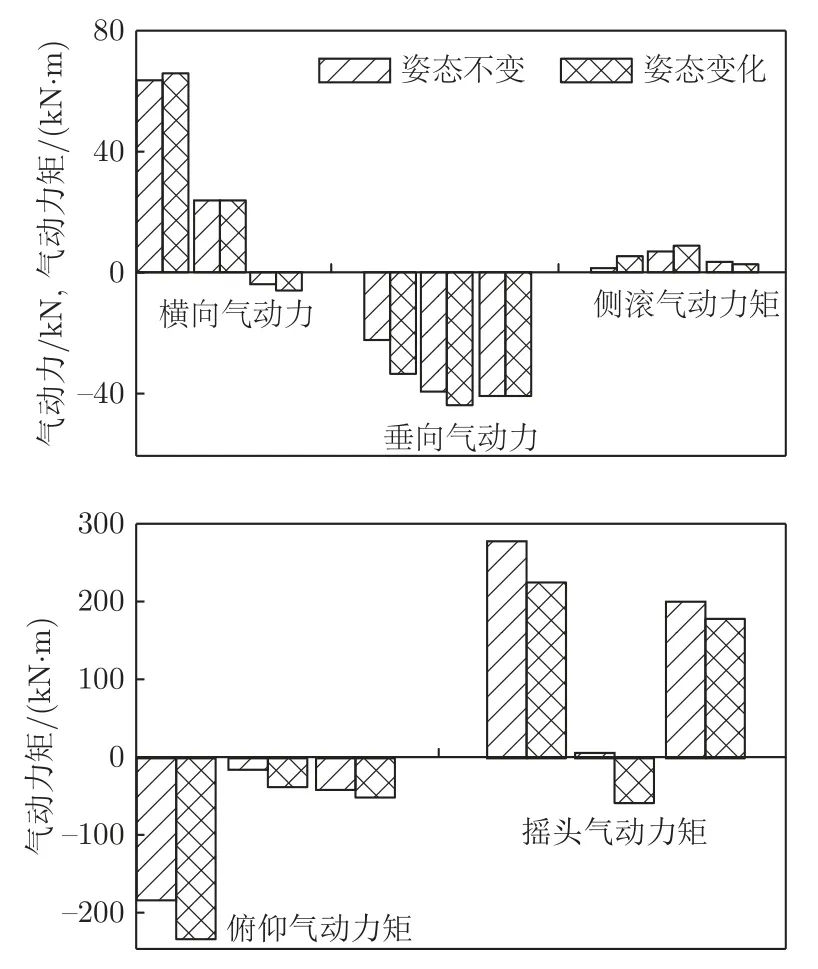
图18 头车、中间车和尾车的气动载荷[57]Fig.18 Aerodynamic load of head,middle and tail vehicle[57]

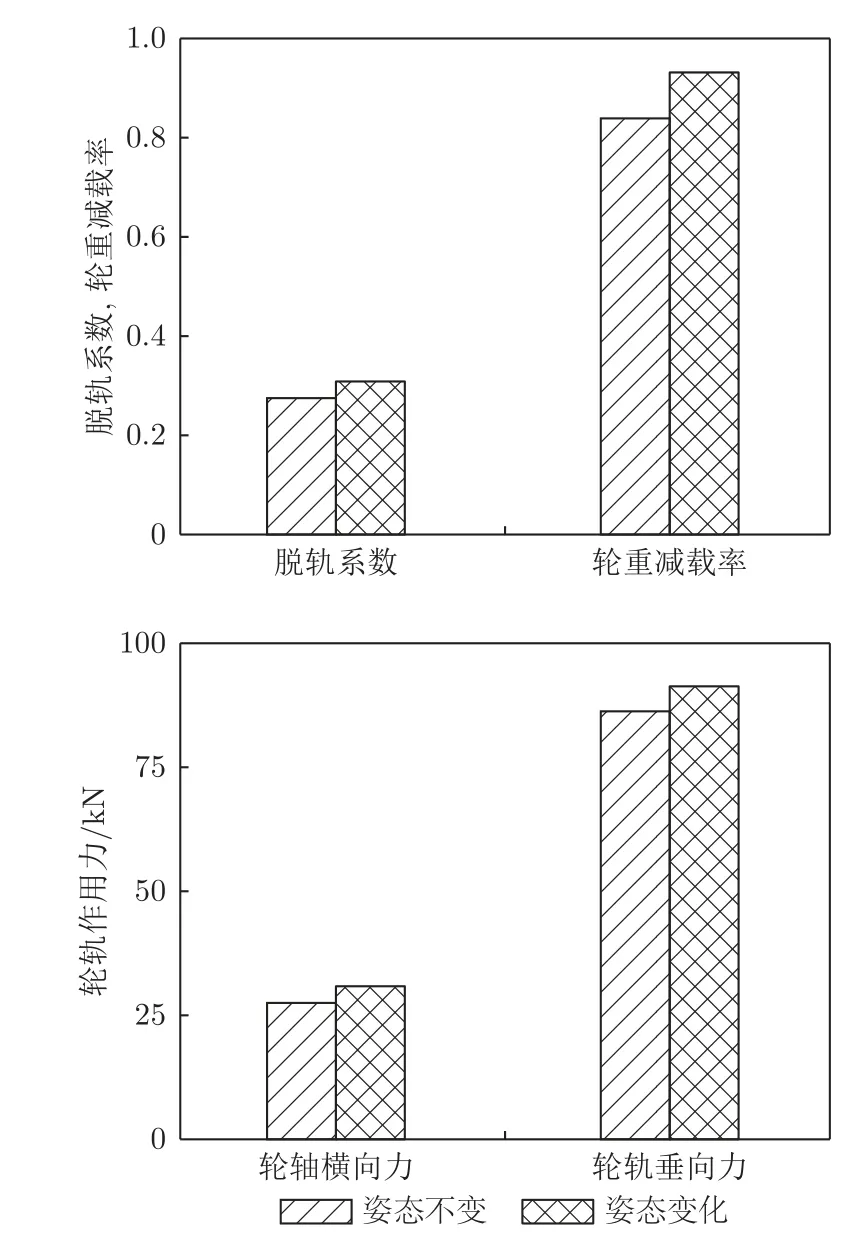
图19 运行安全性指标[57]Fig.19 The operational safety factor[57]

现有的列车流固耦合计算分析结果表明，流固耦合效应会导致列车气动载荷指标和安全性指标增大，列车运行安全性降低，在相关研究中必须考虑流固耦合效应。此外，离线仿真法虽然具有更高的效率，但是由于未实时传输数据，导致计算结果偏离真实情况。因此，在真空管道列车流固耦合研究中，应采用在线的流固耦合计算方法。

3 真空管道列车流固耦合关键技术

3.1 真空管道列车流场分析技术

真空管道列车高速运行过程中，复杂变化的管道压力环境导致车外压力波动及列车压力载荷变化，激励列车系统产生动力学响应，使列车运行姿态产生变化，进而加剧流场变化。与传统高速列车流场分析相比，真空管道列车流场分析具有特殊性。真空管道形成的封闭环境使列车运行环境中的波系更为复杂，悬浮运行的列车姿态变化也需在流场分析中作为重要输入。基于现有真空管道流场研究成果，在后续研究中需重点将真空管道列车姿态这一因素引入流场分析，建立计算精度较高，能够准确反映流场特性，体现复杂波系的产生、反射和传播特性且兼顾计算效率的流场分析模型。针对不同问题，可以采用二维模型或三维模型进行计算，提高研究效率。

3.2 真空管道列车流固耦合联合仿真技术

真空管道列车流固耦合分析需同时进行气动计算和车辆动力学计算。针对高速列车流固耦合问题，李田、崔涛等提出了多种流固耦合计算方法，如离线计算、交互式计算、内嵌式计算及平衡状态法等，主要思路是联合气动计算软件与动力学计算软件（或程序），相互传递气动载荷数据和列车姿态参数作为彼此的输入条件。

真空管道内波系复杂，列车处于时变载荷状态，在激波作用下，列车局部可能形成突变载荷，尤其是在列车加速或减速状态下。因此，在流固耦合计算中需实时传输时变气动载荷数据和列车姿态参数。此外，列车姿态参数对真空管道内波系的产生和传播条件也存在影响，列车姿态变化幅度过大，会产生新的压缩波或膨胀波。因此，针对真空管道列车复杂多变的流场环境及悬浮运行的车辆动力学特点，需基于现有高速列车流固耦合计算方法和技术，提出一套可准确计算真空管道列车流固耦合问题的方法和技术。在列车动力学计算模型中应施加时变气动力、气动力矩及局部气动力，以体现气动载荷的特殊性。

3.3 气动载荷下的真空管道列车控制技术

真空管道列车悬浮运行于真空管道中，在流固耦合效应及管道内各种激波作用下，列车受到时变气动载荷及冲击载荷，其运行姿态发生改变。为避免列车姿态及气动环境发生剧烈变化，导致列车运行安全性降低（甚至与管道发生碰撞），需在列车动力学计算模型中加入列车控制技术，将气动载荷下的列车运行姿态变化控制于合适范围内，确保列车安全运行。

控制技术研究可以从2 个方面开展：一方面，设计合理的真空管道列车气动外形，减小列车的气动力变化；另一方面，可以在列车内部设置悬挂及控制机构，主动调整列车相对悬浮轨道的姿态。

4 结论与展望

真空管道列车利用磁悬浮技术和管道真空运行环境，理论上可实现超过1 000 km/h 的运行速度。但封闭的真空管道导致气动环境复杂，同时列车悬浮运行使列车运行姿态极易发生改变，流固耦合效应明显。本文针对真空管道列车的流固耦合问题，对真空管道列车气动研究进展、轨道列车流固耦合特性研究进展进行了综述，分析了真空管道列车流固耦合关键技术，得到以下结论：

1）真空管道列车管道内气体的阻塞效应对列车气动阻力系数起决定性作用。现有气动载荷特性研究局限于对真空管道列车气动阻力的研究，而列车在实际运行中还受到升力、横向气动力、气动力矩的影响，研究者需对这些气动载荷给予关注。

2）真空管道内存在各类激波，其气动环境比开放流场远为复杂，且各类激波的传播、反射相互叠加使列车运行流场环境具有高度的非稳定性。不稳定的激波簇结构对列车产生时变气动载荷，列车在时变的气动升力、气动力矩及各种冲击性气动载荷作用下，运行特性发生变化。

3）在轨道列车流固耦合研究中提出的联合仿真法、内嵌式联合仿真法及平衡状态法，均可作为真空管道列车流固耦合研究的参考和借鉴，但真空管道列车流固耦合研究还需考虑真空管道列车的特殊性，重点关注时变气动载荷和局部冲击载荷的影响。在动力学计算模型中应施加时变气动力、气动力矩及局部气动力，以体现气动载荷的特殊性。

4）流固耦合效应会导致列车受到的气动载荷指标和列车安全性指标增大，运行安全性降低。离线流固耦合分析方法虽然具有更高的效率，但会导致计算结果偏离真实情况。在真空管道列车流固耦合研究中，需采用在线流固耦合计算方法。

在真空管道列车流固耦合问题研究中，需重点研究开发真空管道列车流场分析技术，关注列车姿态对流场特性的影响；开发真空管道列车流固耦合分析技术，实现高效准确的流固双向耦合计算，准确分析列车气动特性和动力学特性；开发真空管道列车控制技术，实现真空管道列车受控安全运行。

流固耦合问题是真空管道列车技术发展面临的重要问题。在未来研究中，需进一步借鉴传统高速列车和常规磁浮列车的研究方法和手段，并积极寻求创新与突破。