多孔介质对风洞管道内压缩波传播的影响

周廷波，于馨凝，周国龙，贾乐凡，张家忠,*

1.中国空气动力研究与发展中心 设备设计与测试技术研究所，绵阳 621000

2.成都流体动力创新中心，成都 610072 3.西安交通大学 能源与动力工程学院，西安 710048

0 引 言

磁浮飞行风洞是一种利用磁浮系统驱动模型开展试验的新型风洞设备[1]，主要包括风洞结构系统、磁浮驱动系统和试验测控系统。磁浮飞行风洞建筑主体为一等截面长直封闭管道，依次划分为隔离段、加速段、测试段、减速段等。试验时，磁浮驱动机构携带模型在加速段加速至特定速度后进入测试段完成试验。模型在加速段运动过程中产生压缩波，压缩波在风洞管道内传播至风洞端面后反射，并可能在测试段与模型发生碰撞，由此可能造成模型阻力上升，干扰试验结果。因此须采取适当方式减小压缩波强度，削弱甚至消除反射压缩波对测试段模型的影响。

管道内压缩波的削弱/消除在国内外已有广泛研究。例如，中南大学张洁等[2]在高速磁浮列车隧道内引入空腔结构，从而达到降低隧道出口处压缩波强度的目的，类似的方法在日本也有报道[3]。此外，日本新干线还采用突扩结构[4]、侧面开孔[5]等方式削弱隧道内传播途中的压缩波强度。上述空腔及突扩等方法仅适用于开放管道结构，对封闭管道内反射压缩波的削弱能力较差。因此，须寻找一种适用于封闭管道内部，且对正向和反向压缩波强度均有削弱作用的方法。

多孔介质是由骨架及由骨架分隔成的大量均匀分布的微小孔隙所组成的物质。基于其孔隙度与渗透性，多孔介质对通过其中的流体具有压降和吸能特性[6]。例如，海上鱼类养殖网箱及其中的鱼类可视为一种多孔介质，其整体对通过的海流有极强的削弱作用[7]；泡沫铝作为一种新型多孔介质被广泛应用于防爆领域[8]；作为过滤装置使用时，多孔介质对通过其中的流体具有流动阻力[9]。基于上述特性，适当构型的多孔介质对通过其中的压缩波能够起到明显的削弱作用[10]，且具有结构简单、易于维护等优点。本文依据现有的多孔介质压降模型构建描述多孔介质针对压缩波的压降特性描述方程，并利用数值模拟方法探究不同参数的多孔介质对压缩波的削弱作用。

1 多孔介质压降模型

1.1 现有压降模型

流体通过多孔介质产生的压降与多孔介质的几何结构、孔隙度、渗透性及流体物性参数相关。1956 年，Darcy[11]通过试验得到了反映流体通过多孔介质区域前后压强变化与多孔介质物性参数之间关系的Darcy 公式：

式中：v为流体速度，m/s；μ为流体动力黏度系数，kg/(m·s)；K 为Darcy 渗流系数；p 为流体压强，Pa；ρ 为流体密度，kg/m3；g 为重力加速度，m/s2。

根据Darcy 的模型，通过多孔介质的流体压降与流体流速线性相关，但后续研究发现这一结论具有一定的局限性。Forchheimer[12]通过进一步试验研究发现，流体通过多孔介质的压降还与流速的二次项有关，并提出了Forchheimer 方程用以描述多孔介质压降特性：

式中：Δp 为流体压降，Pa；ΔL 为流动方向的多孔介质厚度，m；A、B 为方程参数。

Forchheimer 方程为通过流体压降试验得到的经验方程，A、B 根据试验结果拟合得到。Ergun[13]研究了多孔介质物性参数对其压降特性的影响，并在Forchheimer 方程的基础上引入多孔介质的孔隙度与颗粒直径参数，得到了Ergun 方程：

式中：ε 为多孔介质孔隙度；dp为多孔介质粒径，m；E1、E2为方程参数。

Ergun 方程在一定程度上反映了多孔介质物性参数对其压降特性的影响规律，但该方程仅考虑了空隙尺度基本相同且在空间内均匀分布的多孔介质，方程参数仍须通过试验拟合。

1.2 管道内压缩波压降模型

1956 年，Biot[14]提出了描述弹性波在饱和流体多孔介质中传播规律的波动方程，但其关注点主要在于弹性波穿过多孔介质时的多孔介质骨架应力应变变化。近年来，多孔介质作为吸声材料在降噪领域也得到了广泛研究及应用[15]。目前针对弹性波在多孔介质内传播的研究以声波频域特性为主。与本文所研究的风洞内压缩波相比，声波强度较低，在传播过程中仅包含能量传递；而压缩波强度较高，在传播过程中包含能量及动量传递。对于均匀多孔介质，流体流经其内部产生的动量源项可表示为：

式中：Si为动量源项，N/m3；α 为多孔介质渗透率，m2；vi为沿多孔介质厚度方向的速度分量，m/s；C2为惯性阻力系数，m-1。同时，定义黏性阻力D=α-1，单位为m-2。可以看出，动量源项的方程形式与Forchheimer 方程相同。

对于管道内压缩波的产生及传递过程，国内外学者已有相关研究。根据湖南大学强光林[16]、西南交通大学周鹏[17]等的结论，列车在隧道内加速运动时，列车头部会产生包含弓形激波、菱形激波的压缩波系，这些波系在向前传播足够长距离后，在列车运动前方引起的管道内压力变化呈准一维特征[18-19]。据此可将式（4）改写为：

对于管道内充分发展的压缩波通过多孔介质的情况，由于环境流速几乎为0，在压降过程中惯性阻力系数起主要作用。为了对不同骨架的多孔介质建立统一的压降方程，引入多孔介质通流比S，即每单位体积多孔介质区域的通流面积，单位为m-1。对于Ergun 方程所研究的球形多孔介质，有：

由此得到描述管道内压缩波通过多孔介质区域压降规律的方程：

式中：C 为方程参数。可以看出，式（7）中方程参数C 与惯性阻力系数C2的关系为：

由此可见：对于某确定工况下的多孔介质，其风洞内压缩波消波能力的影响参数主要包括惯性阻力系数C2、多孔介质厚度ΔL 及流动速度v。在本文所研究的环境流速近似为0 的工况下，流动速度与流体压强p 线性相关。后文数值模拟部分将研究这些参数对风洞管道内多孔介质消波能力的影响。

2 数值模拟及分析

2.1 物理模型

2.1.1 基本假设

为简化计算并保证足够的精度，作如下假设：

1） 流场内气体为理想可压缩气体。

2） 多孔介质在空间上均匀分布，且呈各向同性。

3） 多孔介质的物性参数均为常数。

4） 多孔介质为开孔结构。

5） 多孔介质固体骨架与流体处于局部热平衡，且无任何化学反应。

6） 忽略流体流动过程中的黏性耗散。

2.1.2 几何模型与网格划分

参考磁浮飞行风洞的部分设计，建立直径6 m、长100 m 的圆形管道，管道中段40～60 m 处按一定规律布置若干层多孔介质，如图1 所示（图中绿色线条表示多孔介质）。

图1 几何模型Fig.1 Geometric model

对该几何模型进行网格划分，并在壁面及多孔介质区域进行加密。由于压缩波在传递过程中呈准一维特征，因此将该管道模型简化为二维平面，贴近壁面处第一层网格高度为10-5m。本文数值模拟时间步长为0.000 5 s，因此沿压缩波传播方向最小网格尺寸设为0.1 m，多孔介质区域内最小网格尺寸为0.01 m，如图2 所示。对网格数量进行无关性分析：在入口边界施加持续时间0.01 s、速度300 m/s 的速度脉冲；设置惯性阻力系数为5 m-1；多孔介质布置为单层，厚度1 m。分析结果如图3 所示，可以看出：当网格数量小于20 万时，网格较为粗糙；网格数量大于50 万时，计算结果基本相同。为了提高计算精度，后文采用网格数为643 848 的加密方式。

图2 网格划分Fig.2 Grid division

图3 网格无关性分析Fig.3 Grid independence test

2.2 数值模拟工况

管道设置为一端开口一端封闭。开口端设置为速度入口边界，并利用UDF 输入速度脉冲以尽量贴合压缩波在磁浮飞行风洞中传播的实际情况。定义压缩波强度 pc为压缩波经过时当地流体压强 p 的极大值，根据相关文献的数值模拟[16]及试验结果[20]可知：对于定常环境下列车通过隧道引起的压缩波，pc与列车速度正相关。由于充分发展的激波扰动区呈准一维分布特征[18]，且根据列车长度、头部形状及行驶状态不同，压缩波强度大约分布在5～15 kPa[21-22]，本文设置进口脉冲速度为50～300 m/s，探究常压环境下不同压缩波强度对多孔介质消波能力的影响。为了探究其他参数对多孔介质消波能力的影响，对相关参数作如下设置：

方式1：多孔介质布置为单层、厚度1 m，设置惯性阻力系数为5 m-1；在入口边界施加持续时间0.01 s、速度分别为50、100、150、200、250 和300 m/s的速度脉冲，由此探究多孔介质对不同强度压缩波的消波能力。

方式2：在入口边界施加持续时间为0.01 s、速度为300 m/s 的速度脉冲，多孔介质布置为单层、厚度1 m，分别设置惯性阻力系数为1、5、10、15 和20 m-1，由此探究惯性阻力系数对多孔介质消波能力的影响。

方式3：在入口边界施加持续时间为0.01 s、速度为300 m/s 的速度脉冲，设置惯性阻力系数为5 m-1，多孔介质布置为单层，厚度分别为0.1、0.5、1.0、1.5 和2.0 m，由此探究不同厚度对多孔介质消波能力的影响。

方式4：在入口边界施加持续时间为0.01 s、速度为300 m/s 的速度脉冲，设置惯性阻力系数为5 m-1、总厚度为1 m 的多孔介质，层数分别设为1、2、3、4、5 层（各层间隔均5 m），由此探究总厚度相同时层数对多孔介质消波能力的影响。

方式5：在入口边界施加持续时间为0.01 s、速度为300 m/s 的速度脉冲，设置惯性阻力系数为5 m-1，多孔介质布置为单层、厚度1 m，设置环境压力为10.0、5.0 和0.10 atm（1 atm=1.01 × 105Pa），由此探究环境压力对多孔介质消波能力的影响。

2.3 结果分析

2.3.1 压缩波强度对多孔介质消波能力的影响

按上述方式1 设置各参数，多孔介质设于风洞管道内50 m 处，并以无多孔介质情况作为对照。在管道中心40 和60 m 处设置监测点读取管道内压力随时间的变化，其结果如图4 所示。

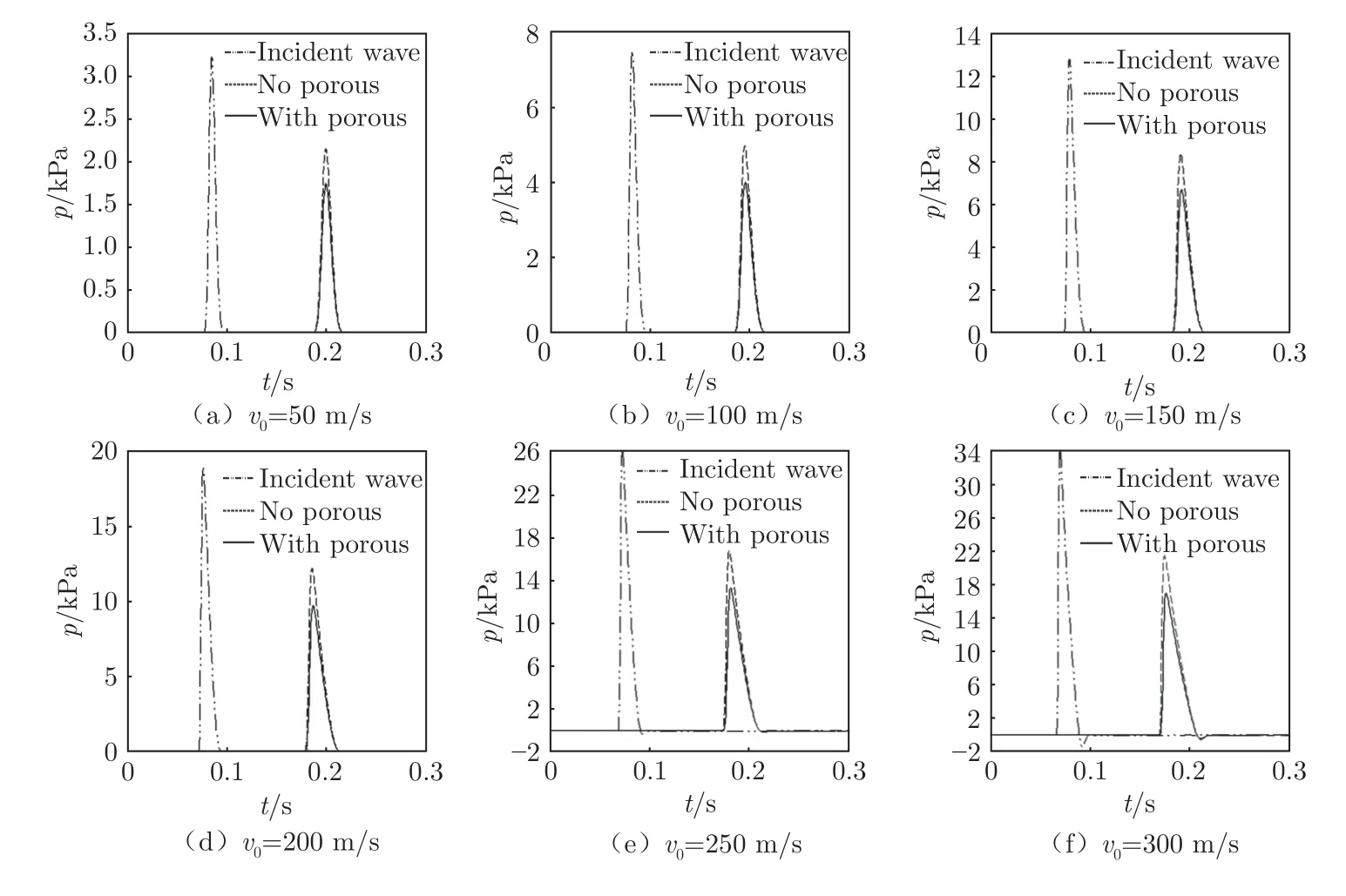
图4 不同压缩波强度下多孔介质消波性能Fig.4 Wave attenuation performance of porous media with different compressional wave strengths

从图4 可以看出：压缩波在管道内以声速传播，当其通过监测点时，监测点处压力先急剧升高，然后降低至略小于环境压力后再迅速恢复至环境压力。当压缩波通过多孔介质时，多孔介质对其有明显的压降作用。

入口脉冲速度v0提高，压缩波强度随之提高，压缩波通过多孔介质的压降Δp 也随之提高。图5 为多孔介质压降Δp 随入口脉冲速度v0的变化图，图6为多孔介质压降Δp 与无多孔介质条件下压缩波强度p0之比随入口脉冲速度的变化图。

图5 不同强度压缩波通过多孔介质的压降Fig.5 Pressure drop of compressional wave passing through porous media with different strengths

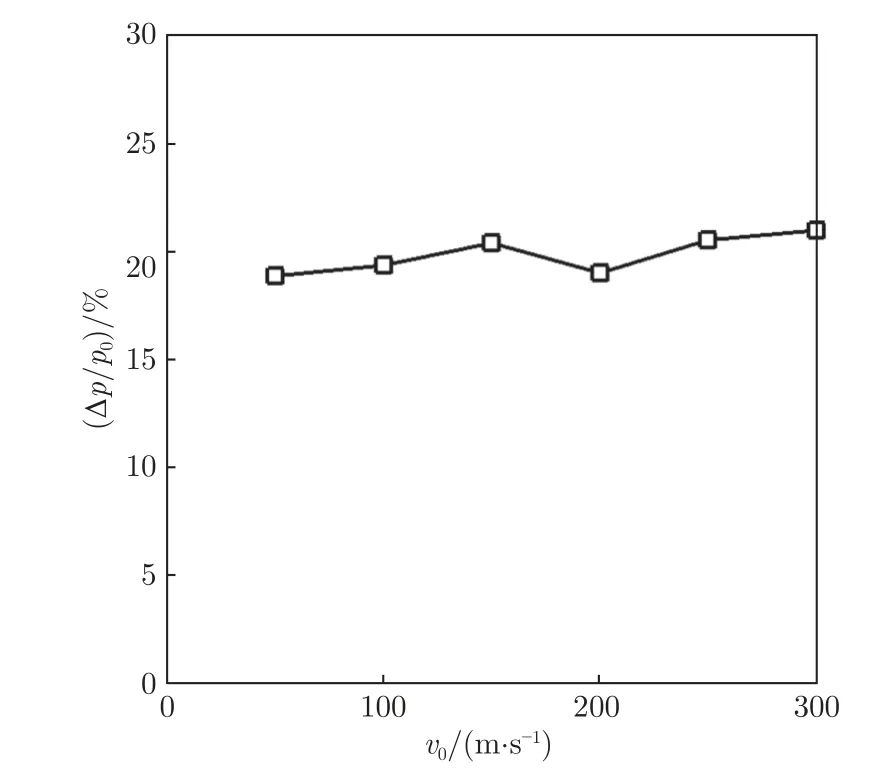
图6 不同强度压缩波通过多孔介质的压降百分比Fig.6 Pressure drop（percentage） of compressional wave passing through porous media with different strengths

结合图5 和6 可以看出：压缩波通过多孔介质的压降随着压缩波强度增大而增大，且其增大的比例基本相同，这说明多孔介质对不同强度的压缩波均能起到相似比例的消波作用，对工况变化的适应性较强。

2.3.2 惯性阻力系数对多孔介质消波能力的影响

在风洞管道内50 m 处按照方式2 设置参数进行数值模拟，并以无多孔介质情况作为对照。在管道中心线40、60 m 处设置监测点读取管道内压力随时间的变化，结果如图7 所示。

图7 不同惯性阻力系数下多孔介质消波性能Fig.7 Wave attenuation performance of porous media with different C2

从图7 可以看出：当压缩波通过多孔介质时，其压降随惯性阻力系数增大而增大；但随着惯性阻力系数增大，部分压缩波未能通过多孔介质区域而是被多孔介质反射，反射波强度同样随惯性阻力系数增大而增大。

2.3.3 厚度对多孔介质消波能力的影响

在风洞管道内50 m 处按照方式3 设置参数进行数值模拟，并以无多孔介质情况作为对照。在管道中心线40、60 m 处设置监测点读取管道内压力随时间的变化，结果如图8 所示。

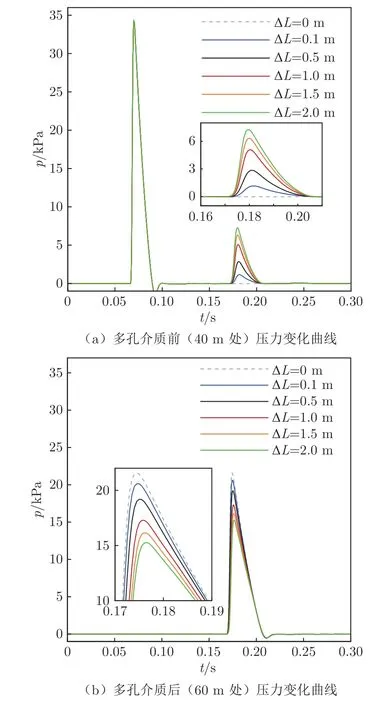
图8 不同厚度多孔介质的消波性能Fig.8 Wave attenuation performance of porous media with different thickness

从图8 可以看出：多孔介质对通过压缩波的压降同样随其沿流动方向的厚度增大而增大，且随着多孔介质厚度增大，同样出现了部分压缩波被多孔介质反射的现象。

综合图7 和8 的结果可知，多孔介质对压缩波的消波能力与其厚度和惯性阻力系数成正比，这一结果符合式（7）的结论。值得注意的是：随着多孔介质厚度/惯性阻力系数增大，被多孔介质反射的压缩波强度也同样增大，这会导致多孔介质在实际应用中无法达到预期的消波效果。因此，须寻找适当的方法在保持多孔介质消波性能不变的情况下减小其反射的压缩波强度，以获得更好的整体消波性能。

2.3.4 层数对多孔介质消波能力的影响

根据图8 所得结果，多孔介质反射的压缩波强度随多孔介质厚度增大而增大。因此，猜测若在保持多孔介质总厚度不变的情况下增加层数，就可以减小其反射压缩波强度。为了验证这一猜测，在风洞管道内40～60 m 范围内按照方式4 中参数布置多层多孔介质，并以无多孔介质情况作为对照。在管道中心线40、60 m 处设置监测点读取管道内压力随时间的变化，结果如图9 所示。

图9 不同层数多孔介质的消波性能Fig.9 Wave attenuation performance of porous media with different layers

从图9 可以看出：在保持多孔介质总厚度不变的情况下，增加多孔介质层数确实可以减小其反射压缩波强度。此外还可注意到，随着层数增加，多孔介质区域后压缩波强度下降；当层数变为2 时其下降效果明显，但层数从2 变化至5 时其压降变化较小；随着层数增加，压降效果甚至略有下降。这是因为当层数由单层增加至2 层时，部分压缩波在2 层多孔介质间发生多次反射并发生能量耗散，从而使多孔介质在整体厚度不变的情况下压降性能提高；但随着多孔介质层数继续增加，单层多孔介质厚度降低，压缩波在各层多孔介质间的反射压缩波强度降低，通过多孔介质的压缩波强度提高，使其结果更加趋近无反射压缩波时的消波情况，因此层数从2 变化至5 时，消波性能变化不大甚至略有下降。

2.3.5 环境压力对多孔介质消波能力的影响

在风洞管道内50 m 处按照方式5 设置单层厚度1 m 的多孔介质，在管道中心线40、60 m 处分别设置监测点读取管道内压力随时间的变化，结果如图10 所示。从图10 可以看出：当环境压力分别为0.1、0.5 和1.0 atm 时，多孔介质前压缩波强度分别为29.51、14.75 和2.94 kPa，多孔介质后压缩波强度分别为18.69、9.30 和1.79 kPa。3 种环境压力下，多孔介质对压缩波的消波比例均保持在40%左右。

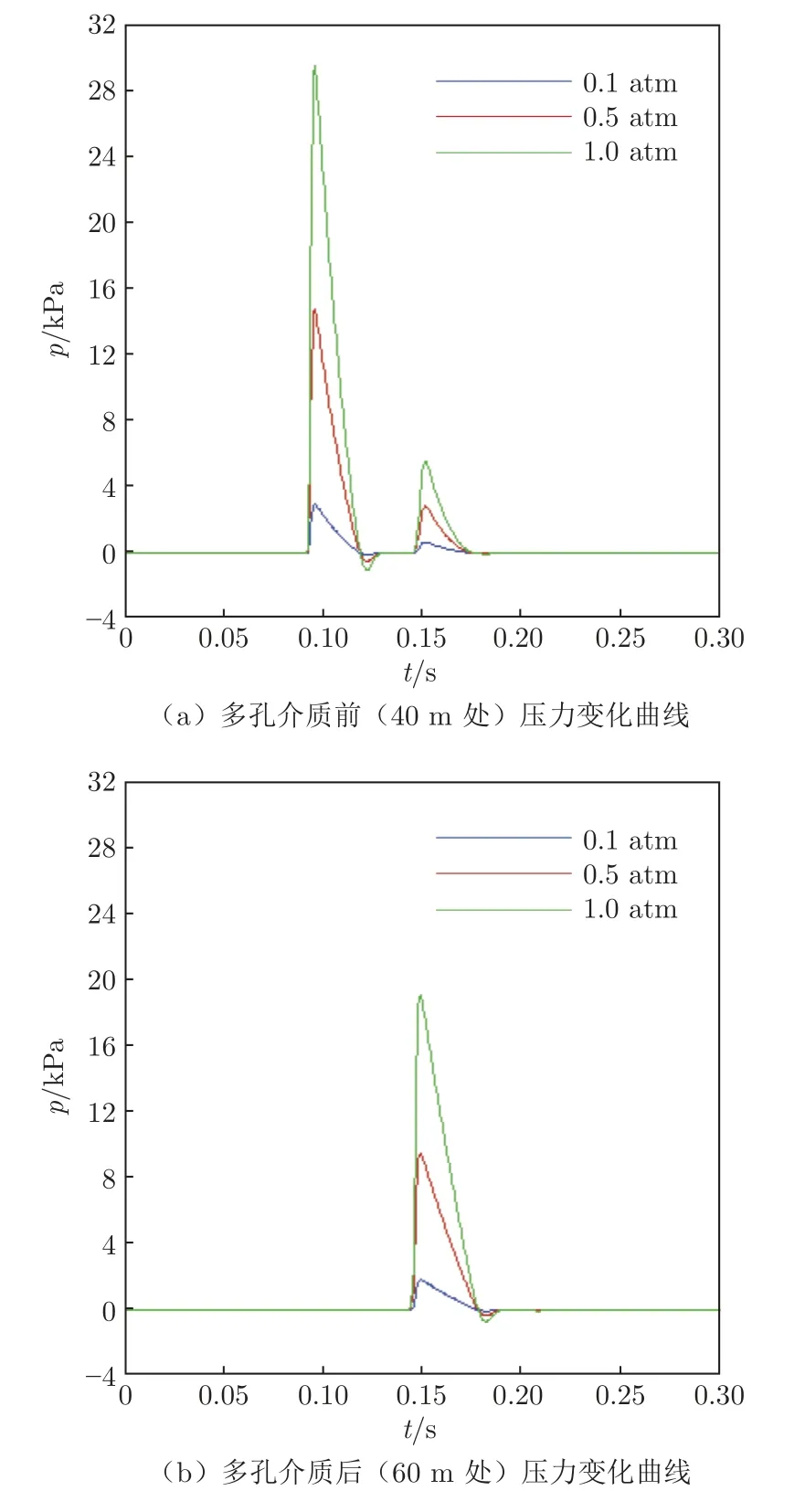
图10 不同环境压力时多孔介质的消波性能Fig.10 Wave attenuation performance of porous media with different ambient pressure

根据相关文献[17]，高3.15 m 的列车在0.000 1 atm下以1 250 km/h（约347 m/s）的速度运行时，车辆前方产生的压缩波强度约为18 Pa。本文所研究管道直径6 m，在0.000 1 atm 的环境压力下空气分子的平均自由程为9.20×10-5～9.20×10-3m[17]，计算得到其Knudsen 数范围为1.53×10-5～1.53×10-3m，小于0.01 m，因此连续介质假设依然成立。本文设置环境压力为0.000 1 atm，进口脉冲速度为347 m/s，其他参数不变，数值模拟结果如图11 所示。图11 中除40、60 m 处的监测点外，增加了5 m 处的监测点以与相关文献数据进行比对。根据5 m 处监测点数据，以347 m/s 输入速度脉冲所产生的压缩波强度约17.2 Pa，与文献[17]中所得结果（18 Pa）较为接近。在0.000 1 atm 环境压力下，多孔介质前压缩波强度约3.40 Pa，多孔介质后压缩波强度约1.42 Pa，消波比例达到59.24%。结合图10 的结果，说明多孔介质可以在较宽的环境压力范围内保持良好的消波能力。

图11 环境压力0.000 1 atm 时多孔介质的消波性能Fig.11 Wave attenuation performance of porous media at 0.000 1 atm

3 结 论

本文在Forchheimer 方程与Ergun 方程的基础上推导了描述管道内压缩波通过多孔介质区域压降规律的方程，根据方程内影响多孔介质消波能力的参数进行数值模拟，所得结论如下：

1）多孔介质对压缩波有明显的压降特性，且在各压缩波强度下均能起到一定比例的消波作用。

2）多孔介质对压缩波的消波能力随压缩波强度、多孔介质惯性阻力系数及厚度增大而增大；多孔介质惯性阻力系数及厚度增大，多孔介质反射的压缩波强度也随之增大。

3）增加多孔介质层数可以在不改变多孔介质其他参数的情况下降低反射压缩波的强度，从而提高多孔介质的总体消波能力。

4）多孔介质可以在较宽的环境压力范围内（0.000 1～1 atm）保持良好的消波能力。