轨道结构对真空管道磁浮列车气动特性的影响

王潇飞，胡啸，李宗澎，刘剑儒，邓自刚,*，张卫华

1.西南交通大学 力学与航空航天学院，成都 610031 2.西南交通大学 牵引动力国家重点实验室，成都 610031

3.西南交通大学 超高速真空管道磁浮交通研究中心，成都 610031

0 引 言

受制于地表稠密的大气，地面交通工具向更高速度迈进存在巨大挑战。采用低真空管道与高速磁浮相结合的方式，能够消除轮轨接触摩擦，降低空气阻力，实现超高速运输[1]，相关研究已成为近年热点。目前，美国Hyperloop One、HTT、SpaceX，加拿大Trans POD，西班牙Zeleros，荷兰Hardt Hyperloop，韩国铁道研究院，以及国内的中国航天科工集团有限公司、中国空气动力研究与发展中心和西南交通大学都在开展真空管道系统研究[2]。

诸多学者针对真空管道磁浮系统涉及的空气动力学问题（气动热[3]、壅塞流[4-5]、激波等波系结构[6]）开展了数值研究，也有学者研究了各项系统参数（阻塞比[7]、真空度[8]、运行速度[9]、初始环境温度[10]）、加速和减速效应[11]及不同管道和列车几何模型对管道内流动的影响[12-14]。然而，受限于真空管道磁浮系统研究对大功率推进电机和真空管道环境的需求，目前仍缺乏相关试验研究数据。

为开展真空管道内的超高速试验，西南交通大学于2020 年开始建设“多态耦合轨道交通动模型试验平台”（最高试验速度1 500 km/h 的超高速真空管道磁浮交通试验系统）。此前，在建成于2019 年的真空管道高温超导高速磁浮动模型试验平台上已经开展了部分先导性动力学试验[15]。该平台主要由真空管道和永磁轨道-电机作业平台组成，试验速度达到93 m/s。在测试中发现，模型车的垂向振动加速度较大，且向上限位经常与轨道发生碰撞和摩擦，其原因可能在于不平顺永磁轨道产生的随机振动与气动升力的叠加效应。该试验平台的轨道与动模型底部流动间隙过大，是影响模型车气动升力变化、导致垂向振动加速度增大的因素之一。

两条轨道与动模型底部形成了一条矩形槽道（高约100 mm），矩形槽道内的流动受到壁面限制，对列车气动载荷影响较大。与动模型特征尺寸（列车高度H）相比，列车底部流动间隙尺寸过大，其流场与实际状态相差很大，相关研究较为缺乏[16]。此外，该试验平台必须采用推力密度更高、体积更大的双边型直线电机来达到所需加速度，这进一步增大了列车底部的流动间隙。同时，永磁轨道具有特殊的台阶结构，也会导致更多的流动分离，影响管道内的流场发展。以上因素，都会影响管道内动模型试验的流场和气动力测试。

针对以上问题，本文以真空管道高温超导高速磁浮动模型试验平台为研究对象，基于管道内电机平台和永磁轨道的实际布置形式，探究模型车底部矩形槽道对列车气动载荷和管道内流场的影响。

1 数值方法

1.1 几何模型

本文几何模型参考真空管道高温超导高速磁浮动模型试验平台，主要包括真空管道、永磁轨道-电机作业平台及1∶10 模型车，如图1 所示。模型车底部区域的杜瓦（低温保持装置，使超导体维持于超导态）、电机定子、多种传感器及安全保护装置等多种设备会严重干扰列车底部流场计算，而本文研究重点为列车底部间隙变化对模型车气动特性的影响，故在本文数值计算中以包覆形式尽量平滑列车底部，并适当简化永磁轨道-电机作业平台。

图1 真空管道高温超导高速磁浮动模型试验平台Fig.1 The moving model test platform of high temperature superconducting high-speed maglev in evacuated tube

如图2 所示，以模型车高度H=0.38 m 为特征尺寸；总长21.18H，头尾部流线型长度为2.82H；最大车体宽度0.89H，最大横截面积Str=0.118 m2。根据真空管道截面的不同，设置2 个工况：工况A 无矩形槽道（与大多数学者的研究模型相同[17-18]），截面积SA=0.513 7 m2，车-管截面阻塞比βA=0.230；工况B 为动模型试验轨道形式（有矩形槽道），SB=0.523 7 m2，βB=0.226。不同工况下的截面积和截面阻塞比相差较小。悬浮间隙（车底和轨道上表面之间距离）h=0.02 m，轨道高度d=0.1 m。

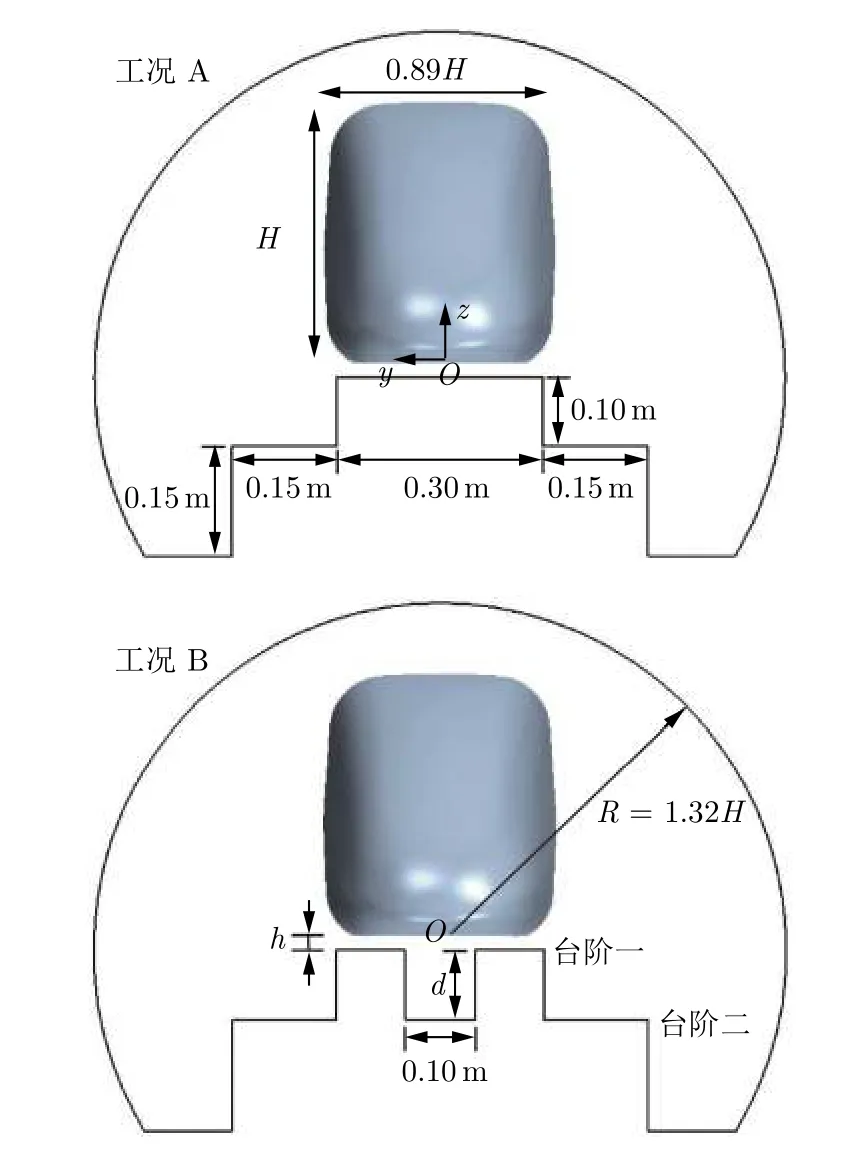
图2 2 种管道截面和列车几何模型Fig.2 Geometric models of two kinds of tubes and train

1.2 计算域与边界条件

如图3 所示，管道长度为263.16H，车头距入口边界84.21H，距出口边界178.95H。不考虑管道两端壁面反射，管道入口和出口边界条件设为无反射黎曼边界（自由流边界），马赫数设为1.0。列车表面设为固定无滑移壁面，真空管道、轨道和平台设为移动壁面，移动速度与风洞气流速度相同。此外，列车壁面与管道壁面的热边界条件都设为绝热。初始时刻管道内的温度T0和环境压力p0分别为288 K 和1 013.25 Pa。

图3 计算域与边界条件Fig.3 The computational domain and boundary conditions

1.3 网格划分

采用非结构化的混合网格对计算域进行网格划分，如图4 所示。对于主体区域，利用STAR-CCM+中的切割体网格生成器划分网格，并对流动复杂区域（如尾流区和列车底部、轨道附近）进行多级网格加密[19]，加密区网格最小尺寸为Lmin、2Lmin、4Lmin。为了捕捉近壁面流动，将列车表面划分为20 层棱柱层网格，拉伸比为1.2，近壁面边界层网格厚度为2.05 × 10-4H，边界层总厚度为3.83 × 10-2H。划分3 组策略相同但密度不同的网格进行网格独立性验证，3 组网格的关键参数如表1 所示。为进一步研究边界层网格的独立性，细网格比粗网格和中网格包含更多棱柱层。

表1 网格分辨率的比较Table 1 Comparison of the grid resolutions

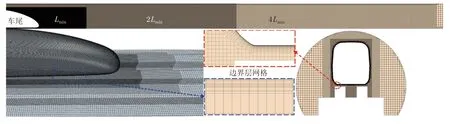
图4 计算网格加密示意图Fig.4 Refinement scheme of the calculation grid

1.4 求解模型与数据处理

本文研究对象为在密封真空管道（1 013.25 Pa）内以340 m/s 速度行驶的磁浮列车，对应马赫数为1.0，需考虑空气的可压缩性[20]。采用三维可压缩、基于剪切应力输运模型SST k-ω 的RANS 方法求解真空管道内磁浮列车周围流场。RANS 方法具有计算速度快等优点，已成为列车空气动力学领域常用计算方法[21-22]，同样适用于本文所研究的问题。SST k-ω 湍流模型可以解决自由来流边界条件中的敏感性问题，且具有很好的预测边界层内的低雷诺数流动和边界层外的完全湍流流动的能力，在高速列车仿真中得到广泛应用[23-25]。在STAR-CCM+中采用有限体积法。耦合求解在可压缩流中鲁棒性更好，能得到更准确的解，尤其是在存在激波的情况下，因此本文采用耦合隐式求解。采用二阶迎风离散格式对流动控制方程中的对流项和扩散项进行离散。采用更适于求解高超声速流动、捕捉激波能力更强的AUSM+无黏流量格式。由于管道内存在激波和膨胀波，空气温度发生巨大变化，因此管道内空气动力黏度服从Sutherland 定律。

为便于比较计算结果，对数据作无量纲化处理，压力系数Cp、阻力系数CD、升力系数CL定义如下：

式中：p、p0、v、D 和L 分别为表面静压、参考压力（初始环境压力）、气流速度、气动阻力和气动升力。1 013.25 Pa 气压下，空气密度ρ=0.012 25 kg/m3。

2 网格独立性与数值验证

2.1 网格独立性验证

表2 比较了基于3 组网格计算的气动阻力系数和气动升力系数。采用中网格与细网格的预测结果相近，阻力系数误差百分比约为0.255%，升力系数误差百分比约为0.318%。

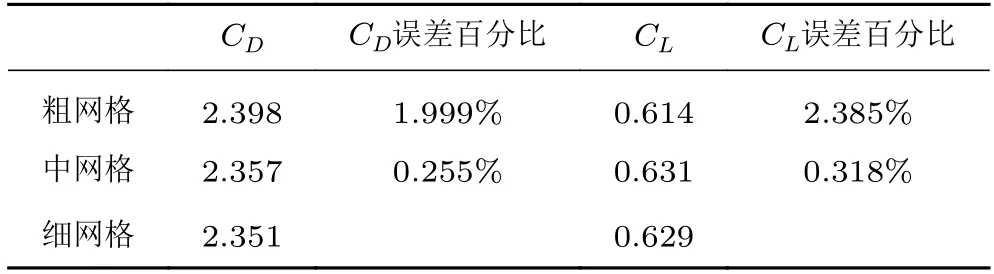
表2 3 组网格计算结果对比Table 2 Comparison of results of three kinds of grids

图5 比较了基于3 组网格计算的z=-0.01 m截面中心线上的列车尾流区压力系数。可以看到，基于中网格和细网格计算的压力系数分布相似，而粗网格尽管可以捕捉到压力系数波动趋势，但与中网格和细网格的波动幅值差异较大。网格独立性研究表明，中网格具有足够的分辨率。因此，本文采用中网格计算真空管道内的流场。

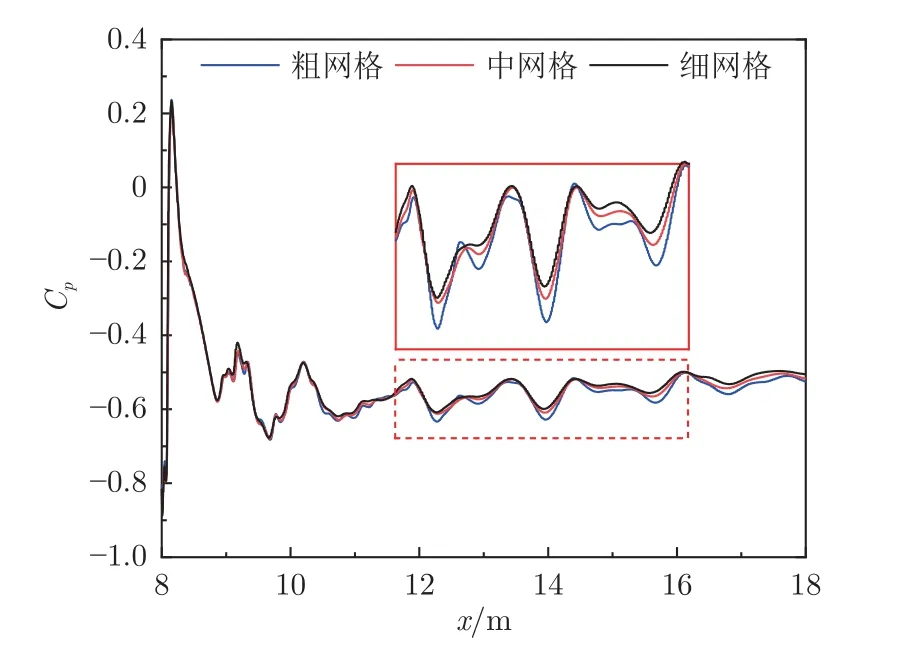
图5 基于3 组网格计算的列车尾流压力系数比较Fig.5 Comparison of the pressure distribution in the wake region

2.2 数值方法验证

目前尚未开展低真空管道列车气动试验，暂无相关试验数据进行对比。为验证本文所采用的数值方法，对经典CFD 外部流动验证案例ONERA-M6三维翼型进行数值计算，并将计算结果与风洞试验数据进行对比[26]。该翼型相关几何参数及风洞试验流场条件详见文献[27]，数值计算初始条件与试验中相同，求解翼型流场的数值方法与本文数值方法相同。气流速度v ＝ 285.65 m/s，弦长c=0.64 m。

图6 为数值计算得到的翼型表面压力系数Cp与试验数据的对比。可以看出，数值计算结果与试验结果总体趋势吻合度较高，本文采用的数值方法能较准确地完成对ONERA-M6 翼型表面压力系数Cp的计算，并准确捕捉到激波现象（图6（a））。因此，本文所采用的数值方法是合理的。

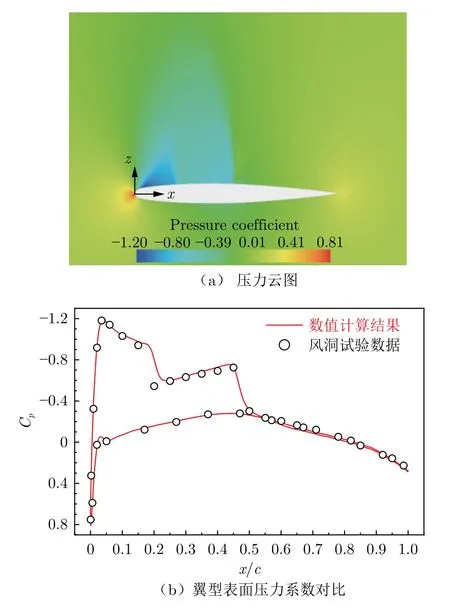
图6 ONERA-M6 翼型表面压力系数Fig.6 Pressure coefficient distribution of ONERA-M6

3 结果和讨论

3.1 管道内流场基本特征

采用工况A（无槽道工况）下的0.2 s 瞬态流场计算结果描述管道内的流场分布和一般规律。图7（a）和（b）分别为管道内流场压力系数分布云图的俯视图和侧视图（图中左端大箭头表示气流运动方向）。在列车前方和后方都产生了一道正激波间断面，将整个真空管道内的流场划分为未扰动区域和活塞区域。在活塞区域，列车与管道壁面形成了一种上下非对称的收敛-扩张进气道（C-D 喷管）模式[28]。由压力系数分布云图可以看到：列车前方为正压高压区，压力最大点出现于列车头部速度驻点；气流从列车前方流经头部上下表面和管道壁面之间形成的收敛段时，气流加速，压力迅速降低；之后高速气流从列车尾部上下表面与管道壁面之间形成的扩张段流出，气流继续膨胀加速至超声速；由于气流过度膨胀，扩张喷管出口（即尾部鼻尖附近）的压力小于管道内初始环境压力，在管道内空间形成斜激波S1（图7（c）），且在尾流区发生较多交替变化的反射激波（在空间上表现为三维激波面）；在激波与剪切层分离、尾涡脱落等作用下，尾流区表现为负压低压区，压力最小点出现于列车尾部附近（S1 激波前）。

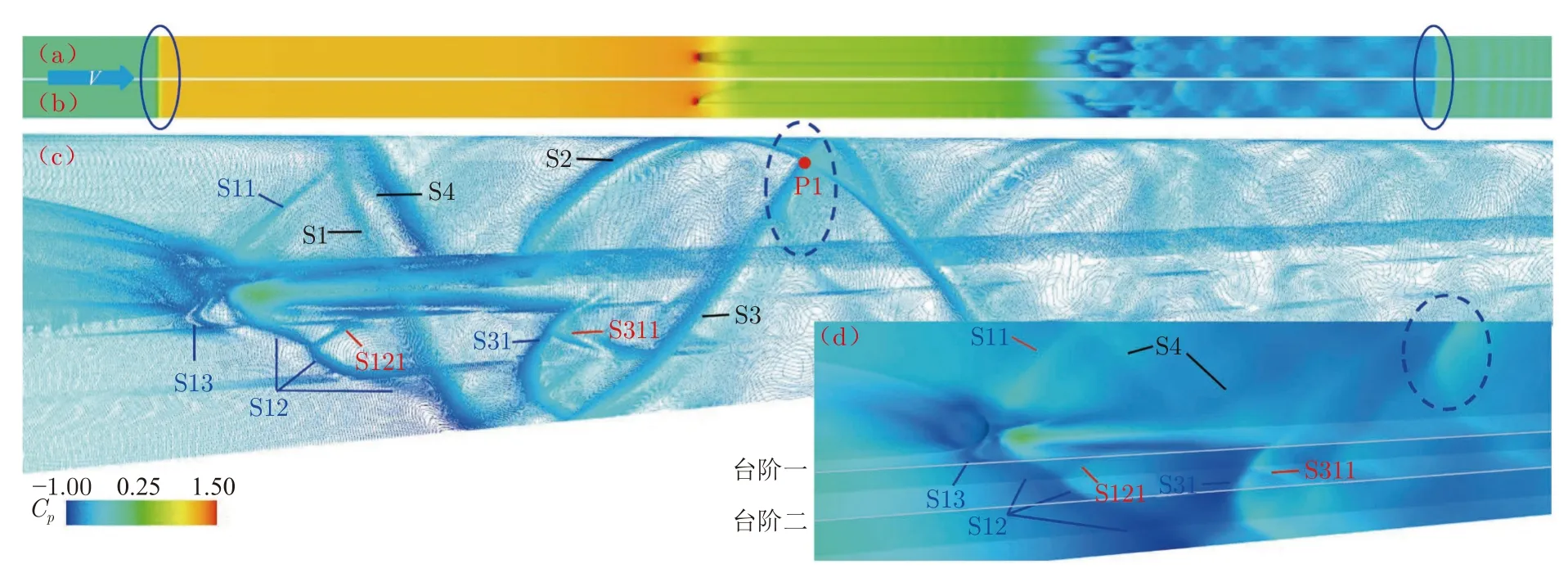
图7 管道内流场空间分布和压力云图Fig.7 The spatial distribution of flow field and pressure in the tube

图7（c）和（d）展示的是列车尾流区压力和激波分布情况。将激波S1 映射至二维截面上，在列车尾部的顶面、侧面和底面形成的激波分别定义为S11、S12 和S13。激波S1 在尾流区传播，被管道内壁两侧面和顶面反射，形成反射激波S2、S3 和S4。反射激波S2 和S3 在传播过程中相交于管道内壁顶面P1 点，焦点附近的流场发生明显转向。

对于尾流区激波的分布，本文研究结果与已有研究结果[29]有2 点不同：其一，本文考虑了电机平台，在平台每一级台阶突变处，激波均会发生反射，产生反射激波S121 和S311 等，使尾部激波分布存在连续反射和跳跃现象，影响尾流发展（台阶处有细小的涡流脱落），导致列车后方尾流区产生更多的压力突变。其二，在工况B（有矩形槽道）下，尾部鼻尖附近存在一道向下发展充分的强斜激波，这也是工况A 和B 的主要区别之一，后文将作详细分析。此外，本文主要关注流动间隙增大对列车底部附近流场和整车气动载荷的影响，瞬态结果与稳态计算结果差别较小，故后文采用时均结果进行分析[30-31]。

3.2 不同流动间隙流场对比

对有/无槽道工况下的管道内压力、速度和流场分布进行对比分析，着重关注列车底部、尾流和台阶突变处的差异。

图8 为2 种流动间隙下列车附近的压力云图。从压力云图可以明显观察到，在2 种工况下，列车前方和列车附近的压力相差较小，而列车后方压力相差较大，尤其是在列车尾部鼻尖附近，流动间隙增大使得底部空间变大，导致该处出现了更为明显的激波，且在S1 引起的反向压力梯度作用下发生了流动分离，形成剪切层[32]，造成激波前的低压区增大。

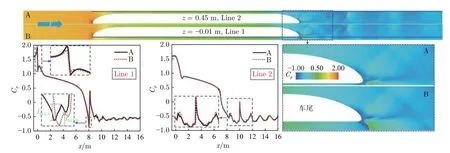
图8 列车附近压力系数分布Fig.8 Pressure coefficient distribution around the train

为量化分析列车附近压力分布，提取列车上方Line 2（管道顶面附近，z=0.45 m）和列车底部附近Line 1（z=-0.01 m）上的压力系数曲线（图8）。在2 种工况下，列车头部和上下表面附近的压力系数相近（工况B 的压力系数值略低于工况A），而尾部和尾流区的压力系数差异明显。对于Line 1，气流进入列车头部下方收敛段向后流动，头车截面逐渐增大，车管间隙逐渐减小，导致压力系数明显下降，马赫数增大；当流动间隙增大时，底部空间增大，阻滞作用减弱，该处压力突变比无槽道时减小。在列车尾部，由于存在激波S13，2 种工况下的压力在激波前后都发生了突变。以激波后压力与激波前压力的差值定义激波强度，则无槽道时激波强度IS13-A=0.13，有槽道时激波强度IS13-B=0.10，后者比前者减弱了23%，且能更明显地识别激波S13（无槽道时，受地面限制，激波现象不明显，易被忽略）。有槽道时，激波在尾流区传播的同时发生更多反射，尾流区压力分布明显区别于无槽道时，且负压系数绝对值更小。对比尾部Line 1 和Line 2 上的压力系数变化，可以看出前者变化更为剧烈，这是由尾部下表面曲率变化比上表面更大、气流膨胀更加剧烈所导致的。

速度是导致压力变化的主要因素。为进一步探究列车底部压力变化的影响因素，提取了Line 1 上的速度变化曲线。如图9（a）所示，可以发现2 种工况下的列车底部速度变化差异明显。来流被列车头部滞止，转向头部上下表面并在收敛段急剧加速，继而进入列车顶部和底部平直段。无槽道时，列车底部空间狭窄，气流在列车底面黏滞作用下逐渐减速，其后在列车尾部扩张段急剧加速至超声速。有槽道时，列车底部空间增大，黏滞作用减弱，气流速度几乎不降低，因此列车底部压力略小于无槽道时。在扩张段，有槽道时的气流速度比无槽道时更大，经过激波面后，气流速度下降程度比无槽道时更小，证实了有槽道时激波强度降低，激波后的速度大于无槽道时，而压力则比无槽道时更小。由图9（b）的速度矢量分布可以看出，在逆压梯度作用下，列车尾部鼻尖处产生了一对反向旋转的旋涡并逐渐分离形成剪切层。经过尾部流动分离后，气流速度明显升高，而后在尾流区激波作用下不断减速继而加速，导致压力波动（波动曲线整体呈减速趋势）。在尾流区，有槽道时的气流速度大于无槽道时，使得尾流区的压力更低。

图9 2 种工况下Line 1 和尾部对称面上的速度分布对比Fig.9 Comparison of velocity distributions on Line 1 and y=0 cross section between two conditions

图10 为列车中部横截面（x=4 m）的流线。可以看出：无槽道时，列车底部气流在阻滞作用下速度降低；有槽道时，部分流经列车底部的气流方向向上，增大了气动升力，对列车产生抬升作用，导致悬浮间隙波动和悬浮不稳定[33]。

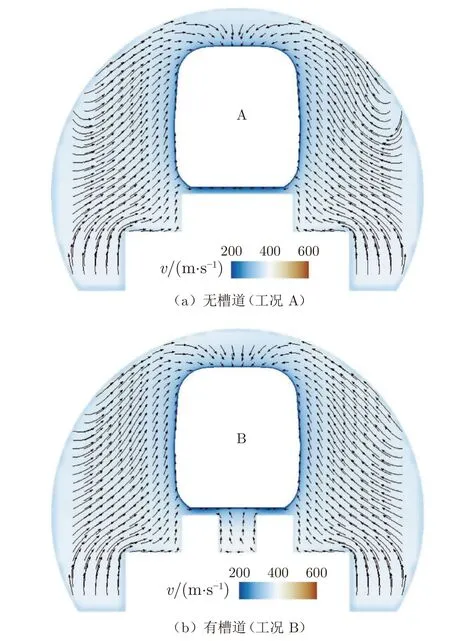
图10 列车中部横截面流线分布Fig.10 Streamlines distribution of cross section in middle train

2 种工况下的尾流区压力存在明显波动和差异，需进一步探明有/无槽道情况下尾流结构的差异。图11 基于等值面Q=1 × 104可视化尾涡结构，并以涡度ωx着色等值面，度量涡流运动能力。从图中可以观察到尾部流线型位置脱落了2 对明显的反向旋转的涡V1 和V2、V3 和V4，2 对涡沿流向和展向运动、上升。该现象与其他文献中列车尾部出现1 对反向旋涡有所不同[34]，这是由于列车尾部分离流在台阶突变附近形成了反向旋转的涡对V3 和V4，并紧贴上方涡对V1 和V2 向后发展，且涡量低于上方涡对（同侧涡V1 与V3 反向、V2 与V4 反向）。为更清晰地识别涡对向后发展的规律，截取了尾流区4 个截面Xi（下标i 为截面位置x 坐标值，如X10即x=10 m 处的截面）。可以发现：2 个涡对在向后发展时逐渐远离轨道中心线；截面X12处的下方涡对基本消失，上方涡对发展距离更远；台阶突变处存在许多不断交替分离的细小涡（图中绿色圆圈标记了部分分离的细小涡），进一步加剧了尾流区的压力波动。

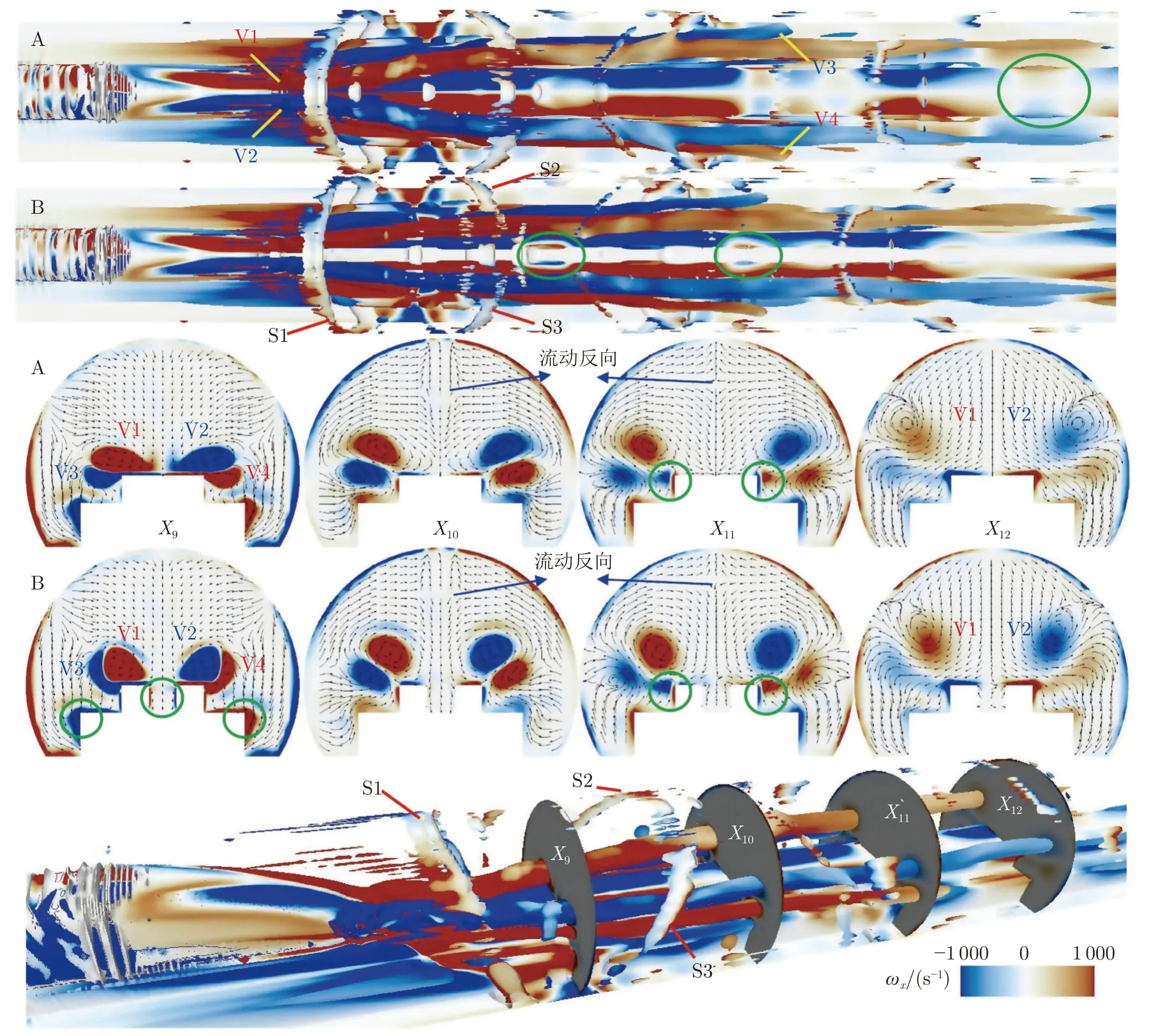
图11 尾涡结构对比Fig.11 Comparison of vortex structures in the wake region

对比2 种工况可以发现：有槽道时，流动空间增大，尾涡更为细长，与无槽道时相比，同一横截面在展向上距离轨道中心线更近，在高度上更靠近轨道；作用于管道两侧内壁面上的涡流影响范围更小，向下游传播距离更远，且在槽道台阶突变处存在更多的流动分离。此外，可以从截面X10和X11上看到，激波作用附近的流动发生了明显转向，导致压力突变。正是在激波与涡对的相互作用下，尾流的复杂程度增加，已有学者就此进行了详细分析[32]。

3.3 气动力变化

在动模型试验时，气动阻力影响电机推进功率设置，气动升力影响列车悬浮系统稳定性。表3 对有/无槽道工况下的列车阻力系数和升力系数进行了对比。有槽道时比无槽道时的阻力系数减小了8.855%，而列车头尾压差阻力约占总阻力的90%，因此总阻力降低主要由压差阻力降低所导致，由图8列车上下表面附近的压力系数曲线（有槽道时的头部和尾部压力系数绝对值均小于无槽道时）可以得出上述结论。另外，阻力降低的原因也可基于阻塞比分析得出：有槽道时，列车底部流动间隙增大，阻塞比降低，导致阻塞效应降低、气动阻力降低。有槽道时比无槽道时的气动升力系数增大了14.312%，主要原因由图10（b）列车底部流线分布可以分析得出：气流流动方向向上，增大了气动升力系数，对列车起到了抬升的作用。

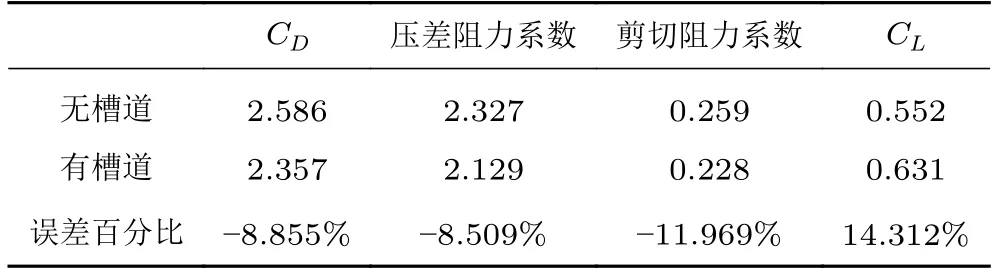
表3 2 种工况下的气动力系数Table 3 Aerodynamic coefficient in two cases

4 结 论

1）真空管道内流场可分为活塞区和未扰动区，永磁轨道和电机平台的存在导致了更多更复杂的激波反射和传播现象产生。

2）永磁轨道和电机平台的台阶形式使尾流区产生更多流动分离和激波反射，导致尾部压力波动。有槽道时，列车上下表面附近压力波动减小，列车尾部激波强度下降，激波现象更明显，尾流更细长。

3）有槽道时，阻力系数减小8.855%，主要原因是列车头尾压差阻力降低；升力系数增大14.312%，主要是由于流动间隙增大，底部气流向上流动产生升力。

本文研究结果可在多态耦合轨道交通动模型试验平台永磁轨道和电机平台前期设计阶段提供气动布局参考。

致谢：感谢国家超级计算郑州中心提供计算资源支持。