谐振腔结构减缓高速磁浮列车隧道出口微气压波研究

宋军浩，姚拴宝，陈大伟，丁叁叁，杨明智

1.中车青岛四方机车车辆股份有限公司，青岛 266111 2.中南大学 交通运输工程学院，长沙 410075

3.中南大学 轨道交通安全教育部重点实验室，长沙 410075

0 引 言

高速磁浮列车利用电磁力克服重力，使列车悬浮在导轨上，采用直线电机无接触导向驱动控制技术，突破传统轮轨列车黏着系数和振动噪声的限制，运行速度可达 600 km/h 以上。更高的运行速度带来了更严峻的空气动力学问题，当高速列车由明线进入隧道，前方空气在隧道内壁面和列车车体形成的环状空间内被压缩，产生压力波作用在车体上，严重影响列车安全和乘客舒适度。压缩波在隧道出口辐射产生的微气压波可能会对周围的建筑玻璃及居民产生不利影响，严重时还会产生爆破噪声[1-2]。

目前对列车-隧道耦合空气动力学的研究主要集中在高速轮轨列车方面。国内外研究表明，隧道出口微气压波幅值与列车进入隧道时产生的初始压缩波及其传播过程中由物理能量耗散和非线性效应引起的出口压力梯度有关。降低微气压波的基本思路主要在列车和隧道两方面：一是优化列车车体断面面积或头型流线[3-6]；二是优化隧道入口形状和在隧道内设置竖井等缓冲结构。Saito 等[7]基于声学理论研究了两级阶梯缓冲入口截面面积比和开孔率对压力梯度的影响。陶伟明[8]对隧道入口喇叭口、直线斜切截面、等截面、扩大截面等目前已有的微气压波减缓措施进行了深入分析，得到多种微气压波减缓措施联合作用下的减缓效果。王田天等[9]采用数值模拟和动模型试验研究了隧道出口断面扩大斜切式缓冲结构的尺寸、开孔数等参数对隧道出口微气压波的减缓特性，最优减缓率达70.9%。史宪明等[10]利用数值模拟对高速铁路隧道外流场进行了分析，基于隧道入口、隧道中部及隧道出口监测点压力梯度值的变化，得到隧道出口微气压波与套衬尺寸特征参数的比例关系。张童童等[11]提出了一种内置式阶梯型缓冲结构，通过数值模拟发现：当缓冲结构布置在距离隧道入口上游60 m 处、扩张形式为三向扩张、长度30 m、截面积150 m2时，对压力梯度的减缓效果为24.7%。闫亚光等[12]基于气动声学理论，对隧道入口的喇叭口型缓冲结构进行优化设计，发现压力梯度随缓冲结构长度增大而减小，该结构可降低压力梯度峰值63.9%。李文辉等[13]对变截面隧道和典型缓冲结构对气动效应的减缓效果进行数值模拟，对比分析了2 种结构对隧道压力波和微气压波的减缓效果。

目前，我国常温常导高速磁浮列车设计速度高达600 km/h，首套高速磁浮系统已在青岛成功下线。高速条件下引发的列车隧道气动效应更加严峻。梅元贵等[14]采用三维数值模拟方法研究了隧道入口有/无设置开口型缓冲结构时的微气压波特征，得到开口型缓冲结构和竖井结构减缓微气压波的临界隧道长度分别为33 和34 km。张洁等[15]研究了隧道出口缓冲结构对600 km/h 高速磁浮列车通过隧道的初始压缩波梯度和微气压波幅值的减缓作用，分析了缓冲结构长度对微气压波幅值的影响。

目前对速度600 km/h 的高速磁浮列车空气动力学问题研究较少。本文在已有研究基础上，针对高速磁浮列车通过隧道时的出口微气压波问题，提出一种在隧道冗余空间使用谐振腔阵列结构的缓冲装置，采用三维、非定常、可压缩N-S 方程和SST k-ω 湍流模型，结合重叠网格技术对高速磁浮列车通过带有不同谐振腔结构隧道的出口微气压波进行数值模拟，分析谐振腔结构对隧道出口微气压波的减缓效果，并采用动模型试验方法进行验证。

1 数值模拟方法

1.1 计算模型

如图1 所示，高速磁浮列车模型采用实车3 编组列车真实外形，由头车 + 中间车 + 尾车组成，全长81.2 m，高4.2 m，宽3.7 m。车体表面平顺化，无凸出附属结构，风挡简化为全包风挡。

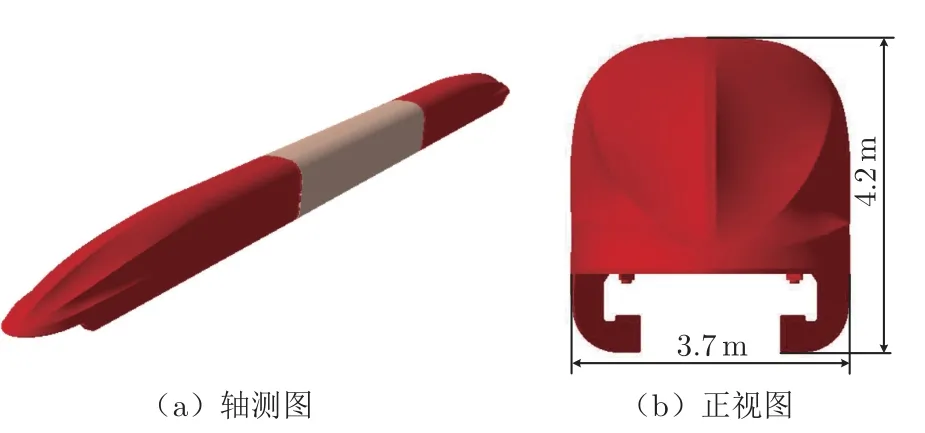
图1 高速磁浮列车计算模型Fig.1 High-speed maglev train model

隧道模型采用T 形轨道梁的单线隧道。隧道长度400 m、净空截面积80 m2，隧道内距离隧道入口20 m 处开始沿隧道长度方向布置谐振腔结构，如图2（a）、（b）所示。当声波传至隧道与谐振腔构成的空间时，在谐振腔的声阻耗损作用下消耗一部分能量，从而达到消声目的[16-18]。为尽量减小对隧道阻塞比的影响，腔体紧贴隧道内壁设置。谐振腔传播模型如图2（c）所示，连接管横截面积S、连接管长度L、腔室体积V 等参数决定了腔室的固有频率（连接管直径d=0.56 m，对应横截面积S=0.25 m2；连接管长度L=0.4 m），不同的腔室体积V 对应不同的固有频率。对2 种方案的谐振腔阵列结构进行数值模拟对比：方案1 采用不同腔室体积混合组合，腔室体积V 范围在17.9～111.9 m3之间；方案2 采用相同的腔室体积（V=36.5 m3）。2 种方案下，400 m 长度隧道内的腔体数量分别为28 和47 个。

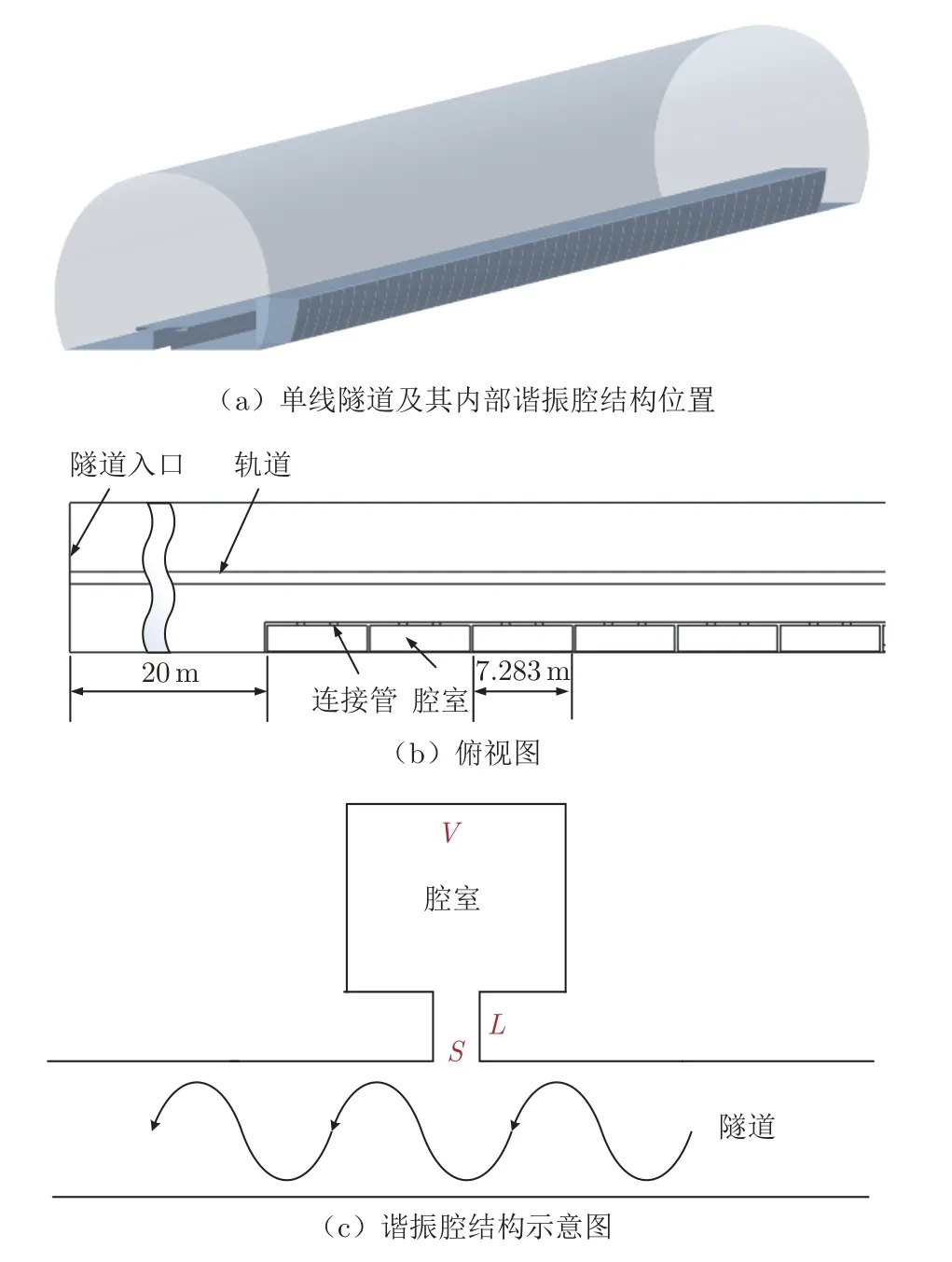
图2 隧道内谐振腔结构Fig.2 Resonators in the tunnel

1.2 计算域及边界条件

采用对流场进行分区的重叠网格法来模拟高速磁浮列车通过隧道产生的压力波问题。将计算区域划分为背景区域（包含整个求解域）和重叠区域（包含运动对象），实现列车与隧道的相对运动和数据交互，其精度和可信度在列车空气动力学研究中已得到认可[19-20]。列车驶入隧道前流场充分发展，隧道出、入口大气区域长度设为250 m，车头距离隧道入口约100 m，如图3 所示。计算域大气外场出、入口设置为无反射边界条件，车体设置为无滑移壁面边界条件。

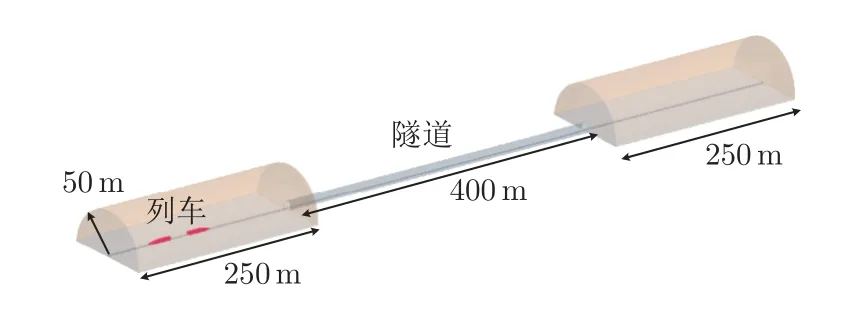
图3 计算区域Fig.3 Computational domain

1.3 网格划分

在商业软件STAR-CCM+中，采用Trimmed网格对计算区域进行体网格划分（图4）。车体面网格尺寸为0.05 m，表面设置为无滑移壁面，壁面边界层设置为10 层，增长比1.2，第一层网格厚度y+在100～150 之间。对列车和隧道的运行空间及隧道内谐振腔结构进行网格细化，体网格总量约3 500 万。

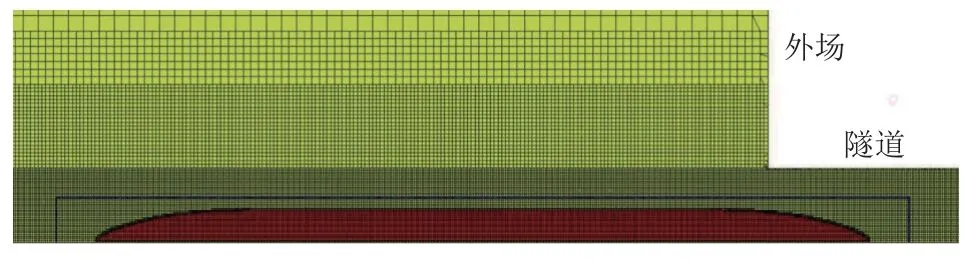
图4 计算模型体网格Fig.4 Volume mesh of simulation model

采用三维、非定常、可压缩N-S 方程和SST k-ω 湍流模型进行流场求解，时间步长0.001 1 s，每个计算步内迭代15 次。

1.4 测点布置

为研究谐振腔结构对隧道内压力波和隧道出口微气压波的影响，在隧道一侧壁面和隧道出口位置设置测点。在隧道内壁面每隔50 m 设置一个压力测点，如图5 所示，测点（P1～P7）高度相同（距离地面4 m）。参考微气压波的行业评判标准，微气压波测点布置在隧道出口外10、20 和50 m 处。

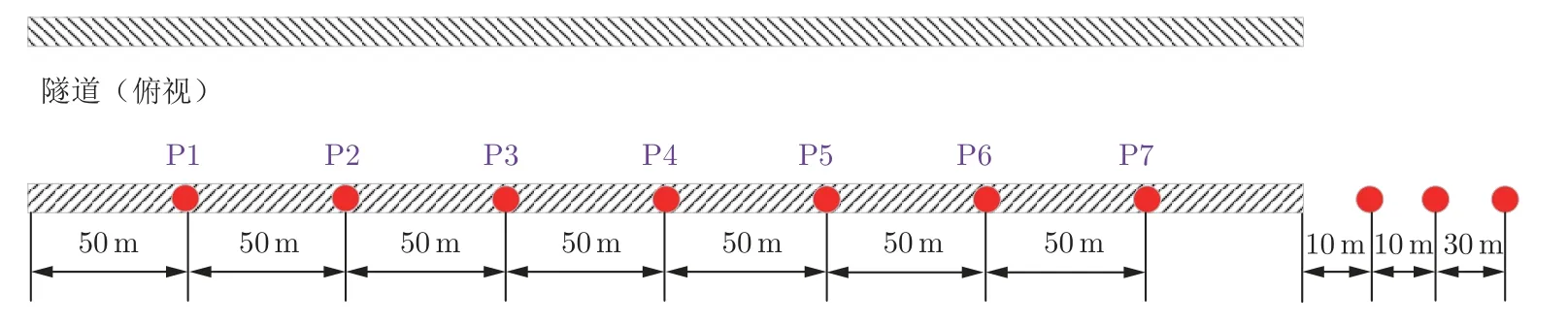
图5 隧道内壁面压力测点和隧道出口微气压波测点示意图Fig.5 Distribution of monitoring points on tunnel wall and at the entrance

2 数值模拟结果

2.1 不同结构下的压力波特性

图6 为高速磁浮列车以600 km/h 的速度通过400 m 隧道时，隧道中部测点P4 的压力波动曲线。为分析高速磁浮列车通过隧道的整个过程，图中给出了头尾车进入隧道产生的压力波特性和头尾车运行轨迹，其中黑实线表示压缩波（斜率为声速），黑虚线表示膨胀波（斜率为车速）。列车在t=0.623 s 到达隧道入口，产生压缩波，以当地声速传播至隧道中部测点P4，测点压力开始增大；在列车车体进入隧道过程中，测点压力持续增大；t=1.698 s，尾车进入隧道产生的膨胀波以当地声速到达该测点，测点压力开始下降；之后列车通过该测点，隧道壁面压力持续下降。在隧道内安装谐振腔装置后，车体进入隧道过程中的阻塞比增大，导致隧道壁面压力幅值增大，如方案1 的B 点所示，由8 235 Pa 增大至8 750 Pa，增大了6.25%。方案1 和2 对阻塞比的影响相同，2 种方案隧道壁面压力波正峰值分别为8 750和8 787 Pa，负峰值分别为9 159 和9 011 Pa，峰值变化率 ＜ 2%。

图6 不同方案下隧道内壁表面压力波特性Fig.6 Propagation characteristics of pressure waves in different schemes

2.2 不同结构下的微气压波特性

表1 为2 种方案下隧道出口不同距离处的微气压波幅值。可以看到，列车以600 km/h 的速度通过80 m2单线隧道时，在隧道出口外20 和50 m 处产生的微气压波幅值分别为898 和387 Pa。在方案1 下，20 和50 m 处的微气压波幅值分别为589 和259 Pa，分别减缓了34.41%和33.07%，平均减缓率为33.74%。在方案2 下，20 和50 m 处的微气压波幅值分别为522 和232 Pa，分别减缓了41.87%和40.05%，平均减缓率为40.96%。在2 种方案下，谐振腔结构均对隧道出口外的微气压波现象有明显的减缓作用，且在相同隧道长度条件下，方案2 效果优于方案1。

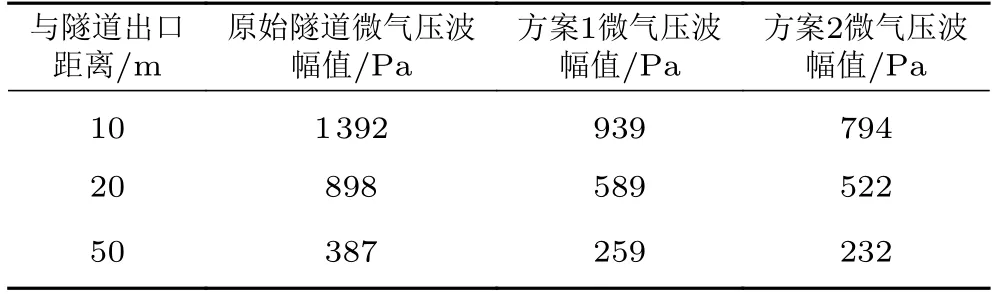
表1 不同方案下的微气压波幅值Table 1 Amplitudes of tunnel portal micro-pressure waves in different schemes

图7 为隧道内初始压缩波的压力梯度变化曲线。隧道内初始压缩波在传播过程中，波前压力梯度逐渐增大。在隧道内安装谐振腔结构之后，声波在隧道内传播，一部分能量传入谐振腔结构的连接管和共振腔体，连接管和共振腔体吸收和消耗部分声波能量，减缓了初始压缩波在传播过程中压力梯度的增大，进而减缓了隧道出口外的微气压波幅值。

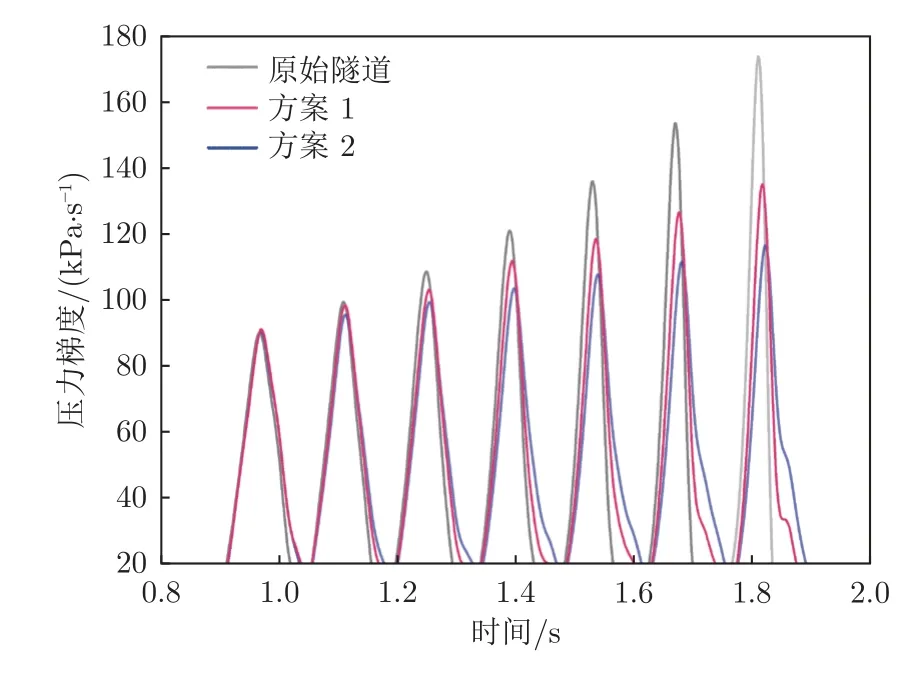
图7 隧道内初始压缩波的压力梯度变化曲线Fig.7 Pressure gradient curve of initial compressive wave in the tunnel

2.3 谐振腔数量对微气压波的影响

图8 为不同谐振腔数量（7、14、21 和28 个腔体）时，隧道出口外20 和50 m 处微气压波的减缓效果百分比（腔体均从隧道入口端开始布置）。可以看

图8 不同谐振腔数量对隧道出口微气压波的减缓效果Fig.8 Alleviative effect of different number of resonators on the micro-pressure wave at the tunnel exit

3 动模型试验验证

出，腔体数量越多，微气压波减缓效果越好。对腔体数量-微气压波减缓效果进行曲线拟合，可以看到微气压波减缓效果与腔体数量成线性关系，拟合曲线相关性指数R2为0.999 6。

3.1 试验方法

采用动模型试验方法对数值模拟优选隧道谐振腔结构方案2 进行试验验证。本次动模型试验在中南大学轨道交通安全教育部重点实验室的动模型试验平台进行（该平台获得了CNAS 资质认证[21]）。如图9 所示，该平台采用高压空气加速系统和分级逐步机械制动系统，全长164 m，分为加速段、匀速段和减速段。1∶20 模型车在加速段通过弹射从静止进行加速，达到预定试验速度后，进入匀速段并通过隧道，然后在减速段进行减速，在较短距离内安全停车。测试设备全程采集数据，并取匀速段的试验数据进行分析处理。

图9 动模型试验平台系统Fig.9 Moving model rig system

3.2 结果对比分析

列车模型以600 km/h 速度单车通过原始隧道和方案2 隧道，隧道壁面压力波动和隧道出口微气压波幅值与数值模拟结果对比如图10 所示。数值模拟与动模型试验的隧道壁面压力时程曲线一致性较好，在原始隧道内，隧道测点压力波动峰值最大误差为5.22%，在方案2 下，最大误差为4.82%。将隧道出口外20 和50 m 处微气压波幅值的数值模拟与试验结果进行对比，可以发现：在原始隧道中，隧道出口微气压波最大误差为9.1%，在方案2 下，最大误差为9.7%，均在10%以内。试验结果表明，所采用的数值模拟方法能够准确模拟列车通过隧道时的气动效应，隧道内谐振腔结构对隧道出口微气压波减缓效果明显。

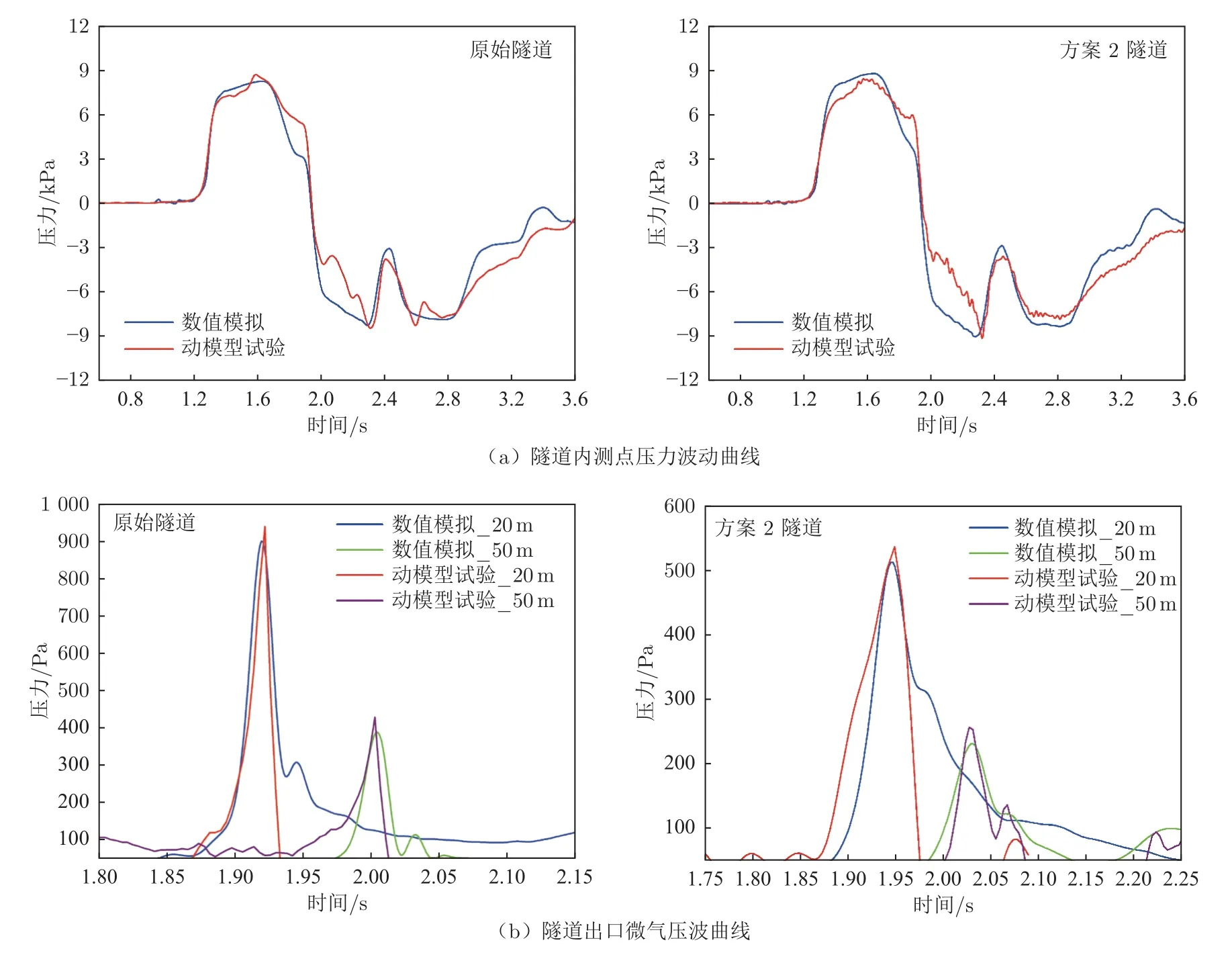
图10 动模型试验和数值模拟结果对比Fig.10 Comparison of moving model rig test and numerical simulation results

3.3 不同速度条件下的微气压波

采用动模型试验方法对比500、550 和600 km/h这3 个速度条件下，原始隧道与方案2 隧道出口外20 m 处微气压波减缓情况，结果如图11 所示。可以看到，方案2 隧道出口的微气压波幅值在3 个速度条件下均减小，减缓效果分别为39.7%、33.5%和22.3%。减缓效果与列车速度正相关：列车速度越高，减缓效果越明显。

4 结 论

采用数值模拟与动模型试验相结合的方法研究了隧道内谐振腔结构对高速磁浮列车通过隧道的气动效应减缓特性的影响。主要结论如下：

1）在隧道冗余空间内安装谐振腔结构使得隧道净空截面积变小，阻塞比增大，隧道表面压力增大。当列车以 600 km/h 速度通过 80 m2单线隧道时，隧道中部壁面最大压力幅值8 750 Pa，比原始隧道增大了6.25%。

2）谐振腔结构明显耗散了压力波的能量，减缓了初始压缩波在传播过程中压力梯度的增大。在列车速度600 km/h 条件下，隧道出口外20 和50 m 处微气压波幅值的平均减缓率为40.96%，但仍超出国家标准要求。建议采取在隧道出口加缓冲结构、竖井结构等多种措施进一步减缓微气压波。

3）谐振腔结构减缓效果与谐振腔参数和数量有关。在隧道长度为400 m 的条件下，微气压波减缓效果与腔体数量成线性关系。不同速度条件下，微气压波减缓效果与列车速度正相关。