基于CFD-DEM算法的压裂支撑剂缝内铺砂规律*

郭慧娟 高畅 韩金井 范应璞 Guodong Zhan 王宏伟 张金亚

(1.中国石油集团工程技术研究院有限公司 2. 中国石油大学(北京)机械与储运工程学院 3. 中国石油集团川庆钻探公司井下作业公司 4. Saudi Aramco Drilling Technology Division EXPEC Advanced Research Center)

0 引 言

近年来，随着页岩气、致密气的大规模开发，水力压裂技术成为油气资源增产稳产的关键技术[1-3]。该技术在储层压裂后井下压力小于闭合压力时，支撑剂保持裂缝张开形成高渗流通道，进而实现生产，是目前低渗透油气藏、页岩气藏实现开发的有效手段和利器。但由于当前现场施工条件以及成本限制，采用的传统支撑剂与压裂液使得支撑剂颗粒在输送至目标距离前就大量沉积在近井地带[4]，裂缝有效支撑距离短，开发效果不理想。因此，研究支撑剂在压裂缝内铺砂规律的影响具有重要意义。

目前，很多学者对支撑剂在裂缝内的沉降运移规律进行研究[5-8]。L.R.KERN等[9]对单一流速下支撑剂在水中流动首次进行了试验，发现了携砂液速度、支撑剂浓度以及支撑剂粒径大小具有函数关系。R.E.BABCOCK等[10]在L.R.KERN研究的基础上，针对牛顿流体与非牛顿流体流体进行物理试验，结果表明支撑剂浓度是裂缝高度的连续函数。张涛等[11]采用CFD数值模拟的方法，建立双欧拉两相流模型，研究了清水压裂中不同进口速度及位置，砂砾密度的支撑剂沉降行为，考虑了流动的湍流效应、高质量分数下颗粒间的摩擦应力。任岚等[12]采用有限体积法求解，分析了支撑剂密度为1 300与2 600 kg/m3在复杂裂缝中沉降运移行为，并分析了在分支裂缝阻力效应下多种因素对于支撑剂运移的影响。梁莹等[13]采用线性拟合的方法对低密度支撑剂在3种不同黏度压裂液下，不同排量和不同砂比砂堤的铺置形态进行拟合，应用于现场试验并具有良好的指导作用。ZHANG G.D.等[14-15]采用耦合EDEM与Fluent的方法，对比了多尺寸颗粒相对于均尺寸颗粒对支撑剂放置的影响，得出不同粒径的支撑剂形成的不同沙丘形态流场产生影响。WANG X.Y.等[16]研究裂缝闭合、注入速度和入口不均匀打开对单个裂缝中支撑剂分布的影响，以及支撑剂直径、密度和射孔高度差对支撑剂分选的影响。ZENG J.S.等[17-18]用CFD-DEM耦合研究支撑剂颗粒在交叉裂缝中的运移机理，考虑不同裂缝交角以及颗粒聚团效应，发现支撑剂进入支缝的比例与裂缝交角呈负角相关，在狭缝中会出现支撑剂非均匀聚团现象。支撑剂运移的本质问题是流体与固态颗粒的复杂耦合传动问题。基于计算流体力学建立的支撑剂运移模型大都采用欧拉框架，将流体-颗粒系统假设为互相掺混的2个流体组成的系统，要求固液两相均为连续相[19-20]，适用于颗粒质量分数低于10%的情况，且忽略了颗粒体积对流场的影响，对支撑剂在压裂缝中动力学表征较为有限。

为此，笔者采用计算流体力学-离散元(CFD-DEM)耦合方法对矩形压裂缝中颗粒的运移进行数值计算，采用单一因素控制变量法探究支撑剂密度、携砂液流速、质量分数以及压裂液黏度等因素对压裂缝支撑剂运移的影响规律，以期为选择合适的携砂液及泵注排量提供理论依据。

1 模型与网格

本文将输送模型简化为矩形，建立中等矩形裂缝的三维模型，采用计算流体力学-离散元(CFD-DEM)耦合方法对支撑剂的运移展布进行数值模拟。建立的三维几何模型如图1所示。图1中几何模型为长3 000 mm、宽6 mm、高600 mm的单一矩形平板裂缝。数值模型参考了可视化沉降试验的平板裂缝，左侧为3个均匀分布的入口，大小为60 mm×6 mm (顶部入口中心距离上壁面50 mm，底部入口中心距离下壁面50 mm，中部入口位于壁面正中间)，右侧出口大小为40 mm×6 mm，模型采用Gambit进行结构性网格划分，长度方向上网格数目为600个，高度方向上网格数为120个，宽度方向上网格数为2个，网格数量总计144 000个。假设流体为不可压缩牛顿流体。颗粒为规则的圆形颗粒，球体不发生形变且与流体在入口处充分均匀混合。

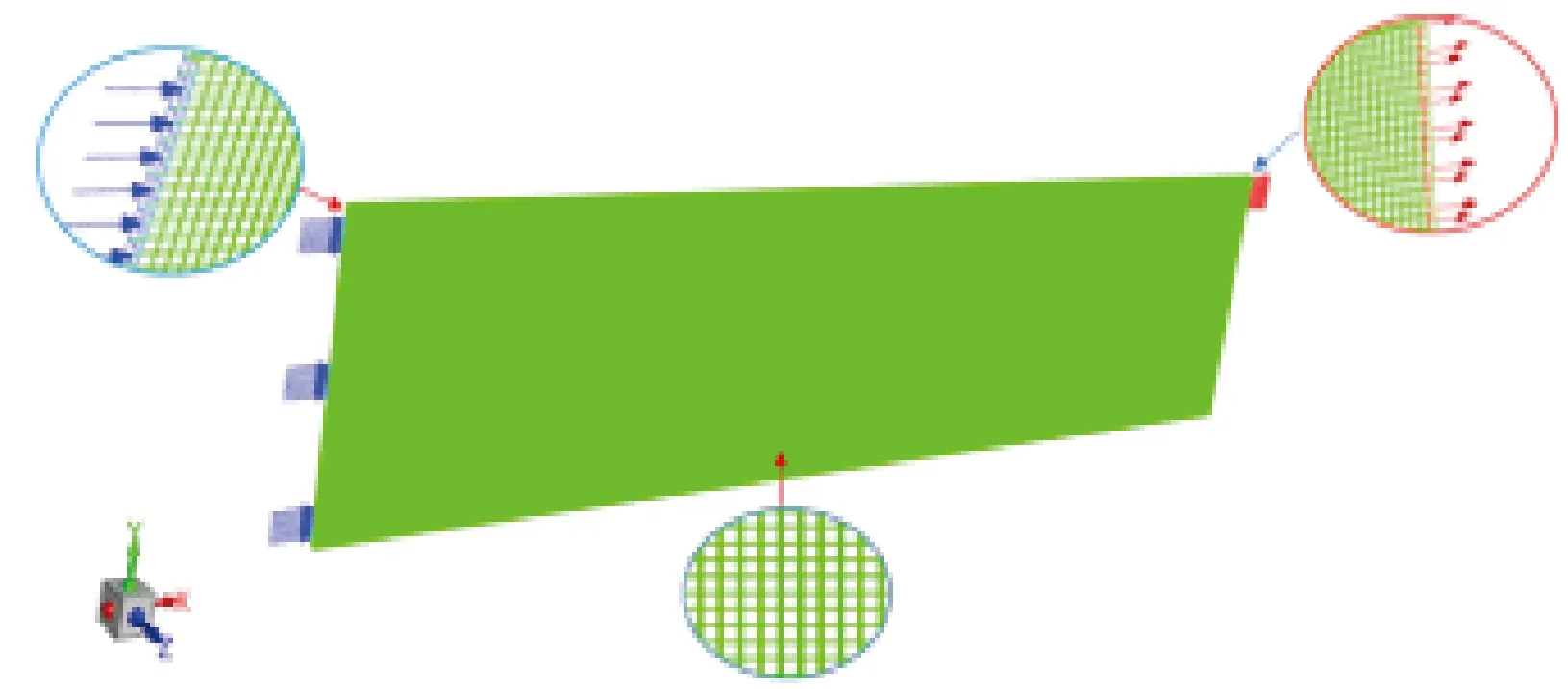
图1 三维几何模型示意图Fig.1 Schematic diagram of the 3D geometric model

2 数值模型与求解方法

在支撑剂运移的数值计算中，不仅要考虑颗粒运动对流体的影响，也要考虑流体对颗粒的反作用力。压裂缝中流体流动控制方程为质量守恒及动量守恒方程，采用k-ε湍流模型使连续相计算方程组封闭，颗粒相采用EDEM中的单颗粒平动方程、转动方程及固液相间作用力模型。

2.1 连续相控制方程

2.1.1 质量守恒方程

流体相的运动由Navier-Stokes方程控制，方程如下：

(1)

(2)

式中：ρ为流体的密度，kg/m3；εl为流体体积分数；ul为流动速度，m/s；k为流体相湍动能，m2/s2；ε为湍流耗散率，m2/s3；t为时间，s；Gk为湍动能产生相，kg/(m·s3)；μt为湍流黏度，Pa·s；μ为液相动力黏度，Pa·s；σk为湍动轮k对应的Prandtl数，σk=1.0；ui为X方向速度分量。

2.1.2 动量方程

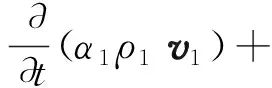
-α1∇p1+∇τ1+α1ρ1g+β(vs-v1)

(3)

τl=μ(∇u+∇uT)

(4)

式中：p1为流体压力，Pa；g为重力加速度，g=9.81 m/s2；τ1为剪切应力张量，Pa；β为相间动量交换系数，kg/(m3·s)；α1为动量修正系数；vs为出口流速，m/s；v1为入口流速，m/s；u为时均速度，m/s。

2.1.3 湍流方程

本文采用Realizablek-ε模型，在应变率大的情况下，会产生正应力小于0的情况，该模型对正应力进行了数学修正。

Gk+Gb-ρε-YM

(5)

湍流扩散方程：

(6)

式中：σε为湍动能ε对应的Prandtl数，σε=1.2；Gk、Gb、YM参数与标准化k-ε模型相同，Pa/s；C1ε、C3ε、C1、C2、A0为经验常数；ak为修正系数；Meff为液体动力黏度，Pa·s；E为时均应变率，s-1；v为液体流速，m/s。

2.2 颗粒相控制方程

2.2.1 单颗粒受力方程

Fk=FD+FVM+FL+Fg+FF

(7)

式中：FF为浮力，N；Fg为重力，N；FL为升力，N；FVM为虚拟质量力，N；FD为拖曳力，N。

2.2.2 单颗粒平动方程和转动方程

EDEM通过跟踪单个颗粒轨迹来预测固相行为，颗粒的运动遵循牛顿第二定律。

平动方程：

(8)

转动方程：

(9)

式中：mp，i为颗粒i的质量，kg；up，i为颗粒i的线速度，m/s；Fpc，ij为颗粒i与其他颗粒接触产生的接触力，N；Flp，i为流体对颗粒i的作用力，N；Ipc，ij为颗粒i的转动惯量，kg·m2；ωp，i为颗粒i的角速度，rad/s；Tpc，ij为颗粒i与颗粒j接触产生的接触力矩，N·m。

(10)

2.3 两相相间耦合模型

在固液两相流动中，颗粒受到液体的多种力，这里主要考虑浮力和拖曳力。

2.3.1 固液相间作用力模型

浮力为：

(11)

拖曳力为：

(12)

(13)

虚拟质量力：

(14)

升力为：

FL=CLαsρl(ur)×(∇×ul)

(15)

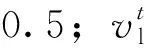
2.3.2 液相对固相的曳力模型

液相对固相的曳力计算采用Gidaspow模型，该模型是基于Ergum模型和Wen&Yu模型得到的经验模型，适用于稠密的流化床模拟。其中εl代表液体体积分数，当液体体积分数小于0.8时，颗粒雷诺数对曳力无影响；当液体体积分数大于0.8时，颗粒雷诺数对曳力产生影响。

(16)

(17)

(18)

式中：Rep为颗粒雷诺数，无因次；εs为固相体积分数。

2.4 边界条件与求解方法

上述控制方程采用有限体积法求解，湍流模型采用Realizablek-ε模型，强化壁面湍流，边界设置为速度入口，压力出口0.1 MPa，支撑剂泊松比0.5，静摩擦因数0.5，动摩擦因数0.08，颗粒直径1 mm，无滑移壁面条件，采用SIMPLE算法求解速度与压力的耦合，设置DEM的时间步长2×10-5s，模拟时长20 s。

3 模拟方法验证

为了验证流固耦合模型的准确性，对试验流速为0.64 m/s时支撑剂运移的模拟结果与韩琦[21]的平板裂缝沉降试验结果进行对比(见图2)。试验装置为大型可视化单一平板裂缝模型，对比参数如表1所示。

图2 试验流速0.64 m/s试验模拟对比图Fig.2 Experimental and simulation results at the flow rate of 0.64 m/s

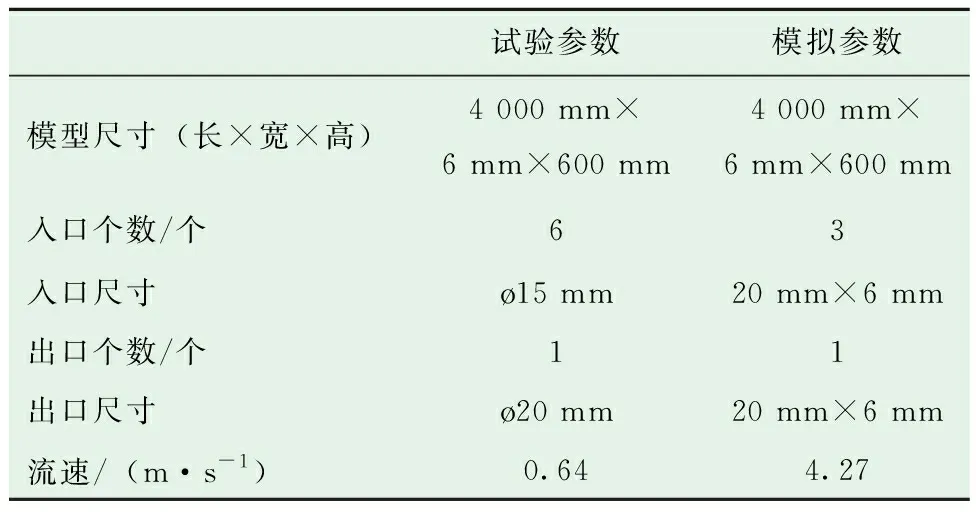
表1 试验模拟对照参数表Table 1 Experiment and simulation parameters

由图2可以看出，砂堤整体呈现出“两段状”(由于计算资源受限，模拟计算时间为30 s)，两段砂堤的中间部分沉降床高度与计算时间呈正相关，逐渐呈现出从“2个砂堤→1个砂堤”的趋势。试验主砂堤的位置约为2.15 m处，模拟时主砂堤的位置约为1.75 m处。分析砂丘位置产生差异的主要原因是仿真时采用颗粒直径为1 mm进行计算，而试验时采用1～2 mm混合直径支撑剂，造成初始堆积位置的差异。可以看出支撑剂的运移沉降行为试验与模拟情况较为相符，证明所建立流固耦合模型的准确性。

4 模拟结果分析

4.1 支撑剂密度对运移规律的影响

在携砂液黏度为1 mPa·s，射流速度为1.6 m/s，颗粒质量分数4%工况下，分别对3种密度的支撑剂进行模拟，结果如图3所示。

本文用携砂液传输末端质量分数梯度角α来评价支撑剂的运移情况，传输末端质量分数梯度角α表示传输末端携砂液质量分数沿流动方向的变化速率。由于入口的射流作用，携砂液在入口处呈现“弹状流”状态，流场扰动较大。随时间推移携砂液裂缝中流动，流场逐渐平缓，此时支撑剂的受力情况较为稳定，传输末端质量分数梯度角α越大，表明沉降床铺置更均匀且至裂缝深处，输砂行为整体更接近于活塞流。由图3a可知：高密度支撑剂(2 850 kg/m3)由于重力的对流作用在入口处迅速发生沉降，砂堤整体长度为1.50 m，传输末端质量分数梯度角α急剧变小；中密度支撑剂(1 950 kg/m3)在距离入口0.15 m处发生沉降，砂堤整体长度为2.15 m，传输末端质量分数梯度角α接近150°；低密度支撑剂(1 190 kg/ m3)在距离入口0.30 m处发生沉降，运移至裂缝最末端，在裂缝中铺置更均匀，传输能力更强。随着注入时间的延长，沉降床的高度稳定提升，传输末端质量分数梯度角α为平角。

图4为不同密度支撑剂的液相体积分数分布图(图4a、图4b、图4c体积分数分别是24.6%、27.3%、32.8%)。较之高体积分数支撑剂，中低密度支撑剂的流化区域更大，且在沉降床表层流化度更高，表明支撑剂的密度越小，支撑剂堆积越松散，运移性能越好。

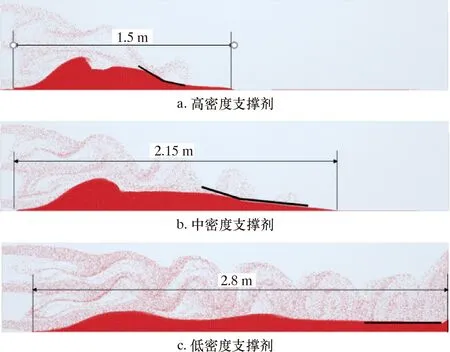
图3 不同密度支撑剂运移图Fig.3 Migration of proppants with different densities

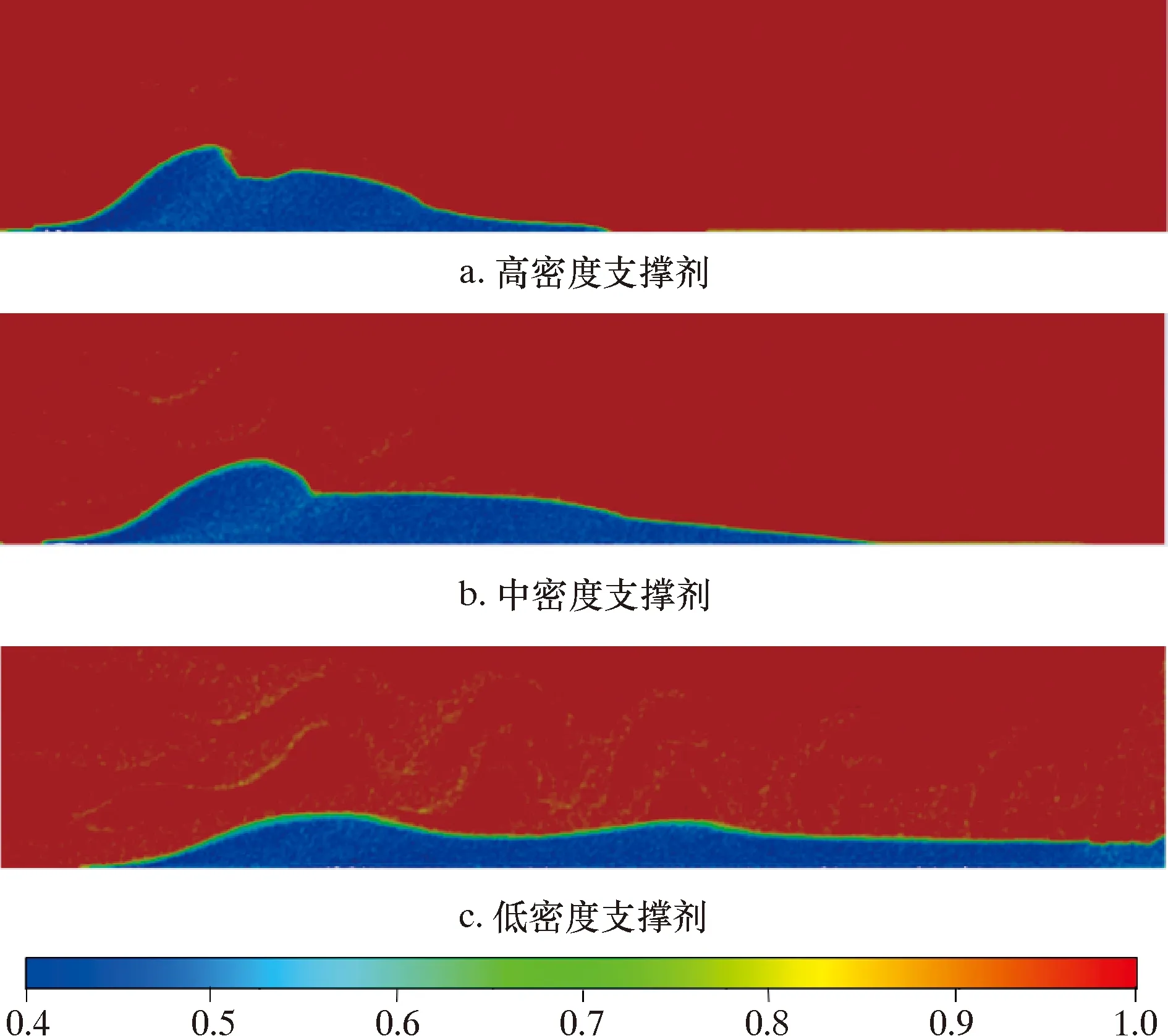
图4 不同密度支撑剂液相体积分数分布Fig.4 Liquid phase volume fraction distribution of proppants with different densities

图5为3种密度支撑剂不同时刻的运移过程图。高密度支撑剂(见图5a)在入口处迅速沉降，随着混砂液向前推进，液体的动能逐渐耗尽，支撑剂曳力小于重力，在注入时间为5 s时，在入口附近支撑剂沉降和堆积为3个小沙丘。随着注入时间延长至10 s时，整体表现为沉降床高度逐渐增高，砂堤形态并无明显变化。注入时间15 s时，砂堤高度增长速度变快，在越过第一个沙丘后，流过沉降床上方的携砂液流速变大，注入的颗粒逐渐向沙丘背侧堆积，因此沙丘形态逐步由3个沙丘变为2个沙丘，之后延长注入时间只沿沉降床高度方向变化。中密度支撑剂(见图5b)在距离入口0.15 m处发生沉降，随着携砂液向裂缝深处运移，沉降床逐渐由2个沙丘合并为1个“驼峰式”沙丘。低密度支撑剂(见图5c)由于湍流作用，支撑剂在出口被“吸出”，支撑剂沉降床无明显沙丘。

图5 3种密度支撑剂的不同时刻的运移过程图Fig.5 Migration process of proppants with three densities at different time

4.2 携砂液黏度对运移规律的影响

在支撑剂密度为1 190 kg/m3，射流速度为1.6 m/s，颗粒质量分数4%工况下，分别对携砂液黏度为1、2、3 mPa·s进行模拟。图6为不同黏度压裂液的运移规律对比图。由图6可知，由于液体黏度升高，颗粒的随附性变强，大量支撑剂随压裂液在出口流出，沉降颗粒变少，所以高黏度压裂液较之中低黏度压裂液的沉降床高度变低，同时液体的湍流强度变弱，具体体现为悬砂区的“波纹”情况逐渐减缓。说明支撑剂的运移性能随着压裂液的黏度增加而逐渐变好。在裂缝最末端支撑剂沿壁面向出口延伸，砂丘高度逐渐变高。当液体黏度为1 mPa·s时，最小体积分数为24.6%，而液体黏度为2和3 mPa·s时最小体积分数均为19%。这说明当液体黏度增加至一定程度时，支撑剂的悬浮性能达到极限，继续增加压裂液的黏度并不会对支撑剂的悬浮性能产生积极的影响，反而影响支撑剂的返排，对地层产生伤害。

图6 不同黏度压裂液支撑剂运移图Fig.6 Proppant migration under different fracturing fluid viscosities

4.3 支撑剂流速对运移规律的影响

在携砂液黏度为1 mPa·s，支撑剂密度为1 190 kg/m3，颗粒质量分数4%工况下，分别对现场施工排量为7.0、4.0、2.5 m3/min进行模拟。对应的模拟速度如表2所示

表2 现场施工排量与模拟速度对比表Table 2 Comparison ofon-site pump rate and simulated flow rate

图7为不同流速支撑剂的运移规律图。由图7可知：速度为1.60 m/s时，支撑剂在距离入口0.3 m时就会发生沉降，颗粒主要堆积在中部靠近入口一侧；速度为2.67 m/s时，支撑剂在距离入口0.9 m处发生堆积，颗粒主要堆积在中部靠近出口侧，由于尾部沉降床高度增高，支撑剂的出口速度逐渐变大，输砂区的面积较大且整体湍流强度更强；速度为4.27 m/s时，支撑剂沉降堆积在出口附近，运移状态发生明显改变，由于动能较大，输砂区表现为整体横向运移，携砂液流动接近于活塞流，在出口被“吸出”。

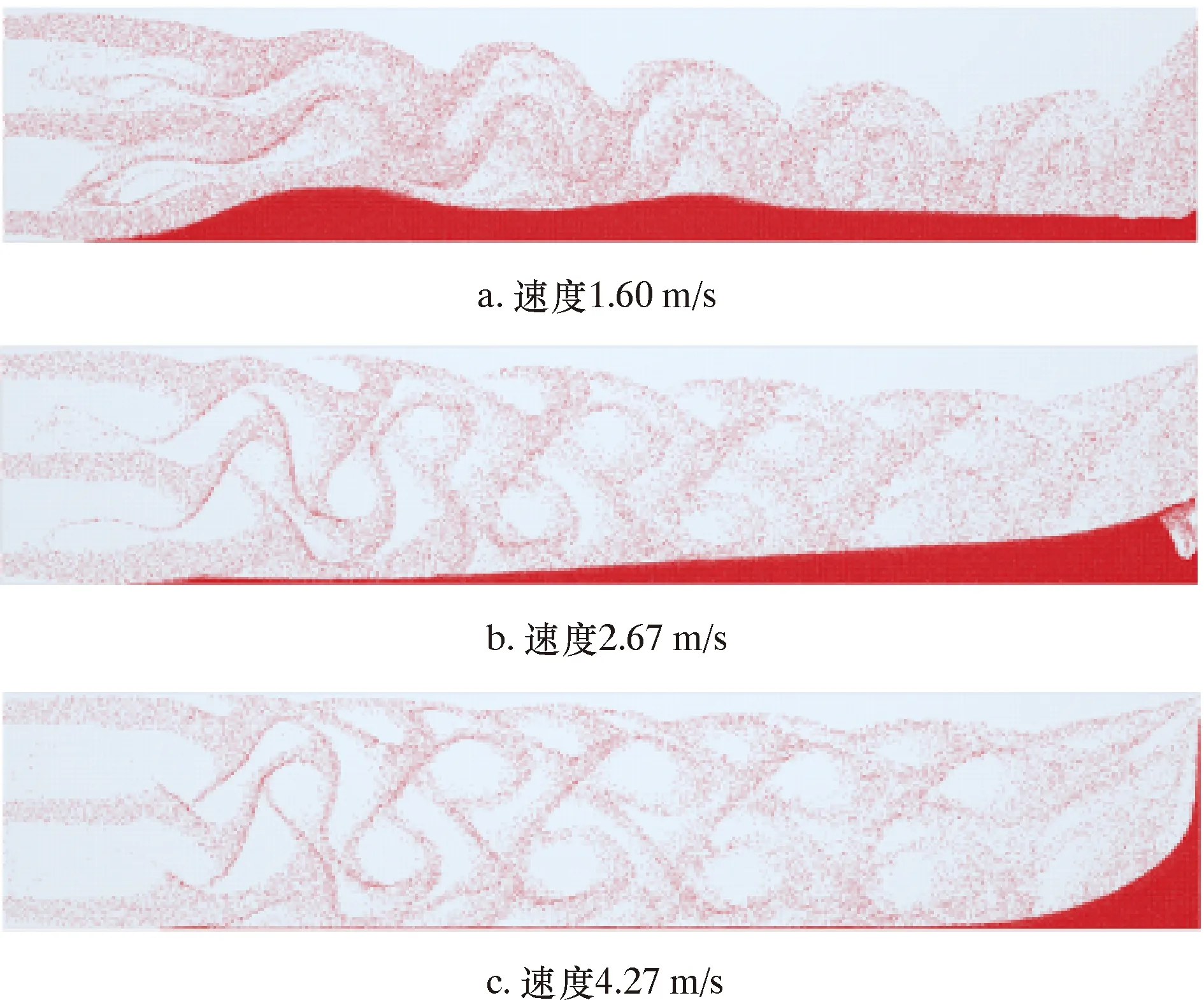
图7 不同流速支撑剂的运移规律图Fig.7 Proppant migration at different flow rates

4.4 支撑剂颗粒质量分数对运移规律的影响

在支撑剂密度为1 190 kg/m3，携砂液黏度为1 mPa·s，射流速度为1.6 m/s工况下，分别对颗粒质量分数为4%、6%、8%、10%的工况进行模拟，结果如图8所示。

由图8可以看出，颗粒质量分数与沉降床高度呈正相关性，相比图8a与图8b的沉降床高度增长，图8c与图8d的增长幅度减缓。随着砂比的继续增加，支撑剂扰动效应使得支撑剂增加速率下降，支撑剂沉降床的高度逐渐接近支撑剂的“平衡高度”，携砂液的流速也逐渐增大至“平衡流速”，相当于增加了输砂液的流速，使得沉降的支撑剂变少，悬浮态支撑剂明显增多，支撑剂高度增加逐渐减缓。当沉降床砂堤高度达到“平衡高度”时，支撑剂的重力与浮力达到平衡，不会继续沉降。颗粒质量分数6%、8%、10%对应流化区的液相体积分数分别为21.8%、24.6%、30.2%，证明支撑剂的沉降速度逐渐降低，高浓度支撑剂由于更为接近“平衡高度”。沉降床表面流化区域更大，一部分支撑剂由于堆积滑落至入口处产生堆积，长时间注入将堵塞入口，发生“卡泵”现象。

图8 不同颗粒质量分数支撑剂运移图Fig.8 Proppant migration under different particle concentrations

5 结 论

(1)同工况下，低密度支撑剂输送距离较中密度支撑剂提升30.3%，较高密度支撑剂提高86.7%，密度较低的支撑剂输送性能更好。在现场作业时，可以采取梯度密度支撑剂的注入方式，可以优先注入低密度支撑剂运送至裂缝深处，后期分别注入中高密度支撑剂对整个裂缝进行填充。

(2)一定程度上增加压裂液黏度，会使携砂液的湍流程度变弱，压裂液的携砂性变强，在实际压裂作业中，可采用高黏性压裂液将支撑剂携带到裂缝深处。

(3)较高的流速可以使支撑剂沉降距离入口越来越远，实际压裂作业时，可以考虑脉冲变速注入的方式，既可以防止入口堵塞，也可以保证一部分支撑剂在较高流速携砂液的带动下进入裂缝末端。

(4)适当提高支撑剂质量分数可以提前达到支撑剂沉降床高度，但质量分数过高的支撑剂会在入口出现堆积现象，混输泵工作时，容易引起“卡泵”现象。现场压裂作业时，要保证合理的注入浓度，也可以采取变速加砂和梯度混砂的方式避免堵塞情况发生，同时提高支撑剂的输送效率。