基于数论的纯整数规划问题的解法研究

周 斌

（三明医学科技职业学院，福建三明 365001）

整数规划（integer programming，IP）问题是一类要求问题的解中一部分或全部变量为整数的规划问题，是1958 年戈莫里提出割平面法后形成的独立分支〔1〕。整数规划问题是要求决策变量取整数值的线性规划（linear programing，LP）或非线性规划（nonlinear programming，NP）问题〔2〕。而纯整数规划（pure integer programming，PIP）问题作为整数规划问题的一种特殊形式，目前求此类规划问题比较成功又流行的方法是分枝定界法和割平面法〔3〕。分枝定界法的主要思路〔3〕是首先求解整数规划的伴随规划，通过添加约束的方法缩小可行域，使最优解符合整数条件〔4〕。割平面法有许多种类型，但思路基本相同，也是用增加新的约束条件来切割可行域，增加的新约束条件称为割平面方程，通过不断地切割缩小过程，最终得到整数最优解〔5〕。分枝定界法属于一种隐枚举法，对于自变量较多的情况，会存在“组合爆炸”的问题，难以适用〔6〕；而割平面法往往存在收敛速度很慢，甚至不收敛的问题〔7〕。此外，近年来还出现了许多智能算法，但智能算法往往无法保证它的收敛性，例如代数式恒等变形、不等式估算法、同余法、构造法、无穷递推法等〔8-9〕。然而这些运算方法均比较复杂，收敛速度比较慢。针对这个问题，利用不定方程与最优化模型的一些共性，根据解不定方程问题的不等式估算法，提出一种高效的纯整数规划问题的新解法。这种新解法与传统的纯整数规划问题的解法最大的不同点在于它不需要求解原规划问题所伴随的松弛线性规划问题，而仅需要进行一些简单的求解方程和代数运算。以纯整数规划问题为例子，分别用割平面法、分枝定界法和提出的新解法进行求解，验证本文提出新解法的可行性。

1 相关理论概述

1.1 纯整数规划问题算法思路

1.1.1 一般纯整数规划问题 一般纯整数规划问题的模型〔10〕为

其中，A 是m 行n 列矩阵，其元素全为整数；b 为m维列向量，其元素全为整数；C 是n 维列向量，其元素全为整数；X 是n 维列向量，其元素为非负整数。1.1.2 二维变量的纯整数规划问题 二维变量的纯整数规划问题的模型〔11〕为

其中，a11，a12，a21，a22，b1，b2，c1，c2全为整数。由于约束条件的限制，可以得出约束变量x1，x2的上限，而根据x1，x2的非负要求，又可以得出x1，x2的下限，即x11≤x1≤x1s，x21≤x2≤x2r。根据整数限制又可以得到x1∈［x11，x1s］，x2∈［x21，x2r］。由此，可以得出函数f（x1，x2）的取值只能是某个范围内的整数，通过x1，x2的取值范围，就可以确定f（x1，x2）的取值范围为f∈［fmin，fmax］。因此，可以添加一个约束条件到原整数规划问题中，从而缩小x 的可行域，减少计算量，以提高计算速度。则式（2）可转化为如下等价形式：

这也就是把可行域缩小到了原可行域与平面f＝c1x1+c2x2的相交处，然后让f 的值从fmax向fmin依次取整数，即从大到小开始取值。当到达第一个f 的值所对应的约束变量解组（x1i，x2j）（1≤i≤s，1≤j≤r）满足约束条件时，此时的约束变量解组（x1i，x2j）即为此纯整数规划问题的最优解组。而当所有的f 值所对应的约束变量解组（x1i，x2j）（1≤i≤s，1≤j≤r）都不满足约束条件时，则表示此纯整数规划问题无最优解。

1.2 相关定理及推论采用数论的常用记号，记（c1，c2）为c1与c2的最大公约数，（c1，c2，…，cn）为c1，c2，…，cn的最大公约数。

证明：记d=（c1，c2，…，cn），d 为一个整数，

定理2 f＝c1x1+c2x2+…+cnxn有整数解的充分必要条件为（c1，c2，…，cn）｜f，即c1，c2，…，cn的最大公约数能整除f。

证明：若f＝c1x1+c2x2+…+cnxn有一整数解，设为x10，x20，…，xn0，则f=c1x10+c2x20+…+cnxn0，但（c1，c2，…，cn）整除c1，c2，…，cn，因而整除f，从而条件的必要性得证。反之，若（c1，c2，…，cn）｜f，则f＝k（c1，c2，…，cn），k为整数，则存在n 个整数s1，s2，…，sn满足c1s1+c2s2+…+cnsn＝（c1，c2，…，cn）。令x10＝ks1，x20=ks2，…，xn0=ksn，即得c1x10+c2x20+…+cnxn0＝f，故f＝c1x1+c2x2+…+cnxn有整数解。

通过定理1 和定理2，就可以在不考虑x 的取值范围时，使f＝c1x1+c2x2+…+cnxn总有整数解，而且可以有效地过滤掉明显没有意义的f 值。

2 实例验证

在给出新解法的思路和步骤以及定理1、2 后，下面将用一些纯整数规划问题的具体算例来验证此解法，并通过与分枝定界法和割平面法的对比，验证此解法的优缺点以及它的适用性。现在对纯整数规划问题

分别用割平面法、分枝定界法和本文所提出的新解法来解决。

2.1 割平面法

（1）求解松弛问题

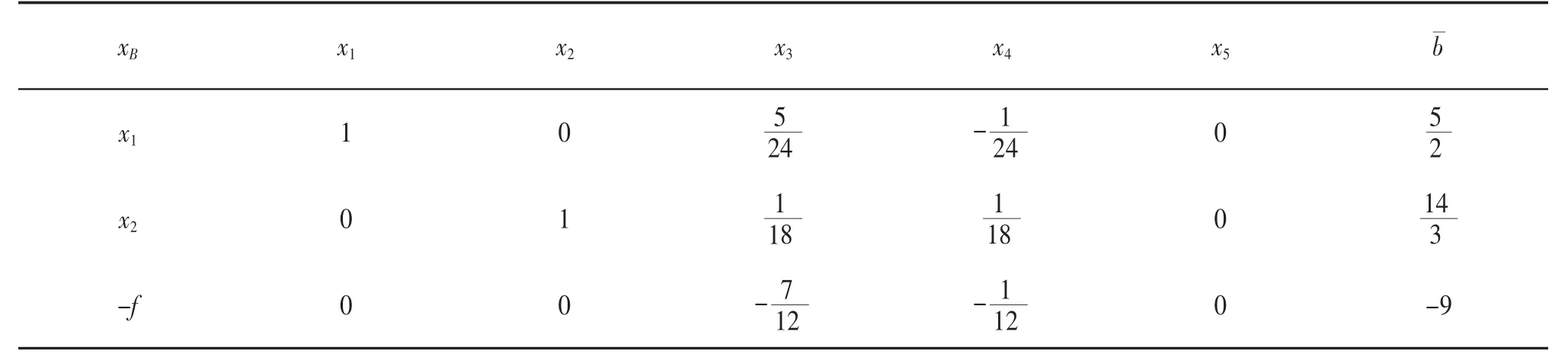
表1 迭代单纯形表

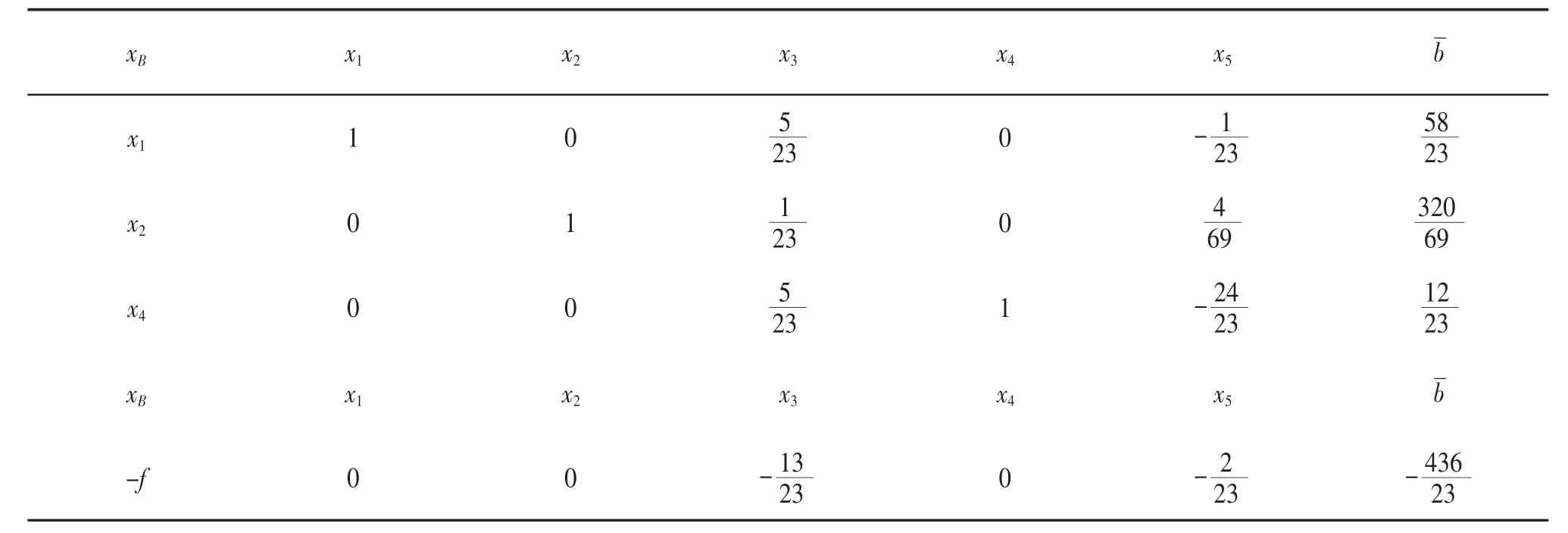
表2 迭代后的单纯形表

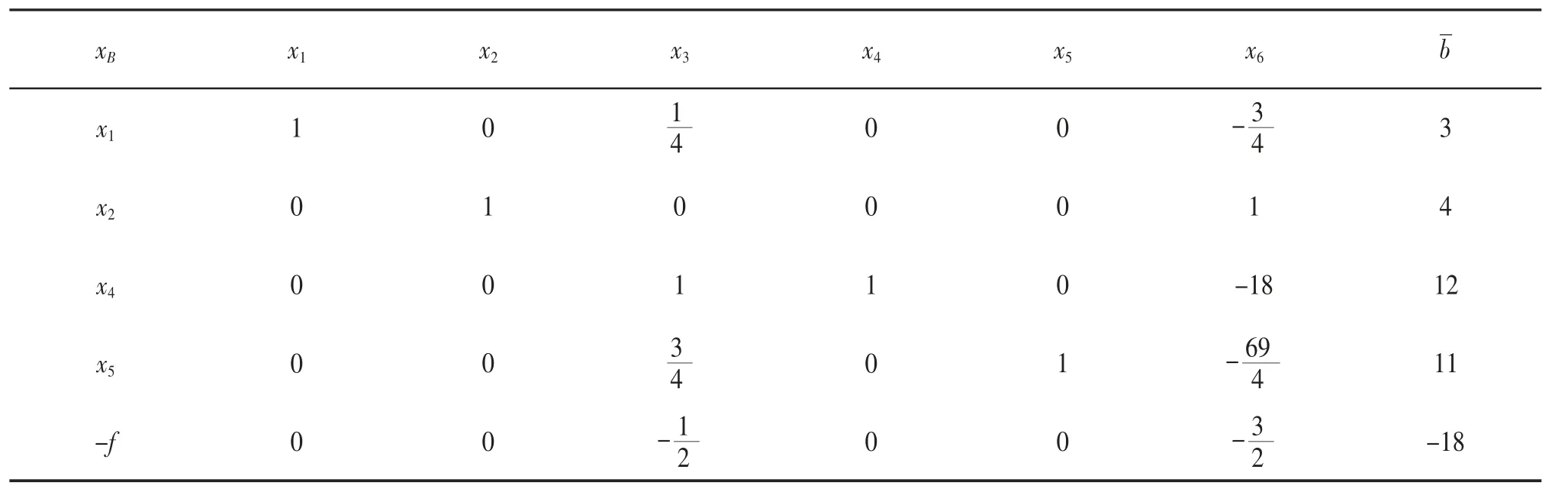
表3 再次迭代后的单纯形表

（2）求解割平面方程

2.2 分枝定界法

（1）求解松弛问题

图1 松弛问题式（4）的图解法

（2）分枝

因为式（4）的最优解x1，x2均非整数，取x1进行分枝，与最靠近的两个整数为2 和3，故构造两个约束条件x1≤2 和x1≥3。分别并入式（4）中得

两个子问题的可行域分别记为S1和S2，如图2，S1US2包含了纯整数规划问题的全部整数解，点A被排除在外。

图2 增加约束条件后的松弛问题图解法

（3）求解两个子问题的整数点，没有必要再对式（5-2）进行分枝搜索。全部分枝都已查清，原纯整数规划问题的最优解为点C，即X*＝（3，4）=18。

2.3 纯整数规划问题的新解法从约束条件可以得出x1与x2的取值范围x1∈［0，1，2，3，4，5，6］，x2∈［0，1，2，3，4，5，6，7，8］，记f＝2x1+3x2，根据x1与x2的取值范围，可以得出f 的取值范围为f∈［0，1，2，…，36］。由于是问题，故由f 的值从大到小开始验证，第一个满足约束条件的最优解组即为最优解。新解法计算流程图见图3。

图3 新解法计算流程图

从图3 得出，X*＝（3，4）即为最优解，=18。从整个求解的过程来看，用割平面法和分枝定界法都需要解原纯整数规划问题的一些伴随子规划问题。而就这个问题而言，用割平面法比其他两种方法要复杂得多，在求解子规划问题的同时，割平面法需要求解平面S 的平面方程，而分枝定界法则需要求解平面S1和S2的平面方程。而本文所提出的这种方法不但不用求解伴随的子规划问题，运算过程也比其他两种方法更简单，计算量也更小，它只是求解一些方程，进行一些等式解的验算。因而，在纯整数规划问题中，当维数不是很大或是f 的取值范围不是很广的情况下，本文所提出的方法所需要的计算量相比较而言要小得多，而且也比较简单。在求解的过程中也不会出现一些传统算法中必须解决的线性子规划问题，只要求做一些简单的方程求解与验证。对于维数较大或是f 的取值范围较广的纯整数规划问题，这种算法也同样适合，但也会像传统的算法一样，计算量大且烦琐，要验证的范围会比较大。因此在做的过程中要求很细心，要考虑到每一个可能的取值和解组。

3 结语

区别于传统的研究方法，从数论的角度来重新审视纯整数规划问题，利用数论中的不定方程理论，提出一种求解纯整数规划问题的新解法。此方法不但可以快速地发现并去掉没有意义的f 值以及相对应的最优解组，而且还不用解决任何的伴随线性子规划问题。因而这种结合了数论和最优化两种学科的方法对解决纯整数规划问题不但快速而且简单。在纯整数规划问题中，当f 的取值范围非常广或是维数很大的情况下，这种方法也可以用，但它更适用于一些f 的取值范围不是非常大或是维数不是很大的纯整数规划问题。