基于结构方程模型的疾病性状相关基因的识别*

牟红婷

（中国石油大学（华东）计算机科学与技术学院 青岛 266580）

1 引言

癌症、心血管疾病等复杂疾病是影响人们身体健康的一个重要因素。其发病率高，遗传方式不确定，致病机理异常复杂［1～2］。疾病性状是复杂疾病的表现特征，是疾病的特征标签，而且复杂疾病多表现为连续的数量性状变异，疾病性状很容易被量化。因此为了了解复杂疾病的发病机制，发现和疾病性状相关的基因非常重要，这对复杂疾病的诊断、治疗以及预防都起到至关重要的作用［3～4］。

复杂疾病并不只是由单个基因引起的，而是由多个基因共同决定，受多个基因共同影响。其中每个基因的作用相对较弱，但是它们的综合作用却可以产生显著作用。在分离分析每一个基因时，都有产生巨大假阳性的结果的可能性，因此我们很难发现相互作用的基因［5］。除此之外，人体中有数以万计的基因，如果对全部基因进行研究分析，无论是基因与基因之间的相互作用关系还是基因与疾病性状之间的相互作用关系都是庞大且复杂的，这对数据的选择工作也提出了新的挑战。

所以本文提出利用结构方程模型对基因和疾病相关性状建模，量化了多个基因的综合作用，以及多组基因和疾病相关性状的关联关系，发现与疾病性状相关的基因。结构方程模型可以用来解决多个变量之间的相互作用，明确量化单个变量对整体的作用和单个变量之间的作用［6～7］。与其他方法相比，结构方程模型所估计的参数更加准确，而且无需考虑控制变量；其次这种方法可以将测量误差排除在外。

2 材料和方法

2.1 数据

癌症的mRNA 表达谱数据和临床数据从基因表达Omnibus（GEO）（https：//www.ncbi）获得，我们对下载的数据进行了预处理，删除部分与实验不相关的数据，对缺失值进行删除或填补，以及对基因数据标准化等。最终获得肺癌数据（GSE103512、GSE74777）共176 例。临床数据都包括样本的年龄、肿瘤大小和肿瘤分期，以便识别和癌症性状相关的基因。

2.2 建立基因潜变量

利用结构方程模型对癌症基因和性状建模，但是无法对所有的基因建模，所以我们从全部的基因中筛选差异表达基因，建立基因潜变量。使用limma 包通过分析比较正常样本与疾病样本的基因归一化表达数据，筛选出表达最差异的部分基因。然后对差异表达基因进行分层聚类，把最相似的基因聚为一类。因子分析（factor analysis）［8］是一种用来探讨连续变量之间相关性的统计方法。利用因子分析来确定代表一组基因相互作用的共同影响，并用一个变量来代替，这个变量就是潜变量。因子分析的数学模型其实是联系潜在因子与可观测变量的一系列方程组。

xi是第i 个可观测变量。f是潜变量。λi是待估计的因子载荷，δi是各个观测变量的度量误差。

2.3 结构方程模型

结构方程模型即用变量的协方差矩阵来分析变量之间关系，模型中既包含有可观测的显在变量，也包含无法直接观测的潜在变量。结构方程模型包括两个部分：测量模型和结构模型。

测量模型一般由两个方程式组成，分别规定了内生的潜在向量η和内生的可观测变量Y之间，以及外生的潜在向量ξ和外生的可观测变量X之间的联系，即：

其中，ΛY表示Y对η的回归系数矩阵(p×m)，ε表示Υ的测量误差构成的向量(P×1) 。 ΛX表示X对ξ的回归系数矩阵(q×n)，δ表示X的测量误差构成的向量(q×1) 。

结构方程模型规定了所研究的系统中假设的潜在外生变量和潜在内生变量之间的因果关系，即

其中，B表示潜在内生变量对潜在外生变量的效应的系数矩阵(m×n)。Γ 表示潜在外生变量对潜在内生变量的效应的系数矩阵(m×n)，ζ表示残差项构成的向量(m×1) 。

为了确定模型参数，尽量减小模型中隐含的模型协方差矩阵与样本协方差矩阵之间的差距，采用最大似然法，通过拟合得到矩阵方程中所有自由参数的值。

3 结果

3.1 数据预处理

因为基因数目庞大，所以只利用其中一部分基因来进行试验分析。为了选取基因，使用limma 包通过分析比较正常样本与疾病样本的归一化表达数据，来识别差异表达基因，结果如图1 所示。选取最差异的前70 个基因为一组命名为S1，选取中间70 个基因为S2，最不差异的70 个基因为S3。分别利用结构方程模型进行分析每组基因，比较并讨论它们与疾病相关性状之间的关系。

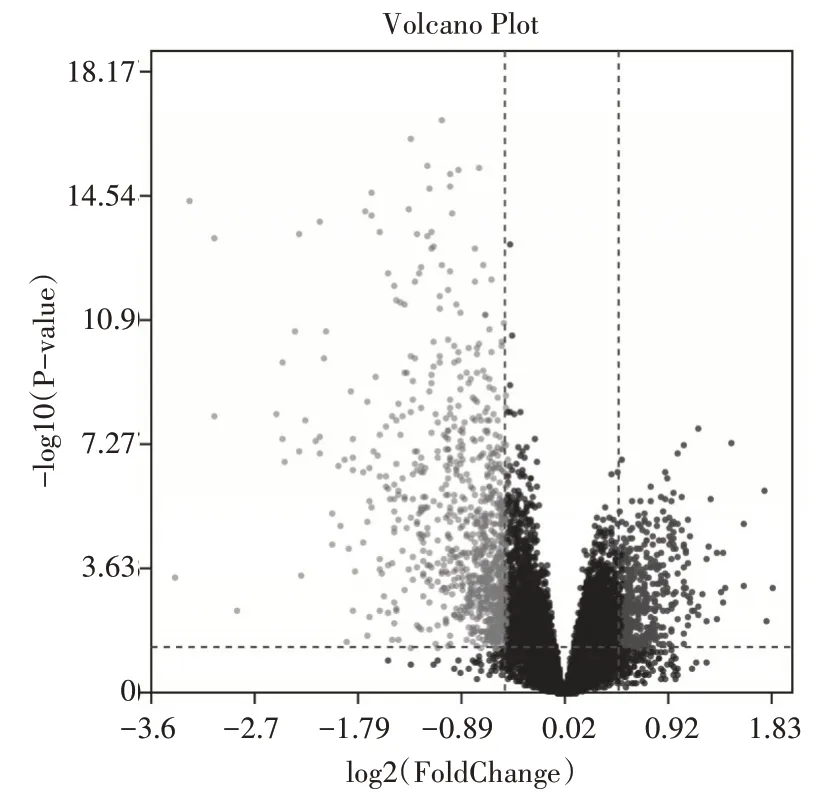
图1 火山图

图1 为火山图，基因差异表达分析的结果。横轴是log2（FC），纵轴是-log10（P value），每个点代表一个基因。

3.2 建立结构方程模型

在结构方程模型中，把外生观测变量基因变量设定为X，ξ即基因潜变量，用来表示基因的综合作用。把Y设定为内生观测变量，η即疾病潜变量，用来表示疾病性状的综合作用。为了确定ξ，对S1组基因进行聚类，如图2所示。然后对不同的聚类结果分别做因子分析验证，同一个聚类下的基因的共同作用用一个潜变量来表示。这个过程是用Mplus软件完成。

图2 热图

为了确定潜变量的数目，使用贝叶斯信息准则（BIC）［9～10］来决定把基因聚为几类，以此确定结构模型的最佳模型。根据表1 列出的结果可以看出，当潜在类别数量逐渐增加时，模型的BIC 值先减小后增大。在8 个模型中，聚类5 的BIC 值最低（25167.205），所以选择聚类5 为最佳模型，即有5个基因潜变量。

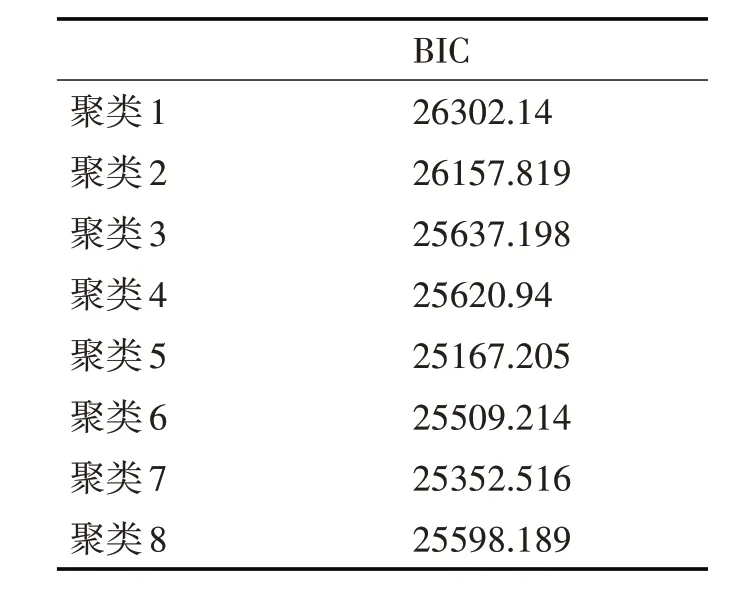
表1 基于不同聚类结果的因子分析结果

图2 为热图，对基因表达量进行标准正态化，然后计算基因表达值之间的欧氏距离进行聚类。

表1 为基于不同聚类结果的因子分析结果，通过模型评估标准确定最佳测量模型。

在确定好ξ和η后，又选取肺癌患者临床指标数据中的3 项作为内生观测变量Y，并且用一个内生潜变量η来表示。建立了基因与疾病相关性状之间的结构方程模型，采用极大似然法进行拟合［11］。对基因组S2和S3利用以上相同的方法建立结构方程模型。通过因子分析验证，选择模型7为S2组基因的最佳模型，选择模型8 为S3 组基因的最佳模型。

在建立的结构方程模型中，疾病潜变量和基因潜变量之间的路径系数代表基因对疾病性状的影响。对3 组路径系数进行了分析比较，如表2。在S1 组中有5 个基因潜变量，最显著的是0.835，这个基因潜变量代表9 个基因的综合作用；S2 组中有7个基因潜变量，最显著的是0.823，涵盖了5 个基因；S3 组中有8 个基因潜变量，最显著的是0.722，代表4个基因的综合作用。

表2 为疾病潜变量和基因潜变量之间的路径系数，从S1 到S3 模型，每组基因不同，所以基因潜变量的数目也不同。

3.3 相关性分析

为了验证得到的基因的综合作用以及和疾病性状的相关性，选出在三组实验中对疾病性状影响最大的基因进行分析。对单一基因和单一性状做了双变量相关性分析，然后对基因总体和性状总体做了典型相关分析。结果如表3 和表4，双变量相关性分析结果表明单个基因和单个性状之间几乎没有相关性，而典型相关分析结果表明基因总体和性状总体是显著相关的。

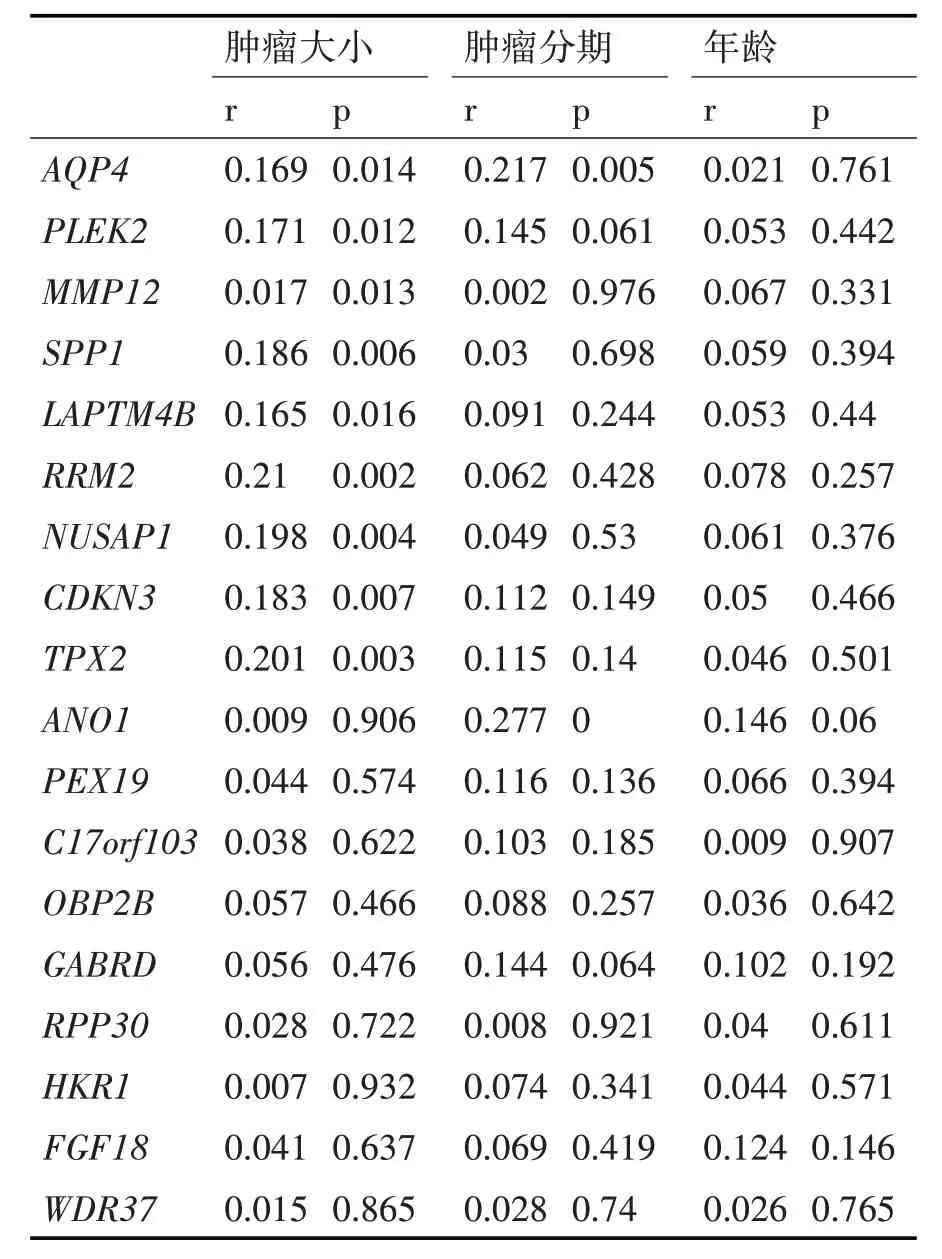
表3 双变量相关性分析结果

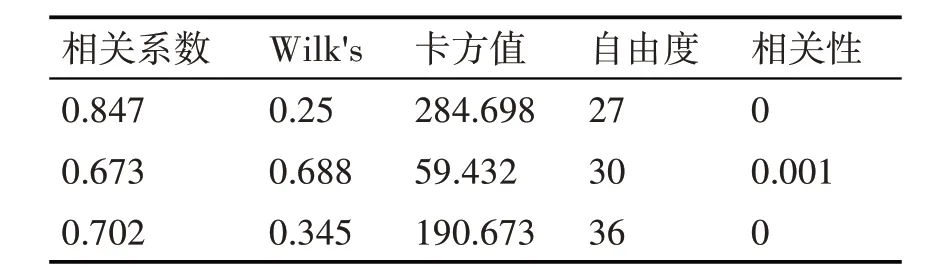
表4 典型相关分析结果

通过相关性分析，不仅可以说明这部分基因是和疾病性状或病人生存有明显的关联关系，更重要的是它们验证了基因的综合作用，证明通过结构方程模型得到的这部分基因是通过基因间的相互作用和疾病性状显著相关的。从而证明通过结构方程模型得到的结论是有显著意义的。

表3 为双变量相关性分析结果。每一个基因和每一个性状分别做双变量相关性分析。是结构方程模型中的疾病性状。

表4 为典型相关分析结果。三组基因分别计算基因整体和所有性状的的相关性。相关性＜0.05证明显著相关。

我们还对得到的基因做了文献挖掘，在我们得到的和疾病性状相关的基因中，很多基因已有资料证明和肺癌或者癌症的发病或治疗是有密切联系的。AQP4 是AOPs 水通道蛋白基因家族成员，AQPs 与癌症生物学功能密切相关，并在二十多种人类癌细胞中都有表达［12］，与肿瘤的类型、等级、增殖、迁移及血管生成均相关［13～14］。MMP12 是一种基质金属蛋白酶，对非小细胞肺癌的局部复发和远处转移具有较好的预测价值［15］。在肺腺癌肿瘤组织中表达水平上调，可能参与肺腺癌发生、发展［16］。SPP1 是一种骨桥蛋白，它的表达同肿瘤的致癌作用和转移密切相关，可能作为肿瘤发生的一个标志物。它在肺癌中高表达，是癌旁组织的6 倍以上，具有极为明显的差异，提示可以用作临床指标用于监测癌肿复发或转移［17～18］。CDKN3 被认为在细胞周期调控中发挥重要作用。研究发现，CDKN3的过表达与卵巢癌、肾癌等多种实体瘤的增殖密切相关［19～20］。

4 结语

我们最后通过结构方程模型获得了三组和疾病性状相关的基因，一共18 个基因。并且通过相关性分析验证他们的综合作用是和疾病显著相关的。复杂疾病的性状是受许多基因控制的，和许多基因都相关，但是单个基因的作用是微弱的，只有它们的综合作用才可以产生共显性的效应。所以在通过结构方程模型得到的基因中，单个基因并不都是和该疾病相关的，但是基因和基因之间是存在相互作用的，他们综合作用的结果是和疾病性状显著相关的，从而证明通过结构方程模型得到的结论是有意义的。

基因数目庞大且基因间的作用复杂难以估计，结构方程模型对于衡量多个基因的综合作用，理清观测变量、潜变量之间的关系无疑是一种很好的方法，然而结构方程模型也有它的局限性。第一，结构方程模型对样本大小有较高的要求，特别是在假设较为复杂的模型的情况下，意味着有更多的未知参数需要估计；第二，由于结构方程模型是一种验证性方法，它对所要研究的变量结构要求有一定的先验信息，以便建模。在本文中，是对基因聚类后建模。在接下来的工作中，也可以针对这一点，利用其它方法，充分挖掘基因数据中的信息，建立更适合衡量基因综合作用的模型。