基于改进支持度的飞行数据记忆融合滤波算法*

颜廷龙 李 瑛 王凤芹

（海军航空大学岸防兵学院 烟台 264001）

1 引言

现有的研究表明，机载参数飞行记录系统采集的飞行数据原值存在噪声干扰、数据缺失等问题［1］。如果不经过数据预处理，难以满足飞行数据二次应用开发的要求。飞行数据预处理是后续如飞行动作识别，飞行状态监控等数据分析工作的基础，而机载参数飞行记录系统采集的飞行数据具有多源性和冗余性的特点，这就为应用多源数据融合技术处理飞行数据提供了信源保证。

目前的飞行数据滤波算法通常是针对单一飞行参数滤波方法，如小波变化［2］、人工神经网络［3］等，这些方法缺乏普适性，如果参数发生改变，需要重新建模。而利用多个传感器针对同一参数的测量值，运用合理的融合滤波算法通常会得到更加可靠的数据。

由于飞机上采集记录飞参数据的设备较多，测量手段丰富，因此飞行数据具有多源性和冗余性的特点，这就为应用多源数据融合技术处理飞行数据提供了信源保证。一方面，军用飞机上常常有多套飞行数据采集装置，如惯导系统，航姿系统等，所以不同的数据记录装置可以为飞机在同一时刻对于同一个参数提供多个数据记录值；另一方面，同一任务记录装置的不同信源针对同一参数的观测值不同，比如惯导系统提供的飞机俯仰角和航姿系统提供的飞机俯仰角，气压计测量的飞机高度和无线电高度等。

目前数据融合算法的分类方法很多，按照是否依赖先验知识可以分为两类：一类是依赖先验知识的数据融合算法，如贝叶斯方法［4］、卡尔曼滤波方法［5～7］等，这些方法的融合效果要依赖于提供的先验知识，但是在实际工程应用中，先验知识的获取往往是困难的；另一类是不依赖于先验知识的方法，如基于支持度一致性的融合算法［8］、基于关系矩阵的融合算法［9］、基于参数之间相互距离的融合算法［10］等。这些算法可以在难以获取先验知识的场合下应用。但是随着数据量的增加，一方面算法的运算效率减慢，另一方面，由于旧数据的增多，递推算法失去修正能力。本文选用基于改进支持度的记忆融合滤波算法对单一飞行参数滤波，既保证了滤波的效果，也能提高算法的运算效率［11］。

2 基于改进支持度的记忆融合滤波算法

2.1 基于斜率距离的支持度

支持度是衡量多源系统中两个信号源在某一时刻之间的相似程度。在由n个信号源观测的某个参数X的多源系统中，其在k时刻第i个信号源的观测值为zi(k) ，根据飞行数据统一误差模型zi(k)=X(k)+V(k)，其中V(k)表示参数第k时刻的所有误差之和，E[V(k)]和D[V(k)]等分布情况均未知。此时可以采用数据融合的方法估计真实数据，即运用支持度来表示数据源观测值的可信程度，给每个数据源分配恰当的权重，进而融合各个数据源的观测值，消除数据的误差，得到飞行参数X真实值的估计值。

数据源的相似程度可以用数据源之间的差异性来衡量，其差异程度采用时间序列的绝对距离计算。在k时刻，数据源i和数据源j的绝对距离为dij(k)，表达式为

为了便于后续运算，统一量纲，对绝对距离dij(k)归一化，记作dij

′(k)，表达式为

运用常用的指数衰减函数来量化两个数据源之间的观测支持度存在两个问题，一是支持度函数含有人为设定的参数，包含一定的主观成分，二是未考虑同一数据源在观测区间采集数据的可信度。为了更可靠地衡量两个数据源之间的支持度，本文提出一种改进支持度函数，引入灰色接近度理论，定义数据源i的自支持度为

式（3）中σi(k)为第i个信号源的观测值zi(k)的方差，所以k时刻数据源i和数据源j的观测支持度为aij(k)，即：

由式（4）可知，如果zi(k)与zj(k)相差较大，则aij(k)较小，数据源i和数据源j之间的相互支持度较低；如果zi(k)与zj(k)相差较小，则aij(k)较大，数据源i和数据源j之间的相互支持度较高。式（5）中，α为支持度系数，反映支持度和数据源相差大小的关系。

应用式（4）可以得到在一定时间段内，参数各个数据源X支持度矩阵为

支持度矩阵每i行元素之和，反映第i个数据源和其他数据源的一致程度，若大，表明第i个数据源和大多数数据源是一致的，反之，则表示与大多数数据源存在偏差。

定义k时刻数据源i观测值与其他数据源观测值的一致性度量为ri(k)，表达式为

根据支持度的定义，通常选择在整个时段观测一致性度量ri(k)较大的数据源作为可靠的数据。但是数据源的观测一致性在不同时刻的变化较大，很有可能出现在某一时刻观测一致性较大，在其他时刻观测一致性较小的情况。所以，仅比较单一时刻的观测一致性无法确定哪个数据源更为准确和可靠，要衡量整个时刻数据源观测一致性的变化规律，本文运用统计理论，通过比较信号源i的观测一致性均值和观测一致性方差，来确定数据融合的权重。

k时刻数据源i观测一致性均值为

k时刻数据源i观测一致性方差为

定义k时刻数据源i的加权系数为qi(k)，在应用过程中，观测一致性均值大，观测一致性方差小的数据源往往被认为更加可靠，所以观测一致性均值大，观测一致性方差小的数据源的权重应该较大，即加权系数qi(k)与数据源i观测一致性均值成正比，与观测一致性方差成反比。因此，加权系数qi(k)的表达式为

其中λ是可调参数，可以调节方差对于权重大小的影响，所以基于支持度的融合估计表达式为

2.2 剔除异常支持度

即使考虑根据数据源的稳定程度，若想获得更为精准的融合结果，还需要在进行数据融合之前，剔除异常支持度对融合结果的影响。本文选用格拉布斯（Grubbs）法剔除支持度中的异常值［12］。

k时刻数据源i的支持度的均值和方差分别为

aij(k)对应的Grubbs统计量为

若Tij(k)≥T(N,a)，则令k时刻数据源i的支持度aij(k)为0。

为了防止数据饱和问题，引入遗忘函数，时间间隔越大的数据，其影响越小；反之，时间间隔越小的数据，其影响越大。由遗忘函数的定义可知，任何单调非增函数都可以是遗忘函数。

2.3 遗忘函数

本文根据指数遗忘函数的特点构造了遗忘函数［13］为

其中t是当前时间差与过去某个时点的时间差，构造的遗忘函数具有形式简单，工程上易于应用的特点。

引入遗忘函数之后，此时的融合估计表达式为

式中wi(k)为记忆融合值的权值，表达式为

3 仿真分析

选取某型飞机发动机转速为试验样本，分别截取飞参系统的主记录器、块卸记录器和事故记录器中关于发动机转速的数据，共400 组，分别记作数据源A，数据源B 和数据源C，真实值为6000r/min，数据源的部分观测数据如表1所示。

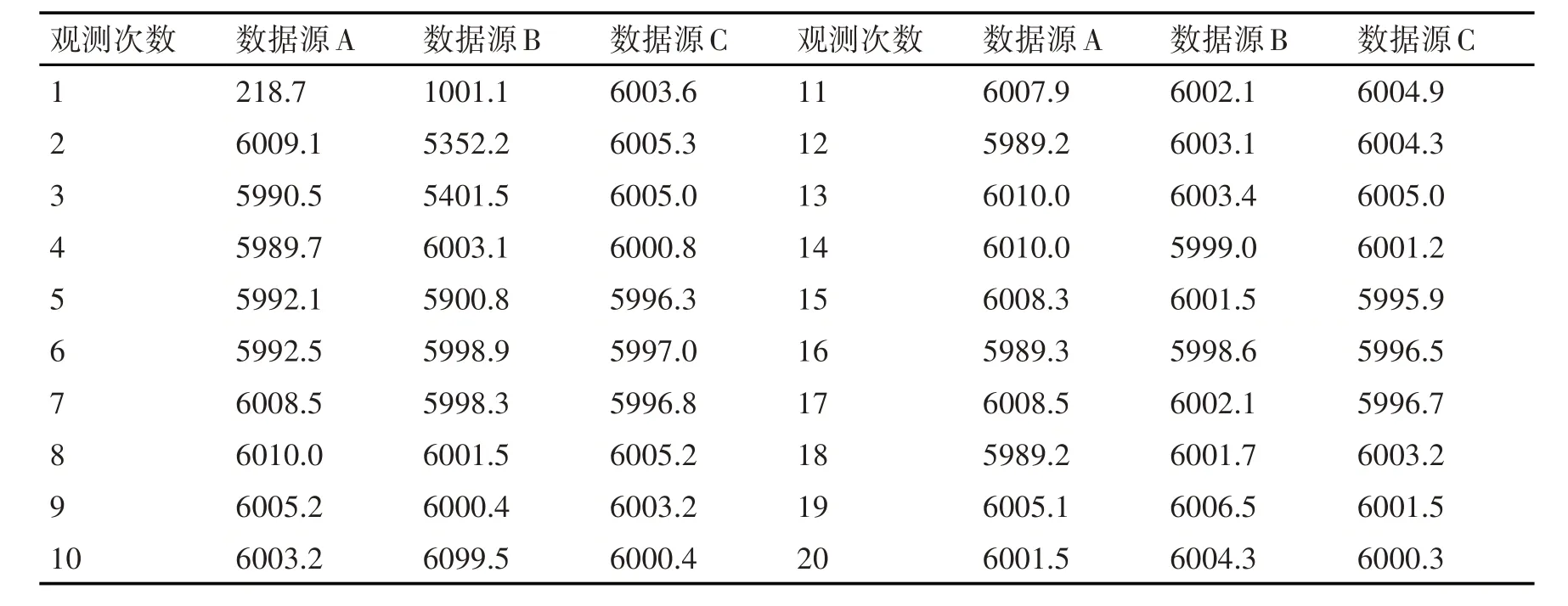
表1 数据源观测数据

采用本算法融合后的数据，与各数据源的原始数据比较如图1 所示，可以看出应用本算法可降低数据源本身存在的噪声，提高了数据源的精度。下面将本算法与其它算法比较，如图2所示。

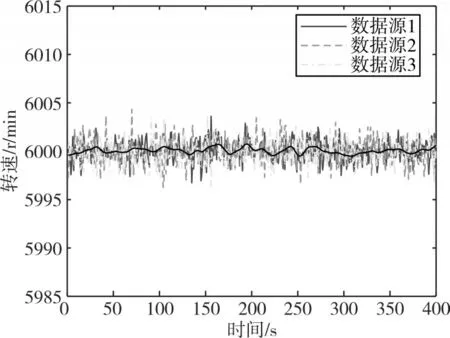
图1 融合结果与数据源输入值比较

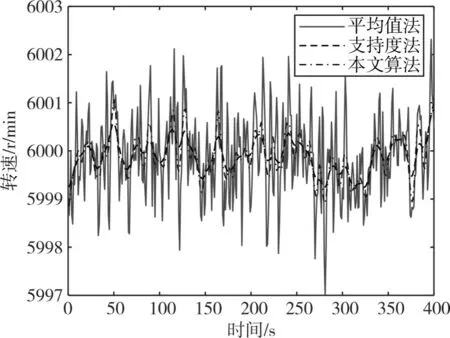
图2 三种算法比较

从图2 可以看出与平均值法和支持度融合算法相比，本算法拥有较好的适应性，滤波结果更接近实际值，数据更加平稳，总体误差小于其他两种方法，极大地提高了飞行数据的精度。

4 结语

对于机载参数飞行记录系统采集的飞行数据原值存在噪声干扰问题，本文根据飞行数据具有多源性和冗余性的特点，提出在已有的支持度算法上的改进支持度记忆融合滤波算法，通过对改进的支持度计算和添加遗忘因子，使得算法的效率增加，提高了数据的精度。