自由液面对NACA0012 翼型流体动力特性影响研究

刘 钊,黄 闯,杨 昊,贺 旭,党建军

(西北工业大学 航海学院,陕西 西安,710072)

0 引言

水下航行器具备良好的隐蔽性,在海战中具有突防能力强的特点。但由于水介质密度大,水下航行器在行驶中所受阻力很大,航速和航程有限[1]。跨介质航行技术不仅可充分发挥水下航行器隐蔽性好的优势,还能有效弥补其在航程和航速上的不足,受到广泛关注。在空中航行阶段,为了平衡重力,跨介质航行器需要配置机翼产生足够的升力。然而,机翼的流体动力特性在接近自由液面过程中会受到显著影响,表现出与远场不同的特性[2]。因此,掌握机翼近自由液面的流体动力特性,对跨介质航行器的总体设计和航行控制至关重要。

关于跨介质航行器,国外学者已经开展了一些研究工作。Weisler 等[3]验证了固定翼跨域无人航行器在跨越自由液面时可以保持良好的操控性。Siddall 等[4]通过风洞和水洞实验发现变形水上微型飞行器可以实现被动俯冲入水。以上研究证明,跨介质航行器在工程上具有可实现性。机翼是跨介质航行器的关键部件,其在接近自由液面时的工作特性也受到了关注。王岱峰等[5]发现NACA0012 翼型在近水面随高度降低出现前压力驻点,且高压区域向后缘扩展。喻海川等[6]对小展弦比NACA4415 机翼开展地效区数值仿真,发现当高度达到一倍弦长时,机翼流体动力特性出现明显变化。Marshall 等[7]通过风洞实验验证不同边界层厚度对机翼地面效应的影响,指出边界层厚度增加会导致机翼下表面压力增大。屈秋林等[8]采用数值仿真方法对某地效飞行器在近地面巡航的气动性能进行研究,指出飞行高度的降低会导致飞行器升力、阻力和升阻比的增加。

与机翼从空中接近自由液面的相关研究不同的是,水下近自由液面流体动力特性研究主要集中在航行器阻力方面。Nematollahi 等[9]采用计算流体动力学(computational fluid dynamics,CFD)方法研究水下航行器与自由液面的相互作用,发现自由液面附近水下航行器的阻力主要有粘性阻力和兴波阻力,且随深度减小阻力系数增大。姜宜辰等[10]采用数值仿真方法研究了艇体形状对阻力的综合影响,得出压差阻力变化是导致艇体总阻力变化的主要原因。何广华等[11]建立求解水下潜体兴波阻力的数值模型对潜艇近水面航行的兴波阻力特征进行仿真,得到随着航深的增加潜艇兴波阻力系数逐渐减小。对比上述研究发现,自由液面对空中和水下航行体的影响机理并不相同。

根据国内外公开发表的文献,关于机翼在半无限流场中的流体动力特性研究多集中在空中近水面或近地面情况,机翼从空中和水下远场逐渐接近自由液面过程的流体动力特性研究鲜见。此外,机翼在水下近自由液面的流体动力特性研究还相对缺乏,相关研究多集中在类回转体外形的阻力特性方面。因此,文中针对机翼从空中和水下分别接近自由液面的过程建立数值仿真模型,研究机翼在接近自由液面过程中的流体动力特性变化规律,分析机翼近自由液面流体动力特性的变化机理。研究从模型建立、数值仿真结果、分析与讨论3 个方面展开,为工作在自由液面附近的带翼航行器总体设计提供参考。

1 模型建立

1.1 数值仿真模型

为研究机翼在近自由液面的流体动力特性,需采用多相流模型建立包含自由液面的特殊两相流场。相较于Mixture 模型多用于离散项分布较广的情况,流体体积(volume of fluid,VOF)模型主要用于跟踪几种不相容流体的交界面位置及其运动规律[12]。由于研究涉及气液两相流动和自由液面仿真,为建立机翼从远场接近自由液面的两相流场,采用VOF 多相流模型仿真气相、液相及气液交界面。

所研究机翼的航行速度很小,流场密度几乎不变,可压缩性忽略不计。将空气和水当作不可压缩介质处理,且不涉及换热问题,可不考虑能量方程,按常温处理,假设流场温度15℃,仅以连续性方程和动量方程作为多相流场的基本控制方程。

对于多相流中的第q相来说,其连续性方程具有如下形式

式中: αq为第q相体积分数;v为速度矢量;ρq为第q相密度。

为了满足方程的可解条件,各相体积分数还应满足

式中,n为总相数,这里取n=2。

匀质平衡流模型中各相间不存在速度差,基于平均密度和平均动力黏度的流体微元动量方程为

式中:f为流体微元受到的体积力;ρm、µm分别为流体微元的各相平均密度和各相平均动力黏度,且

由于气相和液相的雷诺数差异较大,为准确描述机翼上表面逆压梯度和多相流场内压力分布,需选择合适的湍流模型。Realizablek-ε湍流模型能够更精确地预测强逆压梯度边界层流动,稳定性良好,适合用于求解机翼从远场接近自由液面的两相流场[13-14]。Realizablek-ε湍流模型的湍动能及湍流耗散率输运方程如下

式中:k为湍动能;µ为动力粘度;µt为湍流粘性系数;k1为平均速度梯度产生的湍动能,k2为浮力产生的湍动能;ε为湍流耗散率;YM为湍流脉动膨胀对总湍流耗散率的影响;η=S k/ε,S为平均应变率;C2=1.9为常数;C1ε=1.45为常数;C3ε为浮力影响湍流耗散率的函数;σk=1.0,为湍动能的湍流普朗特数;σε=1.3,为湍流耗散率的湍流普朗特数。

采用商业CFD 软件STAR-CCM+对机翼距自由液面不同距离的流体动力特性进行仿真计算。压力速度耦合采用Simple 算法,结合Rhie-Chow插值进行压力修正,对流项为2 阶迎风格式。

1.2 计算域及边界条件

选用NACA0012 翼型作为研究对象,机翼弦长为100 mm,展弦比为10。建立数值计算模型,对机翼固定高度的稳态流体动力特性进行研究,通过改变机翼形心与自由液面的距离h,研究机翼接近自由液面时的流体动力特性变化规律。

计算域入口采用速度入口,空中工况速度为80 m/s,水下工况速度为20 m/s;计算域出口采用压力出口,出口静压设置为静水压;远场边界采用滑移壁面条件;机翼表面采用无滑移壁面边界条件。应用VOF 多相流模型仿真自由液面位置,仿真工况中机翼采用6°攻角,其与自由液面的距离h以弦长D为参考值确定,归一化高度参数h/D在0.3～90 的范围取值。建立80D×200D×40D的计算域,机翼形心到计算域入口距离为30D。模型计算流域边界示意如图1 所示。

图1 计算域边界示意图Fig.1 Schematic of computational boundary

使用切割体网格加棱柱层控制的网格划分方式,为绕流场划分切割体网格,对机翼附近的边界层建立棱柱层加密。通过建立相应的面控制和体控制策略,在机翼表面划分细致的面网格并捕捉其几何特征;在机翼前缘、后缘和四周建立体积控制区域进行网格加密,棱柱层厚度1 mm,总层数14 层。网格划分细节如图2 所示。

图2 网格划分细节Fig.2 Details of grid distribution

1.3 网格及计算域无关性验证

为了获得网格无关的计算结果,在网格分布规律不变的前提下,改变网格基础尺寸,分别生成网格单元数分别为330 万、630 万和860 万的计算域划分结果并开展仿真计算,其结果对比如图3 所示。

图3 网格无关性验证对比图Fig.3 Result of grid independent verification

由图3 可知,网格单元数从330 万～630 万,阻力系数减小了13.101%,升力系数增大了1.801%;网格单元数从630 万～860 万,阻力系数减小了2.599%,升力系数减小了0.015%。结果表明,网格数量为630 万的计算域划分方案能够满足网格无关性要求。

文中采用有限的计算域仿真机翼在远场中的工作特性,合理的计算域尺寸能够在获得准确计算结果的同时节省计算资源。为了获得计算域无关的计算结果,建立50D×125D×30D(较小)、80D×200D×40D(适中)和100D×250D×50D(较大)3 种尺寸的计算域,确保核心区网格分布规律不变,采用上述确定的网格尺寸划分网格开展仿真计算。3 个算例的结果对比如图4 所示。

图4 计算域无关性验证对比图Fig.4 Result of computational field independent verification

由图4 可知,计算域从较小到适中,阻力系数增大了16.517%,升力系数减小了3.979%;计算域从适中到较大,阻力系数减小了0.306%,升力系数减小了0.155%。结果表明,80D×200D×40D的计算域尺寸能够满足无关性要求。

1.4 模型验证

参考Olayemi 等[15]给出的NACA0012 翼型在不同湍流模型条件的流体动力参数随攻角变化的规律,选择1 m 弦长的NACA0012 翼型,空气密度取1.225 kg/m3,黏度取1.789 4×10-5Pa·s,温度取288.16 K,马赫数为0.13,压力为101 325 Pa,攻角取2°、4°、6°和8°。采用已构建的数值仿真方法对相同工况进行数值仿真,得到机翼的流体动力参数并与实验结果进行对比,如图5 所示。

图5 流体动力系数仿真与实验结果对比Fig.5 Comparison of hydrodynamic coefficient between simulation and experiment

图中,数值仿真得到的NACA0012 翼型流体动力特性与实验结果吻合,阻力系数、升力系数与实验结果的最大相对偏差分别为2.67%和4.46%,表明数值仿真结果具有较高的计算精度。

2 仿真结果

2.1 空中近自由液面流体动力特性

从空中远场逐渐接近自由液面时,机翼的流体动力特性变化如图6 所示。

图6 机翼在空中工况的流体动力特性曲线Fig.6 Hydrodynamic characteristics curves of airfoil under air condition

机翼距自由液面高度从90D减小到0.3D过程中阻力系数的变化主要有4 个阶段: 当机翼工作高度大于50D时,阻力系数随距离增加无显著增大;当机翼工作高度从50D下降到10D时,阻力系数缓慢减小;当机翼工作高度从10D下降到0.4D时,阻力系数迅速减小至0.4D高度,达到最小值;当机翼工作高度小于0.4D时,阻力系数再次增大,此时机翼距离自由液面非常近,其下表面压力显著增加。

对于升力系数,当机翼工作高度大于3D时,升力系数总体变化较小,仅在10D高度处由于下表面压力增大出现极大值;当工作高度小于3D时,由于自由液面阻滞效应,机翼下洗减弱,升力系数出现了迅速上升。

对于升阻比,当机翼工作高度大于50D时,升阻比基本不变;当高度从50D下降到5D时,阻力下降明显,机翼升阻比出现缓慢上升;当机翼距自由液面高度小于2D时,自由液面影响明显,升阻比出现迅速上升。

2.2 水下近自由液面流体动力特性

从水下远场逐渐接近自由液面时,机翼的流体动力特性变化如图7 所示。

图7 机翼在水下工况的流体动力特性曲线Fig.7 Hydrodynamic characteristics curves of airfoil under water condition

机翼工作深度从90D减小到0.3D的过程中,其阻力系数变化可以分为3 个阶段: 当工作深度大于50D时,其阻力系数随距离增加无显著变化;工作深度从50D减小到10D的过程中,由于兴波作用,其阻力系数持续增加,在距离为10D处达到最大值;当工作深度由10D减小到0.3D时,由于自由液面作用,机翼阻力系数迅速减小。

机翼升力系数随工作深度的变化在水下表现出单一性的特征: 当工作深度大于10D时,不同深度机翼的升力系数变化并不显著;工作深度从10D减小到0.3D过程中,受到自由液面作用,升力系数迅速减小。

关于机翼在水下的升阻比变化,当工作在距离自由液面较远的深度时,升阻比呈现出逐渐减小的特征;当工作深度从10D减小到2.5D时,由于阻力系数迅速下降,升阻比出现小幅增加,到深度为2.5D时达到极大值;当工作深度从2.5D减小到0.3D时,自由液面和大气压作用使得机翼上表面的负压程度受限,升阻比迅速减小。

3 分析与讨论

3.1 空中工况计算结果分析

由图6 可知,随着机翼距自由液面距离小于50D,阻力系数缓慢下降。此时翼型距离自由液面较近,自由液面对流场的影响使得机翼的下洗效应减弱,流经机翼后缘的气流速度减小,机翼尾部压力恢复增强,最终导致压差阻力减小。

机翼工作高度从10D下降到0.4D的过程中阻力系数迅速减小,为了分析其原因,分别提取机翼摩擦阻力系数和压差阻力系数的变化规律,如图8 所示。可知,该过程中摩擦阻力系数的显著降低是阻力系数迅速下降的主要原因,随着高度下降,机翼与自由液面之间的通道迅速减小,使得机翼下表面的流速增大,局部雷诺数增大,进而摩擦阻力系数减小。进一步,提取机翼在不同工作高度时前缘和后缘对应的压力系数如图9 所示。机翼前缘的静压随高度降低无显著变化,而后缘的静压随高度降低显著增加,使得机翼前后缘的压差不断减小,因此压差阻力系数下降。机翼工作高度从10D降低至1D过程中,压差阻力系数和摩擦阻力系数都在减小,因此总阻力系数降低。

图8 不同工作高度的阻力系数压差分量和摩擦分量对比曲线Fig.8 Comparison of pressure and fractional components of drag cofficients in different operational altitudes

图9 机翼表面压力系数变化规律Fig.9 Surface pressure coefficient verification law of airfoil

当工作高度小于1D时,压差阻力系数的变化趋势改变,随工作高度的减小而迅速增大。提取高度小于1D时机翼的表面压力系数如图10 所示,随着高度下降机翼低压面压力系数无明显变化,而高压面压力系数显著增加,从而使得机翼上下表面压差增大,造成压差阻力系数明显升高。压差阻力系数和摩擦阻力系数随机翼工作高度的变化表现出不同的规律,二者综合作用使得机翼阻力系数在工作高度大于0.4D时随着工作高度的减小而减小,在工作高度小于0.4D时随着工作高度的减小而增大。

图10 不同工作高度的机翼表面压力系数对比曲线Fig.10 Comparison of surface pressure coefficient of airfoil in different operational altitudes

对于升力系数的变化,当机翼工作高度大于10D时,升力系数随高度下降无显著变化。在工作高度从10D下降到3D过程中,机翼上下表面的压差变化如图9 实线所示,可见随着高度降低机翼上下表面压力差减小,升力系数在这一阶段出现下降。提取机翼表面压力系数如图10 所示,当工作高度小于3D时,由于自由液面阻滞,机翼下表面静压升高,导致升力系数增大。

由上述分析可知,当机翼工作高度大于50D时,机翼未受到自由液面的影响,升阻比无明显变化。当工作高度从50D下降到3D时,机翼附近流速降低,摩擦阻力系数降低导致总阻力系数下降,升阻比缓慢增大。当机翼距自由液面距离小于3D时,受到自由液面的阻滞,机翼下表面压力显著上升,升阻比值迅速增大。

3.2 水下工况计算结果分析

由图7 可知,当机翼工作深度大于50D时,阻力系数随深度减小无显著变化。随着深度减小,机翼运动在自由液面产生兴波,在深度从50D上升到10D过程中,机翼与自由液面距离不断缩小,兴波阻力持续增加,机翼阻力系数不断增大。当工作深度小于10D时,机翼接近自由液面过程中压差阻力系数和摩擦阻力系数的变化如图11 所示。

图11 不同工作深度的阻力系数压差分量和摩擦分量对比曲线Fig.11 Comparison of pressure and fractional components of drag cofficients in different operational depths

机翼的摩擦阻力系数随工作深度减小无显著变化,导致阻力系数下降的主要原因是压差阻力系数的迅速减小。提取深度2.5D～0.3D时机翼表面的压力系数对比如图12 所示,可知随着机翼工作深度减小,机翼高压面压力无显著变化,而低压面因受到自由液面及大气压的影响负压程度减弱,使得上下表面的压力差持续减小,因此机翼的压差阻力系数在自由液面附近随工作深度的减小迅速下降。

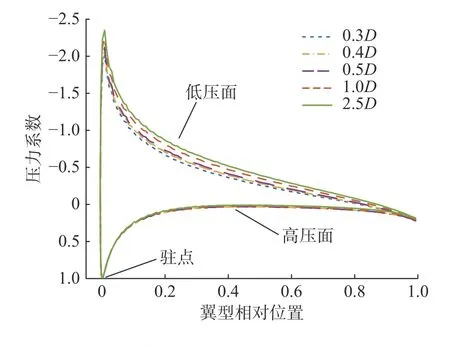
图12 不同工作深度的机翼表面压力系数对比曲线Fig.12 Comparison of surface pressure coefficient of airfoil in different operational depth

当水下工作深度超过2.5D时,机翼升力系数在不同工作深度无显著变化;当工作深度小于2.5D时,升力系数随工作深度的减小迅速降低。对比机翼工作深度10D和0.3D时翼型附近的静压分布如图13 所示,可见机翼接近自由液面时的兴波明显,其上表面的负压程度随工作深度减小逐渐减弱。提取机翼工作在水下不同深度时高压面和低压面的压力系数分布并进行对比,如图12 所示。因受到自由液面和大气压的影响,低压面的负压程度受到限制,使得机翼表面的压差减小,最终导致机翼的升力系数随着工作深度的减小而降低。

图13 翼型附近静压分布对比Fig.13 Comparison of static pressure distribution around airfoil

由上述分析可知,当工作深度大于80D时,机翼的升阻比值随深度减小无显著变化。在工作深度从80D减小到10D过程中,由于兴波作用导致阻力系数上升,升阻比值持续减小。在工作深度从10D减小到2.5D的过程中,压差阻力系数下降导致阻力系数小幅下降,升阻比增大。随着工作深度从2.5D减小到0.3D,机翼上表面的压力降低受到自由液面和大气压的影响,机翼上下表面压差减小,升阻比值迅速降低。

3.3 流体动力特性对比与分析

通过上述分析发现,机翼在从空中和水下远场接近自由液面的过程表现出截然不同的流体动力特性。空中工况中,随着机翼距离自由液面越来越近,机翼的阻力系数下降,升力系数上升,升阻比增大;水下工况中,随着机翼距离自由液面越来越近,升力系数下降,升阻比减小,阻力系数受到兴波和自由液面双重影响先增大后减小。究其原因,自由液面对接近的机翼表现出明显的阻滞作用,机翼距自由液面较近的面压力随距离减小持续增加,造成空中和水下机翼表面压力差的相反变化,直接导致升力系数的相反变化。

此外,机翼在空中和水下两工况的远场升阻比并不相同,水下远场的升阻比明显大于空中远场的值。由于航行速度、介质密度和介质粘度都不相同,使得空中工况和水下工况的雷诺数差异较大,进而导致机翼阻力系数及升阻比特性不同。空中工况雷诺数为5.7×105,水下工况雷诺数为2×106。进一步,采用文中所建模型,在相同雷诺数下开展机翼在空中和水下远场中的工作特性仿真分析,其在阻力系数、升力系数和升阻比的相对偏差分别为0.19%、0.64%和0.45%。

4 结论

文中探究了机翼从远场接近自由液面过程的流体动力特性变化,建立了机翼在不同高度和深度条件的数值仿真模型,验证了模型的可行性,得到机翼逐渐接近自由液面过程的流体动力特性变化。主要结论如下:

1) 从空中远场接近自由液面过程,机翼阻力系数逐渐减小而后小幅上升,升力系数基本不变而后迅速增大,升阻比值随高度降低持续增加。相对于远场工况,当机翼工作高度在0.3D时,阻力系数减小了7.71%,升力系数增大了14.97%。

2) 从水下远场接近自由液面过程,机翼阻力系数先小幅上升而后迅速减小,升力系数基本不变而后迅速减小,升阻比值随深度减小总体呈下降趋势。相对于远场,当机翼工作深度在0.3D时,阻力系数减小了14.84%,升力系数增大了21.45%。

3) 当机翼在空中距离自由液面0.3D～0.4D时,因下表面的静压升高明显,导致阻力系数随距离的减小略微增大。机翼在水下距离自由液面超过10D时,阻力系数变化主要受到兴波作用的影响,距离小于10D时则主要受到大气压力的影响。

文中未尽之处在于仅采用准稳态方法研究了不同距离下自由液面对NACA0012 翼型流体动力参数的影响,之后将结合跨介质航行器研究机翼接近和远离自由液面的非定常流体动力特性,为跨介质航行器的设计与控制提供参考。