某动力涡轮转子连接圆弧端齿的优化设计

徐鲁兵，廖明夫，吕延军

（1.西北工业大学 动力与能源学院，西安 710072；2.中国航发湖南动力机械研究所，湖南株洲 412002；3.西安理工大学 机械与精密仪器工程学院，西安 710048）

圆弧端齿（Curvic couplings）是端齿盘的一种特殊结构形式，具有结构紧凑、定心精度高、承载能力强、连接稳定性好的优点，现在已成为了一种典型的可靠性较高的转子连接结构，被广泛应用于不同种类的高速转子和重载机械设备的传动装置中[1]。同时，圆弧端齿所特有的装拆方便性、互换性,使得重复加载和多次拆装也不影响其原有的定心精度，在航空发动机转子部件的连接中也被大量应用，特别是基于航空发动机结构设计中的“单元体”设计理念，圆弧端齿结构作为一种典型的转子连接结构，使得单元体设计的优势更加突出,如RTM322、MTR390、T700、T800 等涡轴发动机及Trent 系列、EJ200、RB199 和RB211 等航空涡扇发动机[2-4]均采用圆弧端齿连接结构实现了单元体设计，在保证转子定心可靠、连接稳定的基础上，大大提高了发动机的装配性、互换性和外场维护性。

国内外学者在圆弧端齿（端面弧齿）的强度及接触分析、连接刚度及动力学、端齿结构设计及优化等方面已进行了不少研究。李业明等[5-6]研究了大功率机车用圆弧端齿应力分布规律和参数优化。袁淑霞等[7-9]建立了带有周向拉杆螺栓的重型燃气轮机转子失谐刚度模型，研究了拉杆失谐对转子动力学特性及端面弧齿应力分布的影响，其中考虑了拉杆螺栓和螺栓孔侧壁的动态接触以及摩擦力和接触等非线性因素的影响。在端齿强度及接触分析方面，Richardson 等[10-11]进行了圆弧端齿结构的三维有限元接触分析，并对圆弧端齿等效模型进行了光弹测试实验，计算分析的齿根处应力分布趋势与光弹测试结果吻合较好。Jiang 等[12]基于接触力学和摩擦磨损理论研究了一对端齿的接触应力分布，提出将平面的齿面改为弧形凸起齿面可在一定程度上改善齿面应力分布。李浦等[13]采用平面冲压模型对重型燃气轮机轮盘端面齿进行了三维端齿接触应力分析，初步验证了平面冲压模型的正确性。沈洋与曹鹏[14]针对涡轴发动机压气机连接端齿进行了不同设计参数对端齿接触状态的影响分析，认为转速是引起端齿连接结构接触状态变化的主要原因，而轴向压紧力直接影响接触应力和滑移距离，这会加剧齿面的接触损伤。另外，圆弧端齿也会对转子连接的刚度产生弱化作用，进而影响转子动力特性。Yu 等[15]研究指出由于接触角和表面粗糙度的影响，圆弧端齿的确会减小连接刚度，且粗糙表面对刚度损失的影响最大。Liu 等[16-17]研究了不同载荷条件下圆弧端齿对连接刚度的弱化影响，表明压力角是引起端齿刚度弱化的主因，且对压缩刚度和弯曲刚度的影响更敏感。文献[18-19]在获得端齿连接刚度时考虑了齿面粗糙度的影响，提出了可表征接触效应影响的端齿连接结构刚度等效方法，进而研究了不同预紧力作用下的转子动力学特性规律。而在圆弧端齿结构设计及优化方面，业界学者主要是针对细节结构进行应力优化以提高端齿疲劳寿命，Muju 和Sandoval[20]申请了一项美国专利，提出了圆弧端齿根部的双段圆弧复合倒圆结构以减小齿根应力和提高疲劳寿命。Pisani 和Rencis[21]采用二维、三维有限元分析方法得到了压气机部件圆弧端齿的应力集中系数，仅针对一个齿在离心力下的受力情况进行分析，未对端齿进行接触分析和优化设计。黄发和李爱民[22-25]等针对航空发动机压气机转子提出了圆弧端齿结构设计方法，采用神经网络-遗传算法对圆弧端齿齿根双圆弧结构进行了优化设计，减小了齿根应力，改善了齿根应力分布，并进行了端齿微动疲劳寿命预测及模拟件寿命试验研究。

在航空发动机的实际工程应用中，圆弧端齿用于转子连接通常有两种方式：圆弧端齿+单个拉杆、圆弧端齿+多个拉紧螺栓。相比其他的如法兰止口+螺栓的转子连接方式，圆弧端齿连接不必设计像止口那样的过盈配合，而且装配分解时不需要对零件过盈部位进行加热或冷却，也无需专用的装配、拔卸工装，更有利于实现单元体设计和外场更换维护。然而，当采用多个拉紧螺栓对圆弧端齿施加预紧力时，螺栓孔必然会破坏圆弧端齿齿形结构的完整性，使得接触区域受力情况变得更加复杂，其强度和寿命安全裕度有所降低。

国内外学者主要关注于完整齿形结构圆弧端齿的强度、接触特性和连接刚度等方面研究，而对螺栓孔破坏端齿结构完整性这一问题研究的较少。本文以某涡轴发动机动力涡轮转子盘轴连接采用的拉紧螺栓预紧的圆弧端齿连接结构为研究对象，建立参数化模型，对其进行有限元静强度分析，并研究了螺栓孔径向位置以及外径等参数变化对圆弧端齿结构应力的影响，确定了设计变量的取值范围，以外径和齿宽两个关键参数为设计变量，对圆弧端齿进行了结构强度优化设计，并分析了优化前后各个应力参数的变化情况。

1 模型建立

1.1 计算模型

本文研究的某动力涡轮转子盘轴连接及圆弧端齿的几何模型如图1 所示，载荷及部分结构参数见表1。模型中将叶片的离心载荷等效施加到涡轮盘轮缘上。转子采用周期对称性模型；为了模拟螺栓预紧力，建立等效螺栓部件（图2），通过预紧力单元实现预紧力加载。

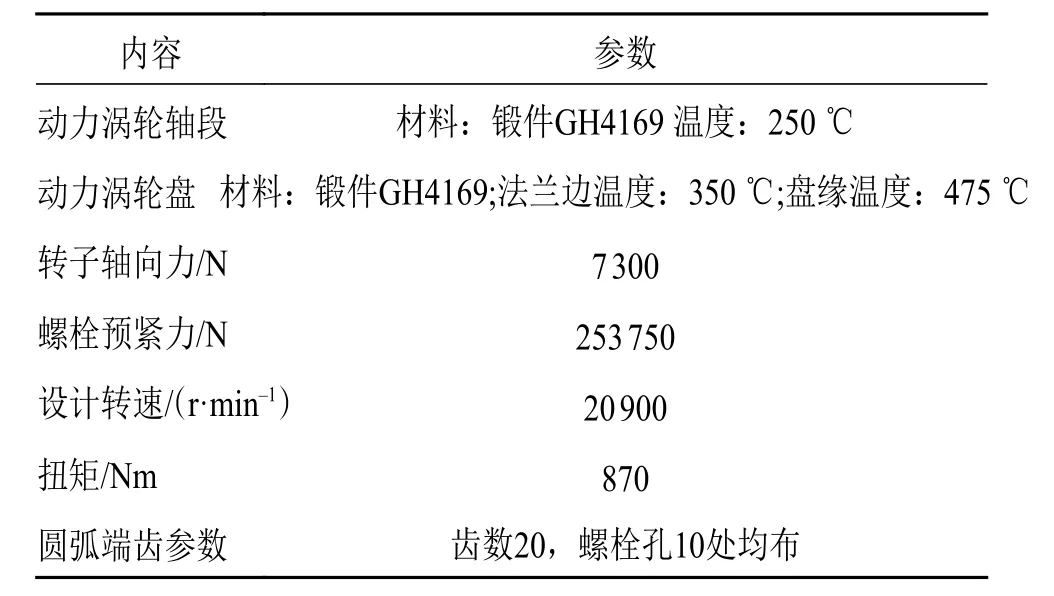
表1 动力涡轮转子设计参数

图1 动力涡轮转子及轴端圆弧端齿的三维模型

图2 动力涡轮转子及轴端圆弧端齿的有限元模型

以有限元分析软件ANSYS 软件为平台，采用三维接触分析方法，对凹齿和凸齿在装配工作状态下的受力情况进行分析。有限元网格采用三维高阶20 节点6 面体实体单元Solid186 进行划分，此单元适用性强，对于复杂构件的网格离散，可以退化为四面体单元。对于圆弧端齿结构，为了在端齿部分得到较为精确的结果，对端齿部分采用较为精细的网格，对轮盘部分采用较为稀疏的六面体扫略网格，有限元网格如图2a）所示。同时，为了保证端齿接触面的计算精度和可靠性，对端齿接触面区域进行网格局部加密，如图2b）所示，对接触面采用contact174 和target170 单元建立接触对，模拟装配之后端齿的工作状态。最终划分单元120388 个，节点189787 个。

1.2 边界条件设置

对1/10 模型的扇形边界施加循环对称约束，保证扇形边界高低面的位移协调；对转子轴段上的轴承配合面施加轴向、周向和径向约束，模拟轴承约束；凹齿与凸齿通过施加接触对保证连接，其中接触对使用标准摩擦接触，接触摩擦因数设置为0.2，采用增广拉格朗日接触算法求解；螺栓与轮盘、螺栓与轴的连接通过创建绑定接触实现，模拟螺栓施加预紧力之后始终与轴和轮盘紧密连接并传递轴向力；采用预紧力单元法施加螺栓预紧力，对等效螺栓建立预紧力单元（prets179 单元）；建立主节点，与转子右侧轮毂的右端面进行节点自由度耦合，气动轴向力和扭矩均施加在耦合主节点上；离心载荷以转速的形式施加，温度载荷按均温考虑。

2 优化设计方法

2.1 优化问题描述

本文从圆弧端齿结构设计的角度，选取外径D0和齿宽B两个参数为优化设计变量，以全局最大等效应力值为优化目标，以最大径向应力、最大周向应力、接触面平均挤压应力、接触面平均剪切应力为应力约束条件，采用ANSYS 优化模块的零阶方法的子问题法进行全局寻优。优化计算时设计变量、状态变量和目标函数容限的选择策略为：遵循先选较大的容限确定最优解的范围，再选较小的容限获得精确值，既可以保证寻优的精度，又可以避免陷入局部最优点。

结合圆弧端齿设计文献[1]中的准则和斯贝MK202 发动机应力标准[26]，得到本文优化问题的约束条件为：1）圆弧端齿结构的最大径向应力不超过屈服极限σ0.2的75%；2）圆弧端齿结构的最大周向应力不超过屈服极限σ0.2的95%；3）圆弧端齿接触面平均挤压应力不超过极限强度 σb的25%；4）圆弧端齿接触面平均剪切应力不超过极限强度 σb的20%；

根据工程常用的5%的设计变量取值范围，确定外径D0的变化范围在93～ 103 mm 之间；圆弧端齿的齿宽B不能设计的过小或过大，过小的齿宽会导致接触面过小而承载能力变弱，而齿宽过大会引起齿面磨削加工时在内径齿根过渡处过切削或外径处欠切削。所以综合考虑本文研究对象的结构几何尺寸和加工工艺性，确定的齿宽B的变化范围在15～18 mm 之间。

由以上分析，可以得到圆弧端齿结构优化的数学模型为

式中：σeqv,max为最大等效应力；外径D0和齿宽B为设计变量；状态变量 σj为应力约束条件的4 个应力分量，即σrmax为最大径向应力，σθmax为最大周向应力，σcont,avg为接触面平均挤压应力，στ,avg为接触面平均剪切应力；为对应的许用应力值。

2.2 优化结果与分析

求解分为多载荷步加载，其中第一步施加所有边界条件，而载荷仅施加螺栓轴向预紧力，模拟圆弧端齿在非工作状态下的静止装配状态，第二步在第一步的轴向预紧力的基础上，将转速、扭矩、气动轴向力和温度载荷全部施加，模拟圆弧端齿工作状态下的受力状态。

以最大等效应力为优化目标，优化前、后圆弧端齿的齿形参数见表2，优化目标和设计变量、状态变量的优化迭代过程见图3～ 图6。

表2 优化前、后的圆弧端齿齿形参数

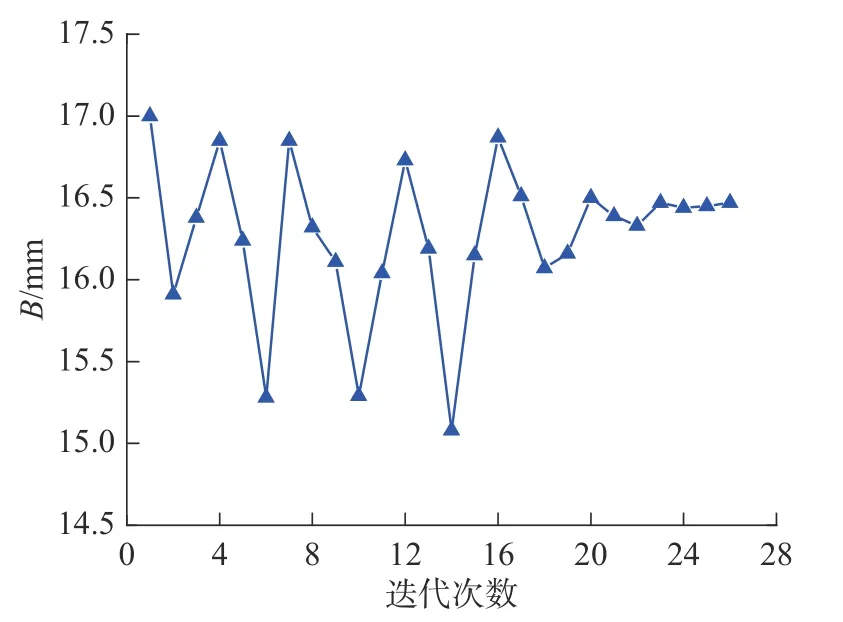
图3 设计变量齿宽B 值的优化迭代过程

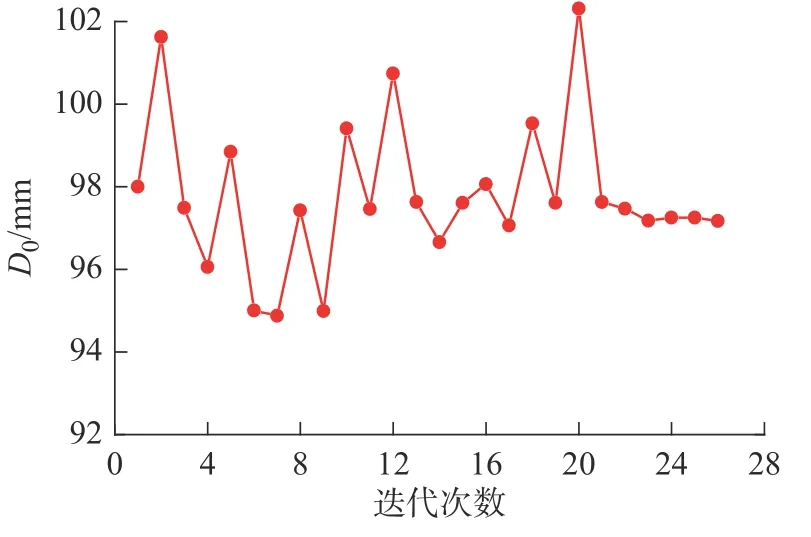
图4 设计变量外径D0 的优化迭代过程

图5 优化目标的收敛情况

图6 归一化状态变量的优化迭代过程

由图3～ 图6 优化迭代过程曲线可知，最大等效应力经过15 次左右迭代就逐渐收敛于最小值，外径D0基本收敛于97.18 mm，而齿宽B基本收敛于16.47 mm。图6 中的归一化状态变量，为4 个状态变量与其许用应力的比值关系，由图可知，最大径向应力、最大周向应力、接触面平均挤压应力、平均剪切应力四个归一化状态变量均落在0～ 1 之间，说明这4 个参数在优化迭代过程中，均能很好满足约束条件的要求。

优化前、后的有限元分析的应力结果见表3，应力分布图如图7 与 图8 所示。

表3 优化前、后的圆弧端齿有限元应力结果

图7 动力涡轮转子的变形分布图

图8 动力涡轮转子的全局等效应力分布图

从图7 可以看出，动力涡轮转子的全局变形量发生于轮盘轮缘，主要由离心力和装配预紧力引起，但优化前后的最大变形量基本一致，约为0.243 mm。优化前后的动力涡轮转子全局等效应力分布也基本一致（见图8），最大等效应力位置也没有发生变化，均在圆弧端齿连接部位。这表明本次优化设计没有对除圆弧端齿之外的其他转子部位产生影响，尤其是没有影响转子的整体变形和整体应力分布。

对比图9～ 图14 的等效应力、径向应力、周向应力可知，无论是凹齿还是凸齿，由于开有螺栓孔，减少了凸齿和凹齿的部分齿形，在齿根过渡圆弧与螺栓孔边界的应力均较大，可见螺栓孔对圆弧端齿结构的完整性产生了一定削弱作用，造成了局部应力集中。对于凹齿而言，螺栓孔对齿形中部侧边产生了较少削弱，主要是对端齿底部基体产生了较大削弱作用；而对于凸齿，螺栓孔对整个齿形中部都有较大的削弱作用，对端齿底部的基体却削弱较少。因此，在圆弧端齿的凹齿和凸齿啮合承受工作载荷时，螺栓孔对圆弧端齿齿底的强度削弱影响要比对齿本身的大。

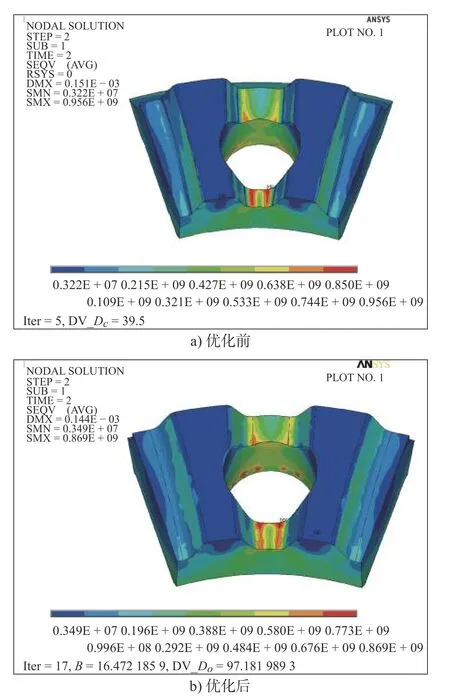
图9 优化前、后的凹齿圆弧端齿等效应力分布图

图10 优化前、后的凸齿圆弧端齿等效应力分布图

图11 优化前、后的凹齿圆弧端齿径向应力分布图

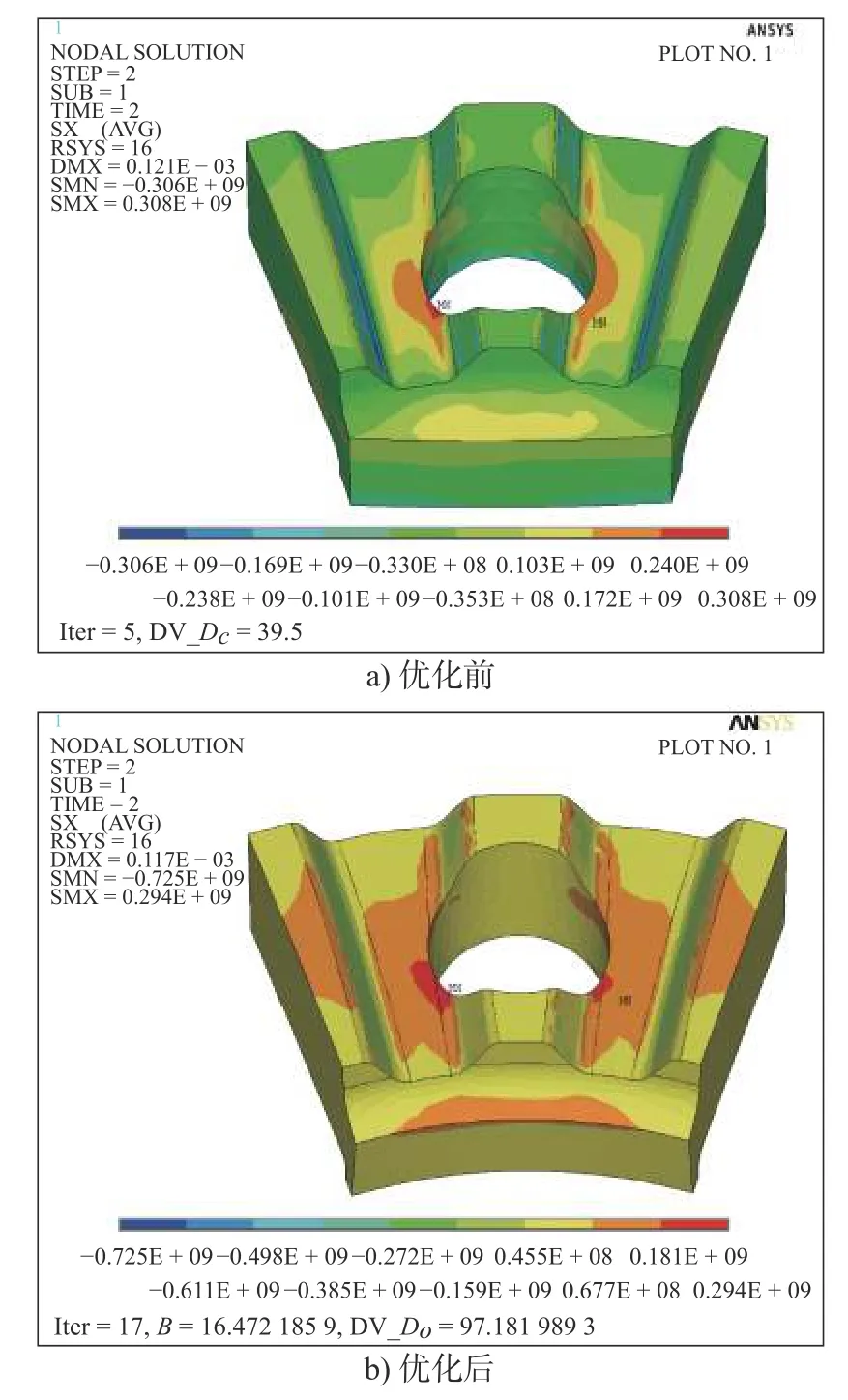
图12 优化前、后的凸齿圆弧端齿径向应力分布图

图13 优化前、后的凹齿圆弧端齿周向应力分布图

图14 优化前、后的凸齿圆弧端齿周向应力分布图

另外，在初始模型中，螺栓中心孔位置Dc比端齿的节圆直径Dm小2 mm，螺栓孔位置靠近内径，使得靠近内径侧接触部位的承力面积小于外径侧，因此圆弧端齿的等效应力峰值靠近内径侧。优化后，螺栓孔分布位置与端齿节圆直径更趋接近，使得端齿靠近内径侧与外径侧的接触部位的承力面积比例更加匹配，因此改善了靠近内径侧的应力峰值，其齿根的应力分布也得到了改善。对于凹齿圆弧端齿，优化后的等效应力峰值由优化前的956 MPa 降低为869 MPa，降低了9.1%；周向应力分量所占比重最高，与等效应力分布趋势总体上一致，最大值均发生于齿根过渡圆弧处，并且靠近螺栓孔，其应力峰值均低于材料的屈服极限；最大周向应力由优化前的990.8 MPa 降低到870.7 MPa，降低了12.1%；接触面最大接触应力由优化前的829.4 MPa 降低到459.3 MPa，降低了44.6%，但平均挤压应力和平均剪切应力有所增加，分别由203.4 MPa 增加到225.6 MPa、101.4 MPa 增加到111.3 MPa，增加幅度不明显（约10%）。这是由于优化后的外径尺寸变小，齿宽也有所降低，接触面积的降低导致接触平均挤压应力和平均剪切应力有所增加，但均在设计约束条件的范围之内，均能满足要求。

从图15 的接触状态分布图可知，接触面大部分处于相对滑移区域，在非螺栓孔的最大接触应力附近出现局部粘着区域。由图16 和图17 接触面情况可以看出，最大接触应力发生在接触面边缘，靠近内径的位置。对于滑移量大小，最大值发生在螺栓孔附近，有26.5 μm 的滑动，整体上看，螺栓孔附近的接触面区域滑移量偏大，这是由于螺栓孔对接触面整体刚性的削弱，导致螺栓孔周围接触区域变形变大，滑移量明显比非螺栓孔接触面大。

图15 端齿（凹齿）接触面接触状态分布图

图16 优化前、后的端齿（凹齿）接触面接触压力分布图

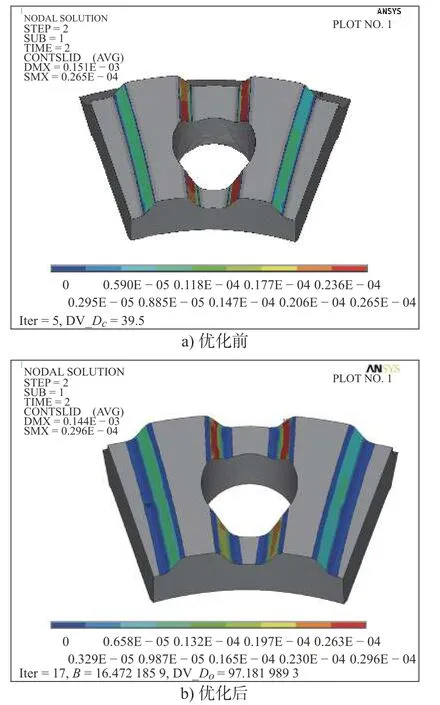
图17 优化前、后的端齿（凹齿）接触表面滑移分布图

3 结论

1）对于拉紧螺栓连接的圆弧端齿结构，螺栓孔的开设会对圆弧端齿结构的完整性产生了削弱作用，且螺栓孔对圆弧端齿齿底强度的削弱影响要比对凹（凸）齿本身的大；螺栓孔的径向分布位置对圆弧端齿的应力也有一定影响，将螺栓孔径向分布在圆弧端齿节圆直径附近对降低应力和改善应力分布状态均有利。

2）本文原始方案的圆弧端齿结构能够满足静强度要求，也基本能满足寿命要求，但在齿根过渡圆弧与螺栓孔边界的应力均较大，存在一定的应力集中，使得设计寿命裕度不大。

3）以外径和齿宽为设计变量，对圆弧端齿进行结构优化设计结果表明，在原始方案结构尺寸的基础上，适当调整外径和齿宽，端齿的最大等效应力降低了9.1%，端齿工作面最大接触应力降低了44.6%，提高了设计寿命。