风力机叶片翼型俯仰与动尾翼耦合运动数值仿真

李松林，朱卫军，孙振业，陶秋晗，曾明伍,3

（1.东方电气风电股份有限公司，四川德阳 618000；2.扬州大学 电气与能源动力工程学院，江苏扬州 225127；3.西安交通大学 航天航空学院，西安 710049）

新一代风力机正趋于大型化发展，无论是内陆低风速风力机的推进和海上风电的技术创新，风力机叶片尺寸的不断增长给气动载荷设计提出了很高的要求。风力机叶片受到湍流脉动载荷的影响、风切变、塔架阴影和偏航误差。这些影响因素组成复杂非定常气动载荷使叶片产生变形和振动。高疲劳载荷和极端负荷条件的下运行的风力机设计成本更高，并且维护成本和系统可靠性更差。为了调节功率输出和降低系统载荷，现代风力机普遍采用了自动变桨和自动偏航的功能。然而，传统的变桨和偏航控制系统需要很大的驱动扭矩，面对大型风力机，系统调节的灵敏度受到叶片的大质量和惯性的限制，系统在实际上无法快速补偿时间尺度较小的湍流运动带来的湍流脉动载荷，因此实际上疲劳载荷很难有效地消除。

对于未来大型风力机的设计，智能叶片被认为是大幅度降低风能成本和提高风能利用效率的最优前途的方法[1]。尾缘襟翼广泛应用与飞机，在起飞时增大整体升力，降落时摆动襟翼角度增加飞行阻力。图1 中显示采用动尾翼（在风能领域经常被称为动尾翼）的风力机叶轮示意图。通过改变叶片后缘的主动控制机构，使得叶片在主动变桨的同时可以针对较小的湍流变化相应的控制尾翼的角度，从而减少叶片所承受的空气动力载荷。可以预见，未来大型叶片将出现同时进行变桨和变尾缘襟翼的运行形式。余畏等[2]在FAST/Aerodyn 代码中加入柔性尾缘襟翼控制器,成功实现了叶片在湍流中的降载。变尾缘襟翼包含了动尾翼、动尾翼与变桨同时运动的复杂模式。采用尾缘襟翼实现升阻力的实时调节功能，在失速之前，尾翼向下运动时翼型整体升力提高，对应的零升力功角变小，这种效应近似于增大了翼型的曲面弧度。与之相反，当襟翼向上运动时，翼型段的气动性能下降。通过实验观测，尾缘襟翼在一些工况下还能够减少翼型的阻力[3]。

图1 动尾翼风力机叶片

可应用计算流体方法（Computational fluid dynamics,CFD）和风洞实验研究俯仰运动对翼型的影响。关于俯翼型仰运动CFD 仿真方面，国内学着进行了充分而精确的研究。谢凯等[4]对直升机二维翼型SC1095的俯仰、挥舞、摆振耦合运动进行仿真，采用ICEM软件生成嵌套网格并求解雷诺平均的NS 方程（RANS）。嵌套网格可以保持翼型边界层的贴体网格，实现翼型的俯仰旋转运动，避免了壁面边界层网格重构。徐佩等[5]采用Star-CCM+和重叠网格技术，对NACA0020翼型的俯仰和升沉耦合运动进行RANS 仿真。张一楠等[6]对有仿鯨鱼鳍前缘的翼型段的俯仰运动等进行了风洞试验，结果表明仿生设计改善了翼型动态失速特性，降低叶片极限载荷的产生。

关于动尾翼对风力机翼型的影响，国内学着也进行了一些研究。郝文星等[7]将瞬态风速导致的升力与给定升力的差作为控制信号，控制襟翼在Fluent软件中摆动，通过Fluent 软件的网格弹性变形实现襟翼偏转，研究了襟翼最大偏转速度、襟翼动作延迟时间对控制效果的影响，发现延迟时间的影响较大。李传峰等[8]采用CFD 研究了动尾缘襟翼的偏转角频率对气动性能的影响，发现尾缘襟翼降载的能力随着角频率的增大而减小；折合频率的大小可作为非定常气动特性出现的判断准则。未来智能风力机叶片会实现边桨距和动尾翼的联合控制，然而，同时考虑翼型的俯仰运动和动尾翼偏转的耦合数值模拟较少。这是由于传统的贴体网格CFD 方法，在应对翼型整体俯仰外加尾缘局部变形时存在一些挑战。为了精确地研究后缘襟翼翼型的物理效应，本文将采用传统贴体网格结合浸入边界（Immersed boundary,IB）的计算方法[9-14]。该方法采用标准有限体积法求解翼型主固定部分周围的绕流，而采用边界浸入法在曲线网格上模拟可运动的后缘襟翼。其中，翼型的俯仰运动通过旋转网格坐标系来实现，尾缘襟翼同时参与俯仰运动和相对的柔性摆动。

1 数值计算方法

1.1 浸入边界法

IB 方法专门用于处理任意运动中复杂物体的流动问题。这个想法最早是由Peskin[9]应用于研究心血管系统中的低雷诺数流动弹性边界。在高雷诺数计算方面，文献[10]采用S-A 单方程湍流模型和k-ω Wilcox 两方程模型进行了比较计算。本文介绍雷诺平均法（Reynolds averaged navier stokes,RANS）结合浸入边界的数值表达方法。NS 方程的动量方程和连续方程为

方程区别于传统NS 方程的表达形式，其中动量方程中添加了一个源项fi。该源项表示了非贴体网格中,浸入边界部分表达的虚拟外力作用。如图2和图3 所示，全贴体网格计算中，物体边界的受力通过求解速度与压力耦合的方程得到，主要体现为压强力和黏性力。在非贴体网格中，由于缺失物体壁面黏性边界条件，如方程不做额外变化，该计算区域将等同于其它的外流场区域。

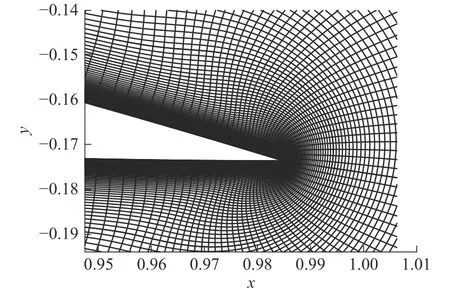
图2 全贴体网格

图3 贴体网格与浸入边界网格的混合

式（1）中，将速度的时间导数离散化，将其余项移到方程右侧合并，并把右侧合并项表示为RHS，可得

假设迭代次数n=1 时速度场为已知，即初始条件给定，并且浸入边界的各个几何点上的速度uib已知，则临近浸入边界网格节点上的的速度由流场中的速度和边界运动速度插值求得，即

因此，式（2）与式（3）建立了速度和外力的迭代关系。

1.2 非惯性坐标系统

流体计算中常常有物体自身做复杂运动的情况，理论上可以采用上述浸入边界的方法求解整个物体周边的流动场，比如当前情况下翼型的复杂运动。但是全部采用浸入边界方法将大大增加计算量。采用旋转坐标系结合尾缘襟翼位置浸入边界方法将大大提高计算效率和精度。在旋转坐标系下，式（1）成立必须满足前提条件，即流体质点的加速度必须是相对于惯性坐标系下的加速度。在旋转坐标系下，式（1）的速度导数项（即质点加速度）必须包含额外的加速度项，即

式中：|Ω|为旋转速度；r为质点与旋转中心的距离矢量；V为质点运动的速度矢量。对于当前的二维翼型计算，展开各个向量积可得：

式（5）各项相加作为动量式（1）的添加项放入右侧，此方程将结合IB 方法求解翼型俯仰运动与动尾缘襟翼的叠加效应。

1.3 NS 方程求解流程

计算程序采用速度压力耦合方程，应用 SIMPLEC/PISO 方法和多重网格策略。在动量方程中首先用预猜测的压力作为预测因子求解方程，然后，用连续方程为约束，得到压力修正方程。时间和空间差分均采用2 阶精度，其中空间差分采用有限体积法，而湍流扩散项采用中心差分格式求解。在校正步骤，采用Rhie Chow 插值技术是用来抑制速度压力耦合求解带来的数值振荡问题。在结构化网格中结合IB 方法，方程添加外力项如式（1）所示，在每个迭代步长中更新速度场，从而更新外力项。其具体的计算流程如图4 所示，首先初始化流场，应用经典流体力学中的边界条件和初始值，然后仅在第一个计算步长读入IB 外形几何数据，该组数据通常需要根据点的密集程度重新插值组合。在每一时刻，判断浸入边界的内外计算节点，如浸入边界相对于翼型本地坐标的运动速度为零，则该过程仅需执行一次。由于RANS 方法求解k-ω方程时采用的壁面边界条件与垂直距离有关，因此在虚拟的IB 边界上同样需要求解壁面垂直距离。根据给定的IB 运动方程（采用主动控制方法的除外），求得该时刻IB 上每个点在水平方向、垂直方向的位移和速度，如尾缘襟翼为静止状态，则位移和速度均为零。判断下一步尾缘襟翼是否运动，如运动则返回，重新区分并标识IB 分割线的内外计算网格节点。在IB 附近的网格点上进行速度的插值运算，采用IB 上的运动速度与流场内部相邻点的速度进行插值。根据该速度值更新外力项，将此外力合并至动量方程的源项中，进一步更新流场。下一个步长，如尾缘襟翼持续改变位置，则重复进行迭代计算，直至设定的总迭代步数，最后积分求得升阻力。

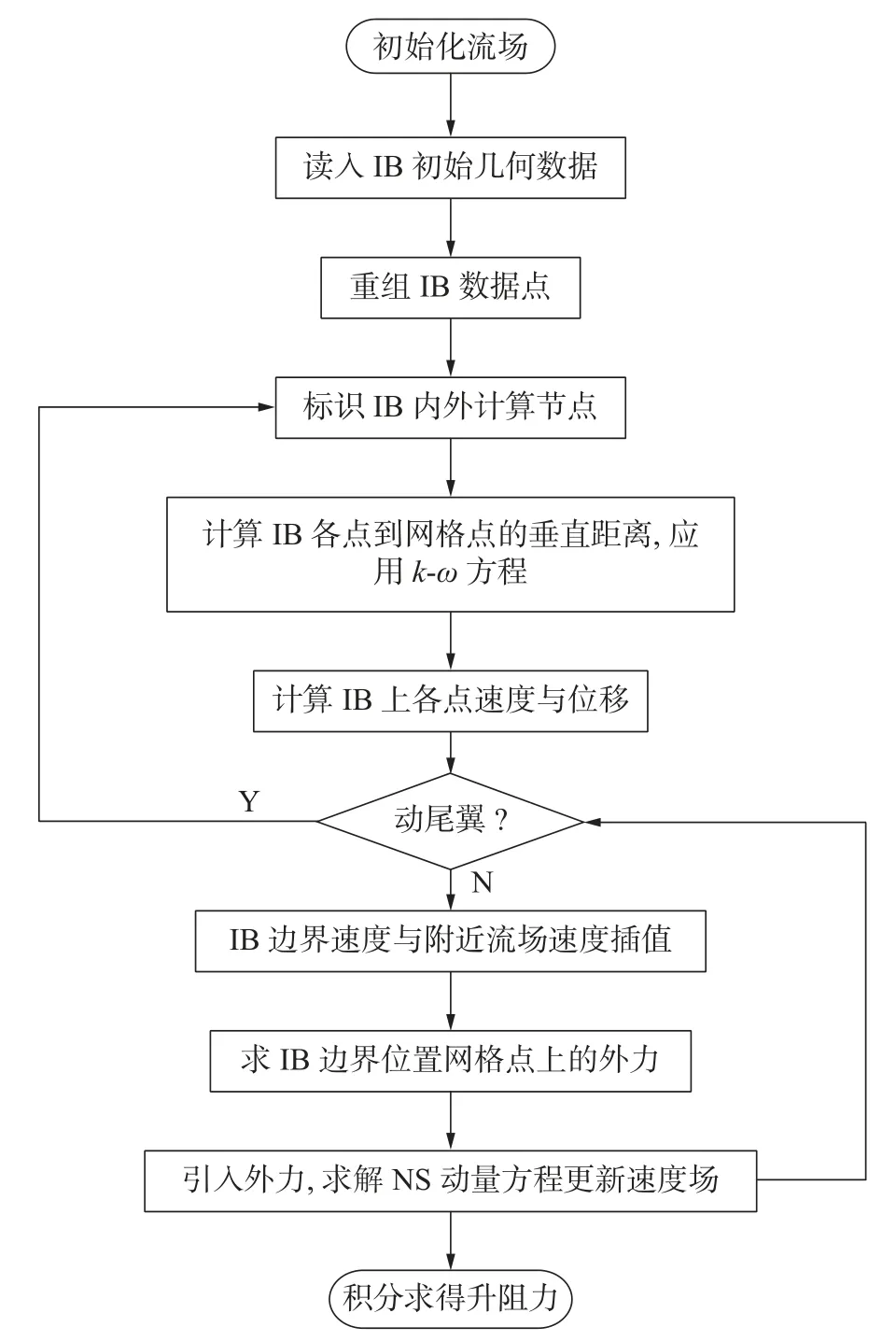
图4 结合浸入边界方法的NS 方程求解流程图

2 尾缘襟翼运动方程

当前的模拟中，尾缘襟翼部分由函数表示，该函数能够较好地描述翼型尾缘襟翼的柔性变化。动尾翼部分各个坐标点沿着x轴和y轴的位移变化式为：

如图5 所示，a、b两点始终固定，其余各点按照式（6）和式（7）的定义变化位置。

图5 尾缘襟翼弹性运动示意图

当迭代步长为n+1 时，新位置坐标等于前一步的位置坐标加上单位时间 ∆t内产生的新位移，即和中几何边界的运动速度为时间的函数，即考虑存在任意运动形式的情况。方程中的幂指数p描述了尾缘襟翼的柔度，当p=1 时，尾缘襟翼做刚性运动，当采用幂指数为p=2 时的运动形态如图5 所示。

3 结果分析与比较

3.1 尾缘襟翼运动

实践中,由于贴体网格的计算效率更高,静态翼型无需采用IB 方法进行模拟。然而作为IB 方法的验证，贴体网格算法可以作为一种参考方法进行对比。图6 显示了NACA0012 翼型的表面压力系数分布，雷诺数为5×105，来流攻角 α=4◦。由图6 可知，在静止状态下，采用贴体网格和浸入边界方法计算所得到的压力分布结果几乎完全对应。采用IB 方法在尾缘部分需要的网格要多于贴体网格，若采用IB 方法模拟整体翼型，其计算效率将低于传统贴体网格算法。

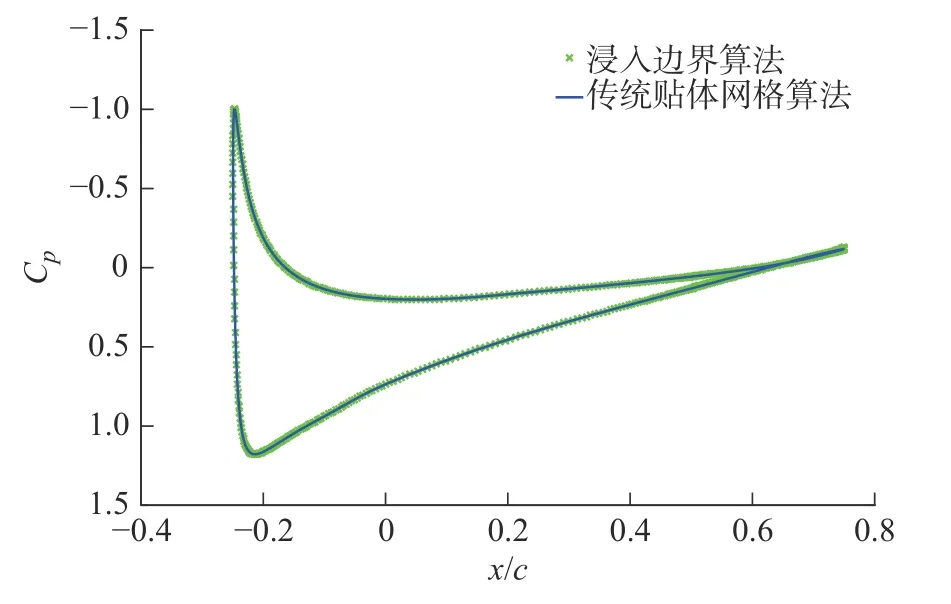
图6 尾翼静止时贴体网格和混合网格对比

对于流动中包含复杂几何外形或物体做复杂运动的情况，IB 方法展现了其强大的灵活性。对于运动的尾缘襟翼流场计算，传统的贴体网格算法必须在每个时间步长上根据翼型新的形体重新生成新的网格，如此大大增加了计算的时间。采用IB 方法将保持固定的网格，尾缘襟翼部分则在网格中做相对运动，其运动的形式可以由任意方程提前给定。比如，当前的尾缘襟翼的运动采用正弦函数描述，即

式中：δo为初始角度；A为最大位移；k1为折算频率（Reduced frequency）；φ 为相位角。结合式（6）和式（7）关于位移的函数描述可以得到尾缘襟翼每个点的运动速度：

式中：r(t)为第i个边界点距离转动中心的距离，在每个时刻，尾缘襟翼产生的线速度分解为水平方向和垂直方向的速度分量

图7 中显示了某一时刻NACA0012 翼型尾缘襟翼运动时的水平速度分量云图和速度流线图，图8中可见升力的变化同样近似于正弦，这也与主观预期一致。当前计算采用入流功角为4°，雷诺数为1.63×106，翼型尾缘襟翼部分大小为整体弦长的22.6%。由图8 的升力变化结果可以看到，翼型升力的变化主要取决于几个条件：尾缘襟翼相对于整体翼型的大小、摆动的幅度和摆动的频率。翼型襟翼的运动方式可以提前给定也可以根据升力的大小自动调节，后者涉及到升力的主动控制，即给定控制算法在每个时间步长中判断尾缘襟翼下一步的位移量，从而使升力不断接近目标量。当前关于翼型与运行条件的选取是为了与风洞实验进行真实对比。下文将模拟翼型的复杂运动并与风洞实验进行比较。

图7 尾翼运动时水平速度分量云图

图8 翼型升力曲线

3.2 尾缘襟翼结合俯仰复杂运动

为了验证动尾翼计算的精度，本文将对比Krzysiak 等[15]的风洞实验结果。在文献[15]中，作者对NACA0012 翼型进行了风洞气动实验，并与半经验的理论模型进行了对比，由于模型建立在无粘流动基础之上，在许多工况的对比中发现理论模型与实际相差较大，由此本文展开数值计算方法模拟翼型复杂的耦合运动。如图9 所示，该翼型的俯仰旋转中心位于距离翼型前缘位置0.35C处，尾缘襟翼的长度为0.226C，其旋转中心位于0.2C处。俯仰与尾缘襟翼运动函数组合如表1 所示。

表1 俯仰与尾缘襟翼运动函数组合

图9 风洞实验中NACA 0012 翼型和可动襟翼[15]

入流攻角采用正弦周期性函数表示为

组合1～组合3 中，入流攻角的初始位置为 4◦，俯仰的最大振幅为 6◦；尾缘襟翼初始位置为 0◦，摆动最大幅度为5.4◦。实验中分别采用了3 组相位差：148◦，298◦，357◦。图10a）、图11a）和图12a）中分别显示了计算模拟采用的动态函数，其中横坐标为攻角，纵坐标为尾缘襟翼角。由于相位不同，3 组情况下运动形态具有显著差异。图10b）、图11b）和图12b）中分别比较了单独俯仰运动和组合运动的动态升力。单独俯仰运动时，翼型的升力呈经典的“O”型闭合循环，数值模拟与实验整体拟合较好。当尾缘襟翼一起运动时，升力曲线在初始攻角附近形成交叉，呈“∞”型闭合循环，结果整体吻合。需要指出的是，由于实验机构的振动和伺服机构的缺陷，实际的俯仰和尾缘运动趋近于正弦函数，但是仍有明显的差异[15]（图13 和图14），这些也是导致计算与实验存在一定误差的原因之一。其次，根据计算流体的模拟经验，对于雷诺平均方法而言，模拟翼型的大攻角和失速区间结果精确度通常较低，不同湍流模型之间往往也差别较大。适当的降低俯仰和尾缘襟翼运动的幅值可以改善计算模拟的准确性。组合4和组合5 中变化了运动函数组合，其中两种运动的幅值均有所降低。图13 中，动态升力的比较与实验基本吻合。由于伺服机构的误差，组合4 中实验所测的攻角范围超出了最小极限值−0.5°较多。图14中，动态升力的变化无论从趋势上还是幅值上都实现与实验较好的吻合。

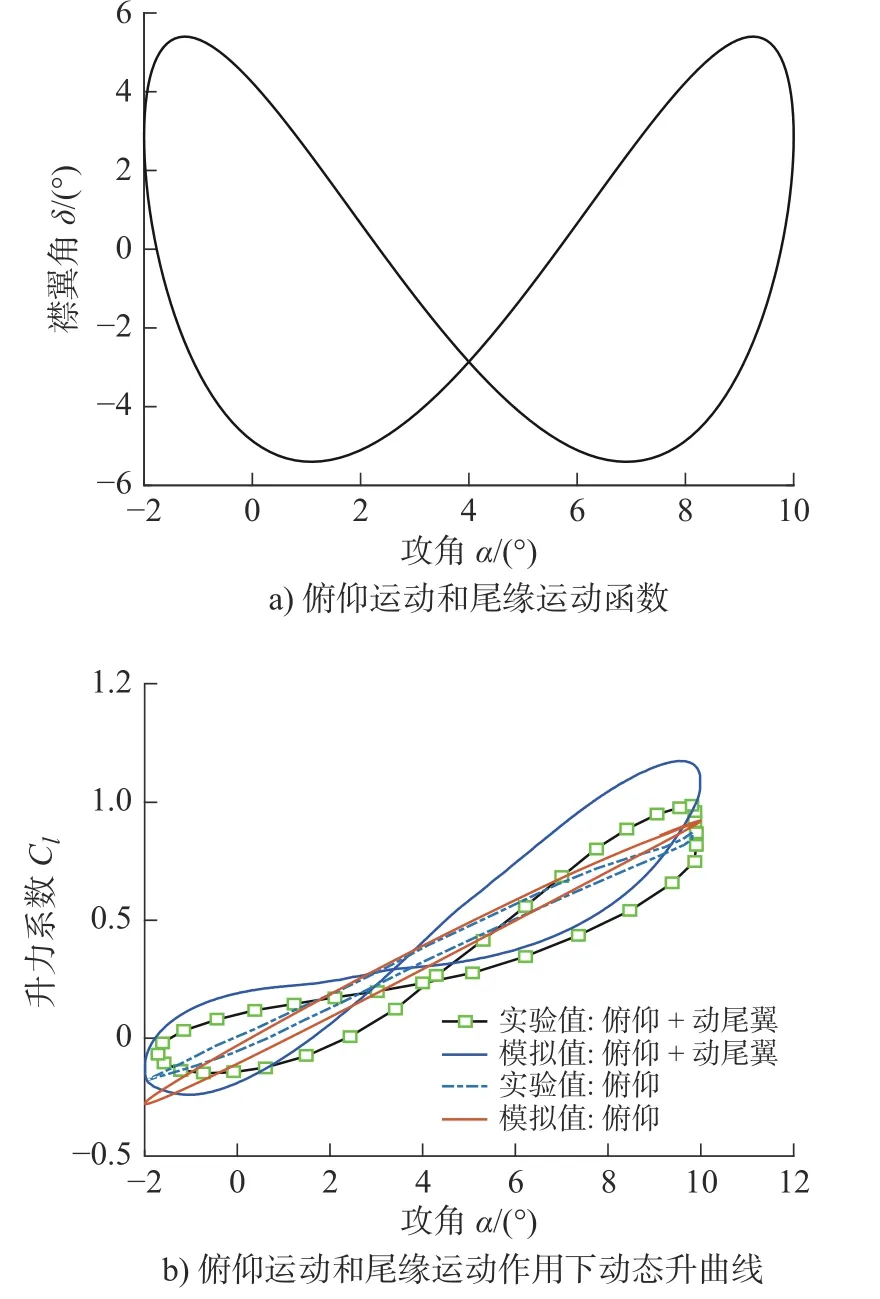
图10 组合1 计算结果

图11 组合2 计算结果

图12 组合3 计算结果

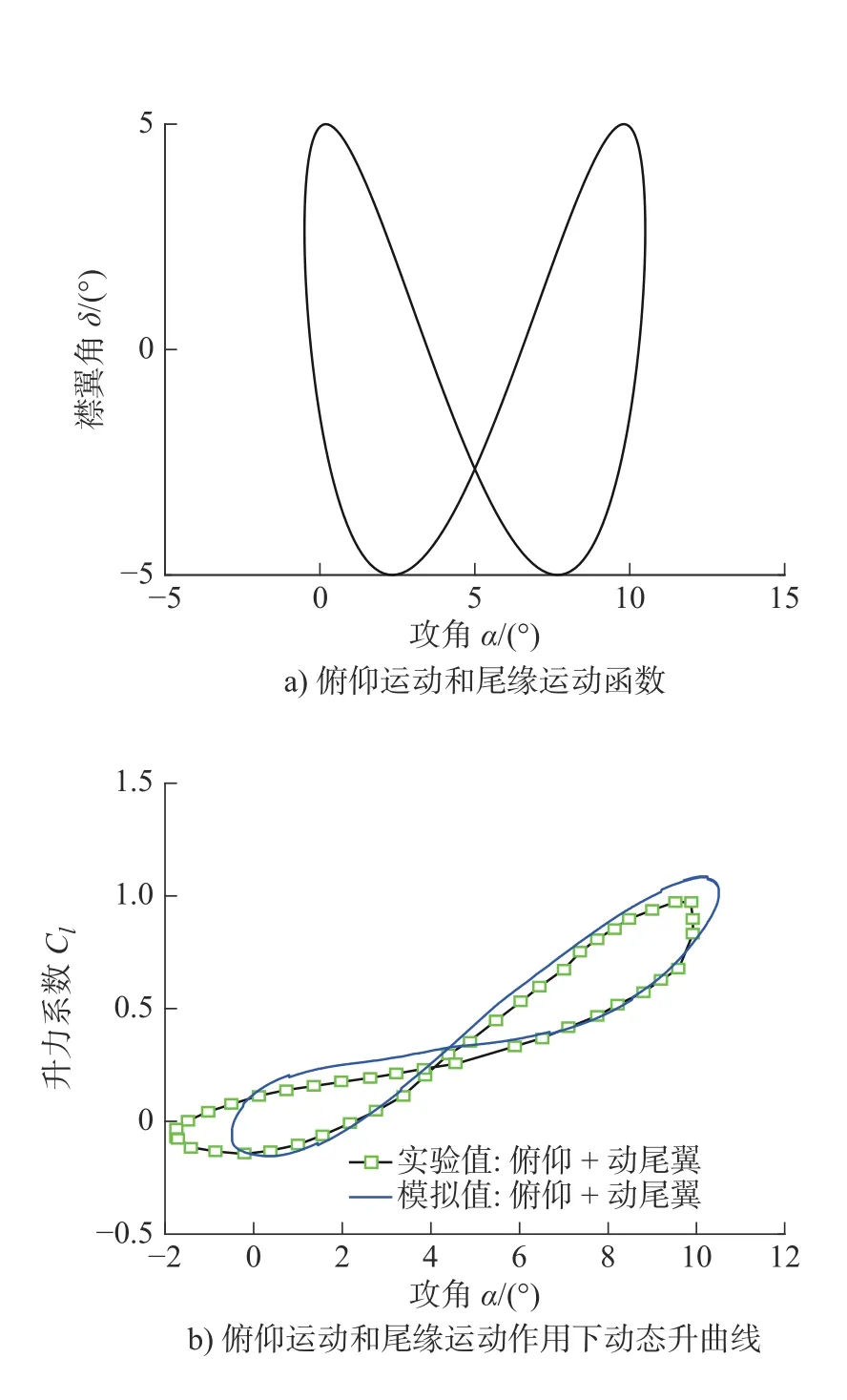
图13 组合4 计算结果

图14 组合5 计算结果

4 结论

本文针对风力机叶片发展大型化和智能化的趋势，从翼型变桨控制结合动尾翼控制的策略出发，探索了一种基于浸入边界方法的实践应用。为了与风洞试验进行比较，本文的研究中，变桨运动和尾缘襟翼运动均采用正弦函数表达方式。叶片的实际的运动形式应完全由给定的升力、阻力等目标量进行反馈和输出控制。本文采用了5 种不同组合的桨距角变化和尾缘的变化形式，结果显示出两者的组合形式带来的翼型升力变化是显著的，同时结果与实验数据相符。