航空发动机振动传递特性研究进展

汪 才，艾延廷，陈仁桢，张凤玲，艾辛平

（沈阳航空航天大学航空发动机学院，沈阳 110136）

0 引言

目前，航空发动机发展的迫切性与重要性受到相关学者的高度重视。近年来整机振动传递特性技术已成为研究热点。据统计，发动机在使用过程中70%以上的故障源于振动[1]，且因振动故障返厂占总台数的60%以上[2]。由于发动机结构复杂导致传递规律难以摸索，加之传递信号在传递过程中被削弱，机匣信号测点难以选取等因素，准确刻画发动机振动传递特征及动力学响应特性十分困难。陈予恕等[1]指出发动机整机振动机理研究是航空领域的重大课题。

目前旋转机械振动响应主要来源于转子-轴承系统损伤、转子-机匣系统碰摩等故障，此类振动信号展现出明显的非线性特征，郑丽等[3]、艾延廷等[4]、Ewins 等[5]学者均对航空发动机整机振动进行了综述分析。发动机转子-轴承-机匣系统振动信号高度耦合，且受发动机结构和工作条件的制约，对振动传感器提出极高要求，测试方案难以实现。另外，振动传递路径分析方法在发动机领域并未系统开展。发动机整机振动传递特性研究分为振源研究和传递路径研究2 大类。若想实现航空发动机整机振动的有效抑制，必须以整机振动的振源为出发点。发动机振源主要来源于双转子系统不平衡和不对中故障、转子-轴承系统缺陷故障、转子-机匣系统碰摩故障、气流激振以及局部结构共振等，结合发动机整机结构动力学通过对振源的抑制可以有效抑制振动载荷的传递。此外，利用传递路径分析（Transfer Path Analysis，TPA）、工况传递路径分析（Operation Transfer Path Analysis，OTPA）、扩展工况传递路径分析（Operational-XTPA，OPAX）找到振动传递路径，通过对振动传递贡献度较高的路径进行优化设计可以有效抑制和改善整机振动。

本文分类综述了航空发动机整机振动传递特性研究成果，搜集整理了应用于转子-轴承-机匣-吊挂系统振动传递分析方法。并针对发动机振动传递特点，分别对振源研究和传递路径研究2 类抑振方法及相关研究成果进行了分析。

1 振源分析

长期以来，引起航空发动机振动的因素多且复杂，航空发动机故障振源分类如图1 所示。原发故障引发的振动一类是属于转子系统随转速变化的规律性激振源，例如转子不平衡、不对中引起的激振力，转子-机匣系统碰摩、转子-轴承系统缺陷、传动齿轮系统故障等。另一类是与转子系统转速无关的非规律性激振源，此类激振形式较为复杂，出现时间及频率难以预测，例如机械松动、振荡燃烧、压气机喘振、叶栅尾流激振等。本节对以上代表性振源进行分类，对振动机理研究进展及振动表征进行总结。

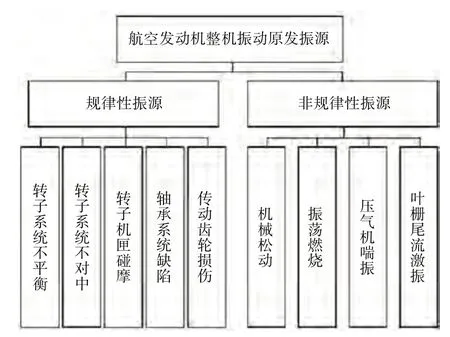
图1 航空发动机故障振源分类

1.1 转子系统不平衡、不对中

不平衡是转子系统中最常见的故障类型之一。由于转子材质不均匀、热变形、质量脱落和在运行过程中有介质粘附到转子上均会使实际转子质心点与形心点位置产生偏移，继而使得转子出现质量不平衡。不对中故障可引起转静子碰摩，对航空发动机的稳定运行具有极大的危害。转子不平衡、不对中会使盘-轴系统产生离心力引起整机振动。航空发动机等大型旋转机械中不对中故障占转子系统故障的60%以上[6]。不论是普通的旋转机械还是精密的航空发动机转子系统，不对中故障的定量分析以及其在线抑制均为难以攻克的问题。故障信号传递衰减如图2 所示，由于故障特征信号在传递过程中不可避免的衰减，实际情况下难以提取到有效的转子振动信号，所以仍有许多工作需要深入开展。

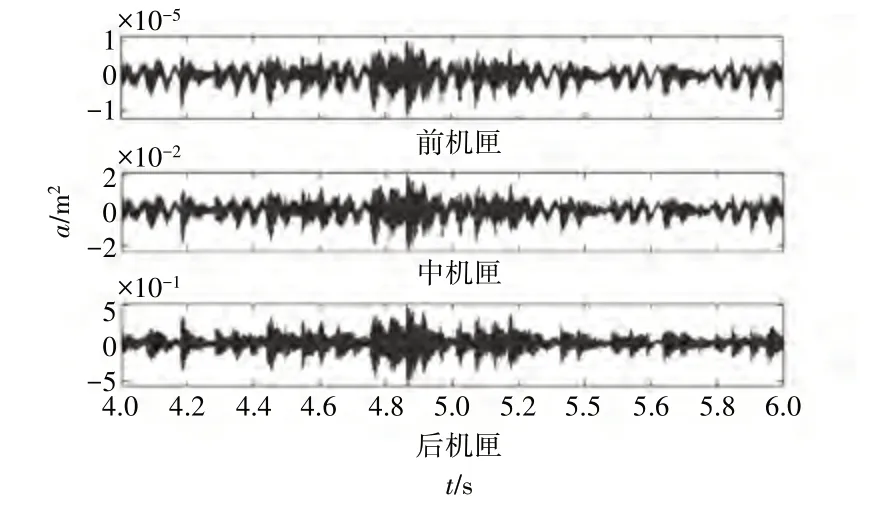
图2 故障信号传递衰减

关于转子故障系统动力学特性研究已经有一定进展，近年来相关学者将研究目标转向航空发动机转子系统不平衡、不对中导致的非线性动力学分析与装配优化问题。何俊增[7]采用Newmark-β 法求解双转子耦合故障动力学模型，研究了双转子系统不平衡、不对中对系统动力学特性的影响，研究表明不对中故障包络谱频率成分以2 倍频为主，不对中对系统振动特性影响如图3 所示，其轴心轨迹呈水滴形，对于分析转子故障类型具有重要意义。李自刚等[8]、杨洋等[9]研究了转子间平行不对中故障的柔性转子系统非线性动力学特征，推导了非线性油膜阻尼力条件下多转子系统的动力学模型。

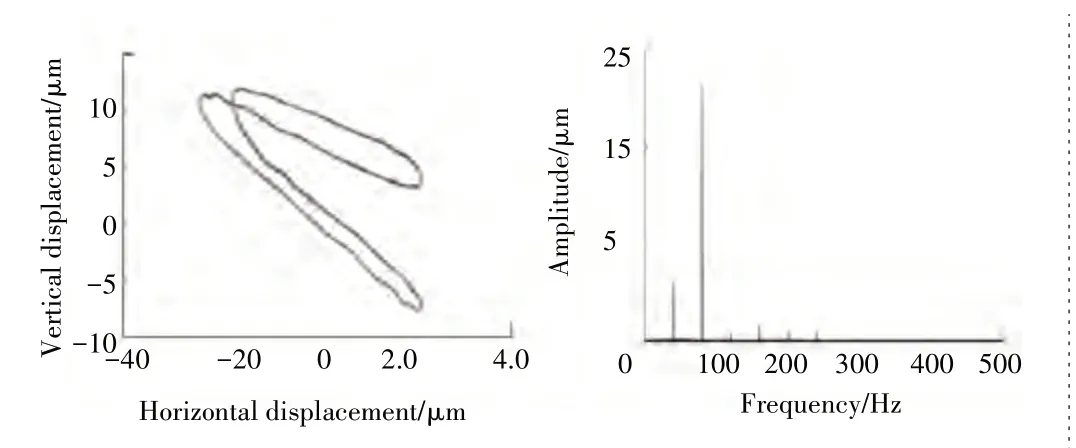
图3 不对中对系统振动特性影响

为了研究转子不平衡、不对中作为激振源时系统振动特征，首先需建立航空发动机平衡转子系统模型。理想条件下，叶片装配在发动机叶盘上，以叶盘中心为原点建立笛卡尔坐标系，理想叶片位置如图4 所示。其中，θB为叶片装配角，r为叶盘半径，l为质心径向距离。则叶片装配矢量传递矩阵为

图4 理想叶片位置

将传递矩阵代入式（1）得

式中：ZB为OB对应的叶片装配平面高度。

将式（3）～（6）代入式（2）得θB处空间叶片矢量为

基于理想装配叶片质心关系式，刘洪慧[10]建立了双转子系统装配不平衡、不对中预测模型，使用坐标变换结合静、偶不平衡量实现了对转子不平衡的精准预测，并基于预测模型使用遗传算法对双转子系统的装配过程进行优化，具有一定工程意义。刘泽伟[11]针对发动机双转子连接接触面误差提出优化转子同轴度进而建立不平衡矢量投影模型的双目标优化装配方法，为转子设计装配提供参考；宋培培[12]研究了转子不对中故障机理，建立转子偶尔动力学模型，计算表明转子弯曲与质量偏心故障特征基本相同，在同时存在2 种故障时位移幅值非线性叠加。该研究为进一步制定航空发动机不平衡、不对中标准奠定理论基础；肖平欢[13]基于盘轴结构系统转子不平衡量传递机理建立多级盘片不平含量传递模型，分析了因叶盘质量问题和装配误差对系统产生的影响，在此基础上提出模型优化方法，通过仿真分析了优化方法的可行性。部分学者以发动机主动磁轴承（Active Magnetic Bearing，AMB）为研究对象，研究主动磁轴承与转子不对中故障导致设备过度振动问题；Rajiv 等[14]提出一种非接触式位移传感器与转子中心偏移的数学模型，Prabhat 等[15]、Siva 等[16]分别建立了四自由度航空发动机主动磁轴承-转子系统模型提出失准方法估计电磁轴承的动力学表征，针对转子响应和系统误差对算法进行了验证。在此基础上Prabhat 等[17]确定了磁力轴承-转子不对中的刚度系数，基于Timoshenko梁理论对错位磁悬浮轴承柔性轴进行数学建模，采用动态简化方案消除系统横向转动，从数值验证了算法的鲁棒性。

1.2 转子-机匣系统碰摩

航空发动机具有盘轴结构系统，运行过程中产生转子叶片-机匣碰摩是最常见的机械故障之一，研究学者大多采用Timoshenko 梁单元和壳单元模拟含碰摩故障的系统模型，发动机盘轴结构系统如图5 所示。近年来，更偏向于基于拉格朗日方程建立非线性动力学方程，采用有限元方法计算系统非线性动力学响应，研究方法多样化、研究内容具体化使得时频特性分析更为准确。马辉等[18]、路阳[19]、刘诗宇[20]基于ANSYS 有限元模型建立转子-盘-机匣耦合系统模型，分析了定侵入量条件下系统的振动响应。结果表明在定侵入量条件下，高转速碰摩情况下系统碰摩特征减弱，频率成分减少，不同转速下的法向碰摩力如图6 所示。杨洋[21]以Jeffcott 转子为研究对象，提出新型碰摩力的数值计算方法，可以实时根据侵入深度对新型碰摩力模型进行修正。

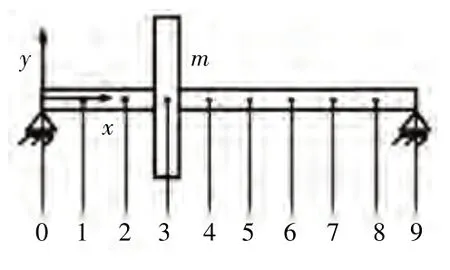
图5 发动机盘轴结构系统

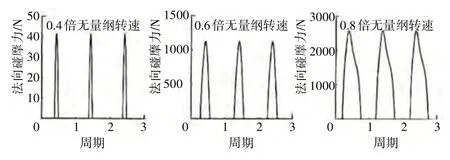
图6 不同转速下的法向碰摩力

Yu 等[22]、Chao 基[23]于拉格朗日方程建立非线性系统动力学模型，采用有限元求解了系统非线性动力学响应，通过KNN 算法识别系统碰摩故障并确定故障位置；廖明夫等[24]建立了虑及陀螺力矩的转静子系统碰摩故障模型，采用延迟微分方程数值解对过程进行数值分析，研究表明剧烈的碰摩会导致转子系统出现反进动现象，最终可导致扭振失稳。马新星[25]、殷帆丽[26]、秦海勤等[27]、林学森等[28]分别采用Newmark-β法和Runge-Kutta法数值积分方法求解某型航空发动机系统动力学响应，研究发现系统发生碰摩时转子机匣测点频谱图中会出现转子倍频及组合频率，碰摩严重时会导致4 倍频激增，产生复杂组合频率成分；刘洋[29]基于FDM 和快速谱峭度方法准确提取了转子碰摩故障特征频率，高效滤除了故障诊断结果中的噪声，验证了算法的有效性并将该方法应用于故障诊断领域。侯理臻等[30]设计了刚度和频率可调的转子机匣碰摩模型并进行了不平衡持续碰摩试验，试验结果表明在风扇不平衡下转静子碰摩会激起正反进动的高次谐波，以1.5 倍频最为明显。Yu 等[31-32]、Qian 等[33]针对旋转方向和初始速度对转静子系统碰摩动力学特性展开研究，研究发现旋转方向和初始速度因素对系统动力学特性均有显著影响，反向旋转对系统影响更为显著，系统时频特性曲线表征也更加复杂；靳玉林等[34]结合发动机双转子试验台采用数值解法求解系统非线性振动响应，结果表明根据叶尖间隙可以对叶片-机匣碰摩程度进行诊断。

1.3 转子-轴承系统缺陷损伤

转子-轴承结构被广泛用于涡扇发动机设计之中[35]，由于高温、高速和重载荷，轴承极易发生损伤。轴承故障必然引起转子系统振动异常进而影响发动机的安全性与可靠性[36-37]，因此，对转子-轴承结构典型故障进行准确的动力学建模及振动分析，揭示中介轴承典型故障特征，转子-轴承系统设计和轴承缺陷故障诊断具有重要意义[38-40]。建立有效的轴承动力学模型是转子—轴承系统动力学建模的必要基础。在早期动力学建模中，McFadden 等[41-42]、Su 等[43]分别建立了滚动轴承单点和多个缺陷的脉冲序列模型，分析了载荷周期及传递路径对于滚动轴承振动特性的影响；Qin 等[44]提出一种复杂的多自由度滚动轴承故障动力学模型，并采用4 阶Runge-Kutta 法求解，获取了不同径向载荷、转速以及轴承缺陷条件下，滚道和保持架的振动响应；Jayakanth 等[45]以滚珠轴承为研究对象评估内圈缺陷和外圈缺陷对于机械性能的影响；Sameera 等[46]采用改进的2 自由度滚珠轴承动力学模型进行深入分析，得到了速度、载荷、缺陷尺寸和缺陷位置对轴承响应特性的影响；Parmar 等[47]通过数值模拟和试验得到了局部缺陷的滚动轴承振动响应规律，研究滚动轴承的缺陷深度、倾斜轨迹和偏移轨迹对轴承振动特性的影响；Bastami 等[48]建立了含轴承外圈及滚柱缺陷的滚动轴承模型，通过该模型提出了一种缺陷尺寸的估算方法；Jiang等[49]考虑滚动体和缺陷面积3 维关系研究了缺陷尺寸对接触形式的影响，比较了不同接触形式下，滚动体所受接触力的变化；Niu等[50]提出的模型考虑了滚子的相对滑移、缺陷尺寸以及接触力方向，并分析了滚子缺陷沿着内、外滚道旋转时轴承的振动响应。研究学者们提出了多种轴承动力学建模方法，并证明了所提出方法的准确性。研究表明，时变位移函数能够较好描述轴承内外圈故障形式，提升轴承故障模型的准确性。

针对转子-轴承系统模型建模，近年来研究人员更偏向于通过第2 类拉格朗日方程对转子—轴承系统建模，相比于牛顿法，拉格朗日功能关系可以有效避免矢量参数对系统振动特征响应的影响。以某型双转子—中介轴承系统故障特征频率求解过程为例，双转子-中介轴承系统模型如图7所示。

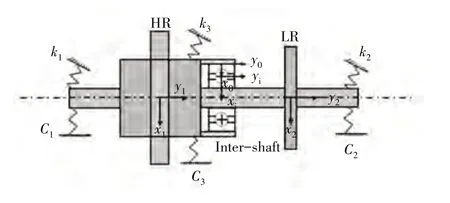
图7 双转子-中介轴承系统模型

基于非线性Hertz 接触理论，采用时变位移激励对中介轴承存在单点及复合缺陷情况进行描述，同时，考虑高低压转子自重、径向载荷、高低压转子、内圈和外圈在水平与竖直两个方向的振动，考虑由于转子不对中以及内、外圈的偏心而引起的离心力，建立8 自由度故障动力学模型。建模过程中，假设滚子不存在打滑现象。建模具体为

系统动能

系统势能

系统中瑞利耗散能

广义力虚功

式中：下标为1 的参数为低压转子的相关参数；下标为2 的参数为高压转子的参数；下标为i的为中介轴承内圈的相关参数；下标为o的为中介轴承外圈的相关参数；x和y分别为竖直与水平方向的位移；m为质量；e为偏心距；ω为角速度；k为刚度系数；C为阻尼系数；F为在对应方向的弹性恢复力；g为重力加速度；t为振动时间。以上所有参数单位均按照量纲国际单位进行计算。

对于非保守系统，考虑系统动能、系统势能、瑞利耗散能以及广义力虚功，将式（8）～（11）代入第2类拉格朗日方程，有

解得系统动力学方程组为

通过对于非保守系统，考虑系统动能、系统势能、瑞利耗散能以及广义力虚功，将上式代入第2 类拉格朗日方程可以有效避免因为矢量方向判断错误导致结果不准确，大大提高了计算效率。近年来基于使用第2 类拉格朗日方程表述集中参数模型的研究越来越受到相关学者的青睐。Yi 等[51]建立双转子系统动力学简化模型，分析了含等腰梯形槽缺陷故障系统的组合共振特性；Cao 等[52]建立了含球轴承的转子系统动力学模型，该模型考虑转子弹性变形能够有效的模拟配合间隙引起的轴承局部冲击现象。Liu 等[53-54]建立了刚性转子-滚子轴承-轴承座的较为复杂的系统动力学模型，在模型中采用半周期函数描述深沟球轴承的时变位移激励；Gao 等[55]考虑带有外滚道缺陷的中介轴承受力模型建立双转子系统的运动方程，对转子系统的振动加速度信号进行探究，但其模型考虑缺陷类型较为单一；Gao等[56]建立考虑Hertz接触力等非线性因素的中介轴承内、外圈局部缺陷的动力学模型，采用数值方法得到系统的非线性振动响应，但该研究没有考虑复合故障对非线性振动响应的影响。以上研究表明，在双转子系统中考虑中介轴承典故障是切实可行的。采用能量法可以将转子系统模型与轴承故障模型进行统一。采用Newmark-β法或者Runge-Kutta法可以对模型进行准确求解。

1.4 传动齿轮损伤

某型航空发动机齿轮传动系统如图8 所示。传动系统的工作环境十分复杂，本身复杂结构使得齿轮系统很容易发生故障。分析传动齿轮系统需要多学科包括轴承动力学、转子动力学和齿轮动力学为一体的复杂动力学特性理论基础。近年来相关学者大多基于势能法对时变啮合刚度进行精确求解，使得频谱分析更加准确。王志强[57]、王鹏等[58]采用4 阶Runge-Kutta法对集中参数模型进行Matlab编程，建立4级齿轮传动系统非线性动力学46 自由度仿真模型，进而分析时变啮合刚度对模型响应结果的影响。基于分析结果，探究了引起多级平行轴齿轮传动系统振动的重要原因。同时，通过模型振动时域响应及频谱分析，发现各级传动齿轮之间存在耦合振动现象；孟凡秋等[59]针对涡扇发动机星型齿轮传动系统建立了齿轮-转子-轴承耦合动力学模型。该动力学模型研究了输入轴和输出轴上轴承位置对星型齿轮传动系统各部件浮动量以及负载分配特性的影响。确定了输入轴和输出轴上轴承的布置方式对太阳轮和齿圈的浮动量影响较大，对星型齿轮的浮动量几乎无影响；杨昌祺等[60]、Chen 等[61]、Hong 等[62]以故障断裂中央齿轮为研究对象建立有限元模型，采用准静态法模拟齿轮啮合过程，结果表明齿轮啮合状态异常会显著提高振动应力水平；陈慧聪等[63]通过探究发动机锥齿轮体传动故障机理分析了齿轮振动特性以及动应力分布情况。根据故障原因对中心锥齿轮进行优化设计，改进后得齿轮工作稳定，持久工作条件下状态良好；Yan 等[64]基于断裂力学和非线性赫兹接触理论建立等效模型计算齿轮裂纹产生于扩展趋势，提出一种疲劳寿命预测方法，经计算与其他文献结果对比验证了该方法得可行性。

图8 某型航空发动机齿轮传动系统

近年来随着振动特征信号提取技术的不断发展，学者对于航空发动机齿轮传动系统的动力学特性刻画更加精确。钟也磐等[65]针对故障诊断问题提出一种基于Hermite 插值的加强谱峭度故障诊断方法，结合谱峭度找出特征频带，可以有效识别减速器轮毂故障，实现便捷诊断。王志强[66]、栾孝驰等[67]采用瞬态接触动力学分析方法对锥齿轮发生行波共振时的振动特征进行了准确的表征，基于声测法研究中央传动锥齿轮行波共振特征，准确预测了齿轮发生断裂故障；Guo 等[68]、Yuan 等[69]通过有限元建模分析方法模拟齿轮故障特征，采用电镜扫描、能量分析、光谱分析等试验手段进行齿轮力学性能评估。陈礼顺等[70]、姜贵林等[71]、沈君贤等[72]运用MODWPT、SR、V/EMD 等多种分析方法在强背景噪声条件下对齿轮多域故障特征信号进行分析处理，增强故障特征信号为齿轮故障诊断提供了新的方法；在此基础上，陈礼顺等[73]建立2 维特征矩阵并通过建模对稀疏矩阵范数正则进行描述，提出广义坐标优化求解算法框架，与经典谱峭度计算方法进行对比验证了算法的优越性。

1.5 非规律性振源故障概述

非规律性激振源激振形式较为复杂，出现时间及频率难以预测，例如机械松动、振荡燃烧、压气机喘振、叶栅尾流激振等。非规律性振源故障由于其随机性使研究无法定向开展，国外学者对此类振源故障研究较少，对此类故障的研究无系统整合。本节以近年来国内相关学者针对特定非规律性振源故障试验研究开展有突出贡献结论的成果展开综述。

（1）机械松动。机械松动指某一连接系统零件接合面存在间隙或联接刚度不足导致系统机械阻抗降低、配合面间距加大进而引发发动机振动过大等故障。近年来松动故障作为发动机非典型故障模式少有学者展开研究。曹树谦等[74]针对支承松动的转子—轴承系统利用优化遗传算法对松动故障动力学参数进行识别，提高了松动参数的识别效率；蒋勉等[75-76]基于非线性振动特征信号建立一种松动状态评估方法，针对松动故障机理结合MATLAB 数值计算方法计算在不同松动程度下系统非线性度的变化关系，为发动机转子—轴承系统动力学行为描述和支承松动状态评估提供了新的思路。

（2）振荡燃烧。振荡燃烧指发动机在工作时燃烧室产生大幅度压力脉动的非稳定燃烧现象。振荡燃烧对燃烧室结构会产生严重损害[77]。刘帅等[78]采用欧拉方程和基元反应模型对振荡燃烧现象展开数值模拟研究，研究表明振荡燃烧存在频率突变现象，形成低频、高频和超高频的3 种振荡燃烧模态，超高频模态下的振荡燃烧主频为高频模态下的2 倍、低频模态下的5 倍，且在2 种模态的过渡期存在双频耦合现象。该研究对于燃烧室振荡燃烧模式分类提供了重要参考；孙培锋等[79-80]利用激光诱导荧光测量技术（Laser-induced Fluorescence）测量振荡燃烧不同相位的火焰结构，计算了贫预混合预蒸发燃烧室（Lean Premixed Pre-evaporative combustion chamber，LPP）瑞丽指数分布，结果表明火焰局部熄灭、火焰重燃以及脱离和重融共同激励燃烧室振荡燃烧现象，在振荡燃烧发生时在燃烧室喷嘴出口喷入2 次燃料可以有效抑制振荡燃烧现象从而实现对振荡燃烧的主动控制。

（3）压气机喘振。压气机喘振将直接影响发动机的工作稳定性，发动机工作发生喘振不采取措施导致喘振严重甚至可以造成系统毁灭性损伤[81]。作为极易发生故障因素，近年来相关学者对此类非规律性振源进行了大量试验与研究工作[82-84]。雷杰等[85]、闫思齐[86]通过某型发动机动态压力传感器测量，建立了一种基于脉动压力变化检测的喘振检测方法，利用进气总压畸变装置诱使发动机产生喘振，采集信号特征参数探究喘振传播规律；在建模与仿真方面，金帅等[87]建立了压气机基于喘振发生因素的故障树，将发动机喘振排故流程模块化，大幅增加了排故效率和准确性；綦蕾等[88]、郭重佳等[89]对典型喘振和失速影响开展了系统的研究，基于整机气动热力学理论对发动机稳定裕度快速估计方法进行了改进，明确了喘振发生的关键诱因，进一步完善了喘振验证对适航领域的技术支撑；张鑫等[90]、王波等[91]以带CDFS 的航空发动机为研究对象，基于PXI 设计喘振信号仿真系统，通过对判喘参数优化有效避免了某型发动机在喘振时存在误判、漏判等问题。总体而言，近年来压气机喘振的预防和抑制技术是非规律性振源研究中的研究热点，大量试验与仿真技术革新使得本领域研究得到了快速的发展。

（4）叶栅尾流激振。在21 世纪初，叶栅尾流、密封气流激振曾一度成为非规律性振源研究中最热门研究方向，在泄露量和耐磨性之间存在技术矛盾，研发先进密封形式对航空发动机等旋转机械的经济性与安全性有着重要意义。相关学者对激振机理进行了深入研究，给出了有效的抑振措施，如加装反预旋装置、周向遮挡、阻尼密封等等[4]。近年来研究人员发现燃机轴流式压气机均匀尾流会使叶片产生周期激振，杨博宇等[92]通过傅里叶变换将周期激振力展开，分析各阶定常激振力对多自由度阻尼振动模型动力学特性稳态响应，该仿真在工程上有一定参考价值，但未给出对应试验验证。在尾流激振试验方面近5年来成果鲜有报道。

此外，对于恶劣工况条件下发生不可预见振动诱因例如吞水[93-94]、撞鸟[95-97]引起的航空发动机工况瞬时变化等问题有相关学者展开研究并取得了一些研究成果，但未见以此为振源对航空发动机振动传递路径开展研究分析。一些无法避免的振动例如飞机着舰动作、过高的机动载荷引起航空发动机振动进而产生的动力学表征研究由于场地和试验条件所限还未见系统的研究报道。

2 振动传递路径分析

振动在发生时会大大降低机械系统的动态精度与工作状态，严重时可能导致事故的发生，因此振动控制成为改善系统性能的重要方面之一。找到振动能量的传递主要路径，通过对这些主要路径进行结构的优化和参数设计，从而实现控制整个机械系统振动传递的目的。因此分析计算隔振系统的传递路径对于控制整机振动具有十分重要的意义[98-100]。近年来，航空发动机振动敏感性总体提高。由于质量偏心问题导致航空发动机转子系统产生不平衡负载导致90%以上的转子系统质量不平衡的根本原因与制造过程中的技术缺陷有关[101-102]。民用发动机设计公司对机组成员和乘客的舒适性问题提出了新的设计挑战，即尽量减少民用飞机发动机的振动[103-104]。相关研究人员积极参与为民航运输飞机提出创新的噪声控制解决方案[103-107]。在航空发动机装配过程中，基于振动和噪声传播分析进行关键点设计和材料选择，明确振动在发动机系统传递特性，积极减少来自航空发动机转子系统的振动能量传播技术非常重要[108]。

目前通过相关试验建立了比较合理的多个传递路径分析方法，例如传统的TPA、快速TPA、高级传递路径分析方法ATPA、工况传递路径分析OTPA、扩展工况传递路径分析OPAX 等方法，这些方法在不同的应用领域中各有利弊，同时在适用方面也有较多不同，针对不同工程问题采用适用的传递路径分析方法。传统TPA、OTPA 和OPAX 方法是现阶段比较普遍的传递路径分析法。本章将对以上3 种传递路径分析方法近年来研究进展与成果进行总结综述。

2.1 传递路径分析（TPA）

传递路径分析（TPA），20世纪末被广泛应用于汽车NVH 领域，后期逐渐应用到飞机[109]、地铁[110-111]、汽车[112-113]发动机振动传递分析中。TPA 有着明显的优势和缺点。传统TPA 概念简单清晰，计算结果精度高，缺点是工作周期长，需要在动力装置拆除后测量传递函数，参考点选取量大导致需要消耗极大的人力和时间。执行常规振动TPA 分析首先要在非稳态过程中施加载荷等边界条件[114]。其主要思想是将振动系统模型简化，被动端响应为各个传递路径响应叠加，定义为

式中：Ym(ω)为被动端点m的总响应；Hmn(ω)为被动端点m与主动端点n的频响函数；Xn(ω)为主动端点n的载荷。

为了避免拆除动力装置降低传递路径分析效率，近年来相关学者对TPA 算法进行了优化。张磊等[115]提出一种不受振源移除影响的逆矩阵算法，该方法可以在不拆卸动力装置的前提下实现振动源识别。逆子结构TPA 如图9 所示。在此基础上，邓支强等[116]、李宁等[117]引入逆子结构法实现振源耦合，简化了测试流程，提高了分析精度;徐铁等[118]、马俊等[119]提出了一种结构频响函数计算方法，该方法将频响函数广义预测与实际情况相结合，对某款SUV 型乘用汽车进行贡献度分析，获得了频响函数，与OPAX 方法作对比扩展了TPA算法在骑车NVH系统中的应用。

图9 逆子结构TPA

兰靛靛等[120]提出一种高级传递路径分析方法（ATPA），建立车内噪声模型进行工况响应分析，在避免拆卸振源的基础上无需进行载荷识别，直接可以计算频响函数，进一步提高了测试效率;范朝梦等[121]、姜旭东等[122]分别基于有限元仿真及试验对轻型客车和动车组进行了振动贡献度分析，通过优化振动主要贡献路径处的橡胶刚度值改善了车内的振动水平，充分说明了算法的可行性和实用性；杨星瑶等[123]提出了一套完整的振动贡献度计算模拟方法，将NI Compact RIO 作为控制核心，测量缸压信号和机体振动信号，实现对发动机振动贡献度测试的模拟过程，采集信号数据良好，提高了分析的精度。截至目前TPA算法技术已经十分成熟，发展出众多分支，在农业机械和交通领域有诸多应用。

2.2 工况传递路径分析（OTPA）

工况传递路径分析（OTPA），在方法上直接弥补了传统TPA 的短板，传统TPA 基于力矩阵连接振源与响应端矩阵，即力-响应函数传递矩阵，而OTPA 是基于振源与响应端矩阵，即响应-响应函数传递矩阵，计算方便快捷，只需采集运行工况下数据，避免反复拆卸动力源，极大地提高了工作效率。另一方面各个振动传递路径相互作用，存在较强的信号耦合，这种耦合会导致传递路径振动贡献度产生一定误差，很难得到准确的计算结果，但在整体振动贡献度大小分析上并不影响对系统振动关键结构的判别，尤其是提高了计算效率，在交通[124-126]、农业机械[127-128]中仍有广泛的应用。对于任意线性系统传递函数为

式中：x(jω)为系统的输入向量；y(jω)为系统的输出向量；H(jω)为振动系统的传递函数矩阵；jω表示在频域。

OPTA 方法机理较为简单，发动机隔振系统整机OTPA模型如图10所示。

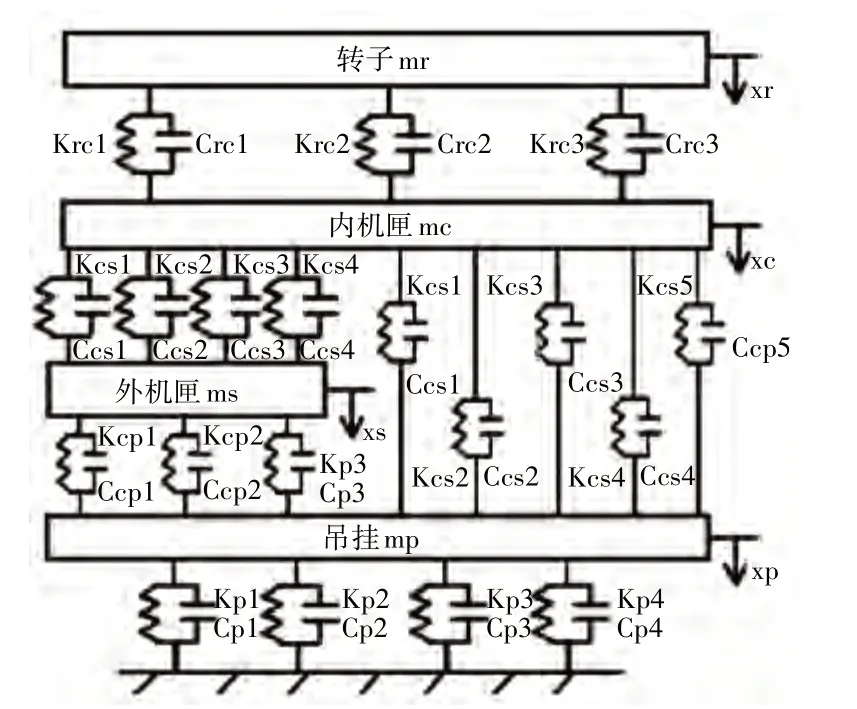
图10 发动机隔振系统整机OTPA模型

其各系统振动微分方程为

（1）转子系统振动微分方程

（2）内机匣系统振动微分方程

（3）外机匣系统振动微分方程

（4）吊挂系统振动微分方程

发动机整机隔振系统质量矩阵为

刚度矩阵为

保留路径1，系统稳态响应为

4自由度隔振系统振动方程为

其稳态响应为

其速度和加速度响应为

针对上述计算未考虑系统信号耦合，李春楠等[129]通过最小二乘法等方法拟合信号奇异值，计算不同路径振动贡献度，分析了贡献度较大的影响因素，为载体降噪指明了优化方向；伍先俊等[130]提出一种可以消除传感器间信息串扰影响的工况传递路径分析方法，采用两声源仿真与试验分析了传感器排布数量对振动传递测试结果的影响，提高了振动预测精度。鉴于OTPA 方法的简单实用性，近年来此方法更是被广泛应用于不同领域载体振动分析中以优化载体振动贡献模式。在汽车振动抑制领域，房旭[131]基于OTPA 对行驶汽车车内噪声声源进行识别，建立了含路面、轮胎等36 条多输入、单输出的振动传递模型；在地铁降噪工程领域，聂嘉兴[132]以地铁为研究对象，基于OTPA 对地铁1 系、2 系传递路径贡献度进行计算和分析，建立三输入单输出的振源串扰模型，采用频响函数矩阵串扰消除方法，开展串扰消除试验，为后续OTPA 分析中消除串扰方法提供指导方向；在船舶工程领域，吴为[133]采用多级OTPA 对船舰复杂振动噪声进行分析，与文献[124]方法类似，通过奇异值分解降低病态矩阵对计算结果造成的影响，基于独立分量分离耦合信号，解决耦合信号对噪声传递产生的结果偏差问题；在农用机械设计领域，陈小亮[134]将工况传递路径分析方法采用奇异值分解法进行改进，建立谷物收割机发动机—驾驶室振动传递模型，利用改进OTPA 进行振动贡献度分析，找到发动机振动对座椅影响贡献度最大路径，优化关键点刚度参数，为提高农用收割机驾驶舒适性提供参考。在贡献度相关的定性分析中，OTPA 方法便捷程度优于传统TPA 方法和OPAX 方法，可以节省大量时间，提高效率，适用领域也更加广泛。

2.3 扩展工况传递路径分析（OPAX）

扩展工况传递路径分析（OPAX）法中传递函数测量方法与TPA 类似，由于不需要大量测点，该方法在工作量上完胜于传统TPA 方法。OPAX 激励与响应关系为

式中：Hki(ω)为载荷到响应端传递函数；Hqi(ω)为载荷到激励端传递函数；uq(ω)为第q个激励端总响应；yi(ω)为第k个接收端总响应；aαi(ω)为第i个连接激励端响应；api(ω)为第i个连接接收端响应；Fi(ω)为第i个连接处载荷。

2012 年，宋海生[135]在博士学位论文中首次将OPAX 与轻型客车NVH 问题结合研究，形成了1 套基于OPAX 的可解决整车NVH 异常问题的理论方法。论文中详细介绍了OPAX相比于传统TPA和OTPA在建模和计算中的优越性，引入条件数理论和决定系数理论，对OPAX 方法进一步完善，至此OPAX 方法正式被用于振动贡献度分析之中。近年来相关学者对OPAX 计算方法不断优化。莫愁等[136]提出逆子结构技术提高OPAX 精度，主要工作为基于逆子结构技术计算系统动刚度、基于小波降噪技术去除系统内噪声干扰；高彬彬[137]、杜充[138]先后以某型乘用车为研究对象，利用LMS 测试平台测量系统频响函数，基于OPAX 方法建立结构振动传递路径模型，根据车内噪声贡献量识别主要振源；陈剑等[139]采用OPAX 方法对某型卡车驾驶室振动传递路径进行分析，提出一种改进的模型建模方法，更准确地反映了振动传递模式，振动贡献最大路径贡献量更加突出，对OPAX 方法工程应用具有很大的参考价值与意义；张俊红等[140]针对信号采集中干扰噪声对原始数据影响的问题，提出一种结合自适应变分模态分解和巴氏距离优化的OPAX 方法，采用粒子群算法对信号进行变分模态分解，实现有效降噪，优化了OPAX 的计算过程，提高了OPAX方法的分析精度。综上，OPAX方法主要适用于汽车NVH领域分析，在航空、海事领域应用鲜有报道。

3 总结与展望

（1）国内外学者针对航空发动机规律性振源展开了系统的研究，随着计算机技术的发展，计算模型的规模逐渐庞大，可考虑因素也越发接近于实际工况，对航空发动机整机振动溯源和分析的指导意义越来越大，但针对非规律性振源故障研究有待加强。航空发动机工况恶劣，部件极易产生脱落磨损，机械松动引发发动机故障十分常见。发动机整机系统支点多、工况温差大且要求安装条件极为严格，稍有偏差便会引起发动机运行过程中产生振动，机械振动的随机性和不可预见性时刻威胁着驾驶员的生命安全，叶栅尾流激振等非规律性振源故障近3 年来也未见报道，这些问题都需要进一步研究.

（2）传递路径分析方法在实际应用中衍生出了很多适合于不同工况下的方法，此类方法被广泛应用于汽车、地铁、船舶领域，但是在航空发动机整机振动传递路径研究还未系统开展。关于发动机故障振源在传递路径上传递响应研究鲜有报道，在航空领域仅有数篇硕、博学位论文基于OTPA 法对民用发动机整机振动贡献度展开分析，OTPA 法信号耦合导致结果不精确的问题还有待解决，同时也未见学者在航空领域应用TPA 法和OPAX 法开展发动机相关试车试验，后续研究可将此类方法引入航空发动机振动分析中。

（3）国内外学者对于航空发动机振动故障类型分析较为全面，但在整机振动传递路径建模研究中对模型简化问题考虑不足。现有文献未将故障参数引入模型当中，计算模型过于理想化，大多忽略系统自身阻尼进行计算分析，发动机在实际工作中其他振动因素并未考虑，对于复杂振动计算手段还不够成熟，有许多工作仍需深入开展。