不相称分数阶Genesio-Tesi系统的有限时间自适应滑模同步

周卫光, 章 安, 郑永爱

(扬州大学信息工程学院, 江苏 扬州 225127)

近年来, 分数阶混沌系统的同步控制因在保密通信、生物科学和社会科学等领域应用前景广泛而成为研究热点. 线性反馈控制[1]、模糊脉冲控制[2]和自适应控制[3-4]等同步控制方案都是渐近实现分数阶混沌系统的同步. 然而, 渐近同步理论耗费的时间趋于无穷大,故有限时间同步更具实际意义. Hui等[5]通过设计与延迟无关的反馈控制器和间歇控制器, 分别实现了具有时变时滞的分数阶记忆神经网络的有限时间同步; Zhang等[6]设计了分数阶有限时间脉冲控制器, 实现分数阶双向联想记忆神经网络的有限时间脉冲同步. 由于滑模控制对不确定参数具有不变性和鲁棒性, 故分数阶混沌系统同步的滑模控制方法被相继提出. Wang等[7]利用深度学习递归神经网络逼近未知扰动, 并结合终端滑模控制设计自适应终端滑模控制器, 实现了分数阶混沌金融系统的有限时间同步; Khan等[8]设计了一种自适应滑模控制器, 实现具有不确定性和外部干扰的分数阶复混沌系统的同步; Modiri等[9]采用含分数阶滑模面的终端滑模控制器, 实现了具有参数不确定性和外部扰动的两个不同混沌系统的有限时间同步.

Genesio-Tesi系统[10-12]是物理学中典型的混沌系统, 具有结构简单和电路易于实现等优点, 被广泛用于保密通讯领域. Tran等[13]提出一种齐次高阶滑模控制方法, 实现了受干扰的Genesio-Tesi系统的有限时间同步; Ghamati等[14]通过设计自适应滑模控制器, 实现具有未知参数和外部扰动的Genesio-Tesi系统的同步; 宋晓娜等[15]采用反步法和滑模控制相结合的策略设计了反步滑模控制器, 实现不确定分数阶Genesio-Tesi系统的全局渐近同步; Khan等[16]利用分数阶扰动观测器对分数阶Genesio-Tesi系统存在的外部未知有界扰动进行估计, 并通过设计自适应滑模控制器实现了分数阶Genesio-Tesi系统的有界投影同步. 本文拟针对含有未知扰动和不确定项的不相称分数阶Genesio-Tesi系统,设计一种新的分数阶有限时间扰动观测器估计系统中存在的扰动和不确定项, 使得扰动误差在有限时间内收敛至零, 并基于该扰动观测器构建合适的分数阶滑模面和有限时间自适应滑模同步控制器, 以期实现系统的有限时间同步.

1 预备知识

定义1[17]Caputo 分数阶导数

(1)

引理1[18]设x(t)∈R是一个连续可导的函数, 则对于任意的t≥t0且0≤q≤1,有

(2)

引理2[19]设

(3)

其中y1(t)∈Rn和y2(t)∈Rn具有连续一阶导数,Q1∈Rn×n和Q2∈Rn×n为两个正定矩阵.若存在正定矩阵Q3∈Rn×n和常数h0>0, 使得

(4)

则‖y1(t)‖和‖y2(t)‖有界且y1(t)渐近趋于零, 即limt→+∞‖y1(t)‖=0.

引理3假设函数V(t):[0,+∞)→R+∪{0}是连续的, 如果存在常数00, 0<ρ<1使得

(5)

2 系统描述

考虑分数阶Genesio-Tesi系统

(6)

其中x1,x2,x3为状态变量,分数阶q1,q2,q3∈(0,1),a,b,c为系统参数.

以系统(6)为驱动系统, 相应的具有外部扰动和不确定项的响应系统为

(7)

其中y1,y2,y3为状态变量,d(t)为外部扰动, Δf(y)为不确定项,q1,q2,q3∈(0,1),ui(t)为控制输入,i=1,2,3.

定义误差变量ei=yi-xi,i=1,2,3,可得误差系统为

(8)

对于不同的初始值x(0),y(0),若存在一个常数t1满足limt→t1|ei(t)|=0, 以及当t>t1时有|ei(t)|=0,i=1,2,3, 则驱动系统(6)与响应系统(7)可实现有限时间同步.

3 主要结果

3.1 分数阶有限时间扰动观测器的设计

为了处理响应系统(7)中外部扰动d(t)和不确定项Δf(y), 定义总扰动为M=d(t)+Δf(y).

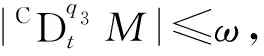
(9)

其中z(t)为辅助变量,满足

(10)

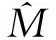
(11)

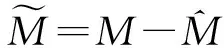
证明 将响应系统(7)与式(10)代入扰动观测器(9), 可得

(12)

结合假设1, 将式(11)代入式(12)可得

根据引理3, 收敛时间

3.2 有限时间自适应滑模同步控制器的设计

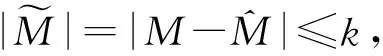
(13)

其中0<η<1.设计如下控制器:

u1(t)=-λ1|e1(t)|ηsgne1(t),

(14)

u2(t)=-λ2|e2(t)|ηsgne2(t),

(15)

(16)

其中σ1>0,σ2>0,ω>0.自适应律为

(17)

定理2在假设1～2的条件下, 若设计分数阶扰动观测器(9)和自适应滑模控制器(14)～(17), 则误差系统(8)的轨迹在有限时间内到达滑模面且闭环系统中所有信号都是有界的.进一步地, 误差系统(8)的零点是有限时间稳定的, 即驱动系统(6)与响应系统(7)实现有限时间同步.

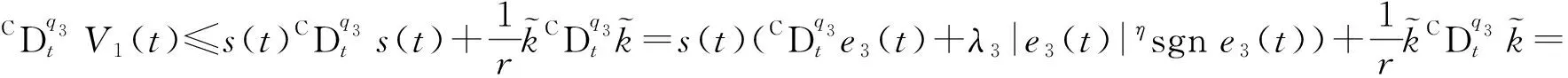
向其中代入控制器(16)和自适应律(17),可得

根据引理2, 误差系统(8)的轨迹渐近到达滑模面且闭环系统中所有信号都是有界的.

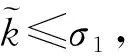
故误差系统的状态轨迹可以在有限时间内到达滑模面.

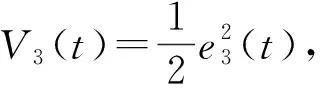
根据引理3, 收敛时间为

其中0<η<1.故e3(t)在有限时间内收敛到零, 即误差系统状态e3(t)的轨迹到达滑模面后可以在有限时间内收敛至原点.

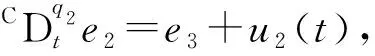
4 数值仿真

当q1=0.93,q2=0.95,q3=0.99,a=1.2,b=2.92,c=6时, 设定初始条件为x(0)=[1,-2,3]T, 分数阶Genesio-Tesi系统(6)呈混沌现象, 该系统的混沌吸引子如图1所示.

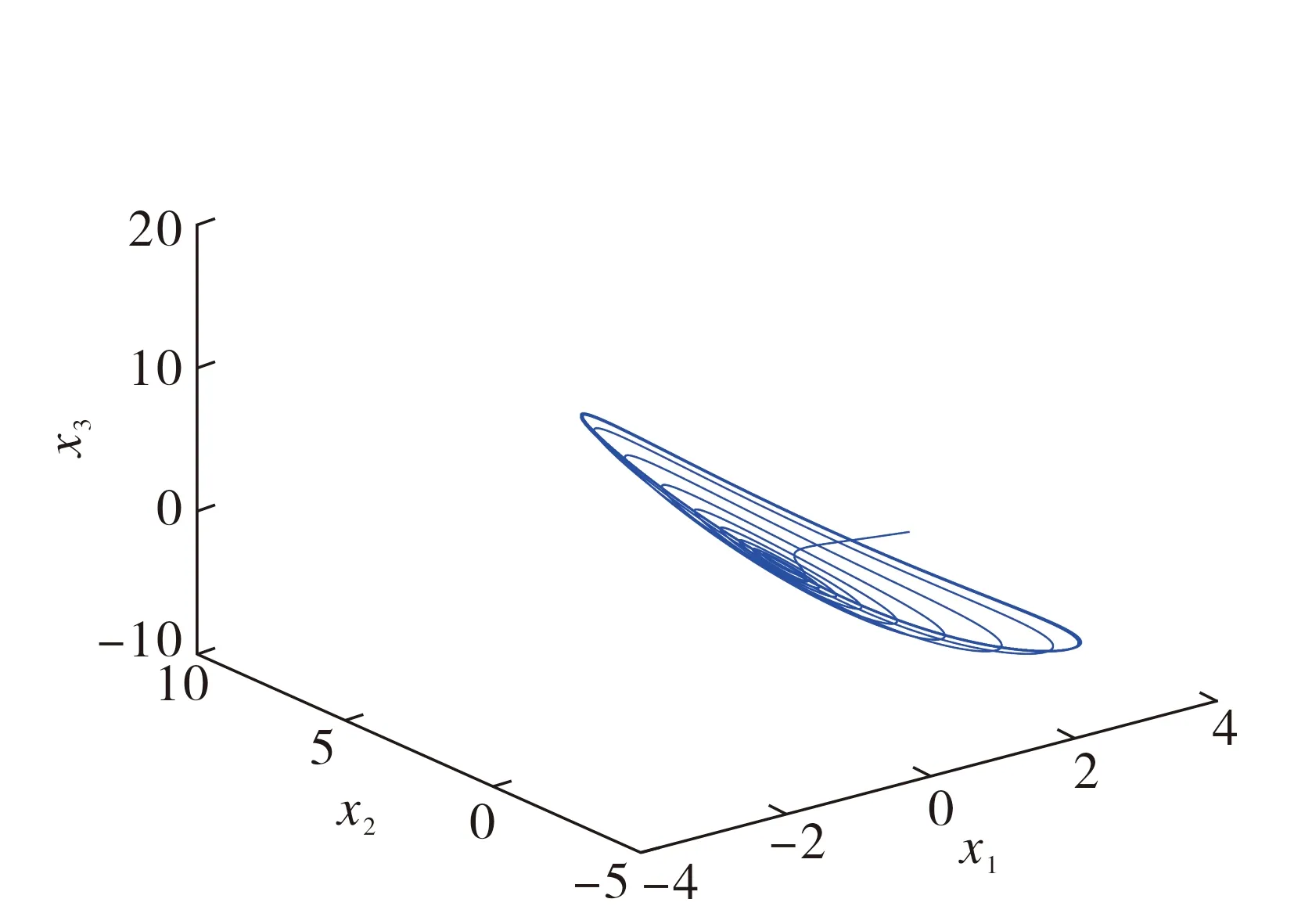
图1 分数阶Genesio-Tesi混沌系统吸引子Fig.1 Attractor of fractional order Genesio-Tesi chaotic system

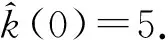
图2 总扰动M和扰动估计的轨迹Fig.2 The trajectory of total disturbance M and disturbance estimation

图3 估计误差的轨迹Fig.3 Trace of estimation error

在自适应滑模控制器(14)～(17)下, 驱动系统(6)、响应系统(7)以及同步误差系统(8)的状态响应轨迹如图4～5所示, 自适应律估计曲线如图6所示.由图4～5可知, 在有限时间内驱动系统(6)和响应系统(7)的运动轨迹趋于一致, 误差系统(8)在有限时间内收敛到零, 即驱动系统(6)与响应系统(7)实现有限时间同步.由图6可知, 未知正常数k也收敛于某一常数值.

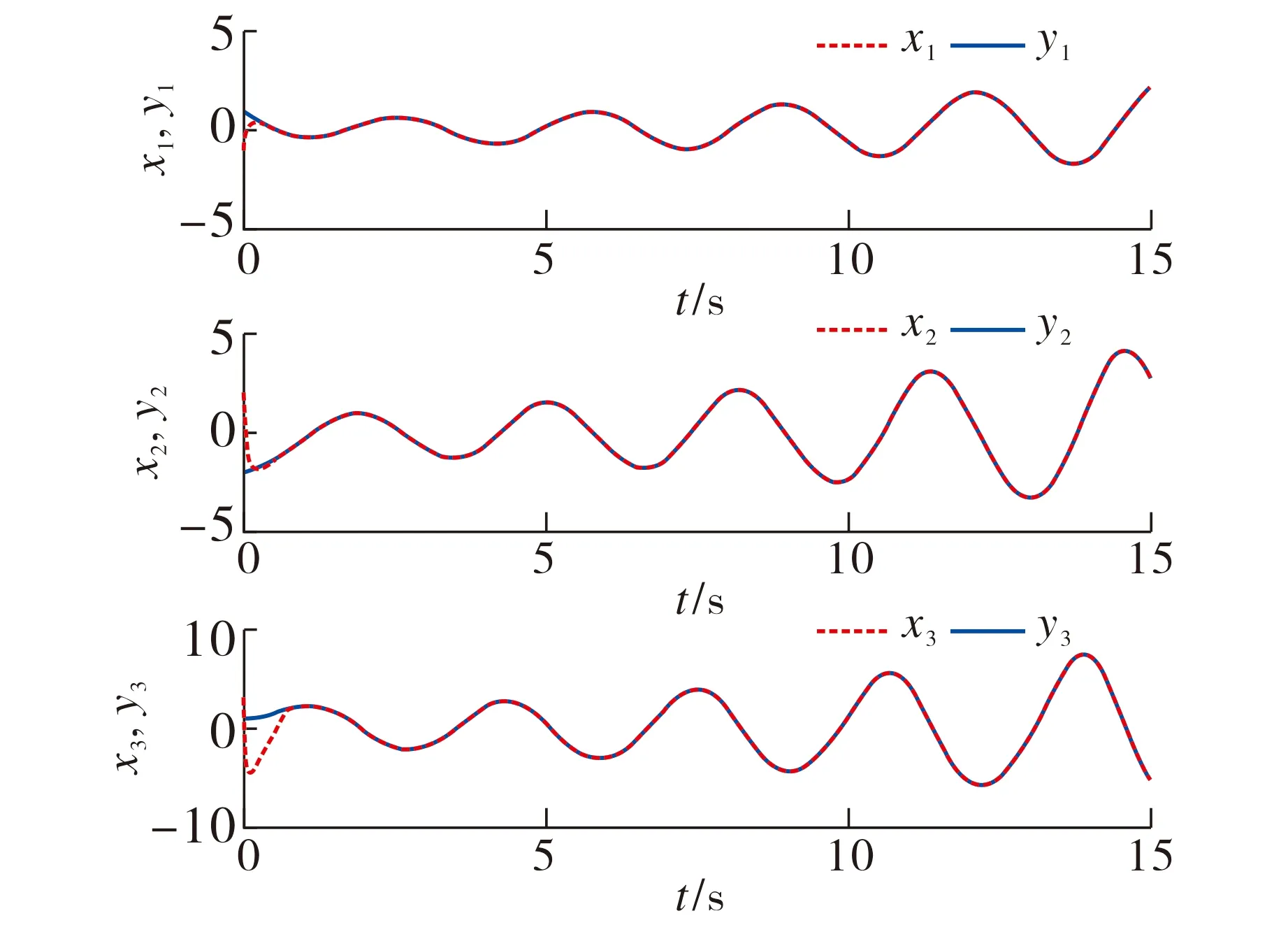
图4 驱动系统(6)与响应系统(7)的状态轨迹Fig.4 State trajectory of drive system (6) and response system (7)

图5 同步误差的轨迹Fig.5 The trajectory of synchronization error

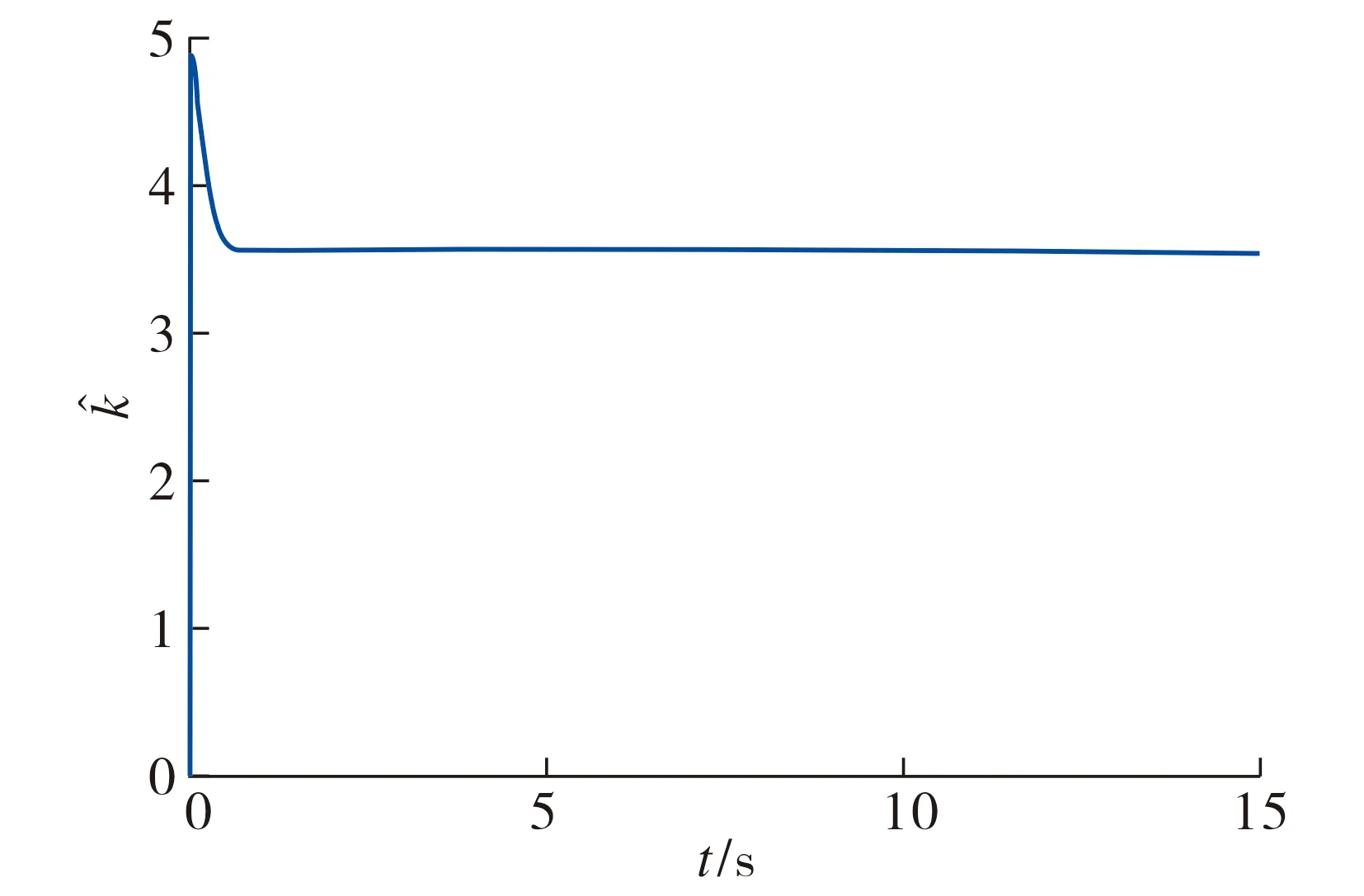
图6 k的估计曲线Fig.6 Estimation curve of k

5 结论

本文选择含有未知扰动和不确定项的分数阶Genesio-Tesi混沌系统作为研究对象, 利用分数阶有限时间同步理论, 设计有限时间扰动观测器对该系统中的未知扰动和不确定项进行估计. 基于分数阶Lyapunov理论和自适应控制理论, 设计合适的有限时间自适应滑模控制器, 实现了含有未知扰动和不确定项的分数阶Genesio-Tesi混沌系统的有限时间同步. 本文所提方法可为混沌系统的同步控制问题及相关研究提供参考.