转轮虫种群对培养基氮磷含量的响应及动力学特征

冯婷婷, 项贤领, 朱 敏

(1. 安徽师范大学 a. 数学与统计学院; b. 生态与环境学院, 安徽 芜湖 241002;

近年来, 随着全球气候变暖及工业化的快速发展, 富含氮磷的生活污水和工业废水的排放以及农田氮磷肥的流失导致水体富营养化日趋严峻, 已成为我国当前乃至今后相当长一段时期内的重大水环境问题[1]．氮、磷等元素是藻类生长和繁殖所必需的营养元素, 也是大多数水生和陆地生态系统的主要限制因子[2]．然而, 氮和磷在控制湖泊富营养化中的作用也存在较大争议, 有学者认为淡水中磷是主要限制因子, 海水中氮则是主要限制因子, 而在河口栖息地可能是过渡性的[3]; 也有学者认为仅控制磷就足以控制富营养化, 生物固氮可以最终补偿浮游植物群落中氮的缺乏, 因而磷是其生长的主要限制因子[4-5]; 还有学者则认为氮元素对湖泊富营养化也起着重要的作用[6-7]．因为水中营养物质的化学计量比可以影响浮游生物的生长和组成[8-9], 越来越多的学者认为氮磷比(N/P)可以作为评价营养盐对藻类生长限制水平的一个指标, 所以在解决湖泊富营养化问题时, 须同时控制氮和磷．Redfield等[10]认为藻细胞组成的临界元素比为C∶N∶P=106∶16∶1, 故若氮磷比超过16∶1, 则磷元素通常被认为是限制性因素; 若氮磷比小于10∶1, 则氮元素成为限制性因素; 而当氮磷比在10～20时, 氮或磷成为限制性因素则变得不确定[11-13]．目前, 氮磷比学说已广泛应用于解释藻类优势种群形成的机理, Schindler[14]认为低氮磷比有利于蓝藻在水体中形成优势; Smith[15]则指出可通过管理措施改变湖泊水体的氮磷比来减少藻类水华的发生．因此, 在水生生态系统中, 氮磷比常作为预测藻细胞密度变化和季节演替的关键因子[16]．水体中氮磷等营养元素不足时, 藻类在浓度和质量上的变化可引起浮游动物的高死亡率和种群密度的下降[17-18], 而轮虫等小型浮游动物则可通过将生长和产卵量降至最低的生活史对策来耐受食物的匮乏[19]．因此, 研究小型浮游动物的生活史特征对解释植食性浮游动物间对环境资源的竞争有着重要意义．关于轮虫对水体的氮磷含量及藻类的响应和适应性研究已有大量报道[20-21], 然而, 在不同氮磷配比条件下培养的藻类对其摄食者轮虫种群的影响尚不可知, 在何种资源配比下可实现捕食者轮虫的最大增长潜力仍有待进一步研究．

种群动力学模型能揭示种群与种群、种群与其生境间相互作用的动力学关系,该模型可用来描述、预测甚至调控自然界物种的发展过程与趋势。 在被捕食者-捕食者系统中随着营养物质供应的不断增加, 种群密度波动幅度逐渐增大, 系统的稳定性降低, 最终导致系统内的物种灭亡[22]．研究种群模型的稳定性和分岔性质, 不仅可以得到系统解随时间变化的性态,还可以得到系统受外界干扰时系统解的性态变化, 从而得到种群的演化规律, 这对于预测种群在未来的发展状况并采取相应的措施具有广泛的理论意义[23]．斜生栅藻(Scenedesmusobliquus)是淡水中极为常见的绿藻, 可以在营养丰富的静水中快速生长繁殖, 也是许多水产动物育苗的生物饵料和浮游动物的食物．本文拟通过在不同氮磷配比下培养斜生栅藻, 并以此作为牧食者转轮虫(Rotariarotatoria)的食物, 从而观测不同氮磷配比培养基对转轮虫的摄食行为及种群繁殖与存活状况的影响, 并运用Malthus模型分析培养基氮磷配比对本实验系统的影响, 探明可实现捕食者转轮虫最大增长潜力的条件, 为深入理解营养元素输入配比对生态系统生产力的影响及生态系统稳定性提供理论依据．

1 材料与方法

1.1 转轮虫的采集和培养

实验中所使用的转轮虫均采自安徽省和县敬庄村(31°73′67″ N, 118°33′72″ E)附近的池塘中, 并在28 ℃恒温光照培养箱中单克隆培养．光照度和光暗比(L/D)分别为130 lx和14 h∶10 h, 保种培养时间为6个月以上, 培养液为新配置的EPA培养液[24](pH=7.4～7.8), 饵料为斜生栅藻, 投喂密度为1.0×106cells·mL-1．

1.2 斜生栅藻的培养和元素分析

斜生栅藻购自中国科学院水生生物研究所淡水藻种库．不同氮磷比培养基的配制以BG-11培养基为基础, 在500 mL锥形瓶中先配置无氮无磷培养基, 再分别以K2HPO4和NaNO3(购自上海生工生物工程股份有限公司)为磷源和氮源, 基于5 mg·L-1的氮元素质量浓度和0.2 mg·L-1的磷元素质量浓度并按照氮磷比(N/P)分别为5, 16和30的比例配制6组培养基, 具体浓度见表1．在该培养基中接入经漂洗和饥饿处理后的藻种, 接种密度为2×105cells·mL-1, 置于恒温光照培养箱中(28 ℃, 3000 lx, L/D 为12 h∶12 h)进行半连续培养, 每天人工摇藻3次．收集处于对数生长期的斜生栅藻, 离心计数后置于4 ℃冰箱中保存．

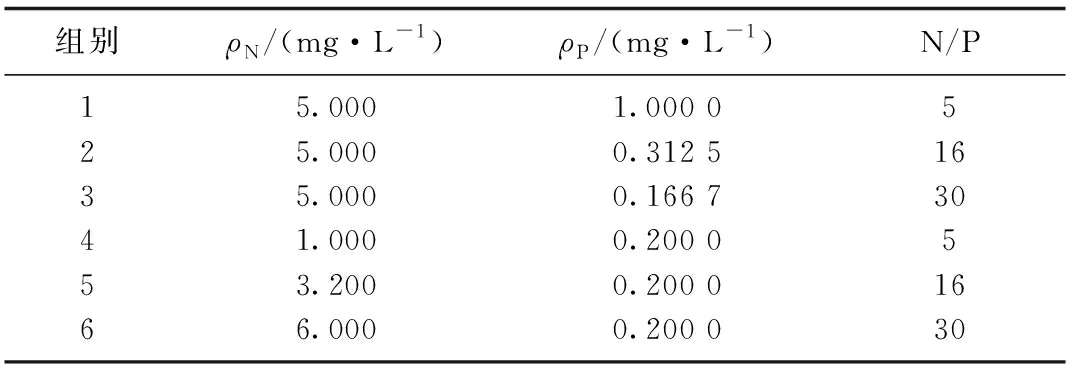
表1 不同组别斜生栅藻培养基中N, P质量浓度及氮磷比Tab.1 The concentrations and ratios of nitrogen and phosphorous in different medium groups for Scenedesmus obliquus

为检测藻细胞中碳氮磷元素的含量, 取部分离心藻细胞于30 ℃烘箱中干燥24 h, 采用德国Elementar公司的vario MICRO cube元素分析仪检测碳氮含量, 美国Thermo Scientific公司的iCAP7400电感耦合等离子体原子发射光谱仪检测磷元素含量．

1.3 转轮虫的摄食实验

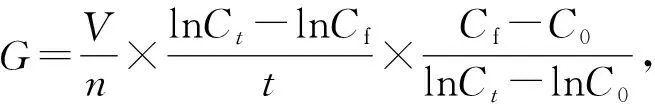
1.4 转轮虫生命表实验

实验开始时, 从预培养的转轮虫种群中挑选约1 000只生长状况良好的成熟母体, 从其后代中随机吸取48只龄长小于6 h的转轮虫幼体, 分别转移到每孔含0.5 mL EPA培养液的2个24孔培养板中, 并以上述不同氮磷配比下培养获得的藻细胞为食, 喂食密度为1.0×106cells·mL-1．每个组别2个培养板, 共12个培养板, 置于光照培养箱中培养(28 ℃, 130 lx, L/D为14 h∶10 h)．每12 h检查一次, 记录下每只起始个体产下的幼体数量,并将幼体从凹孔中弃除, 每24 h更换新鲜培养液和食物, 通过记录转轮虫在不同处理组下的存活情况和幼体产量, 计算出转轮虫的繁殖率r和死亡率m．实验进行至第41天全部转轮虫个体死亡时结束．

1.5 数据分析与处理

采用单样本Kolmogorov-Smirnov方法和Levene’s test进行数据的正态分布和方差齐性检验．采用单因素方差分析法,通过多重比较(SNK-q检验)分析不同组别下斜生栅藻细胞内碳氮磷元素的含量差异, 分析转轮虫的摄食率和培养基组别之间的关系, 检验不同氮磷配比培养的斜生栅藻对转轮虫存活率和繁殖率的影响．

对获得的实验数据进行处理, 并基于转轮虫的摄食率G、繁殖率r和死亡率m与氮磷配比的关系建立转轮虫种群增长数学模型, 分析获得可实现捕食者转轮虫最大增长潜力的最佳氮磷浓度．

2 结果与分析

2.1 藻细胞的元素含量

图1为不同氮磷比培养的斜生栅藻细胞内C,N,P含量及元素比值．从图1可以看出, 随着氮磷比的升高, 藻细胞的N/P呈升高趋势．在第1,2,4,5组的藻细胞内N/P小于10∶1, 而第3,6组大于10∶1, 介于10～20之间．在ρN=5.000 mg·L-1的3个实验组(第1～3组)中, 藻细胞中的C/N,C/P和N/P逐渐增加, 尤其是第3组的比值增长最显著, 但N和P含量却逐渐减少．在ρP=0.200 0 mg·L-1的3个实验组(第4～6组)中, 藻细胞中的C/P和N/P逐渐增加, 而C/N递减, N含量递增, C和P含量则在第5组中最高．

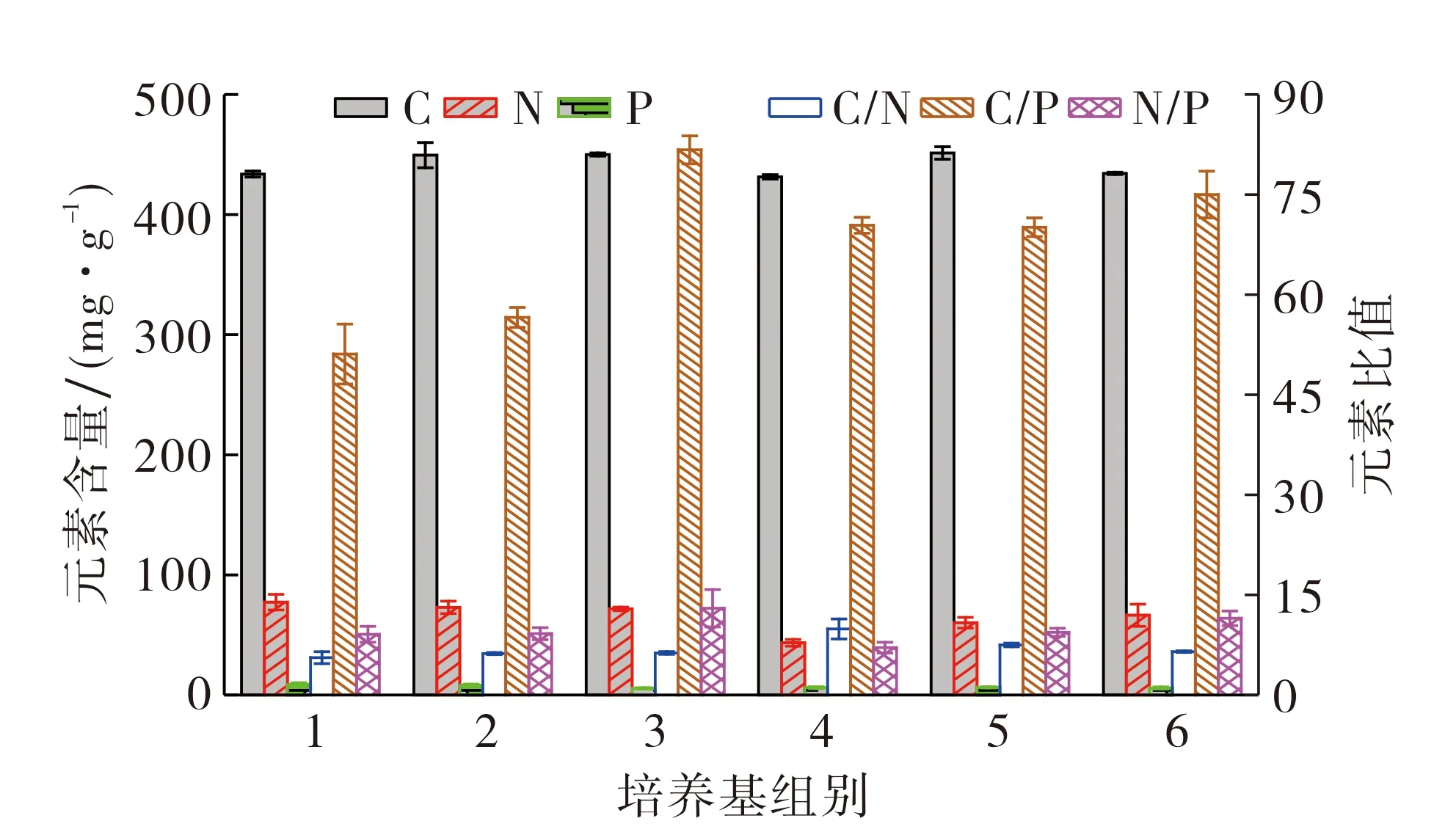
图1 不同氮磷比培养的斜生栅藻细胞内C,N,P含量及元素比值Fig.1 The C, N and P content and their ratios in S. obliquus cells cultured in different N/P ratios medium

2.2 不同藻类喂食下转轮虫的摄食率、存活率和繁殖率

表2为不同藻类组别喂食下转轮虫的摄食率G、繁殖率r和死亡率m．表2结果显示, 通过One-way ANOVA和多重比较分析发现, 不同氮磷比培养的斜生栅藻对转轮虫摄食率仅在第4组(N/P=5)显著高于第6组(N/P=30), 而其余各实验组间无显著影响(P>0.05); 转轮虫的繁殖率在第3组和第6组中显著高于其他4组, 而其他4组间则无显著差异; 转轮虫死亡率在第5组中最高, 第4组中最低, 其余各组间无显著差异．结合元素含量分析结果不难发现, 摄食高氮磷比培养基中藻类的转轮虫拥有较高的繁殖率; 而当培养基中氮磷浓度较低且氮磷比也最低时, 转轮虫为获取更多营养,被迫提高摄食率,使其死亡率大幅下降．因此,水体中氮磷比能显著影响斜生栅藻的生长及质量,表明藻类水华的生长对水体中氮磷比具有较强的依赖性,从而进一步制约了捕食者的繁殖率、摄食率和死亡率．

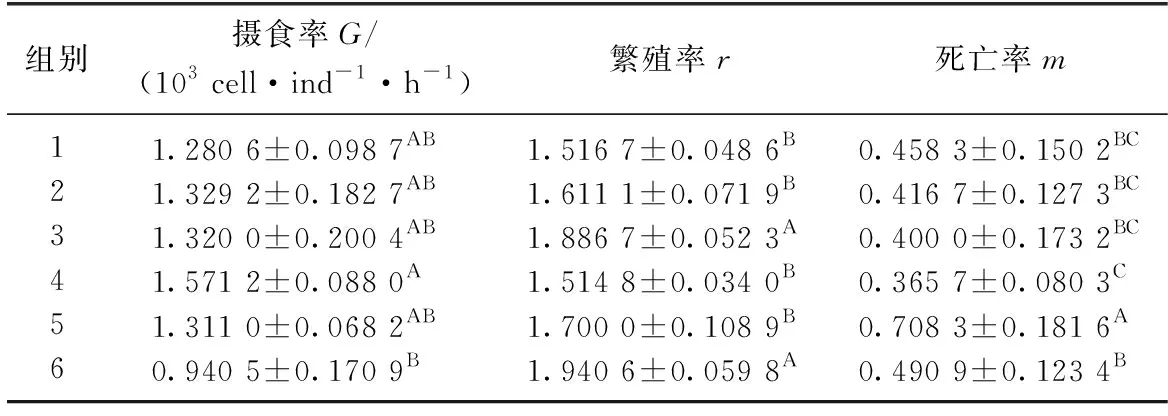
表2 不同藻类组别喂食下转轮虫的摄食率G、繁殖率r和死亡率mTab.2 The feeding rate G, reproductive rate r and mortality rate m in different medium groups for rotifer Rotaria rotatoria

2.3 数学模型

2.3.1 模型

根据Malthus种群模型的意义[25], 本文建立转轮虫生长模型为

(1)

其中U(t)为转轮虫在t时刻的种群密度,U0为初始时刻转轮虫的种群密度, 斜生栅藻的初始密度W0=1.0×106cells·mL-1, 能量转换效率e和半饱和常数b分别取为e=0.6和b=0.6[26-27]．由实验结果可知, 转轮虫的摄食率G、繁殖率r和死亡率m都与N, P浓度有关, 故假设这3个参数值均为N, P含量的二次函数, 记为G(ρN,ρP),r(ρN,ρP)和m(ρN,ρP)．利用变量分离及积分方法, 结合初值条件求解微分方程(1), 得

(2)

2.3.2 模型拟合

由Taylor公式, 假设

(3)

r(ρN,ρP)=r0+r1(ρN-ρN0)+r2(ρP-ρP0)+r3(ρN-ρN0)2+r4(ρP-ρP0)2+r5(ρN-ρN0)(ρP-ρP0),

(4)

(5)

为获得与式中G(ρN,ρP),r(ρN,ρP)和m(ρN,ρP)较近似的二次多项式, 须取定(ρN0,ρP0)．采用方差的思想,令

y1=(5-ρN0)2+(5-ρN0)2+(5-ρN0)2+(1-ρN0)2+(3.2-ρN0)2+(6-ρN0)2,

(6)

y2=(1-ρP0)2+(5/16-ρP0)2+(1/6-ρP0)2+(0.2-ρP0)2+(0.2-ρP0)2+(0.2-ρP0)2,

(7)

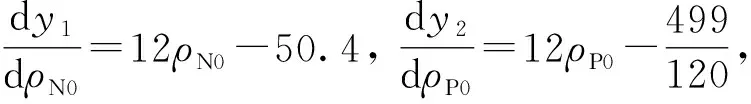
利用实验数据, 并通过MATLAB计算可分别获得gi,ri和mi(i=0, 1, 2, 3, 4, 5)的近似数值, 代入式(3)～(5),得近似函数

(8)

(9)

(10)

将不同组中的氮磷含量以及对应的摄食率、繁殖率和死亡率数据分别带入函数(3)～(5)中, 得到3个六元一次线性方程组, 再通过MATLAB求解线性方程组得到摄食率、繁殖率和死亡率的拟合函数(8)～(10)．该拟合值与实验实测数据完全吻合, 表明拟合函数能较好地表征摄食率G(ρN,ρP)、繁殖率r(ρN,ρP)和死亡率m(ρN,ρP)．

2.3.3 模型分析

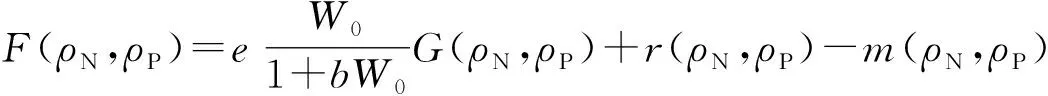
U=U0exp(F(ρN,ρP)t)．

(11)

借鉴可行域中最值的求解方法[28], 对氮磷含量取值范围的可行域进行如下分析．

情形Ⅰ氮磷含量取值范围内情形．F(ρN,ρP)> 0时,F(ρN,ρP)越大,转轮虫的种群密度增长越快;反之,转轮虫的种群密度增长越慢．本文实验设计的氮磷比在5～30之间,且氮磷含量取值范围为1 mg·L-1≤ρN≤6 mg·L-1, 0.166 7 mg·L-1≤ρP≤1 mg·L-1, 即考虑图2中阴影区域内U的最值问题．

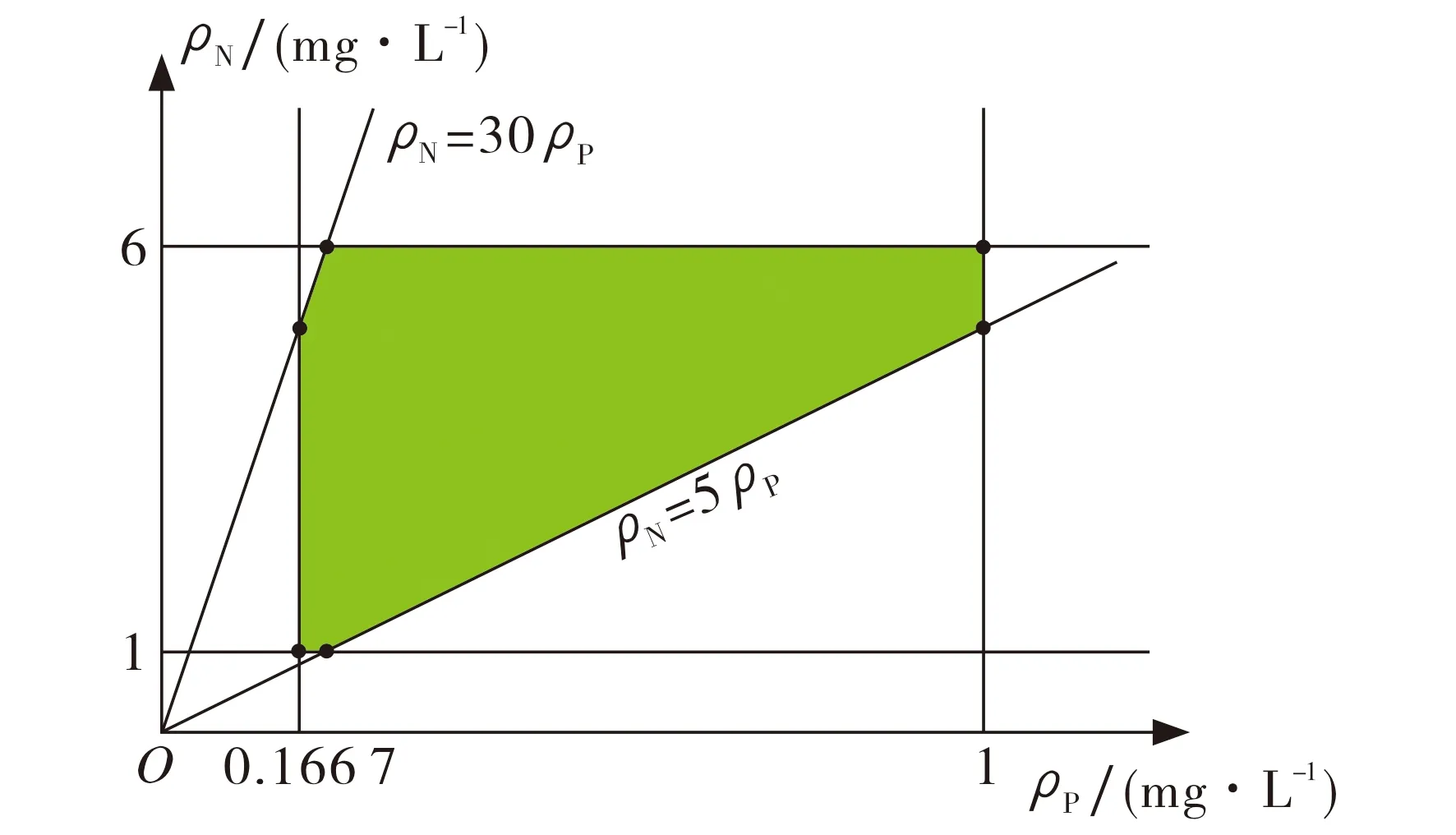
图2 N、P含量及元素比值可行域Fig.2 The N and P content and their ratios feasible region

由MATLAB计算可知,ρN=6.000 0 mg·L-1,ρP=1.000 0 mg·L-1时,F(ρN,ρP)为最大值, 有F(6.000 0, 1.000 0)≈1.228 7×104, 此时转轮虫种群密度增长最快,种群增长模型为U1(t)=U0exp(1.228 7×104t)．而当ρN=1.322 2 mg·L-1,ρP=0.200 0 mg·L-1时,F(ρN,ρP)取最小值, 有F(1.322 2, 0.200 0)≈0.001 0, 此时转轮虫种群密度增长最慢,种群增长模型为U2(t)=U0exp(0.001 0t)．图3给出了这两种情况的动力学模拟图．

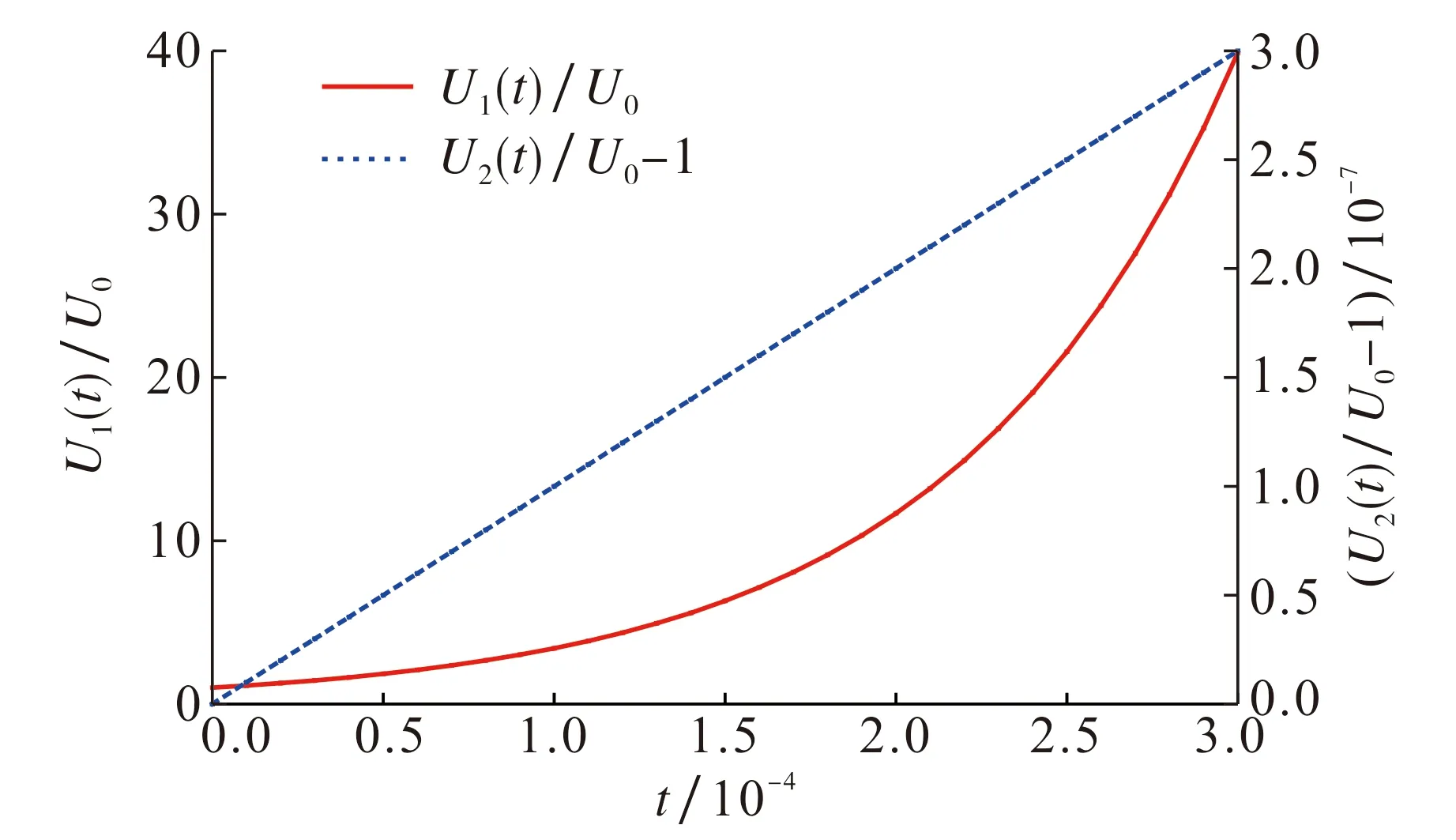
图3 U1(t)和U2(t)动力学模拟图Fig.3 U1(t) and U2(t) dynamic simulation diagram

情形Ⅱ限制性因素不确定情形．当氮磷比为10～20时, 氮亦或是磷成为限制浮游生物生长的因素变得不确定[11-12], 故可在1 mg·L-1≤ρN≤6 mg·L-1, 0.166 7 mg·L-1≤ρP≤1 mg·L-1范围内考虑如图4所示阴影区域内U的最值问题．

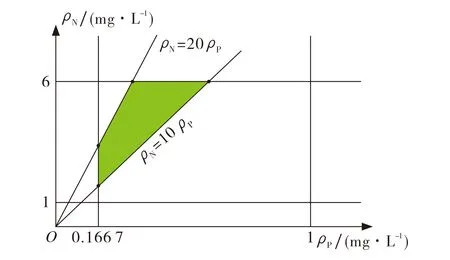
图4 N, P含量及元素比值可行域Fig.4 The N and P content and their ratios feasible region

通过MATLAB计算可知,ρN=6.000 0 mg·L-1,ρP=0.600 0 mg·L-1时,F(ρN,ρP)取最大值6.145 3×103, 此时转轮虫种群密度增长最快, 种群增长模型为U3(t)=U0exp(6.145 3×103t); 当ρN=2.010 5 mg·L-1,ρP=0.200 1 mg·L-1时,F(ρN,ρP)取最小值0.001 0, 此时转轮虫种群密度增长最慢, 种群增长模型为U4(t)=U0exp(0.001 0t)．图5给出了这两种情况的动力学模拟图．

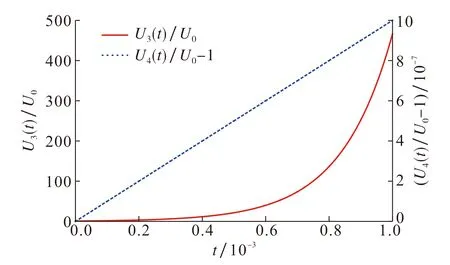
图5 U3(t)和U4(t)动力学模拟图Fig.5 U3(t) and U4(t) dynamic simulation diagram

3 结论

本文模型能够在一定生物学意义下对转轮虫在不同营养条件下的生长状况进行有效分析,对不同营养条件下转轮虫种群动态的预测具有一定的生物学指导意义,在模拟氮磷配比对转轮虫生长的影响方面实现了由“普通定量”向“合适预算”的转变．若将该模型推广至更大范围的水体中, 不仅要考虑更多营养元素对生物种群的影响,在数学建模方面还要兼顾其他物种对实验对象产生的干扰,应考虑更复杂的种群生长模型．