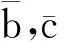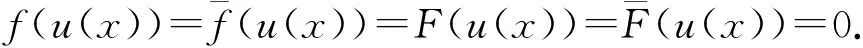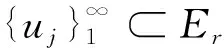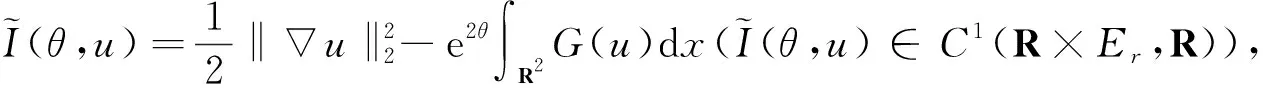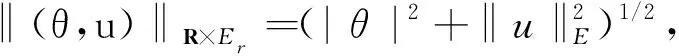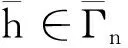平面上一类椭圆问题无穷多解的存在性
刘硕磊, 陆秋平
(扬州大学数学科学学院, 江苏 扬州 225002)
在寻求Schrödinger方程或Klein-Gordon方程某种特定驻波解时须考虑本文所涉及的椭圆问题.当空间维数N≥3及非线性项在零点的增长条件q=1时, Berestycki等[1-2]运用约束极小化的方法分别证明了椭圆问题最低能量解的存在性和无穷多球对称解的存在性; 当N≥3, 0 引理2i) 存在依赖于q的常数C1, 使得对任意的v∈Er, 当|x|≥1时, |v(x)|≤C1|x|-2/(q+3)‖v‖E; ii) 当q+1 -Δu(x)=g(u(x)),x∈R2,u∈E, (1) 定理3若假设(H1)~(H3)成立, 则问题(1)有非负最低能量解以及无穷多个球对称的非平凡解. 为了证明定理3, 需要构造连续函数 椭圆问题 (2) 性质4(ii)即为Ambrosetti-Rabinowitz条件[14], 能保证J(u)的P.S.序列的有界性, 在此基础上, 引理2保证其P.S.序列的紧性.显然, 问题(1)的非线性项并不满足Ambrosetti-Rabinowitz条件. 引理5存在与引理1中C有关的常数ρ1>0, 使得对任意的u∈E满足‖u‖E≤ρ1,有 (3) 式(3)是有界区域上Moser-Trudinger不等式[15]在全平面上经典的简单推广, 类似的推广可参考文献[13].结合有界区域上经典的Moser-Trudinger不等式, 可知本文定义的泛函I(u),J(u)是有意义且连续可微的. ii) 对任意u∈Er,I(u)≥J(u); iii) 存在r0>0及ρ0>0使得I(u),J(u)≥0,‖u‖E 性质6(i)使得式(1)和(2)的解与相应能量泛函的临界点一一对应, 从而将求方程的解转化为寻找泛函的临界点; 性质6 (ii)则保证了能量泛函I(u)可拥有无穷多的临界值, 从而表明方程(1)有无穷多个球对称解; 性质6(iii)和(iv)说明能量泛函I(u),J(u)拥有Mountain pass几何结构, 故可定义I(u),J(u)相应的Mountain pass (minimax)值[5]: bn=infh∈Γnmaxω∈DnI(h(ω)),cn=infh∈Γnmaxω∈DnJ(h(ω)), (4) 以及经典的Mountain pass值[5]: bn≥cn≥ρ0. (5) 由引理1及引理2(i)可知, 对任意的M>0, 存在RM>0使得 当|x|≥RM且‖u‖E≤M时, |u(x)|≤σ0. (6) 结合性质4(i), 得 (7) 引理8[5]i)J(u)的P.S.序列是紧的; ii)cn(n∈N)是J(u)的临界值,cn→∞,n→∞. (8) 且对任意的θ∈R,u∈Er,有 (9) 利用形变引理[16]或Ekeland原理[17]易得: 定理11假设(H1)~(H3)成立, 则bn(n∈N)是I(u)的临界值. 定理3的证明结合定理11和定理12可证.1 预备知识

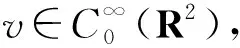
2 主要结果



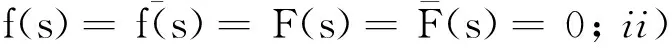
3 定理证明