广义复阶α型Bazilevi函数的一些性质

敖 恩, 李书海

(赤峰学院 a. 数学与计算机科学学院; b. 民族数学教育研究所, 内蒙古 赤峰 024000)

1 预备知识

设函数f(z)和g(z)在单位圆盘D内解析, 若存在一个解析函数φ(z), 使得f(z)/φ(z)在D内解析且|φ(z)|≤1和ω(0)=0, |ω(z)|<1满足f(z)=φ(z)g(ω(z)),则称函数f(z)在D内拟从属于g(z), 记为f(z)qg(z),z∈D．当φ(z)=1时,f(z)=g(ω(z)), 即函数f(z)在D内从属于g(z), 记为f(z)g(z),z∈D．由此易知, 大众所熟悉的从属关系是拟从属关系的特殊情形．

当参数α,γ及函数φ(z),φ(z)取特殊值时,可得以下函数子类．

1) 当α=0时, 得广义复阶星形函数类[10]

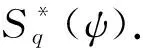
2) 当α=1时, 得广义复阶近于凸函数类

取γ=1,则得广义近于凸函数类

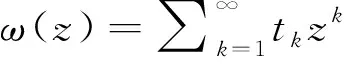
2 主要结果

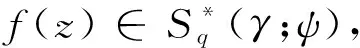
(1)

其中|φ(z)|≤1,ω(z)∈Ω,ψ(z)∈Φ．

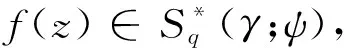
在定理1中, 取γ=1可得下面推论．

定理2设α>0,f(z)∈Bq(α,γ;φ,ψ),则

(2)

其中|φ(z)|≤1, |φ1(z)|≤1,ω(z),ω1(z)∈Ω,φ(z),ψ(z)∈Φ．

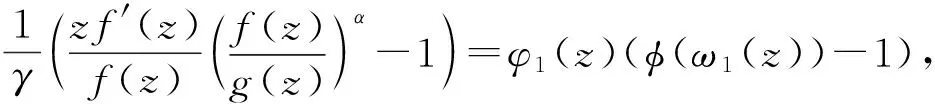
(3)

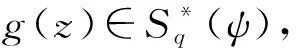
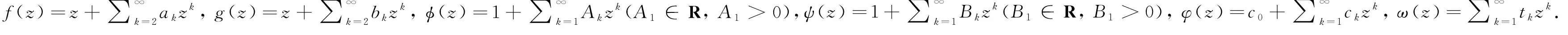
定理3设函数f(z)∈Bq(α,γ;φ,ψ),则

(4)

(5)

且对任何复数μ有

(6)

证明 设函数f(z)∈Bq(α,γ;φ,ψ), 则存在解析函数φ(z)和ω(z): |φ(z)|≤1,ω(0)=0, |ω(z)|<1,使得

(7)

将函数f(z),g(z)的幂级数展开式代入式(7)左侧, 得

(8)

将函数φ(z),φ(z)和ω(z)的幂级数展开式代入式(7)右侧, 得

(9)

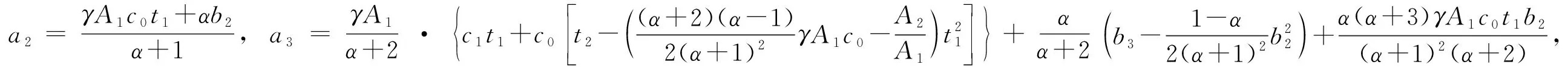
(10)

(11)

在定理3中, 分别取α=0,α=1可得下面推论．

注在定理3中取α=0,γ=1或推论2中取γ=1时, 可得引理3, 即文献[9]中定理2.1．