一类分数阶时滞微分方程解的存在性及稳定性

管重阳, 董琪翔

(扬州大学数学科学学院, 江苏 扬州 225002)

分数阶微积分被认为是经典微积分的推广, 至今已有300多年历史．然而, 早期数学家们对分数阶微分方程的研究基本停留在纯数学理论的基础上．直到近几十年, 分数阶微分方程在理论和应用上才得到了迅速的发展[1-2], 分数阶微积分逐渐从纯数学研究领域渗透到许多科学研究和工程应用中．如今,分数阶微分方程在诸多领域的应用已经取得许多重要成果, 在解的存在性、唯一性等基本理论和方法方面都已有了重要的结论[3-5]．由于时滞是客观世界和工程领域的普遍现象,因此在很多实际系统中, 为了能更准确地描述系统, 需要同时考虑分数阶导数和时滞的影响[6]．Benchohra等[7]研究了一类具有无穷时滞的分数阶微分方程, 并利用公理化定义的相空间的方法得到了初始值为0时解的存在性; 在此基础上, Dong[8]通过引入加权无穷时滞分数阶微分方程的概念, 研究了初始值非0时解的存在性以及对初始数据的连续依赖性; Chen等[9]通过利用一个分数阶积分的比较性质以及相关不动点定理, 研究了一类具有无穷时滞的非线性分数阶微分方程解的存在性和Hyers-Ulam稳定性．稳定性分析是微分方程的一个重要方面, 目前Hyers-Ulam稳定性理论因其在数值模拟、物理学、生物学等领域不易找到精确解问题中的重要意义而被广泛研究[10-11]．受上述文献启发, 本文拟研究一类具有无穷时滞的变系数线性分数阶微分方程, 通过一些假设条件并利用Banach压缩映射定理和Leray-Schauder不动点定理, 探讨该类微分方程解的存在性和唯一性, 再通过一类Gronwall不等式, 分析在无穷时滞条件下该类分数阶微分方程的Hyers-Ulam稳定性．

1 预备知识

本文研究如下具有无穷时滞的变系数线性分数阶微分方程:

(1)

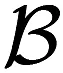
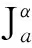
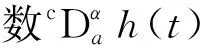
其中m∈N+且α∈(m-1,m]．

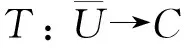
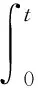
2 解的存在性

引理5分数阶微分方程(1)的解y的形式为

为了证明下面的定理, 给出以下几个假设条件:

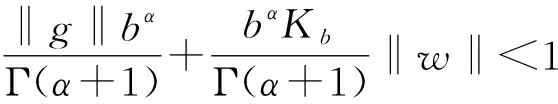
证明 由上述分析可知, 如果y是问题(1)的解, 当且仅当y满足

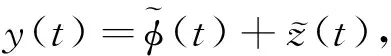
定义集合E={z∈C((0,b],R)}, 则E是闭且完备的．定义算子P:E→E为

(2)

则由Leray-Schauder不动点定理, 通过以下4步可证明算子P是连续的且是一致连续的．

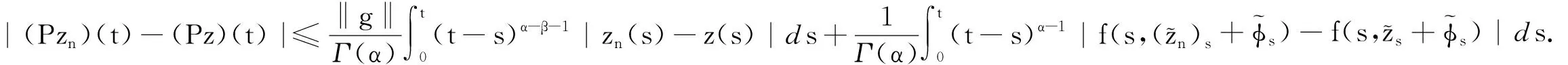
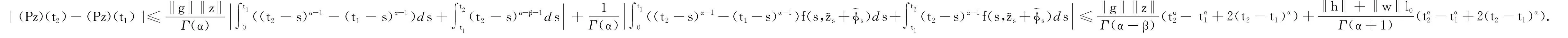
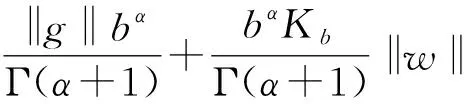
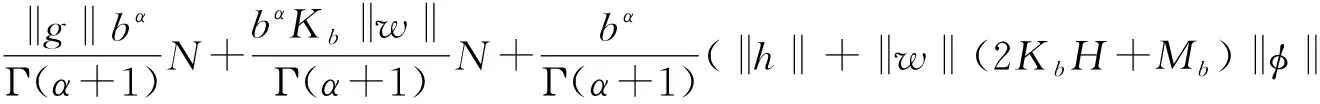
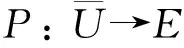
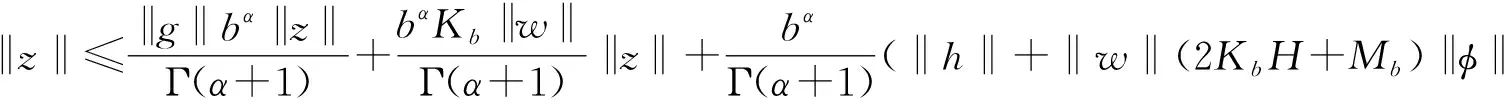
注因为在无穷维空间中, 连续函数在有界闭区间上不一定是一致连续的, 故须给出假设条件(H1)来保证函数一致连续性．

定理2若条件(H1)和(H3)成立, 且对任意的t∈I, 不等式

成立, 则问题(1)在(-∞,b]上至少有一个解．

证明 算子P由式(2)定义, 则该定理可通过如下4个步骤来证明．

i)P是连续的．与定理1的证明相似, 由勒贝格控制收敛定理及条件(H3)易验证算子P是连续的．

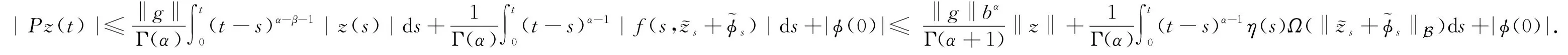
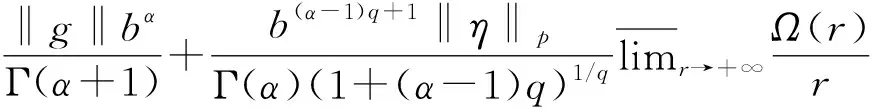
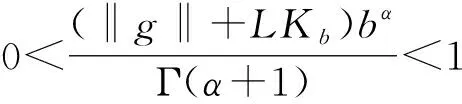
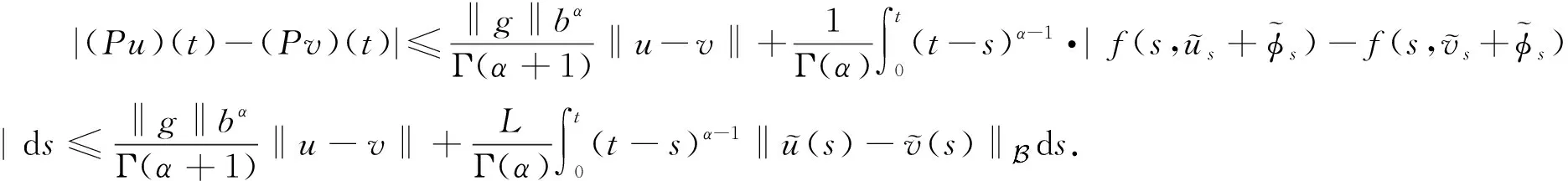
3 Hyers-Ulam稳定性分析

定义4若存在一个常数p>0, 使得对于任意的ε>0, 对所有满足不等式

的解u(t)都存在问题(1)的一个解v(t), 使得|u(t)-v(t)|≤pε成立, 则问题(1)是Hyers-Ulam稳定的．

定理4如果定理3中的条件全都成立, 则问题(1)是Hyers-Ulam稳定的．