基于宽深学习的P2P借款人违约风险预测
张桃宁 梁雪春
(南京工业大学电气工程与控制科学学院 江苏 南京 211816)
0 引 言
P2P借贷市场是基于互联网的交易平台。相较于传统金融交易平台,其交易成本更低、贷款更便利[1-2]。随着我国对P2P的监管力度不断加深,P2P产业告别了野蛮式发展,平台逐渐朝着健康发展的道路转型[3]。然而,平台与投资者之间仍然存在信息不对称的问题,投资者易投资遭受损失,平台也会因过多的不良贷款而逐渐失去投资人的信任[4]。从长远来看,提高不良贷款的识别率、降低投资风险,对平台方和投资者来说都非常必要。
章雷等[5]认为增大数据量可以减轻信息不对称所带来的影响,更大的数据量能更好地评估借款人资质。不平衡数据少数类存在分类精度较低的问题,增大数据量可以避免因欠采样而导致模型过拟合[6]。通过获取大量的借款人信息数据,挖掘借款人信息与贷款违约的关联性可以使投资者制定更加合理的投资策略,降低投资风险。在国内P2P风险预测研究中,谭中明等[7]使用人人贷数据,采集了约900个样本,12个特征。张卫国等[8]也采用人人贷数据,共采集了1 500个样本,有17个特征。谢雪梅等[9]从人人贷和拍拍贷上选取了共约65 000个样本进行预测。可以看到,由于国内大多数平台不会公布其历史借款人信息,研究者收集到的数据集的数据量较少,且格式不统一,不利于模型的比较分析。本文选用目前全球最大的P2P平台Lending Club官方公开的借款人信息数据集,具有时间跨度大、数据量大和数据特征丰富的优势,也是近年来在P2P借贷违约预测和风险评估领域内研究者们较为青睐的数据集,具有一定的基准性[10-12]。
国内外学者对借款人违约风险预测模型进行了许多研究,Teply等[13]基于Lending Club数据集,对比了10种主流分类算法的性能,其中逻辑回归、神经网络和线性判别分析在分类任务中性能较好。Wang等[14]对P2P网贷数据进行了特征的相关分析,研究表明,在特征数量(158个)较大的情况下,逻辑回归分类准确率最高。吴艇帆[15]对逻辑回归分类器进行了改进,使用基于L1正则化的逻辑回归模型进行P2P借款人风险测度,提升了预测的准确性。Guo[16]使用BP神经网络作为贷款的风险评估算法,通过比较后得出,基于BP神经网络的算法优于传统的Logistic回归算法。上述研究表明,逻辑回归和神经网络在借款人违约预测的应用中都能取得较好的结果。谷歌公司Cheng等[17]提出了应用于推荐系统的宽深度学习模型,该模型结合了宽模型(即逻辑回归模型)记忆性强和深模型泛化能力强的优点。本文采用宽深度学习模型对P2P借款人违约概率进行预测,但由于推荐系统数据集与借款人信用数据集有明显区别,借款人信用数据集的类别型特征维数较低且原始模型没有加入数值型特征。因此需要改善模型嵌入层的输入并加入数值型特征。最后在数据量大、特征数多的真实借款人信息数据集上验证该模型的预测性能。
1 模型介绍
1.1 宽模型
宽模型部分选用的是广义线性模型,即大规模分类问题中常见的逻辑回归模型[14]。宽模型能够更好地捕捉特征之间的相关信息,具有良好的记忆性。设模型的输出为y,y是一个0到1之间的概率值,表示借款人的违约概率,y越接近1表示违约概率越大。计算借款人违约概率的公式为:
y=σ(z)
(1)
(2)
式中:zwide表示宽模型的输出;σ(·)为Sigmoid函数;借款人违约风险预测问题是一个二分类问题,标签为1的样本为违约样本,标签为0的样本为非违约样本,故采用二分类任务中常用的Sigmoid函数将模型的输出转换为0到1之间的概率值,最后将违约概率大于0.5的样本预测为违约样本。宽模型预测的借款人违约概率为y=σ(zwide),zwide计算方法如下:
(3)
式中:x=[x1,x2,…,xn]为特征向量;wwide=[w1,w2,…,wn]为模型权重;bwide为偏置。
组合特征不仅能获取类别型特征之间的交互信息,而且能用线性模型学习非线性信息,提高模型的泛化性。宽模型的输入除了原始类别型特征之外还需增加组合特征。对于借款人数据集,特征向量x包括数值型特征和类别型特征,即x=[xnum,xcat]。为丰富宽度模型的输入,可以利用类别型特征xcat构造组合特征φ(xcat),组合特征定义如下:
(4)
式中:xcat表示所有原始的类别型特征,xi为单个类别型特征,xi∈xcat;d是组合特征的个数;cki是一个布尔型的变量,cki=1表示第i个原始特征xi参与了第k个组合特征φk的特征交叉。如特征“性别”={男,女}与特征“职业”={老师,学生}可以交叉组合成“新特征”={(男,老师),(女,老师),(男,学生),(女,学生)}。加入组合特征φ(xcat)后,式(2)改写为:
(5)
式中:φ(xcat)=[φ1(xcat),φ2(xcat),…,φd(xcat)]为新增的d个组合特征。宽模型的结构如图1所示。
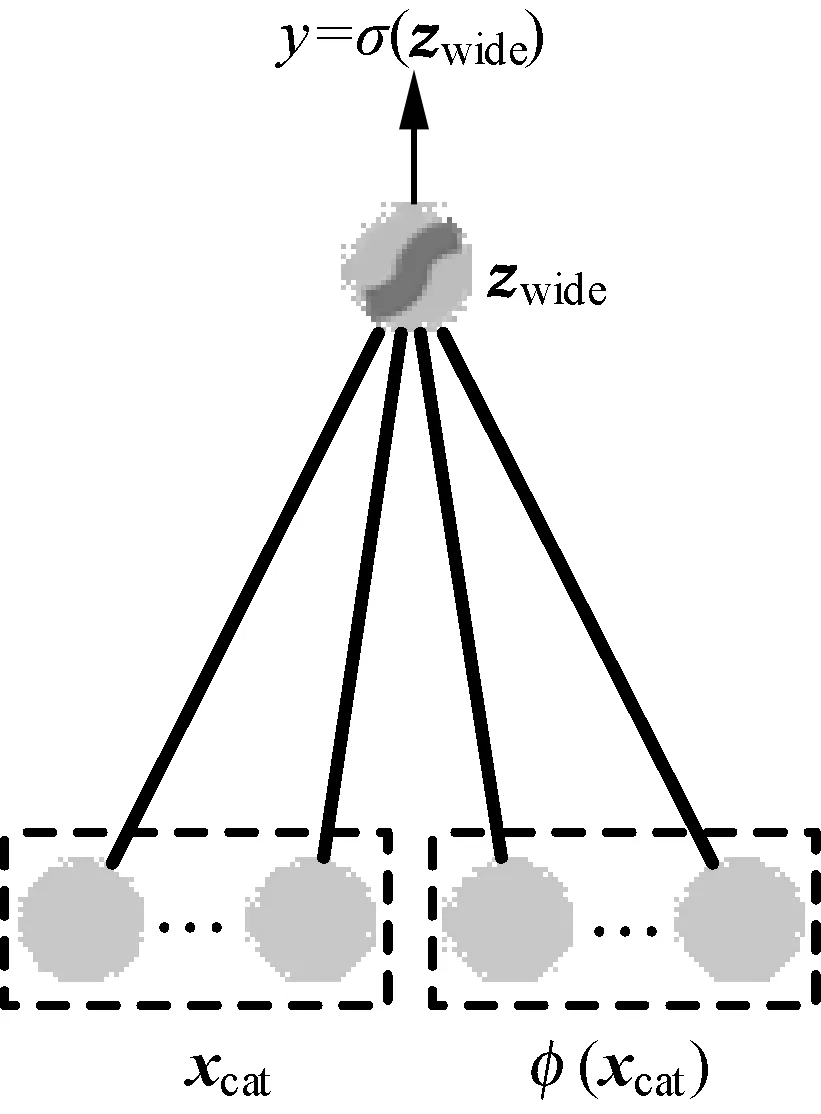
图1 宽模型结构
1.2 深模型
深模型部分是前馈神经网络[16]。深模型的输入包括数值型特征xnum、类别型特征xcat与组合特征φ(xcat)。其中,对于原始类别型特征和组合特征这类稀疏特征,需要将其映射为稠密实值向量。用embed(x,k)表示将类别型特征x映射为k维的嵌入向量,则深模型的嵌入向量为:
xemb=[embed(xcat,k1),embed(φ(xcat),k2)]
(6)
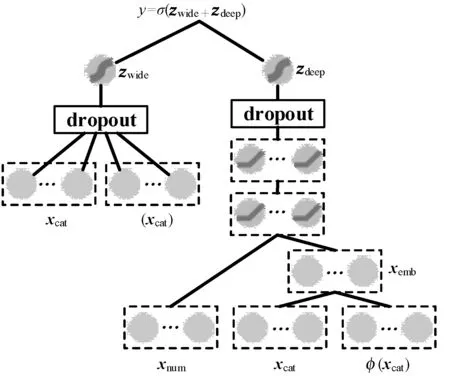
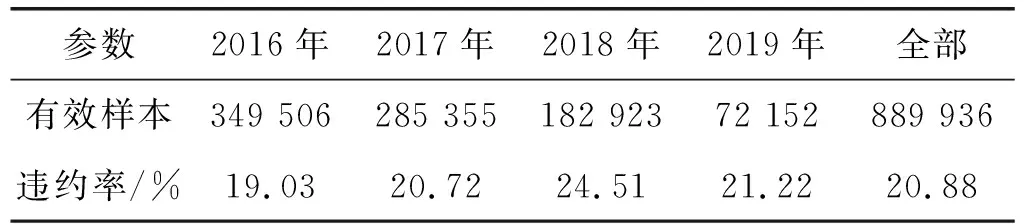
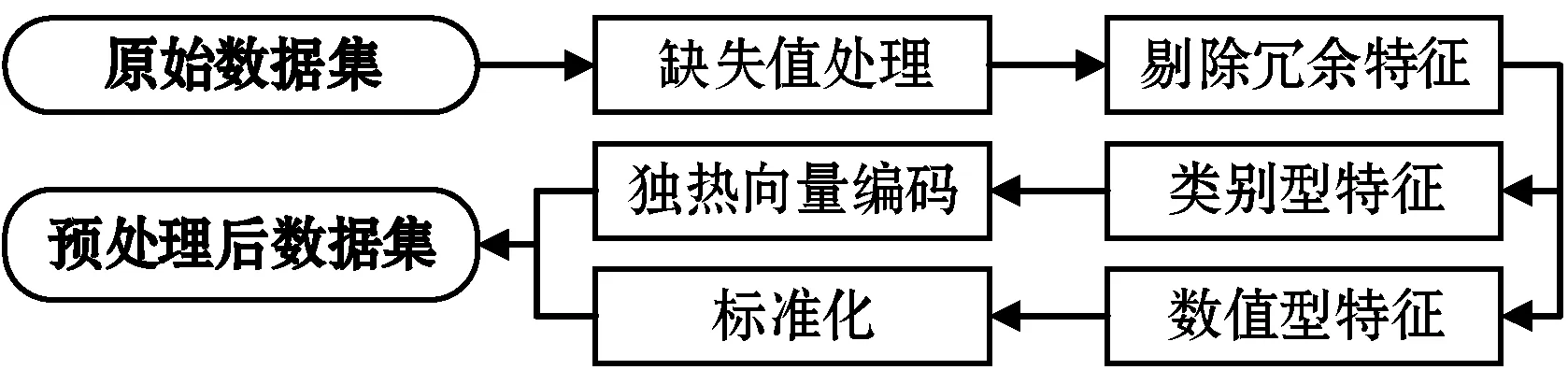
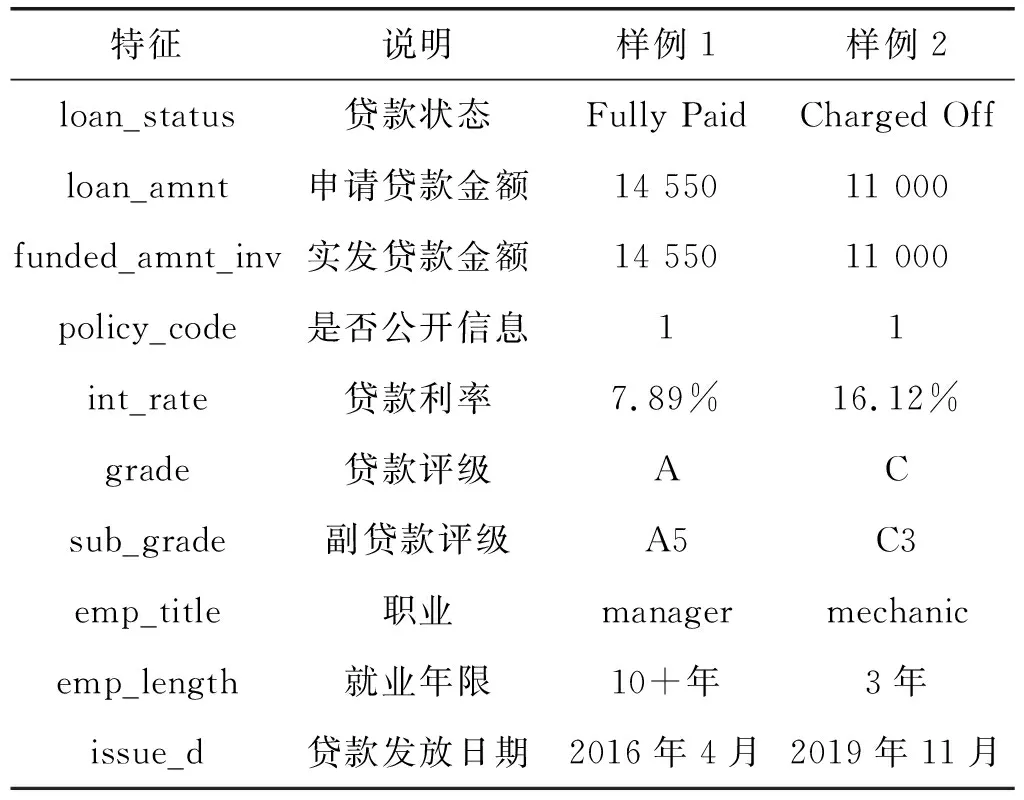
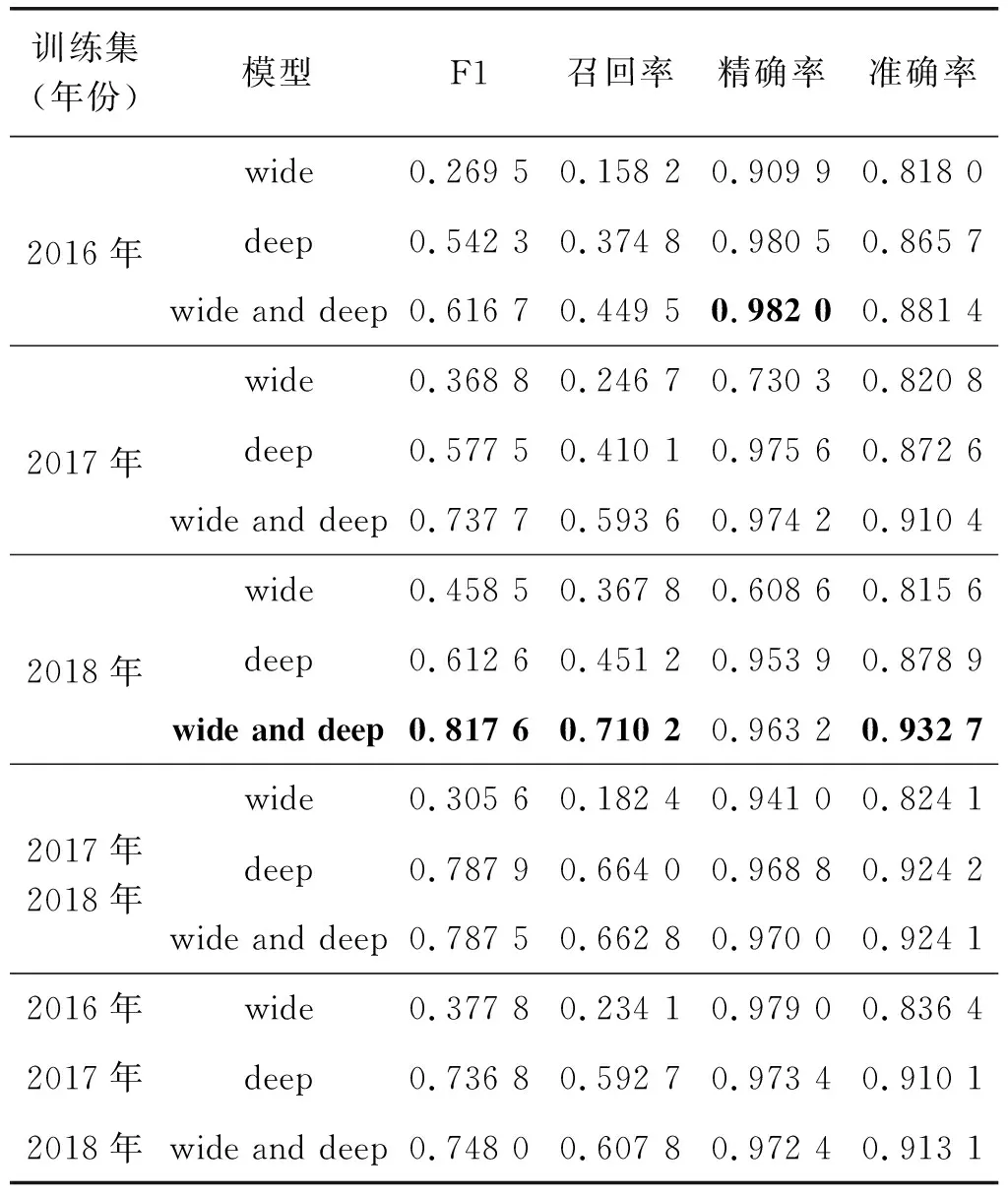
式中:k1、k2表示映射后的维度。原始类别型特征因其本身的维度较低,映射后的嵌入向量要比组合特征的嵌入向量维数更低,即k1 数值型特征xnum与映射后的嵌入向量xemb拼接后作为神经网络的输入接入第一层隐藏层,则第一层隐藏层的输出z(1)为: z(1)=f(W(1)[xnum,xemb]+b(1)) (7) 其余各层隐藏层的输出如下: z(l+1)=f(W(l)z(l)+b(l)) (8) 式中:l为当前隐藏层层数;z(l)、b(l)与W(l)是第l层的输出、偏置及权重;f为激活函数,此处为线性整流函数(Rectified Linear Units, ReLU)。ReLU激活函数公式如下: f(x)=max(0,x) (9) 设深模型共有L层隐藏层,则最后一层隐藏层的输出为z(L),利用式(1)计算违约概率。对于深模型,式(1)中的z=zdeep。 (10) 式中:wwide与bwide为深模型输出层的权重和偏置。深模型结构如图2所示。 图2 深模型结构 宽深模型由宽模型和深模型共同组成[17],采用逻辑回归损失函数来进行联合训练。此处宽度部分和深度部分的模型是联合训练,而非组合模型训练。组合模型在训练过程中,两模型独立训练,分别优化其参数,损失函数也独立。而在联合训练中,宽深度部分共享一个损失函数,在训练过程中同时优化两模型的参数。对于预测借款人违约概率的二分类问题,将宽模型和深模型的输出之和输入至式(1)计算得到违约概率: y=σ(zwide+zdeep) (11) 式中:zwide和zdeep分别由式(5)和式(10)给出;σ(·)为Sigmoid函数,由式(2)给出。 为了避免过拟合,增强模型的鲁棒性,本文在宽模型和深模型的输出层加入dropout随机失活层[18],设定一个概率p,对输出层的每个输出都以概率p来判定是否保留该输出,将式(5)改进为: (12) 式中:⊙表示两向量对应元素相乘;r=[r1,r2,…,rn],n的大小与[x,φ(xcat)]的维度一致;ri∈{0,1}通过以概率为p的伯努利分布随机生成。 同理,将式(10)改进为: (13) 同时,为了提高精度并加快训练速度,避免模型过于关注取值较大的特征,在特征输入隐藏层之前需要对数值型特征进行标准化,本文采用Z-Score标准化,标准化公式如下: (14) 式中:μ和σ为数值型特征的均值和标准差。 本文提出的宽深模型针对借款人数据的特点加入了数值型特征,更充分地利用嵌入层对数据进行压缩和降维,丰富了模型的输入的同时,扩展了模型的适用性。宽深模型结构如图3所示。 图3 宽深模型结构 实验选用目前全球最大的P2P平台LendingClub的借款人信息数据集。选用的数据时间范围跨度从2016年至2019年,共约190万个样本。原始借款人数据集共有144个特征,其中以“loan-status”(贷款状态)项作为判断借款人是否违约的目标标签,由于还款时限和贷款策略的不同,存在贷款状态未完结的样本,需要剔除掉这部分无效样本。可以看到,年份越近,有效样本数越少,剔除掉无效样本后,剩下约90万条有效样本,违约率表示违约样本数占有效样本数的比例,数据集相关信息如表1所示。 表1 Lending Club数据集信息 由于原始数据集的缺失值较多,且存在部分取值为字符串型的类别型特征,无法直接应用到模型训练中。因此需要对数据集进行基本的数据预处理工作。 首先删除缺失值占比超过15%的特征,由于缺失值数目过多,这些特征对模型训练帮助有限。其次对于缺失值占比小于5%的特征,删除掉有缺失值的样本。剩下缺失值占比为5%~15%的特征中,对于特征取值分布符合正态分布的数值型特征用均值填补缺失值,其余特征用0值填充。对于类别型特征,缺失值用出现频率最高的特征值填充。 删除相关度高的特征,如“funded_amnt” (申请贷款金额)和“funded_amnt_inv” (实发贷款金额)特征。该数据集中借款人的贷款申请都得到了通过,因此这两项特征的取值高度一致。 删除特征取值频率高于98%的特征,例如对于“policy_code”(是否公开信息)特征,取值为“1”的样本占比高达99%。 数据预处理完成后,将特征分为类别型特征和数值型特征分别进行简单的特征工程。对于类别型特征,对其进行独热向量编码,将一维类别型变量映射成多维的取值为0或1的特征。对于数值型特征,对其进行标准化。 最后将预处理完毕后的特征汇总成新的数据集。数据预处理部分的流程如图4所示。 图4 数据预处理流程 实验环境为Chromium OS 9.0, Intel(R) Xeon(R) CPU @ 2.30 GHz, 8 GB内存, Tesla K80 12 GB GPU显存, Python3.7, TensorFlow 2.2.0。在完成数据预处理后搭建训练模型。实验使用TensorFlow深度学习框架搭建模型。深度部分由两层隐藏层组成,结点数分别为64和32。使用Adam优化器优化交叉熵损失函数,学习率为10-4,迭代轮次为10,每批数据有2 048个样本。 本文采用召回率、精确率和准确率等指标衡量模型性能。正例表示违约样本,负例表示非违约样本。TP表示实际是正例,预测为正例的样本数;FP表示实际为负例,预测为正例的样本数;TN表示实际为负例,预测为负例的样本数;FN表示实际为正例,预测为负例的样本数。 召回率为模型找到的违约样本数与实际违约样本数的比例,其定义如下: (15) 精确率为模型找到的违约样本数与预测违约样本数的比例,其定义如下: (16) 准确率的定义如下: (17) F1-score的定义如下: (18) 由于数据集特征数量较大,表2仅给出前文提到的和少数新增的包含部分特征的样本样例表。 表2 包含部分特征的样本样例表 表3 不同训练集下3个模型的性能对比 为了验证数据集大小及时间对模型性能的影响,本文采用按年份对数据集进行的划分方式对模型性能进行验证。实验使用2016年至2018年的样本作为训练集,2019年的数据作为测试集,模拟投资者根据过去的信息对未来进行决策的过程。将预处理完毕后的训练集数据以一年为单位,对数据集进行组合划分,然后分别对宽模型、深模型、宽深模型进行训练。 可以看出,以2018年作为训练集得到的模型性能最佳,模型的召回率、准确率、F1-score分别为71.02%、93.27%、81.76%。此外可以看出,以2016年、2017年,2018年的样本作为训练集时,年份越接近2019年,模型的F1-Score、召回率、准确率越高,精确率有小幅下降。这说明由于经济时空背景的差异,年份越久远的样本对预测违约概率的贡献程度越低,使得模型在利用过去的样本进行训练时,得到的模型较为保守,找出违约借款人样本的能力较差,虽然精确率较高,但投资者更为重视的召回率偏低。 同时可以看出,以2018年、2017年至2018年、2016年至2018年的样本作为训练集时,随着数据集样本数的增加,模型的F1-Score、召回率、准确率也在下降。说明盲目增加数据量并不一定能提升模型性能,反而可能会因降低了样本质量而导致模型性能下降。 图5展示了以2018年作为训练集训练得到的三个模型在训练过程中性能指标的迭代曲线,可以看出,宽深模型在准确率和F1-score指标上的性能均优于单一的宽模型或深模型。其中,宽模型的性能最差且上升慢,需要更多的训练迭代轮次来提升宽模型的性能,而宽深模型各项指标随迭代次数的上升明显快于深模型和宽模型。宽深模型准确率和F1-score分别比深模型高5.38百分点和20.5百分点,该实验结果表明了宽深模型应用于借款人违约预测的可行性与优越性。 为提高不良贷款的识别率、降低投资风险。本文针对大数据时代下的借款人信息数据集数据量大和特征丰富的特点,提出一种基于宽深学习的借款人违约风险预测模型。该模型结合了宽模型的记忆性和深模型泛化性,并采用引入随机失活层对其进行优化。在进行数据预处理后,将数据集以年份为单位划分并训练模型。实验结果表明,选用最新的数据进行投资决策分析和模型训练对投资者而言十分重要;宽深模型具有更强的识别违约样本的能力和更好的预测性能。本文仅采用了单平台的借款人信息数据集,后续研究可以结合多家平台的借款人信息数据集训练模型,提高模型的泛化能力并进一步拓展宽深模型的应用范围。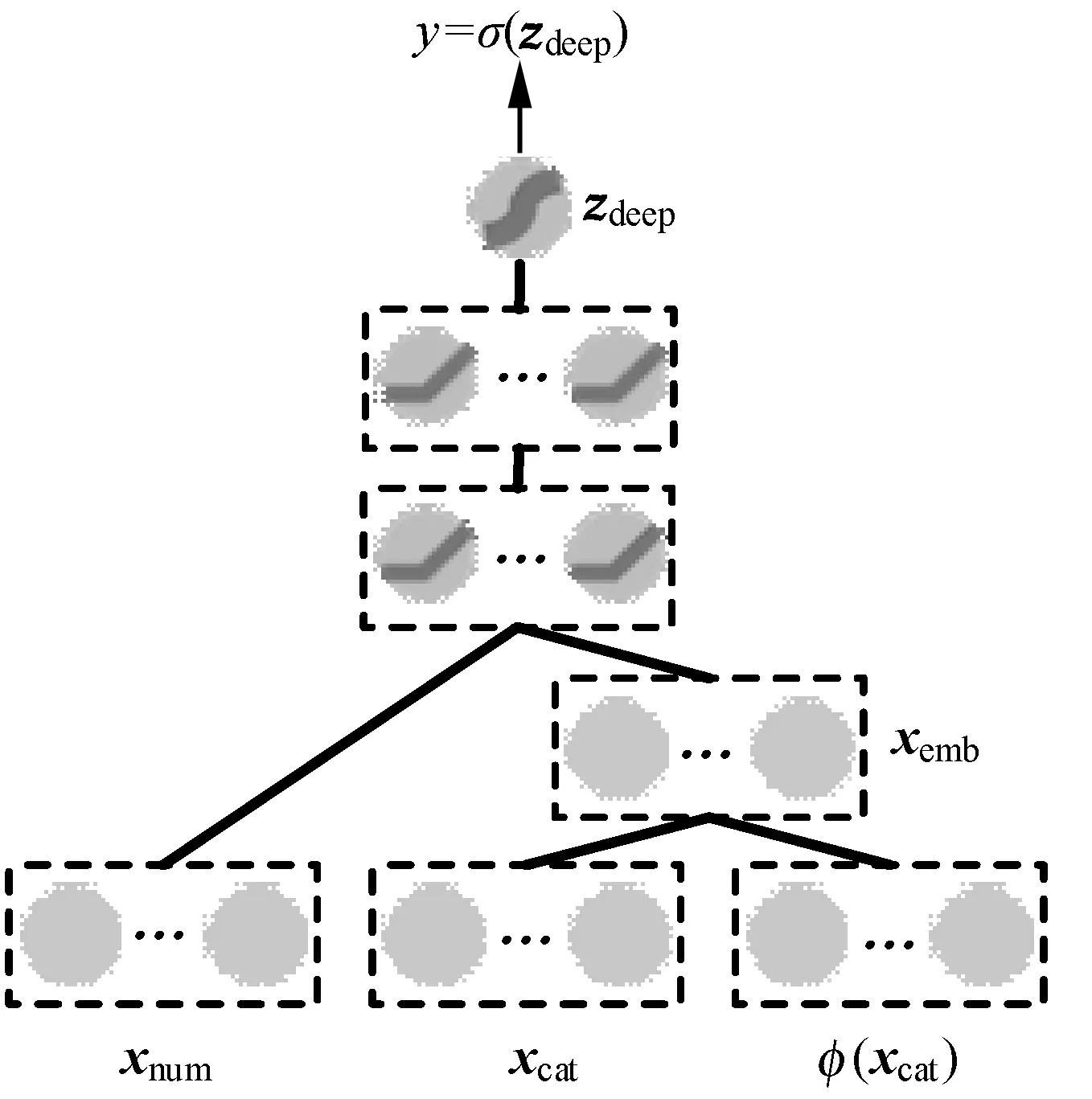
1.3 宽深模型
2 数据预处理
2.1 数据集
2.2 缺失值处理
2.3 剔除冗余特征
2.4 特征工程
3 实验与结果分析
3.1 实验环境和模型参数
3.2 评价指标
3.3 结果分析
4 结 语

