基于边界变化的索结构自振频率测试机理

申成庆，胡迎新，黄方林，李显方，周德，雒明波，周天睿

(1. 中南大学 土木工程学院，湖南 长沙，410075；2. 湖南中大设计院有限公司，湖南 长沙，410018；3. 中铁第四勘察设计院集团有限公司，湖北 武汉，430063)

索力调整是悬索桥、斜拉桥和拱桥等含索结构施工过程中的关键工序，对桥梁线形和最终成桥状态具有重要影响。合理的索力调整离不开精准的索力测量，工程中常用测量方法有2种。第一种为直接测量法，如压力表法、磁通量法和压力传感器法[1]等，这些方法通过仪器直接读出索力，数据可靠但布设繁琐且造价高昂，多用于特大桥在运营期的健康监测。第二种为间接测量法，即通过测试结构频率、挠度、线形等参数，经理论换算得到索力，所得索力与理论计算方法密切相关，常用计算方法有静力法和动力法2 种。其中，静力法常见有“三点弯曲法”，即通过测量桥梁整体或局部线形，建立索力与线形之间的函数关系，进而求得索力，这种方法在实际操作时，常受限于现场索结构具体形式而影响适用性[2-3]。动力法主要有频率法、地脉动法[4]和模态识别法[5]等，即通过测量桥梁动力特性，根据索力与动力特性间函数关系求得索力。其中，频率法以操作简单、快捷且经济实用等特点而成为现场索力测试最常用的方法，而地脉动法和模态识别法由于使用条件相对苛刻，在实际测量中运用不多。

频率法是一种通过测试索结构自振频率来确定索力的方法。这种方法由张紧弦理论发展而来，前提是需精准采集索结构自振频率。但对于索结构来说，其自振频率受诸多因素如环境温度[6-8]、索结构抗弯刚度[9]、边界条件与额外支撑条件[10-11]、阻尼器设置[12]和索结构损伤情况[13-14]等因素影响，其中，索结构抗弯刚度和边界条件的影响最直接，且两者取值难以确定。在实际工程中，索结构的边界条件常常介于固结与铰接之间[15]，且与具体施工阶段密切相关，边界条件存在不确定性。目前对索结构边界条件的研究多通过拟合公式再结合实际情况进行解释说明[16]，需对“长索结构”与“短索结构”进行分类讨论。分析“短索结构”时，为使拟合值更准确，需考虑更多因素[17]。尽管如此，采用拟合公式的方法在实际测量中的效果仍然较差。

在实际运营中，“短索结构”比“长索结构”更易发生如断丝和锈蚀等破损现象[18]。对“短索结构”自振频率的精准测量是目前工程中亟待解决的问题。然而，如何在索结构中区分“短索结构”目前还尚无定论。有学者直接按索结构长度来判断[19]，也有学者提出采用Irvin 参数和抗弯刚度影响系数等[20]对“短索结构”进行判定，其不足之处是难以应用于实际测量，且无法解释在测量“短索结构”自振频率时无法得到稳定值的现象。为此，本文在考虑索结构抗弯刚度前提下，对索结构在转动约束和平动约束这2种边界条件下自振频率的变化进行理论分析。引入参数长细比，推导索结构在不同边界条件下自振频率与长细比之间的函数关系，并提出一种通过长细比判断“短索结构”的方法，对“短索结构”实测频率不稳定的原因进行分析。同时，通过有限元仿真分析对本文提出的计算理论进行验证，以浙江舟山新城大桥为例，验证长细比判定方法在工程中的可行性与适用性。

1 不同边界条件下频率法适应性理论分析

索结构两端边界条件的理想情况为一端固结而另一端铰接，在实际工程中，索结构的边界条件都只是接近理想情况。已有研究表明，在复杂边界条件下，索力与自振频率之间的关系符合超越方程，分析索结构的边界参数变化对自振频率的影响十分困难。为此，考虑索结构两端受转动约束和平动约束2种边界条件，对索结构的自振频率与长细比、抗弯刚度和边界条件等参数的关系进行理论分析。

1.1 索结构两端受转动约束

在对动力特性进行分析时，考虑抗弯刚度的索结构可等效为两端受拉的梁，如图1所示。假定索结构采用匀质材料，索结构两端边界处平动刚度无穷大，则索结构的平衡微分方程可表示为

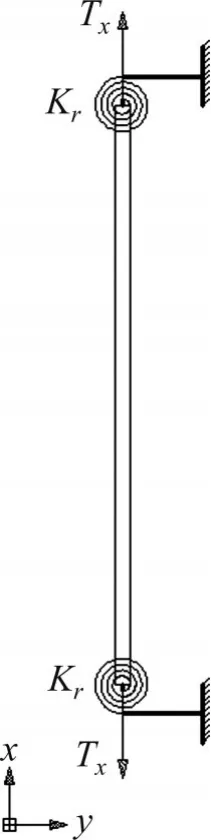
图1 两端转动约束时索结构的计算模型Fig. 1 Calculation model for cable structures under rotational constraint at both ends

式中：E为弹性模量；I为截面惯性矩；w(x，t)为y方向位移；Tx为索力；m为单位长度质量。边界条件为

式中：Kr为转动刚度；L为计算长度。

式(1)中索力通常可表示为

当索结构不考虑自身抗弯刚度时，索力Tx可表示为

式中：a和b为边界转动刚度系数，参考文献[20]，a的取值范围为[3.5, 4.0]，b的取值范围为[1.0,3.0]；n为自振频率阶次；fsn为索结构考虑抗弯刚度的第n阶自振频率；fn为不考虑抗弯刚度的第n阶自振频率。由式(4)和式(5)可得

式中：η为频率比，反映由刚度变化引起的频率变化程度。为更好地考察边界条件影响，引入索结构长细比λ：

式中：A为面积。由式(6)和式(7)可得

当a=4，n=1 时，由式(8)可得：。

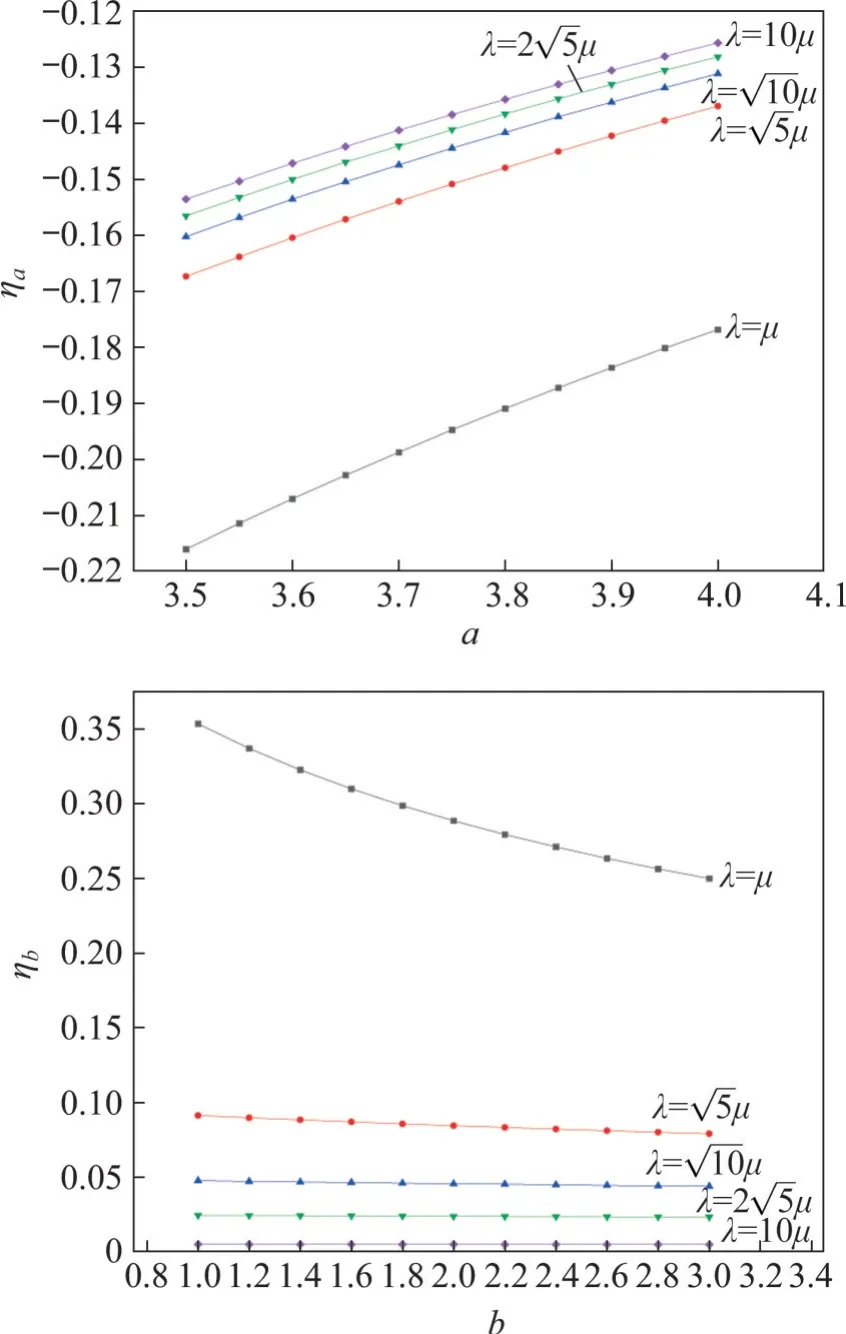
图2 转动约束下ηa和ηb随长细比λ的变化曲线Fig.2 Variation curve of ηa and ηb with aspect ratio λ under rotational constraint

上述分析表明：随着长细比λ增大，灵敏度系数ηa和ηb均下降；当λ足够大时(λ大于)，灵敏度系数ηb趋于0。在工程实际中，长索结构的长细比较大，因此，采用频率法可测得其稳定的自振频率。当长细比λ较小时(如λ＜μ)，灵敏度系数ηa和ηb随系数a和b的变化均较大。在工程实际中，短索结构的长细比λ较小，采用测量锤敲击“短索结构”时，会造成短索结构的边界条件发生随机变化，这正是无法获得“短索结构”稳定自振频率的原因。

1.2 索结构两端受平动约束

考虑图3所示索结构，令索结构上、下两端的平动约束刚度分别为K1和K2，平衡微分方程同样可由式(1)表示。

图3 两端平动约束时索结构的计算模型Fig.3 Calculation model for cable structures under translational constraint at both ends

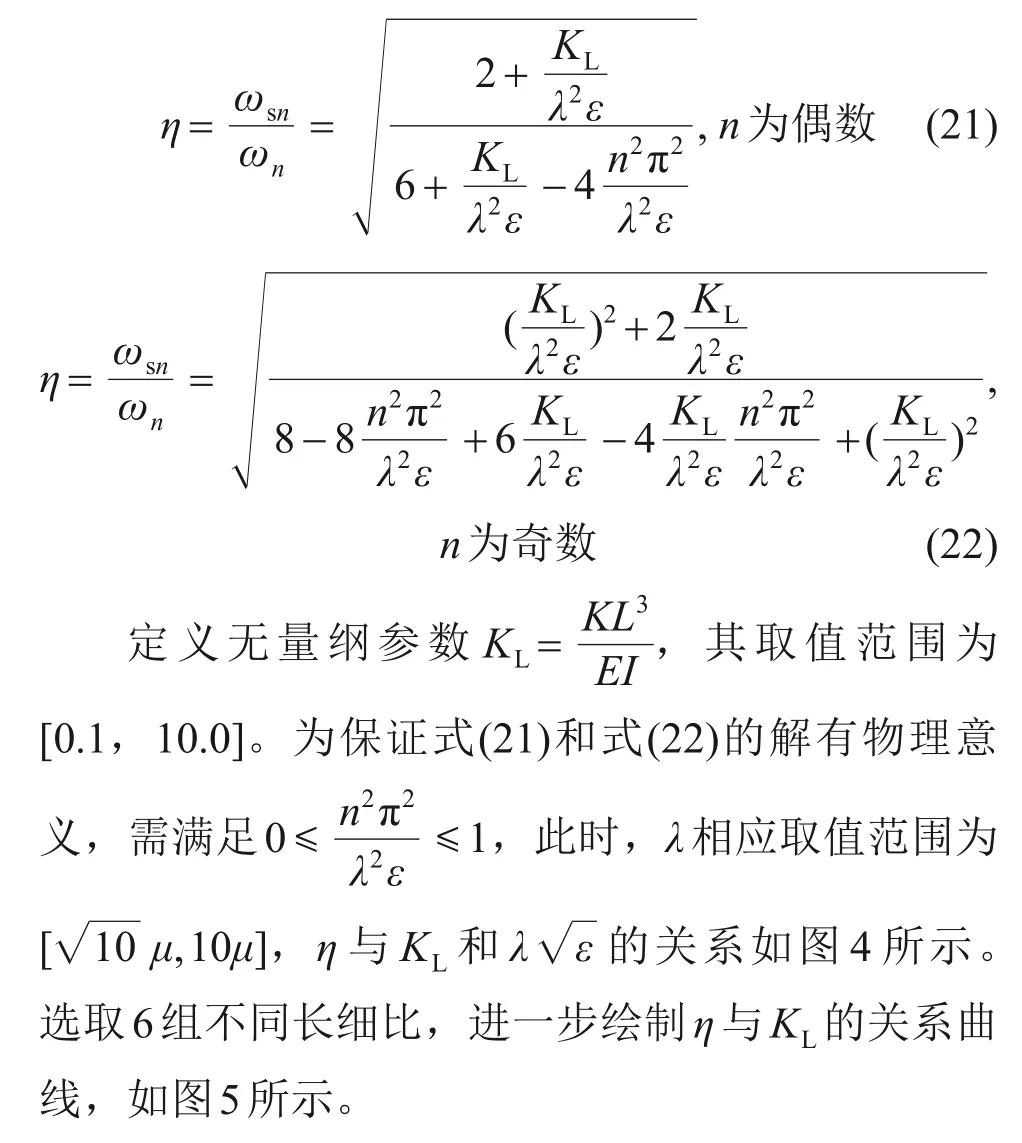
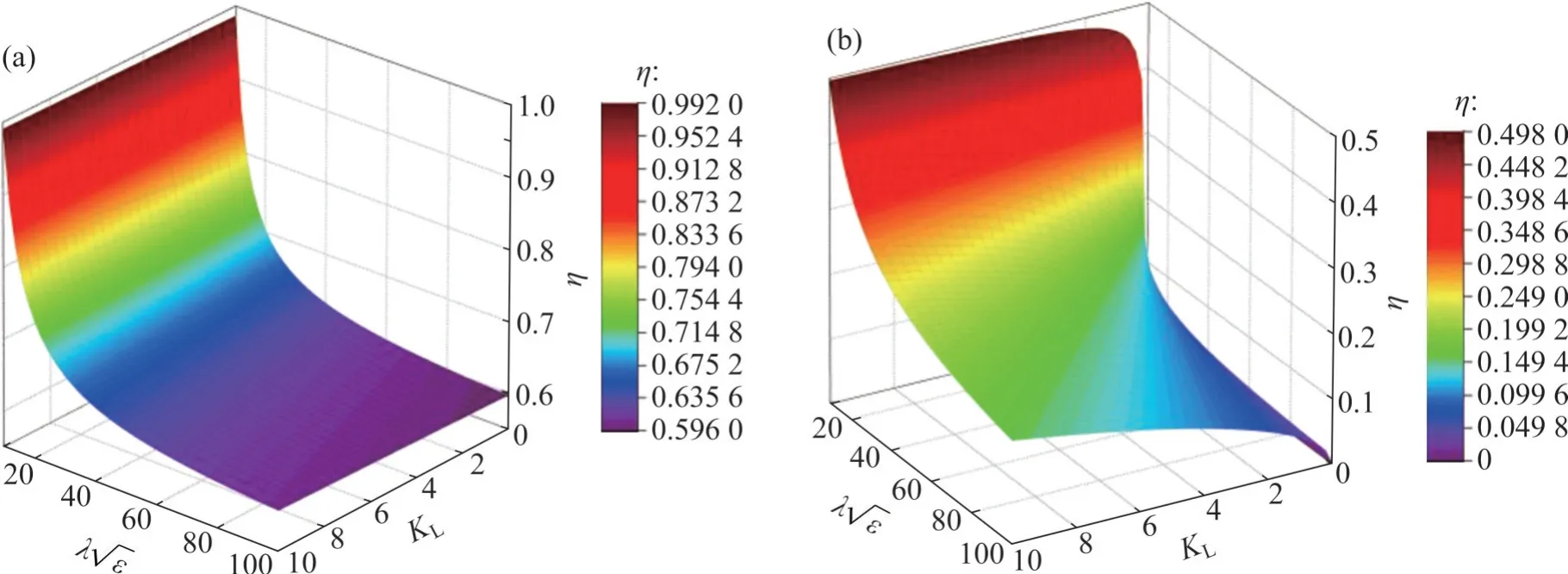
图4 频率比η随KL和λ的变化(n=1)Fig.4 Variations of frequency ratio η with both KL and λ(n=1)

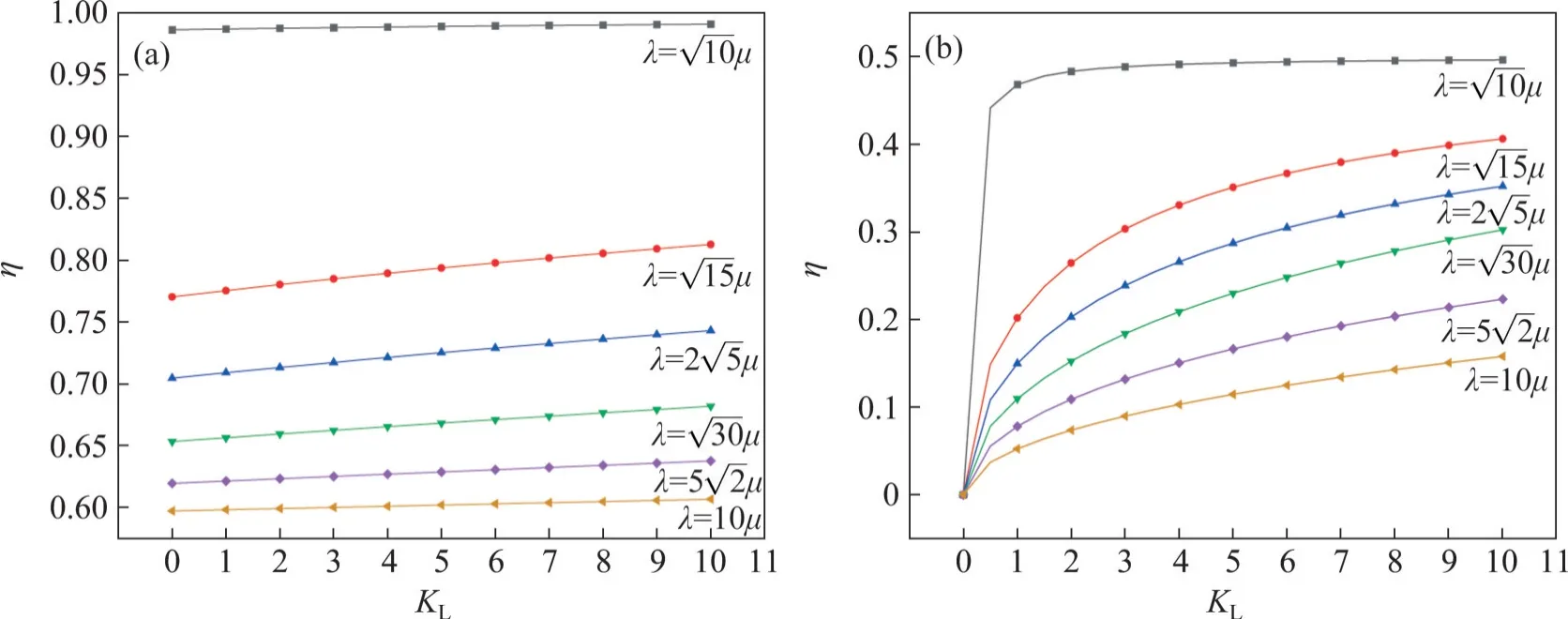
图5 频率比η随KL的变化Fig.5 Variation of frequency ratio η with KL

图4(b)与图5(b)表明：当自振频率阶次为奇数时，频率比η在KL小于1时变化较大；随着长细比λ增大，η变化趋于平缓。

在实际工程中，索结构KL一般都大于1。当KL为[1，10]时，频率比η对KL并不敏感。可见，平动约束不是“短索结构”自振频率测不准的主因。

综合平动约束与转动约束的分析结果可知：当索结构长细比λ小于、采用频率法测试索结构自振频率时，不能忽略边界条件尤其是边界转动刚度变化带来的影响，因此，可将长细比λ作为“短索结构”的一种判据。

2 有限元模拟验证

采用通用有限元软件ABAQUS进行仿真分析。根据前述分析可知，索结构两端边界的转动刚度变化是其自振频率测不准的主因，因此，在模拟边界条件时，只考虑改变边界的转动刚度，忽略其平动刚度。

图6所示为有限元模型示意图，材料属性见表1。考虑5 种不同直径(分别为10、20、30、40 和50 mm，为方便起见，相应索结构名称分别记为S10、S20、S30、S40和S50)的索结构，索结构两端的边界条件通过空间梁单元模拟。

图6 有限元模型示意图Fig.6 Schematic diagram of finite element model

表1 材料属性Table 1 Material properties

进行有限元分析时，通过控制索结构的单元数量确保计算的收敛性，收敛性验证计算结果见表2。从表2 可见：随着单元数量增加，第1 阶自振频率计算结果趋于稳定；当单元数量大于100个时，计算结果收敛性较好，模型满足分析要求。

表2 不同单元数量下模型第1阶自振频率收敛性验证计算结果Table 2 The first natural frequency of the model with different number of elements

式中：Dc为直径判据，直径大于Dc的索结构为“短索结构”。

将表1 中材料属性数据代入式(23)可得Dc=29.5 mm，即直径大于29.5 mm 的索可认定为“短索结构”。

在实际工程中，索结构的边界条件通常难以确定，本文采用2 种方式来处理。第一种是以S20和S50为分析对象，边界处转动刚度取索结构抗弯刚度0.1倍到10倍。第二种是以所有索结构为分析对象，边界处转动刚度取S50抗弯刚度的0.1 倍到10倍。

第一种方式的计算结果见图7(a)和7(b)。从图7(a)和7(b)可见：对于“长索结构”S20与“短索结构”S50，当边界处转动刚度从索结构抗弯刚度0.1倍增加到1 倍时，2 种索的第1 阶自振频率均有较大幅度增加(S20和S50的第1 阶自振频率分别增加11.59 Hz和49.19 Hz)；当边界处转动刚度从索结构抗弯刚度的1倍增加到10倍时，第1阶自振频率增幅变小(S20和S50第1 阶自振频率分别增加9.23 Hz和15.43 Hz)。

第二种方式的计算结果见图7(c)。从图7(c)可见：对于“长索结构”S10和S20，频率比η变化极小，增幅均不超过0.01，说明“长索结构”的自振频率对边界处转动刚度的变化不敏感；S30的频率比η增幅约0.05；“短索结构”S40和S50的频率比η变化较大，增幅分别为0.15和0.30，说明“短索结构”的自振频率对边界处转动刚度的改变较敏感。

在上述2种方式下，不同直径索结构自振频率和频率比计算结果验证了本文“短索结构”判定依据的可行性和有效性。

3 工程实例验证

舟山新城大桥改扩建工程主桥采用(36+148+36) m飞燕式钢箱系杆提篮拱结构形式，主桥全长220 m。主跨拱肋矢高37 m，矢跨比为1/4，全桥设13 对吊索，吊索沿顺桥向垂直布置，标准间距为8 m，吊索编号见图8，吊索型号除HL1 为镀锌钢丝拉索PES(C)7-91 外(其中，PES 指镀锌钢丝吊索，C指黑色内层、彩色外层的双层结构，7-91指吊索含7 股钢丝束，每股钢丝束中包含91 根细钢丝线，其余依此类推)，其余吊索均采用镀锌钢丝拉索PES(C)7-73。本文对吊索(HL1 至HL7)进行现场实测和分析。

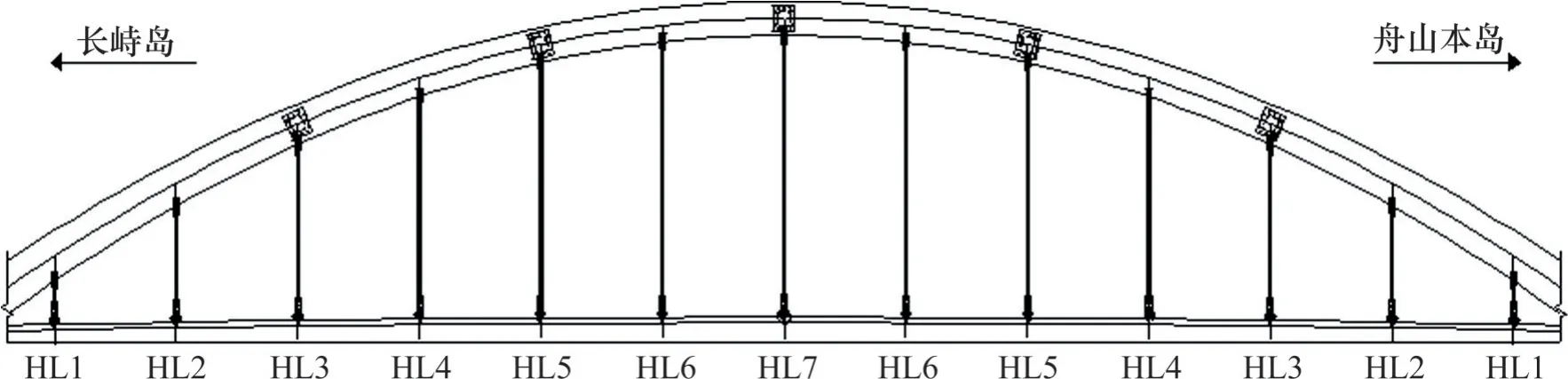
图8 新城大桥吊索编号Fig. 8 Xincheng Bridge cable identification number

采用基于频率法的索力检测仪对吊索自振频率进行测试，结果见表3。在测试过程中，吊索HL1 与吊索HL2 无法通过索力检测仪采集到稳定的自振频率，2组吊索的索力通过千斤顶张拉反算得到。

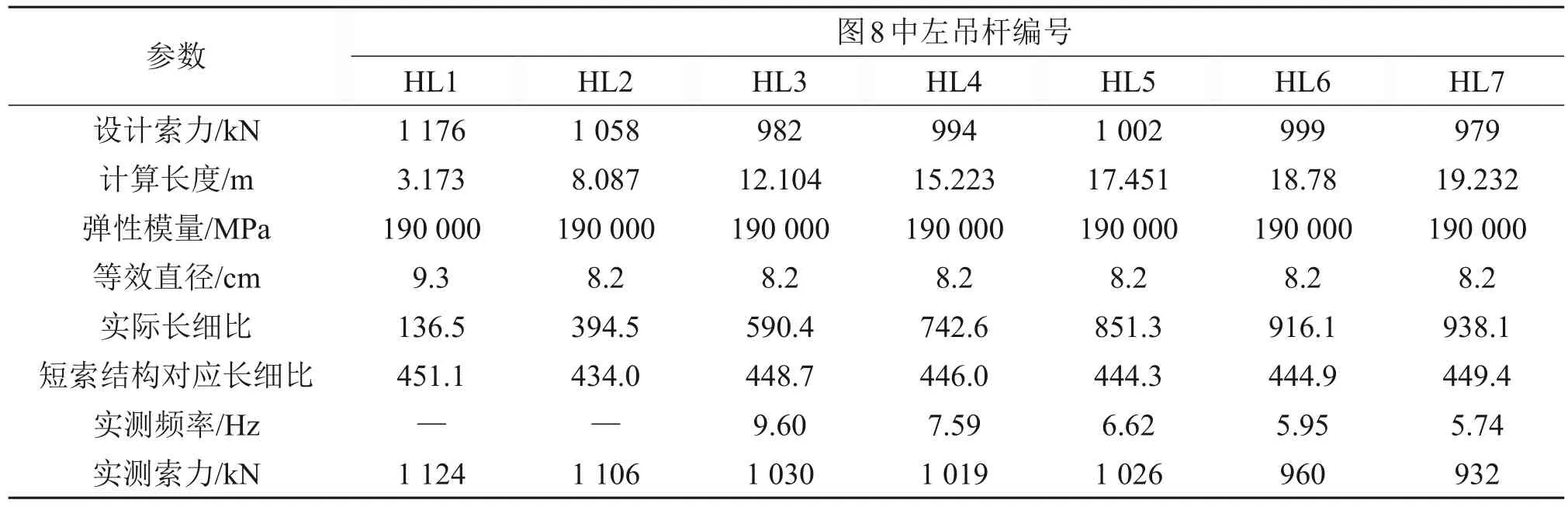
表3 新城大桥吊索实测频率Table 3 Measured frequency of the suspension cable of Xincheng Bridge

根据本文提出的“短索结构”判据，吊索HL1 和HL2 均为“短索结构”，理论上，这2 组吊索无法获得稳定的自振频率。这与表3所示结果一致，从而验证了长细比判据的工程适用性。

4 结论

1) 引入长细比作为“短索结构”的判据，操作性强，并具备通用性。

2) “短索结构”的边界条件(尤其是转动刚度)受扰动影响发生随机变化，这是频率法无法测得稳定自振频率的主要原因。

3) 本文提出了“短索结构”自振频率测试机理，从理论上验证了“短索结构”无法获得稳定自振频率，且理论结果与仿真结果和现场实测结果均较吻合，验证了长细比判据的工程适用性。