面向大型工业仓库的多AGV综合优化调度方法
胡恩泽,贺建军,申帅,吴仁超
(中南大学 自动化学院,湖南 长沙,410083)
随着仓储物流技术的发展,许多大型工业仓库采用大规模的自动引导车(AGV)编队来实现物料自动运输,其每天需要处理几千起搬运任务,如何优化调度使AGV 更高效地执行任务成为当前提升物流效率和降低仓储成本的关键问题。AGV 调度最重要的目标是最小化任务完成时间,其受到多项决策的影响[1]:
1) 任务定序分配。决定分配给每个AGV 的任务及执行这些任务的顺序。
2) 路径规划。为AGV 执行被分配的任务时选择最优路径,通常最优路径为耗时最少或距离最短的路径。
3) 冲突管理。解决各AGV 之间可能发生的碰撞冲突。
以上3个问题是相互依存的[2],确定AGV的任务分配是计算路径规划的先决条件,在选择AGV的执行路径后才能判断碰撞冲突是否会发生[3]。大多数研究针对调度优化的3 个问题提出了求解的方法[4-5]:
首先,在不考虑碰撞冲突的情况下单独求解任务定序分配问题,得到最优方案[6];
然后,为该方案选择最优的执行路径;
最后,考虑冲突管理问题,在发生冲突时建立“交通规则”等策略,指导AGV 停车等待或绕行来避免碰撞[7]。
然而,AGV 按照最优的任务定序分配方案生成的最佳路径去执行任务时,很可能存在大量的碰撞冲突情况[8],频繁等待或绕行会降低AGV 整体系统运行效率[9]。这些研究忽略了AGV 避免冲突的规避操作,导致存在计算之外的“延迟时间”[10],无法实现系统整体的最优调度。综上分析,调度中的3个问题是内在关联的,任务定序分配结果会对路径规划中碰撞冲突情况造成直接影响[11]。因此,在AGV 优化调度问题中,任务定序分配、路径规划和碰撞冲突问题需要经一体化综合处理,进而得到系统整体的最优调度方案[12]。
针对AGV 综合调度问题,MAZA 等[13]提出了预先规划算法和实时路由算法,在路径规划过程中生成无冲突路径。LIAN等[14]提出一种基于交通控制方法的综合调度方法,实现了基于时间窗的调度和冲突管理。然而,这些方法不能有效提高AGV 整体系统效率。SINGH 等[15]研究了电量约束下的异构AGV 综合求解任务分配和路径规划问题,并提出了一种自适应大邻域搜索算法。然而,该方法没有考虑AGV 之间的碰撞冲突。此外,一些基于精确算法的综合调度优化方法[16-17]被用于一体化求解任务定序分配和无冲突路径问题,但任务定序分配结果对路径规划中造成的碰撞冲突情况无法确定,这些方法对每一种情况进行分析时,需要消耗不合理的计算时间,无法应用于大型工业仓库实例。
针对以上问题,本文提出一种综合优化调度方法,体现在:
1) 建立一个混合整数线性规划模型来描述异构多AGV 的综合调度问题,采用栅格法构建仓库地图,定义任务执行过程,提出路径专家库的概念,即所有候选路径的集合。针对现实工业仓库对于AGV在速度与物料搬运能力的异构性和AGV需要在适当时间充电等问题,制定相应的约束条件。
2) 提出一种基于分层规划的综合优化调度方法,将综合调度问题分解为聚合的上层任务定序分配问题和下层路径规划问题,在不考虑冲突的情况下生成上层问题的精英解集合,依次对集合中每个解在下层进行基于路径专家库的路径规划计算,记录碰撞冲突结果并生成禁忌列表,将禁忌列表作为碰撞冲突的约束条件融入上层问题寻优过程,最后通过迭代搜索得到满足整体性能最优的调度方案。
3) 提出一种混合离散状态转移算法(HDSTA),设计一种精英种群生成方法,引入路径选择程序和禁忌列表,提升算法搜索过程的多样性能力与强化搜索能力。同时,为了在任务定序分配结果中合适的位置插入充电请求,提出2种插入算子。
1 调度模型



2 基于分层规划的综合调度方法
本文提出一种基于分层规划的综合优化调度方法,将调度问题分解为聚合的上层主问题和下层子问题。上层问题决定AGV 任务定序分配决策,下层子问题计算执行任务的最优路径,同时,在2层问题的计算过程中考虑碰撞冲突问题。综合优化调度方法首先在不考虑冲突的情况下生成上层问题的精英解集合;然后,依次对集合中的每个精英解在下层进行基于路径专家库的路径规划计算,计算碰撞冲突并生成禁忌列表;最后,将禁忌列表作为碰撞冲突的约束条件融入上层问题的寻优过程中,通过迭代搜索得到满足整体性能最优的调度方案。
AGV可以通过硬件和“交通规则”避免碰撞,因此,无冲突路径不是强制性的,但规避冲突造成的延迟时间(避免碰撞的等待或绕道时间)需要被量化,同时,在上层问题和下层问题求解过程中减少碰撞冲突,目标是最小化AGV 运输时间,即最小化所有AGV执行任务时间和延迟时间(避免碰撞的等待或绕道时间)的总和。此外,为了避免死锁,不允许2 辆以上AGV 在同一位置发生冲突,存在这种情况的调度方案在计算过程中会被定义为不可行解。综合优化调度方法执行步骤如下。
步骤1:在上层主问题中去除碰撞约束条件,定义AGV 每个任务的运输时间为从起始节点到交付节点的最短时间,计算任务定序分配最优解,并将最优解和计算过程中其他精英解放入1个集合φi中。φi中的每个解用pn表示,其中,pn在集合φi中按照目标函数值升序排列。
步骤2:在下层问题中,对于φi中每一个解pn进行冲突约束下的路径规划,同时生成一个带有记忆的碰撞冲突约束列表,称为禁忌列表。若路径规划可以找到无冲突路径,则调度优化结束;否则,将碰撞冲突结果记录到禁忌列表中。在每一个pn计算碰撞冲突过程中,将具有最小目标函数值的解记为暂定最优解pt,其碰撞冲突造成的延迟时间用td表示。
步骤3:定义最大允许延迟时间为ε,若步骤2中推导的td小于ε,则调度优化完成。
步骤4:重新求解上层主问题,在这过程中从φi中去除被记录在禁忌列表中的解。若k次迭代后目标函数值没有降低,则调度优化结束。否则,更新精英集合φi并跳转到步骤2。
本文提出一种引入路径搜索和禁忌列表的混合状态转移算法(HDSTA)对任务定序分配、路径规划和碰撞冲突问题进行一体化求解,算法流程如图1所示。首先,在考虑当前禁忌列表下,针对任务定序分配问题求解出候选精英解并添加到精英解集中,再依次对新生成的精英解执行基于路径专家库的路径规划计算。然后,通过碰撞检测程序确定冲突延迟时间并获得最终的任务完成时间。最后,更新禁忌列表,并将其作为冲突判断指导求解下一代候选精英解。
混合离散状态转移算法流程如图1 所示,其中,Xbest代表当前最优解,fbest表示历史最优解,SE为种群数量,n,ma,mb和mc为0到1之间的小数。HDSTA 的伪代码见算法1。算法开始于由不考虑冲突的DSTA(I)算法生成上层初始精英解集Q0,对于其中每一个解pn,通过路径选择程序(SP)生成下层路径解p,计算运输时间T、延迟时间tp和冲突次数,并生成禁忌列表Tlist。HDSTA设计了3个终止条件:
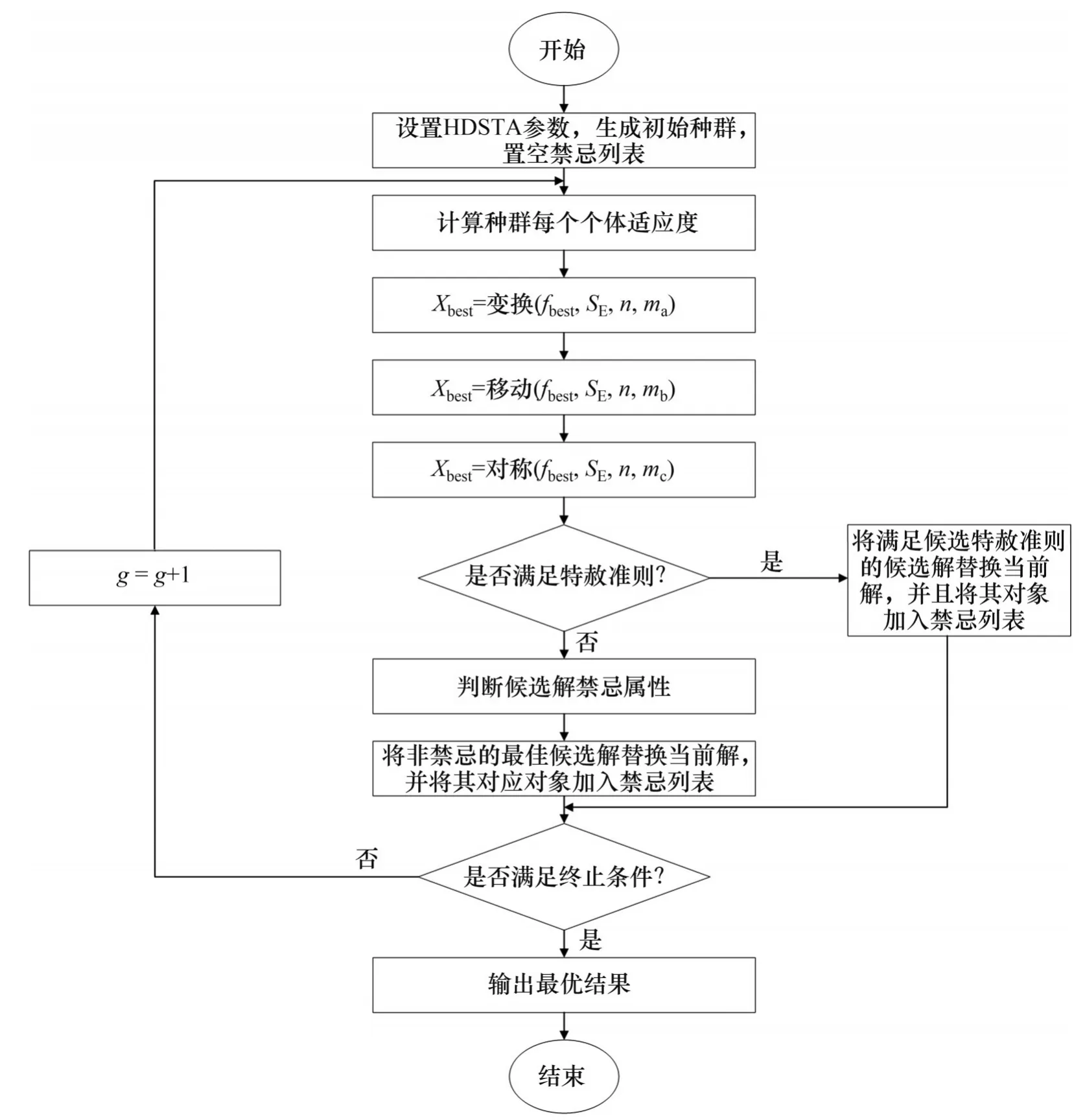
图1 混合离散状态转移算法流程Fig. 1 Flow chart of hybrid discrete state transition algorithm
1) 精英解集中存在1个解,在路径规划中可以生成无冲突路径,算法结束,输出最优解;
2) 精英解集在路径规划中的最优解,其延迟时间tbest小于目标值ε,算法结束,输出最优解;
3) 迭代l次后目标函数值没有减少,算法结束,输出当前最优解。精英解集通过融合禁忌列表约束的DSTA(II)迭代过程进行更新,直到其中一个终止条件被满足,生成包含定序分配解D和执行路径解Pbest的综合调度解S。
2.1 生成精英解集
在搬运任务序列中插入定位充电请求对AGV调度问题至关重要。当AGV 当前电量无法完成所有被分配的任务时,必须在中途充电,此时,需要在搬运任务序列中合理的位置插入充电请求,并规定AGV 在距离先前服务任务位置最近的充电站进行充电[18]。针对AGV 可能需要多次充电问题,定义AGV 完成所有搬运任务需要的充电次数为Nk,设计临界插入算子和非临界插入算子。当决定了1 个搬运任务定序分配解时,对Nk>1 的AGV 用临界插入算子插入充电请求,对Nk=1 的AGV用非临界插入算子插入充电请求。

算法1:HDSTA伪代码输入:AGVK,任务T,路径专家库Ns输出:S 1:用DSTA(I)算法生成初始精英解集Q0 2:while (y1=1 or y2=1 or y3=1)3:for每一精英解pn ∈Q0 4:[p,T,tD,SD]←SP(pn)5:if tp=0 then 6:D ←pn;Pbest ←p;Tbest ←T;y1 ←1 7:break for;8:end if 9:if tp <tbest then 10:tbest ←tp;Pbest ←p;Tlist ←[pn,Sp];Tbest ←T 11:end if 12:end for 13:if tbest <ε then 14:y2 ←1 15:end if 16:if y1=0 or y2=0 then 17:采用DSTA(II)算法更新精英解集Q0 18:更新计数器l 19:if l >5 20:y3 ←1 21:end if 22:end if 23:end while 24:S ←(D,Pbest)
临界插入算子(CI):按顺序确定AGV 电量低于临界阈值bl的任务位置,并在该任务前插入充电请求。
非临界插入算子(NCI):按顺序确定AGV电量低于临界阈值bl的任务位置。在该任务前找到离充电站最近且不会增加充电次数的位置,将充电请求插入该最佳位置,使AGV提前充电。
DSTA采用群体中的最优解在邻域内迭代搜索直到找到全局最优解。为了保证任务定序分配结果对路径规划过程具有多样选择性,需要生成包含多个精英解的集合。在DSTA迭代过程中,下一代种群的生成只与上一代的最优解相关,用于生成种群的3 种特殊状态变换算子见文献[19]。每一代种群中的解具有高度相似性,其包含的解不满足精英性和多样性要求,因此,不能作为精英解集。针对上述问题提出一种精英解集Q0生成方法。初始化解集Q0并定义集合中解的数量上限为m,按照目标函数值升序存放。在迭代过程中,将每一代搜索的所有精英解与Q0中存放的解进行比较,若存在更优的解则进行替换,从而保证精英解集Q0包含搜索过程中所有精英个体。引入插入算子的精英解集生成方法见算法2,其中,Se为种群数量,Sbest为种群中最优解,Q0为精英解集,Ci与Ni分别为临界插入算子和非临界插入算子。
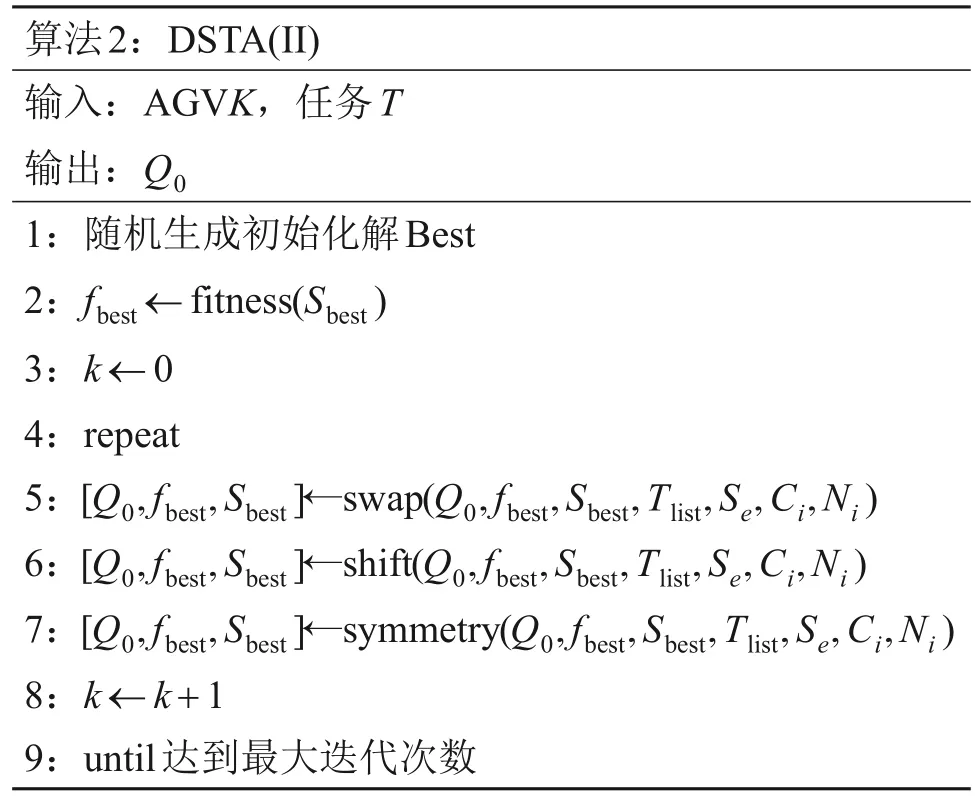
算法2:DSTA(II)输入:AGVK,任务T输出:Q0 1:随机生成初始化解Best 2:fbest ←fitness(Sbest)3:k ←0 4:repeat 5:[Q0,fbest,Sbest]←swap(Q0,fbest,Sbest,Tlist,Se,Ci,Ni)6:[Q0,fbest,Sbest]←shift(Q0,fbest,Sbest,Tlist,Se,Ci,Ni)7:[Q0,fbest,Sbest]←symmetry(Q0,fbest,Sbest,Tlist,Se,Ci,Ni)8:k ←k+1 9:until达到最大迭代次数
2.2 路径选择
基于路径专家数据库的AGV 路径选择程序SP,其伪代码见算法3。路径选择过程根据当前任务定序分配方案,从路径专家数据库中找到冲突最少的执行路径Pbest,计算延迟时间tp并记录冲突信息生成禁忌列表Tlist。为了求解路径规划方案P,定义dk为AGVk被分配的所有搬运任务,其执行路径由rk表示。每个任务搬运任务tn∈dk由1 个取货请求和1 个送货请求组成,代表执行任务tn的路径,其中,分别表示取货路径和送货路径。此外,当任务为充电请求时,则只有1 条路径。在路径专家库中,从站点i到站点j的路线rij中第n条路径用p(i,j,n)∈Ns表示。
在选择程序中,冲突检测程序(Con)是一个基于三维时空模型的冲突检测程序[20],它能计算冲突路径位置Sp与延时时间ti。当路径之间存在冲突时,替换程序(Replace)在路径专家数据库中用其他平行路径替换当前路径,替代方式是从路径候选解集中自上而下搜索,直到为每个AGV 从路径库中找到延迟时间最少的路径。在找到无冲突执行路径后停止搜索,否则,替换程序将搜索路径专家库中冲突路线的替换路径,选择延迟时间最小的路径集合记为当前最优路径解Pbest。

算法3:路径选择程序输入:任务定序分配方案Pn,路径专家库Ns输出:Pbest,tp,Tlist 1:TC←0 2:for 每一个dk ∈pn 3:for 每一个tn ∈dk 4:rnu←P(ot u,1);rnu'←P(otd,1)5:rn(1:)←rnu;rn(1:)←rnu′;rk(n)←rn 6:end for 7:P(k)←rk 8:end for 9:[ti,Sp]←Con(P)10:if ti≠ 0 11:for 每一个Sp 12:repeat 13:P′ ← Replace(SP,P)14:t′i ← Con(P')15:if t′i <ti 16:Sp′←Sp ti ←t′i P ←P′17:end if 18:until 路径库中所有的路径都被查询19:end for 20:tp ←ti 21:else 22:tp ←ti;Pbest ←P 23:end if 24:if tp满足被禁忌列表记录的条件25:Tlist ←[pn,Sp]26:end if
禁忌列表在HDSTA 中的作用是从搜索空间移除曾经访问的解,从而进行更广泛探索。在路径选择中,禁忌列表记录并更新存在冲突较多的任务定序分配精英解。HDSTA 在迭代过程中更新精英解集时受到禁忌列表约束,并删除被记录的解,从而防止循环回到之前搜索过的解决方案。禁忌列表能存储解的数量上限为h,当新的解延迟时间更大时,禁忌列表才会更新。需要强调的是,本文考虑的冲突问题具有时序性,优先被执行的任务不受靠后被执行任务的影响,禁忌列表中记录的信息对于任务分配结果的约束可以被扩展,如当AGV1被分配执行任务(2-1-3-5)且AGV2被分配行任务(8-7-6-4)时,若记录AGV1在执行任务1 会与执行任务7 的AGV2发生冲突,则冲突信息可以被扩展为AGV1(2-1-X-X)与AGV2(8-7-X-X),其中,X表示任意一个任务。
3 工业仓库实例验证
3.1 工业仓库案例
湖南长沙的某科技公司是本项研究的合作单位和实验应用场所,某仓库的布局如图2所示,包括40个预分拣站和9个充电站。采用1个包含背负式AGV和托盘式AGV的异构车队集群,2种AGV的速度分别为0.8 m/s 和1.0 m/s。根据从业者反馈,在1 个时间段内,等待分配的平均任务数约为50个,繁忙期,等待分配的任务超过80个。

图2 仓储布局Fig. 2 Warehouse layout
3.1.1 参数设定
在实验案例中对参数进行设定,首先确定种群数量、精英解集中解的数量和禁忌列表长度的上限分别为S e=20,m=30,h=120。然后,确定算法的终止条件参数,允许的最大延迟时间ε=85 s,HDSTA 迭代计数值为5 次,DSTA 最大迭代计数值为50次。路径专家库Ns在离线阶段被提前预设,每一条站点之间的路线都包含10 条以上优秀的候选路径。
3.1.2 案例分析
基于实际仓库案例的背景,通过处理不同规模的问题验证方法的有效性。在实验中,待调度的AGV数量分别6、9和15辆,案例中待分配的任务数分别为20、30、40、50、60、70 和80 个,每一个案例随机生成5 组任务,并运行10 次,共运行50 次程序,取平均值作为结果。当前工业仓库中先进AGV 系统普遍采用依次优化的调度方法,其中LIAN 等[14]提出的方法最具有代表性,因此,在现实仓库案例分析中选择该方法进行对比验证。在案例分析中,综合优化调度方法和依次优化调度方法的任务完成时间和延迟时间的对比结果如图3至图5所示。
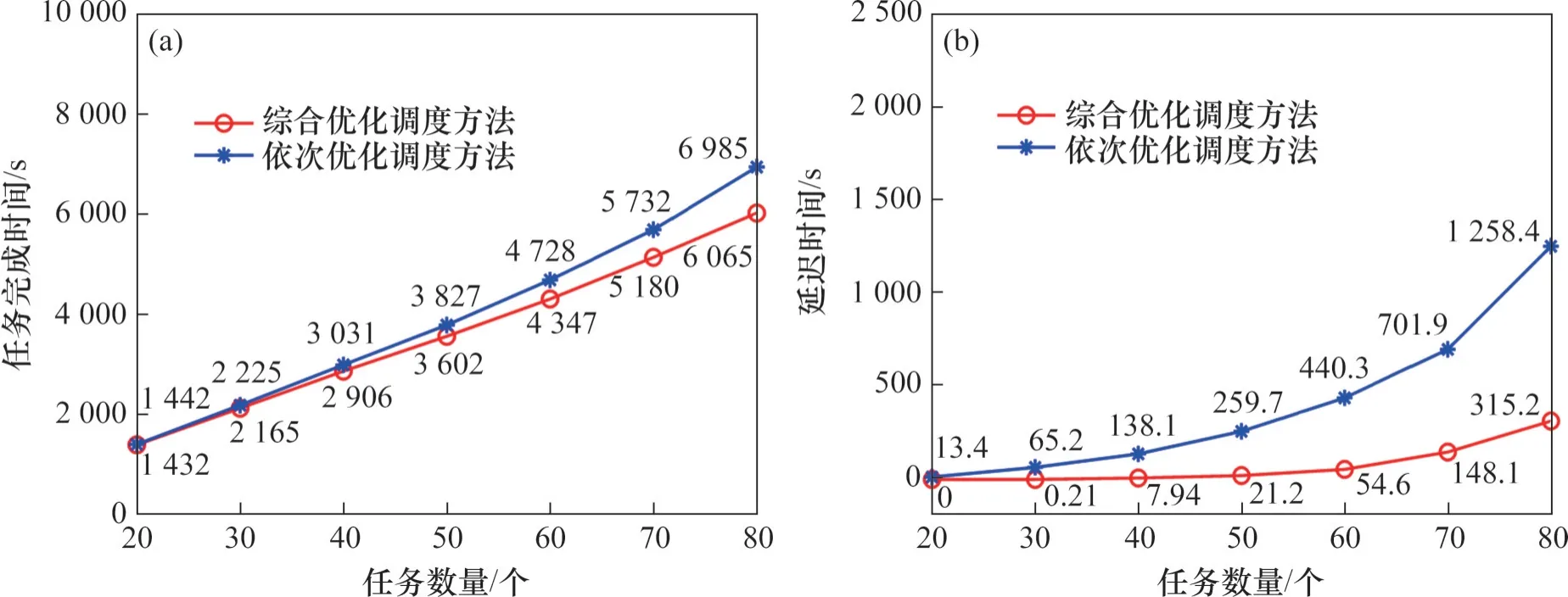
图3 使用6辆AGV的任务完成时间和延迟时间对比分析Fig. 3 Comparative analysis of task completion time and delay time with 6 AGVs
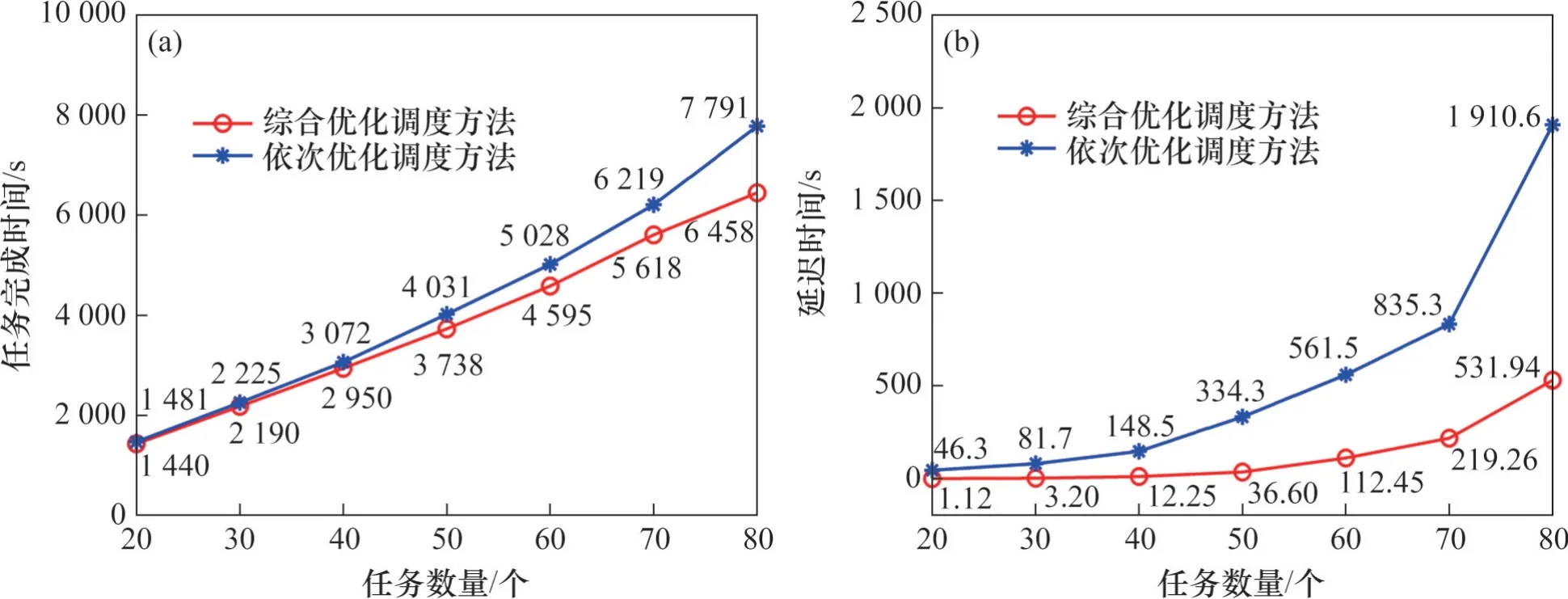
图4 使用9辆AGV的任务完成时间和延迟时间对比分析Fig. 4 Comparative analysis of task completion time and delay time with 9 AGVs
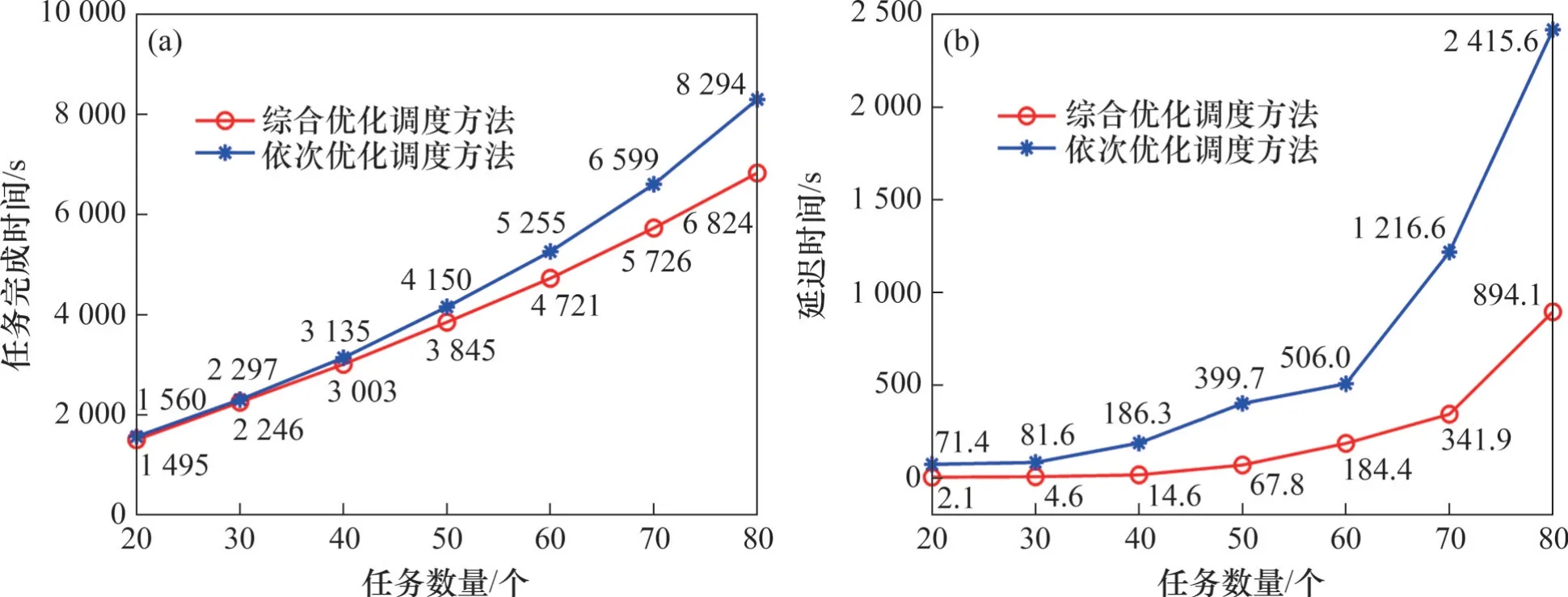
图5 使用15辆AGV的任务完成时间和延迟时间对比分析Fig. 5 Comparative analysis of task completion time and delay time with 15 AGVs
案例分析结果表明,本文所提出的综合优化调度方法具有更好的性能,在所有案例中都找到了更优的解。具体表现为:相较于依次优化调度方法,综合优化调度方法的任务完成时间缩短了10.56%,延迟时间减少了74.53%。值得注意的是,这2 种方法的延迟时间在任务数为20 时任务完成时间仅相差42.63 s,但当任务数增大到80 个时,其任务完成时间相差1 281.13 s。因此,随着任务规模增加,AGV 之间发生冲突的可能性也越大,依次优化调度方法不能从任务分配过程中规避碰撞冲突的影响,而综合优化调度方法可以通过改变任务分配和具体执行路径,规避大多数冲突情况。
为了进一步验证综合优化调度方法在大规模任务案例中减少碰撞冲突的作用,使用30辆AGV将2种方法在任务数分别为110~150个的案例中对碰撞冲突次数进行对比。每一个案例随机生成10组任务,每组运行10次程序取平均值,结果如图6所示。从图6可以得到:综合优化调度方法能大幅度减少AGV 之间的碰撞次数,与依次优化调度方法相比,平均碰撞次数降低73.3%。
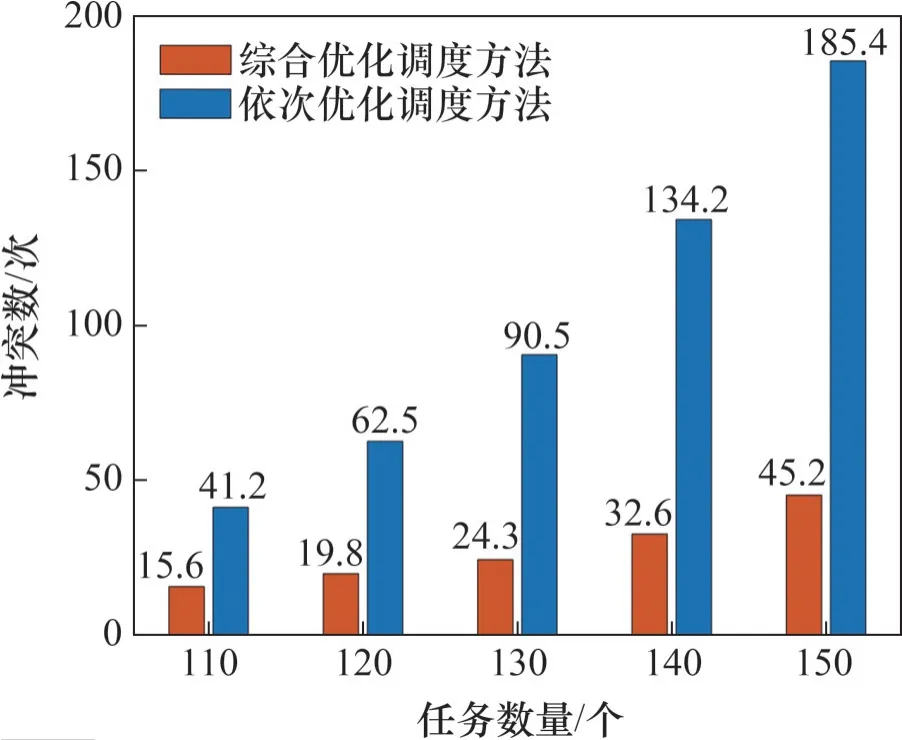
图6 平均碰撞次数对比分析Fig. 6 Analysis of conflicts number
3.2 对比验证分析
为了更全面地验证HDSTA 的性能,需要建立更大规模的案例范本。将20~100 个任务定义为小规模问题,待调度的AGV 从5 辆到15 辆不等;将100个任务以上定义为大规模问题,待调度的AGV从15辆到30辆不等。在对比实验中,对于不同规模的每个案例随机生成10 组任务,每组运行10次,共运行100次程序,对比任务完成的时间。在每个案例中,将HDSTA与自适应大邻域搜索算法(HALNS)[15]、预先规划算法(PPA)[13]和DS算法进行对比。其中,HALNS 是一种混合了自适应大邻域搜索算法和线性规划的算法,用于求解带电量约束的异构AGV 调度问题。但该方法没有考虑冲突和死锁问题,为了进行比较,对其最优解进行冲突检测并增加延迟时间。PPA是一种在路径规划过程生成无冲突最短路径的算法,本文将综合调度优化方法与无冲突路径策略进行比较。DS 是基于离散状态转移算法的综合求解方法,用于与本文提出的基于HDSTA的综合求解方法作对比。算法的计算时间同样是重要的性能指标,因此,设定算法最大计算时间为120 s,对比结果如表1和表2所示。
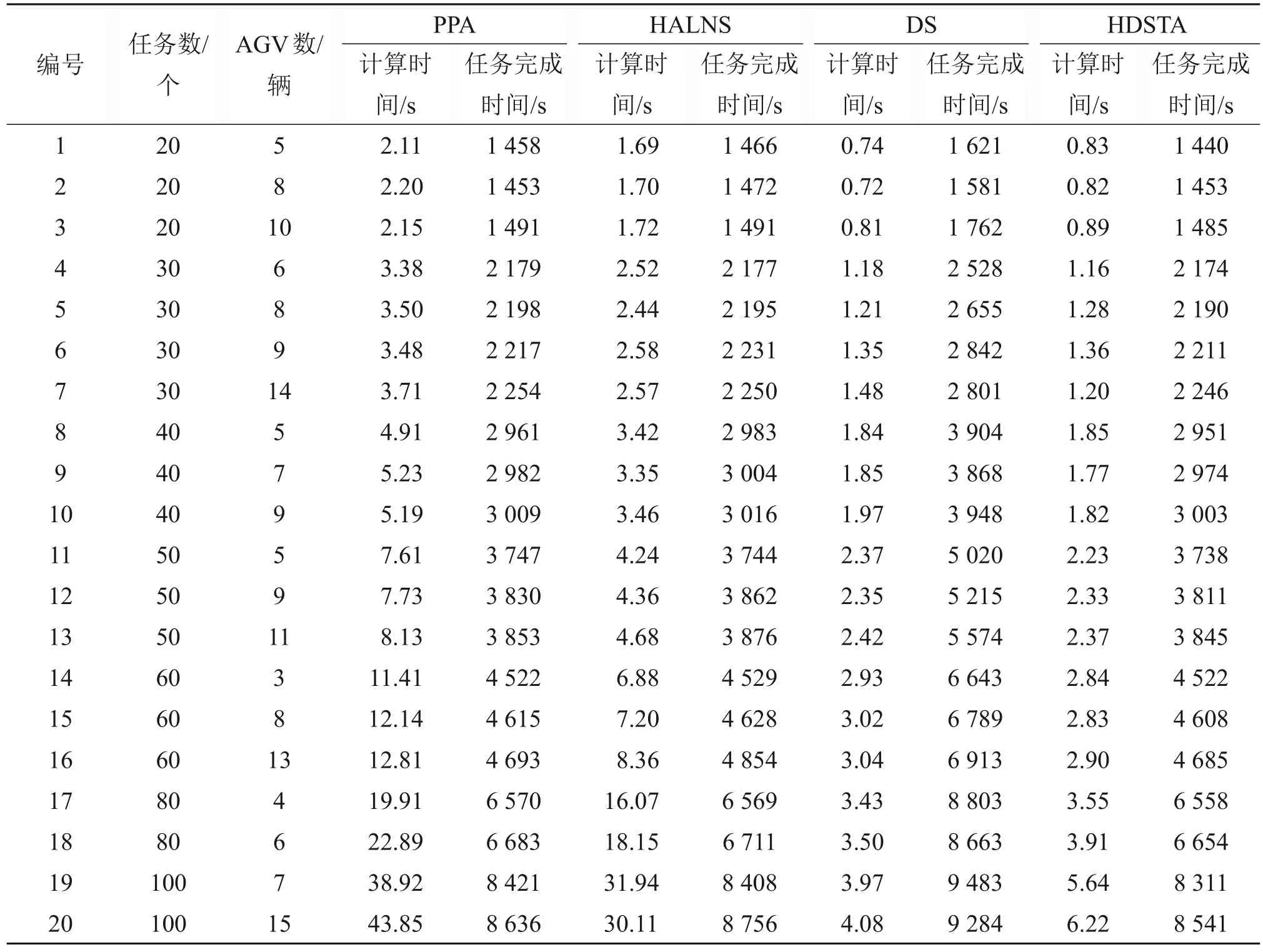
表1 小规模案例对比分析Table 1 Results for the small-scale instances
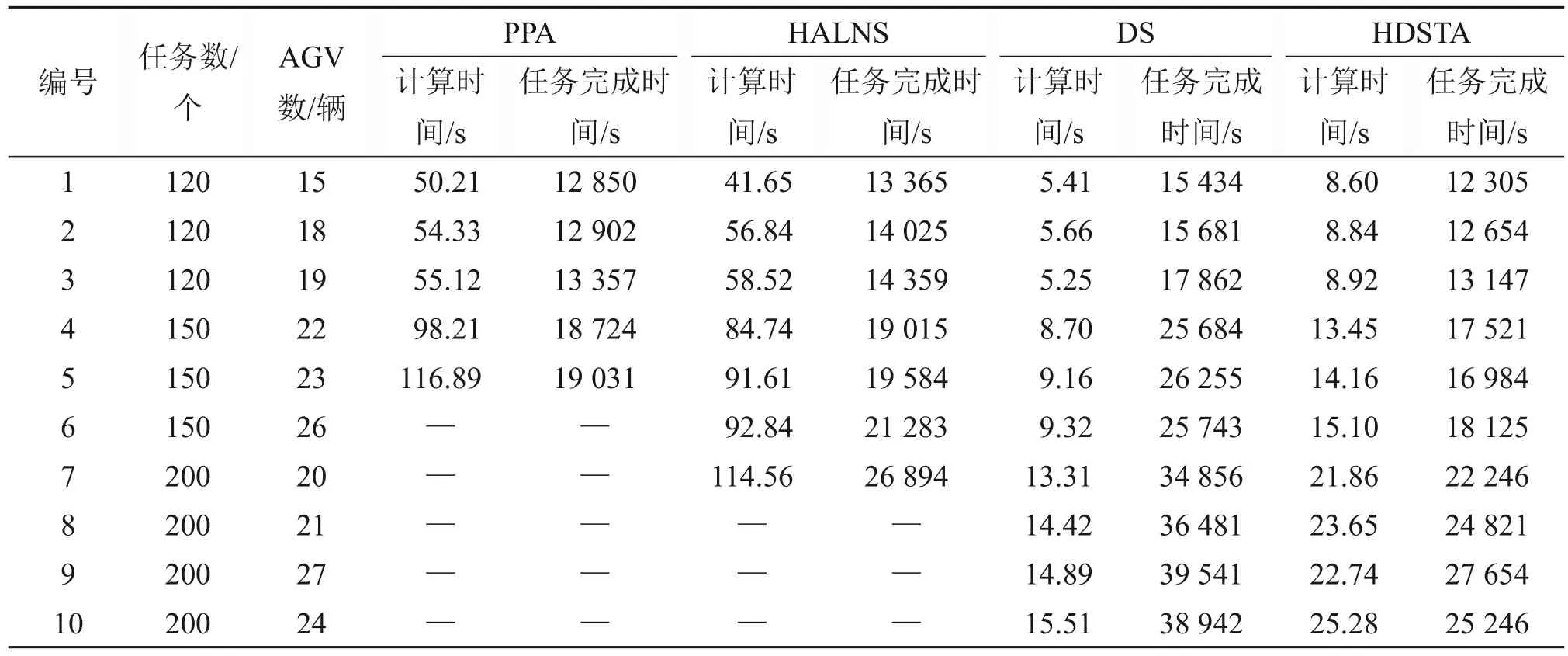
表2 大规模案例对比分析Table 2 Results for the large-scale instances
任务完成时间与运行成本成正比,可以直观反映AGV 协同运行效率,而计算时间是动态调度的重要指标,可以反映AGV系统的计算效率。从表1可见:当任务数量为20个,AGV数量分别为5,8和10辆时,采用HDSTA算法优化调度计算得出的方案任务完成时间分别为1 440、1 453 和1 485 s,计算时间分别为0.83、0.82 和0.89 s;通过20 个小规模案例类型的200组任务的结果分析发现,相较于PPA 和HALNS,本文提出的HDSTA 解的任务完成时间平均值分别缩短0.48%和1.16%,计算时间分别降低78.40%和69.74%。DS 求解时间与其他3 种综合调度方法相差较大;在小规模问题中,几种综合调度方法求解时间相差不大,而HDSTA的求解时间更少。从表2 可见:当任务数量为120个,AGV 数量分别为15、18 和19 辆时,采用HDSTA 算法优化调度计算后任务完成时间分别为12 305、12 654 和13 147 s,计算时间分别为8.60、8.84 和8.92 s;通过10 个大规模案例类型的100 组任务的结果分析发现,与PPA 和HALNS 相比,HDSTA 可以在更短的时间内求得质量更高的解,任务完成时间分别缩短5.54%和9.73%,计算时间分别降低86.68%和84.19%。在大部分案例中,DS不能得到整体最优的结果,HDSTA 虽然计算时间比DS的更长,但仍在一个合理的范围内。
4 结论
1) 本文提出的基于分层规划的综合优化调度方法比依次优化调度方法平均任务完成时间减少10.56%,碰撞冲突造成的延迟时间减少74.53%。
2) 在所有案例中,DS 都不能得到整体最优的结果。在100个任务内的小规模问题中,本文提出的方法比HALNS 和PPA 任务完成时间分别减少1.16% 和0.48%,计算时间分别减少69.74% 和78.40%。在100个任务以上的大规模问题中,本文提出的方法比HALNS和PPA任务完成时间分别减少9.73%和5.54%,计算时间分别减少84.19%和86.68%。

