基于改进自适应卡尔曼滤波的电力大负荷预测与计费研究

隋仕伟，俞海猛，蹇照民，赵 艳

（1.国电南瑞南京控制系统有限公司，南京 210000；2.国网新疆电力有限公司，乌鲁木齐 830000；3.南京工程学院 电力工程学院，南京 210000）

0 引言

电力是现代社会最不可或缺的能源资源，近年来国家社会经济的高速发展，导致了电力的需求量一直居高不下。电力公司负责电力供应的全过程，包括发电、输电、变电、配电等，才能将电力运输到客户端。每个地区的经济发展条件不同、人口数量不同、气候不同等都会影响对电力的消耗量，进而产生不同程度的电力负荷，这个过程是计划性的。因为通过负荷预测特别是大负荷预测，可以帮助电力公司提前确定未来的电力需求，提前做好电力规划，避免造成电力浪费或者不足的情况；根据预计负荷，电力公司还可以对从发电公司购买能源进行投资和决策，并规划维护和扩建。综上，提前预知电力负荷可以有效地保证电力系统的稳定运转，增加电力公司的营收。所以精准地提高负荷预测，微观上不仅有利于科学的安排电力调度计划，有利于提前安排电力系统运行方式和各种检修计划，还能够实现能源的节约，降低电网运行成本，宏观上有利于制定完备的电力系统建设规划，提高电力系统产生的经济效益和社会效益，助力我国未来要实现的 “碳达峰、碳中和”重要国家战略。所以电力负荷预测成为电气工程领域中的重要课题。

基于上述背景，本文提出了一种基于改进的AEKF 的电力大负荷计量计费预估方法，以期提高电力负荷预测准确性，为电力规划提供可靠的参考数据。

1 电力大负荷预测现状

目前的电力大负荷预估分为两种类型，一种是长期大负荷预测；一种是短期大负荷预测。长期大负荷预测可参考的数据众多且有规律可循，数据较为稳定，因此相关研究较为成熟，预测结果也较为准确。短期大负荷预测由于各种突发因素如天气、节假日等的影响，都会在一定程度上造成负荷波动，从而影响预测结果［1］。在此背景下，国内外专家和学者针对电力大负荷预测进行了深入研究。

1.1 长期预测

陈潇雅［2］等考虑电力系统规模大、辐射范围广和后期增设变压器等因素，提出最大限度的规划电力系统配置，来满足大负荷的发展。采用优化后的Elman神经网络，在传统的电力系统网络节点的基础上增加节点，考虑数据量大、控制函数溢出和收敛性弱等不足。通过联络有效度分析结果，验证了该系统的规划方案，并根据实例证明了该方法可以提出可靠的电力系统对于大负荷长期规划的方案。胡新文［3］针对大负荷长期预测的数据量不足和波动性大的问题，采用改进后的灰色模型进行求解，避免了时间序列预测的数据量大的难题，根据求解微分方程，假设每个样本的数据点都是约束函数，考虑电力大数据的不确定性带入优化模型。实例证明，该模型提高了长期负荷预测的精确度。李长庆［4］等采用两中方法对电力大数据的预处理，增强了电力系统大数据的原始性，并削除了一些异常值，通过傅里叶误差修正，效验了与真实数据的误差，针对长期预测的波动问题和剔除数据的问题，基于引用动态参数和适当增加目标函数年数据的权重，提出了误差修正的等维度动态参数预测模型，通过实例证明改方法模型的精确度高于大多数传统模型。黄元生［5］等提出了粒子群和高斯过程融合的电力系统负荷预测模型，采用粒子群算法对协方差进行修正，将优化后的参数带入到高斯过程，对该过程进行电力系统优化培训，修正后的模型和指滑模型进行对比，实例验证，该模型的精确度和稳定性更为优异。陈娟［6］等针对电力系统长期负荷预测的波动性强、误差大和随机性强的问题，采用了非线性的神经网络算法进行提高预测精确度，在预测的基础上结合人工神经网络的原理，为电力系统真实数据下的电力系统规划提供了理论依据。王凌谊［7］等提出了迁移学习的长期负荷预测以为了减少真实电力大数据不足对结果精确度造成的影响，综合考虑电力系统数据的该地区的社会经济问题的因素，扩大样本的迁移范围。实例验证，该模型能够有效提高电力负荷预测的精确度。

T.Hong［8］等为避免传统方法低分辨率数据导致的精确度低的问题，提出了一种根据每小时的动态数据预测方法，该方法具有更好的准确性和防御性。并且将长期预测的3个步骤现代化，跨场景分析新建模型，提出了负载归一化和天气归一化的负荷的模拟方法。实例证明，该方法得出的结果具有比传统模型具有更高的精度。J.P.Carvallo［9］针对长期公共事业负荷精确度进行分析，对美国西部12家电力负荷进回顾性分析，我们发现预测的准确性和预测技术的复杂性之间的关联性很弱。此外，执行的对负荷增长的敏感性和风险分析及其对能力发展的影响也没有做得很充分。研究了对公用事业负荷预测的调整。不准确的长期负荷预测方法所带来的政策影响。R.K.Agrawal［10］等为了解决传统方法的仿真数据来自于月季度和年进度的电力系统分析，导致准确度非常低，提出了长短期记忆细胞组成的递归神经网络为中心的模型，考虑时间序列数据内在关系。实例证明，该模型的平均百分比误差在6.54左右，具有较高的精度，另外该模型的运行时间为半个小时，有利于离线计算负荷预测。

综上，目前从电力系统大数据长期负荷预测的方法可以看出，大多数方法都是基于传统模型，然后通过进行参数优化、方法改进和多种求解算法进行融合等到目标求解模型。这些研究大致思路相同，并且这些方法大多没有加入程序中进行仿真，下一步的方向可以考虑在现代化软件中进行仿真验证，该模型的求解速度和收敛精确度。

1.2 短期预测

钟劲松［11］等基于用户负荷小、偶然性强的特点，根据深度学习理论和互信息融合，构建了长短期记忆网络和最大相关最小冗余的短期负荷预测模型，先根据排序特征变量，组成变量集合，带入到长短期记忆网络中去，最后通过算例验证了算法的有效性，避免了梯度消失和梯度爆炸的问题。白冰青［12］等提出了一种新型城市与新能源结合的多种类型负荷结合的短期负荷预测模型，采用序列到序列和双重机制融合，兼并采用最小冗余最大相关性的方法，进行求解目标函数，算例证明，该方法具有更好的鲁棒性和精确度。尹春杰［13］等通过温度、天气和历史数据多个控制变量，采用循环神经网络下的微电网负荷预测模型。实例验证，与多种神经网络下的算法结果对比，该微电网负荷预测模型优于其他模型。王荣茂［14］等为了解决传统台区逻辑归一化的问题，构建了基于长短记忆神经网络的经验模态分解的负荷预测模型，采用历史数据进行验证证明，该方法具有较强的鲁棒性和收敛性。钟光耀［15］等为了避免计算资源消耗过大，首先进行概率归一化，构建相似度判断依据和训练集，得到目标模型，使用某市级配电网数据验证，该模型准确率提高了2.75%和计算速度提高了约6倍。赵允文［16］等为了解决负荷预测时间长和准确性低的问题，提出了随机配置网络和相空间重构融合预测模型，使用住院分析法进行降维，通过互信息法和虚假近邻法求取参数并重构相空间，最后使用随机配置网络预测电力负荷，采用欧洲公开数据验证证明，改方法具有智能化和高精度的特点。S.H.Rafi［17］等构建了一种新型负荷预测方法，该方法基于长短期记忆网络和卷积神经网络融合，克服了传统低精度的困难，该方法在孟加拉国电力系统进行验证，验证了该方法的有效性，证明了该方法有着较高的精确度和准确性。文献［18］提出考虑温度、湿度和风速等外环境引起电力负荷变化的因素，采用长短期记忆网络求解目标函数，对多个时间周期进行验证，证明了该预测方法的预测精度高于传统方法。L.F.Yin［19］等设计了一种多时间空间尺度时间卷积网络进行短期负荷预测，考虑了负荷数据的学习非线性特征和时间序列特征，并且进行了多个时间长度进行验证，和22种人工智能算法进行对比，仿真结果证明该算法具有较高的精度。K.J.Chen［20］等构建了深度剩余网络预测模型，通过整合领域知识，对结果进行深残差网络验证，使用3 个公共网络数据进行验证了该模型的有效性。

综上，短期负荷预测是电力系统对电能生产、输送和调度的保证，根据方案进行合理的安排。目前短期负荷预测的精度研究技术大多集中在了传统方法、经典算法和人工智能算法，根据这些方法可以对不同地区进行选取合理的预测方法，对以后短期负荷的更高的精度和收敛性的预测提供理论基础。

目前电力大负荷预测研究较多，也比较成熟，目前最为适用和成熟的预测方法是卡尔曼滤波方法，他的优点是适应性好、抗干扰能力强，缺点是以调度计划为唯一目的，未考虑计量计费因素，因此提出一种改进的AEKF 的电力大负荷计量计费预估方法势在必行。

2 AEKF负荷预测

2.1 传统EKF预测

卡尔曼滤波（KF，Kalman filtering）的基本原理是通过前一时刻的历史数据来预估下一时刻的数据并进行修正［21］。具体过程如下：

1）设置初始参数。

2）利用系统状态预测方程计算t＋1时刻电力负荷预测值，方程表达式如下：

式中，St代表t时刻电力负荷预测结果；α代表状态转移矩阵；St-1代表t-1 时刻的最优估计值；β代表系统模型参数；Et代表t时刻系统的控制量；Ft代表t时刻的过程噪声。

3）计算卡尔曼估计误差协方差Rt，并组成协方差矩阵R。

4）计算卡尔曼增益。计算公式如下：

式中，Gt代表t时刻卡尔曼增益；Q代表测量系统的参数；U代表量测噪音方差。

5）对卡尔曼估计误差协方差Rt进行校正，校正公式如下：

式中，R1t代表校正后的电力负荷协方差；I代表单位矩阵。

6）算得出校正后的现在时刻的最优化电力负荷预测值S1t。

7）重复上述过程，直至得到最后时刻的电力负荷预测值，完成预测。

从上述步骤可以看出，KF在进行预测之前，需要对电力大负荷历史数据进行预处理，后续的计算都是基于预处理结果的，如果预处理效果不佳，其中存在的噪声数据会严重干扰后期预测结果。实际工程案例中，常常出现因为历史数据进行预处理结果不佳，导致预测结果完全偏离真实值的状况［22］。

同理，在KF预测过程中，误差协方差Rt通过离线测量实验确定以及β、Q等参数也是预测的重要计算影响因素，其值的确定非常重要，实际工程案例中，往往按照经验设定或者通过仿真过程调整来设定误差协方差Rt以及β、Q等参数，这些参数设定后就固定不变，缺乏自适应性，若出现感染，则会导致预测结果与实际结果存在较大的偏差［23］。

2.2 改进的AKF预测方法

针对2.1中所述，提出一种改进的自适应卡尔曼滤波（AKF，adaptive Kalman filter）的电力大负荷预测方法。其改进主要针对数据预处理改进、增设自适应环节、误差协方差Rt以及β、Q等参数整定改进3个环节。

2.2.1 数据预处理改进

预处理改进包括3个方面：缺失数据填补、异常值检测与处理以及标准化处理。

1）缺失数据填补：由于历史负荷数据具有很强的时间序列性，因此当缺失一个数据的时候，可以通过计算前后时刻的均值来进行填补。设计填补数据计算公式如下：

式（5）中，at代表t时刻缺失的数据；at-1、at＋1代表缺失数据前一时刻和后一时刻的电力负荷数据。

考虑到工程实践中，因为网络中断、设备故障等情况导致缺失的历史数据较多的情况也存在，设计下述公式：

式中，at＋n代表t时刻缺失数据后的t＋n时刻的电力负荷数据；n代表时间差值；代表电力负荷数据平均值。

2）异常值检测与处理：异常值是指偏离真实值的异常数据，主要分为两类，即毛刺数据和极值数据。

毛刺数据预处理方法如下：先利用公式（7）进行判别：

式中，bt、bt＋1分别代表t时刻和t＋1时刻的电力负荷数据；△b代表设置的允许误差阈值。当bt和bt＋1之间的误差绝对值大于等于△b，则认为bt为毛刺数据，剔除之后，利用式（6）填补上。

极值数据预处理方法如下：设bt为待检测t时刻电力负荷数据，首先找出同类型日期同一时刻点负荷数据并组成序列，记为数列b1，b1…bm。计算该序…列的均值和标准差，记为b、b，然后计算偏离率，计算公式如下：

式（8）中，D代表偏离率。当D大于等于设定的偏离阈值△D，认为bt为极值数据，剔除之后，利用式（6）填补上。

3）数据标准化：为提高后期预测模型的收敛速度，增加数据标准化环节，设置标准化公式如下：

式中，C1t、Ct代表t时刻标准化后、前的电力负荷数据；Cmin、Cmax代表电力负荷数据最小值和最大值。

2.2.2 增设自适应环节

在传统KF的基础上引入自适应遗忘因子λt，从而增强对电力负荷预测数据的抗干扰能力，实现自适应性，提高预测的准确性。

自适应遗忘因子λt计算公式如下：

式中，Ut代表t时刻量测噪音方差矩阵；ht代表t时刻过程噪声方差；Ht代表t时刻噪声误差方差；Lt代表t时刻的卡尔曼估计误差增益因子；Rt-1代表t-1 时刻的卡尔曼估计误差协方差；δt代表t时刻的新息；ω代表卡尔曼滤波器的记忆长度。

将上述计算出来的自适应遗忘因子λt引入公式（4），即得到最优化电力负荷预测模型如下：

式（14）中，S1t代表改进后的电力负荷预测值。

增设AKF环节后的算法的流程如下：

由图1可知，增设AKF环节后的基本步骤为：设置初始参数，根据系统状态方程建立电力负荷观测方程；利用传统卡尔曼滤波算法进行卡尔曼估计误差协方差与卡尔曼增益的计算，并校正卡尔曼估计误差协方差，以完成状态量估计，然后引入自适应遗忘因子，修正系统状态噪声协方差阵，输入改进后的电力负荷预测模型公式，输出电力负荷预测结果。

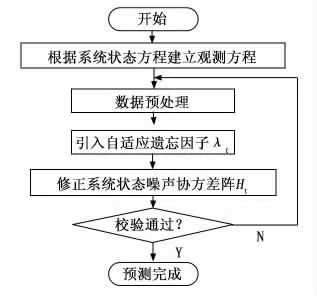
图1 算法流程图

上诉流程中的重要参数自适应遗忘因子λt由公式（10）确定，修正系统状态噪声协方差阵Ht由公式（11）确定。2.2.3 关键参数整定

在上述步骤2.2.1 研究中，数据预处理改进提高收敛速度，2.2.2研究中，是假设电力负荷数据较为理想平滑的。但是受到温度、日期等其他因素的影响，异常值处理时往往会将波动较大的正常电力负荷数据认为是异常数据将其剔除，继而影响误差协方差Rt以及β、Q等参数的整定，这显然是错误的。

为了弥补这个缺陷，引入参数整定因子的概念，具体实现方法如下：首先收集异常值检测与处理步骤中剔除下来的认为是异常的数值，计算这些数值的均值，公式如下：

式（15）中，X代表剔除后的历史电力负荷数据均值；xi代表剔除后的第i个历史电力负荷；M代表剔除后的数据数量。

然后计算剔除后的剩余的正确的历史电力负荷数据的均值，记为Y，得出整定因子Υ，即：

对改进自适应卡尔曼滤波算法得出的结果进行整定，如下：

式中，△St代表整定后的电力负荷预测结果。

由于是以标准化后的历史电力负荷值得出的预测结果，因此还需要将其进行反标准化，才能得到实际负荷预测值△S1t。反标准化如下：

最终根据△S2t得到电力大负荷计量计算公式为

式中，Ψ代表电力计量值；k代表电能利用率；△t代表时间；η代表线损。

计费公式：

式中，μ代表电费；ωt代表t时刻的单位电力价格。

至此，电力大负荷预测与计量过程结束。除上述过程外，其余预测过程与传统KF电力负荷预测过程一致。

3 仿真分析与应用

3.1 数据样本

以江苏省南京市江宁区2022年5月20日的电力大负荷为研究对象。获取2018，2019，2020，2021年5月20日的电力负荷数据作为样本如图2所示：

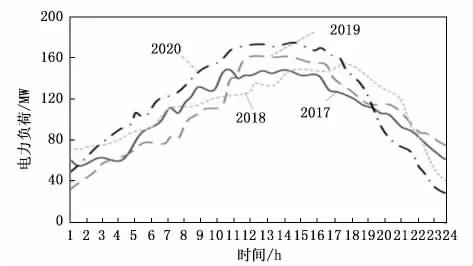
图2 大负荷样本数据

3.2 仿真结果

在Matlab2016a仿真平台，以基于改进的AKF 的电力大负荷预测方法作为对比结果。选择3种对比方法：基于变分模态分解（VMD，variational modal decomposition）和时间卷积网络（TCN，time convolution network）预测方法、基于互补集合经验模态分解（CEEMD，complementary set empirical mode decomposition）和最小二乘支持向量机（LSSVM，least squares support vector machine）的预测方法、基于灰色关联长短期记忆（LSTM，long short-term memory）的预测方法作为参照对比系，得到电力大负荷预测结果如图3所示。

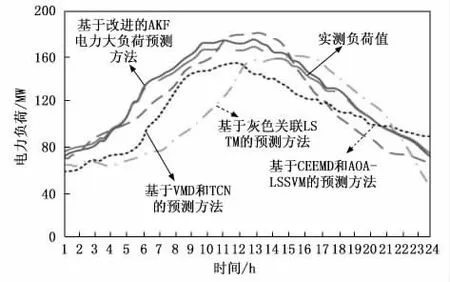
图3 预测结果

根据图3和公式（20）进行计量计费，结果如图4所示。

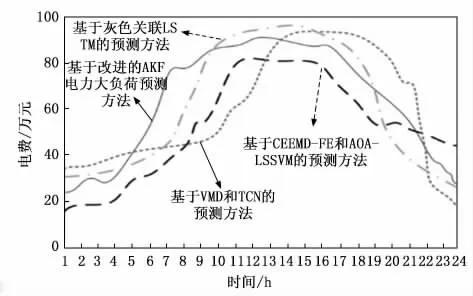
图4 电力计费结果

3.3 结果分析

1）观察图3，明显可见基于改进的AKF的电力大负荷预测方法的预测结果和真实负荷更为接近，两者曲线重合度较高；

2）计算图3中几种预测方法的预测数据与实际负荷数据之间的误差MAPE，算式如下：

式（21）中，n代表样本数量，xi代表预测负荷数据，x代表实际负荷数据。

从表1中可得出：基于改进的AKF的电力大负荷预测方法应用下，电力负荷数据预测结果与实际结果之间的平均绝对百分比误差更小，不同时刻下的平均绝对百分比误差的平均值小于1.35%。基于VMD 和TCN 的预测方法不同时刻下的平均绝对百分比误差的平均值为2.398%；基于CEEMD-FE和AOA-LSSVM 的预测方法不同时刻下的平均绝对百分比误差的平均值为2.935%；基于灰色关联LSTM的预测方法不同时刻下的平均绝对百分比误差的平均值为3.455%，显然于改进的AKF 的电力大负荷预测方法的预测精度相对更高。

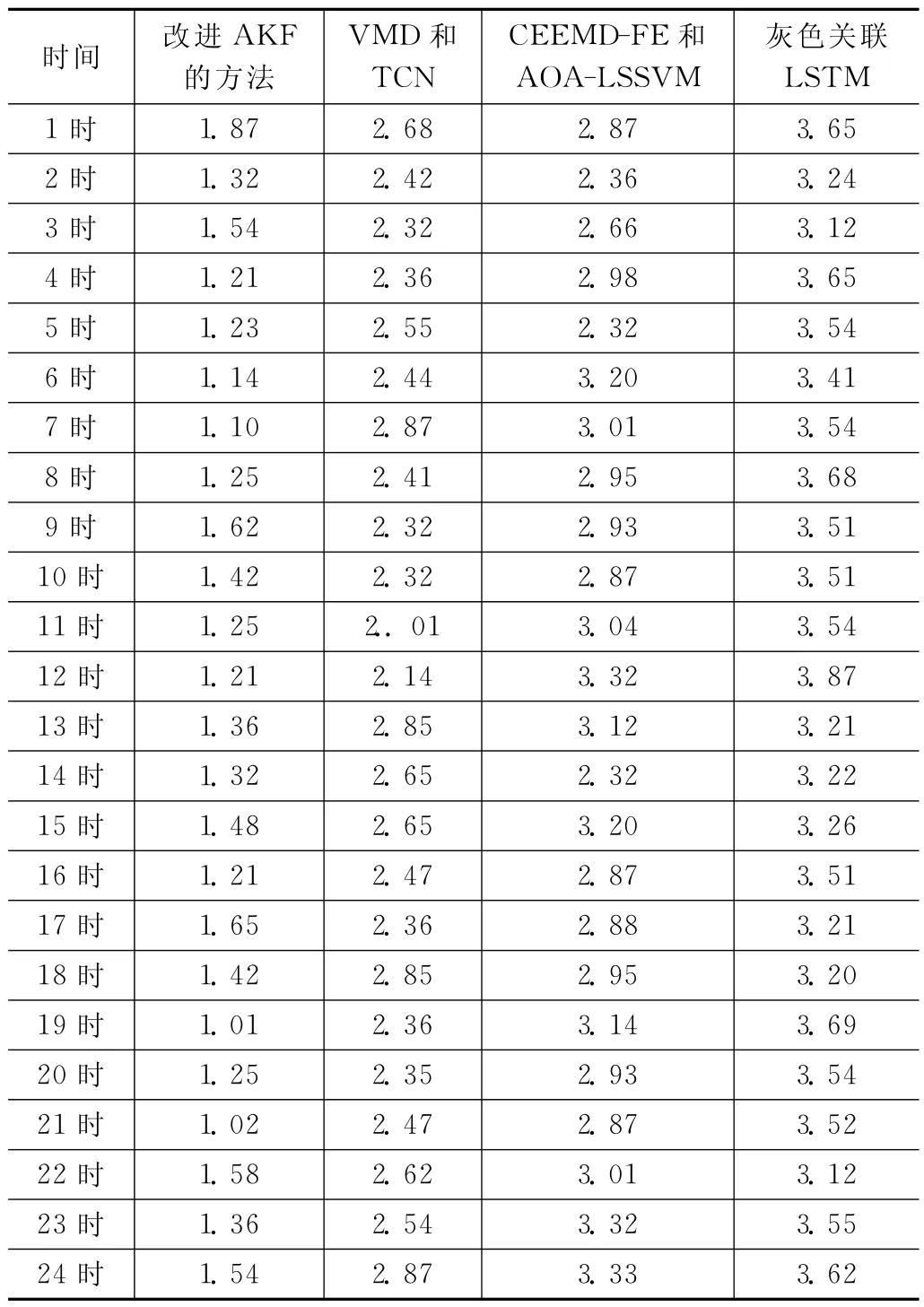
表1 不同方法电力负荷预测的误差 %

3）用相对百分误差（RPE，relative percentage error）来代表预测电费的准确程度，算式如下：

式（22）中，xi代表预测负荷数据，x代表实际负荷数据。相对百分误差值越小，意味着模型预测的精度越高。

计算图4中几种电力负荷预测方法各时刻的相对百分误差结果如表2所示。

表2 不同方法电力计费预测RPE %

表2显示：基于改进的AKF的电力大负荷预测方法各时刻下电力计量预测的平均绝对百分比误差的平均值为1.263%；基于VMD和TCN 的预测方法各时刻下电力计量预测的平均绝对百分比误差的平均值为2.184%；基于CEEMD-FE和AOA-LSSVM 的预测方法各时刻下电力计量预测的平均绝对百分比误差的平均值为3.017%；基于灰色关联LSTM 的预测方法各时刻下的平均绝对百分比误差的平均值为3.392%。同理，经计算得到，基于改进的AKF的电力大负荷预测方法各时刻下电力计费预测的平均绝对百分比误差的平均值为1.53%，而其他3种方法在各时刻下的电力计费预测的平均绝对百分比误差的平均值分别为2.537%、3.164%与3.659%。

可见在电力计费的精准预测上，基于改进的AKF的电力大负荷预测方法的预测结果是相对最接近实际值的。

4 应用案例

4.1 案例简介

本研究已经在国家电网江苏省电力公司投入使用，2022年8月下旬，我国遭遇了加大规模的电力能源短缺，基于本研究的负荷预测系统在电力调度和销售的实际使用中发挥了较好的效果。

具体应用如下：取江苏省南京市江宁区2018，2019，2020，2021年8月30日的每日24小时的居民生活用电电力负荷、电力计量与电力计费作为历史数据，并对其进行数据预处理，然后利用本文方法建立预测模型，整定模型关键参数，取得数据样本总数1 000个，剔除9个异常数据后剩余正常影子991 个，根据式（16），整定因子Υ 为0.991。对江苏省南京市江宁区2022年8月30日24小时各时刻的电力负荷、电力计量与电力计费结果进行预测，并与当日实际数据进行对比，结果如图5、图6所示。

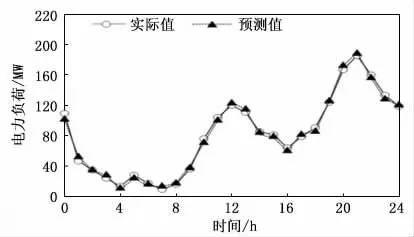
图5 电力负荷预测值与实际值对比结果

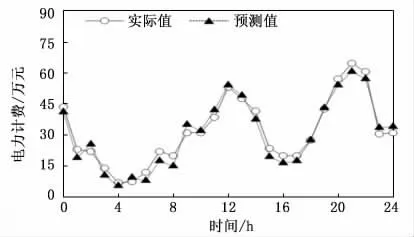
图6 电力计费预测值与实际值对比结果

4.2 效果分析

对应用案例获得的预测结果进行分析，从图6可以看出：由于引入了自适应遗忘因子λt，改进了传统的KF算法，以及引入参数整定因子Υ，使得模型预测更为准确，因此，实际负荷值与预测负荷值之间的拟合程度较好，预测结果精准地代表了真实电力负荷的变化趋势。

对应用案例获得的预测结果进行分析，从图6可以看出：电力计量与电力计费的走向预测同样较为准确。根据国网江苏省南京市公司的相关数据：能够提高电力公司的调度效率12%，增加电费营收5.3%～12.2%［24］。

5 结束语

5.1 结论

1）在电网的运行与调度过程当中，对电力负荷的预测起着非常重要的作用。精准的电力负荷预测既有利于提高电力系统的运行稳定性与可靠性，又能够降低电网运行的成本。只有精准的预测电力负荷，才能更精准有效地对电力计量与电力计费展开预估。

2）基于改进的AKF 的电力大负荷预测方法能够解决传统KF算法在预测过程中缺乏自适应性，从而导致预测结果与实际结果存在较大偏差的问题，引入自适应遗忘因子来改进KF算法的预测精度，效果明显。

3）对预测历史数据进行预处理：缺失数据填补、异常值检测与处理以及标准化处理，能够大幅度地提高预测的精度。但是受到温度、日期等其他因素的影响，异常值处理时往往会将波动较大的正常电力负荷数据认为是异常数据将其剔除，这在预测算法的设计中要予以注意，需要通过其他的方法进行修正。

4）在传统KF的基础上引入自适应遗忘因子λt，增设自适应环节，可以增强对电力负荷预测数据的抗干扰能力，提高预测准确性。

5）误差协方差Rt以及β、Q等参数的整定对预测精度的影响很大，提高他们的准确度，可以到幅度调高预测精度。

6）仿真实验数据表明：基于AEKF的电力大负荷计量预测方法的负荷预测结果与实际结果误差小于1.35%，电力计费预测结果与实际结果相对误差小于1.263%。优于VMD和TCN 预测方法、CEEMD-FE 和AOA-LSSVM 预测方法、灰色关联LSTM 预测方法等对比系。

7）工程应用案例表明：基于改进的AKF的电力大负荷预测方法无论是负荷预测还是计费预测，实际值与预测值的拟合效果都较好，能够提高电力公司的调度效率12%，增加电费营收5.3%～12.2%。基于改进的AKF的电力大负荷预测方法可靠度较高，具有很好的实际应用价值。

5.2 展望

因为每天同一时刻的实测电力负荷序列本质是具有平稳过程的时间序列，所以在未来的研究中，可以考虑建立时间序列模型，将噪声视为均值为零并且互不相关的白噪声，将每天同一时刻的实测电力负荷序列也作为历史数据输入，以期实现抗干扰能力强、精准度更高的预测。