基于海洋气象漂流浮标的动态测风技术研究
薛帅宁,孔卫奇
(1.重庆市气象信息与技术保障中心,重庆 401147;2.成都市气象局,成都 611133)
0 引言
海洋风是海洋学和气象学观测中的基本要素参数,更是人类在海洋开发过程中必须参考的要素之一[1]。海上风灾难事故频发,根据之前的中国渔船安全分析统计研究表明,1999~2005年各类海上事故导致渔船损失704艘,其中风灾害事故就占据了其中的51.85%。由此可见,风灾害是导致渔船安全事故发生的主要原因,对海洋风的观测愈发显得重要[2]。通常所说的测风为陆地平面测风,对于海洋环境下风的观测,由于海面海浪、湍流等各种不稳定因素影响,使得在海上动态环境下的测风技术难度增大,测量结果误差较大。目前较多的有利用无人机携带传感器、多普勒激光雷达、船舶等进行海洋风数据观测[3-5]。随着卫星跟踪、定位和通信技术的不断发展,越来越多的卫星跟踪浮标被用以开展海洋观测[6]。海洋气象漂流浮标是集海洋水文要素和气象要素为一体的、具有完全自主知识产权的国产海洋气象观测设备,具有观测要素多、经济性、可抛弃性等优点。基于海洋气象漂流浮标上的测风技术是指搭载于海洋气象漂流浮标上的测风传感器在姿态动态变化条件下的测风技术。海洋气象漂流浮标长期工作在海面上,受海况影响,浮标体运动姿态不断变化,导致测风传感器倾斜角度也不断发生着变化,测量误差较大。因此在进行海面风要素测量时,对漂流浮标实时姿态数据进行观测很有必要。利用漂流浮标实时姿态变化数据,得出传感器的倾斜角度,对漂流浮标上搭载的测风传感器测得的风速风向数据进行质量控制和误差补偿,使所得数据满足气象观测业务的需要。
传统的测风方法包括机械式、热线式、激光多普勒式等[7]。机械式测风虽较为普遍,且价格低廉,但是不符合复杂海况条件下的观测环境;热线式测风具有易携带、灵敏度高等优点,但更多用于矿洞等狭窄空间中[8];激光多普勒式测风仪具有响应快速、精度高的优点,但是需要人工掺入粒子作为散射中心,并且价格昂贵[9]。超声波测风传感器具有精度高、稳定性强、能适应复杂的观测环境等优势,较为适合用来在动态环境下的风速风向测量[10-11]。结合复杂海况的测量条件和经济成本,本文选取了FT742-SM 型超声波测风传感器,它采用声共振技术(acoustic resonance),体积小,可补偿温度、气压和湿度所带来的测量误差。采用固态一体化设计,无活动零部件,无需重新标定,且采用硬质阳极氧化铝外壳,具有极强的抗物理冲击性和极高的抗盐雾腐蚀能力,是专门为恶劣环境下测风技术设计的,符合此次海洋气象漂流浮标测风的技术要求。
1 传感器倾角解算
本文漂流浮标姿态信息的测量采用基于陀螺仪、加速度计和磁力计九轴测姿技术的MPU9050传感器,根据它测量出的四元数数据q0,q1,q2,q3进行三个姿态角的解算。为便于计算,本文选用欧拉角内旋转模型,即绕载体自身三个坐标轴的三次旋转的复合作用,各种不同的旋转顺序只要满足任意两个连续旋转必须绕着不同的两个旋转轴旋转的原则,即可对同一时刻载体的姿态进行正确的描述[12]。本文选用的旋转顺序为Z-X-Y,也称为 “航空次序欧拉角”,旋转过程如图1所示。

图1 欧拉角旋转示意图
其中:Oxbybzb为载体坐标系,Oxnynzn为地理坐标系。定义绕X轴旋转角度称为横滚角roll,用字母γ表示,取值范围为±180°;绕Y轴旋转称为俯仰角pitch,用字母θ表示,取值范围为±90°;绕Z轴旋转称为航向角yaw,用φ表示,取值范围为:0~360°,各个旋转正方向满足右手定则[13]。
欧拉角模型可以十分形象地表述出载体姿态角在三轴空间中的变化,因此最终的姿态解算结果都用欧拉角作为显式。但是在基于角速度传感器的姿态解算过程中,欧拉角法存在三角函数计算问题及方程的奇异现象[14-16],而四元数法不仅不会出现方程更新的奇异现象,而且易于计算。所以,具体的姿态解算过程一般转化为四元数法进行计算[17]。四元数解算模型的基本思路是:定义一个绕参考坐标系的矢量通过单次转动可实现两个坐标系之间的转换,表达式如下:
式(1)中,i、j、k是虚数,a是实数。其中三个虚数i、j、k满足:
根据Euler定理和姿态四元数的“轴角”表示方法,可设一空间向量n等效载体旋转方向,由向量n和载体转动角度θ可构造四元数来表示载体坐标方位。这样就可以用范数将载体所处的三维空间与四维空间联系起来,然后通过规范化后的四元数来描述三维空间的旋转。得到式(1)的最简形式[18]:
其中:Q为单位旋转四元数,Q*为Q的共轭,利用方向余弦矩阵作为转换桥梁,展开后可得方向余弦矩阵和四元数的关系转换表达式:
再对同一姿态不同的表达方式进行转换,即可得到欧拉角的四元数表达式:
2 实验平台搭建
此次动态环境下测风的实验目的在于模拟海洋动态环境,对传感器姿态无规则变化下的动态测风进行数据测量和误差补偿,得到更加准确的风速风向值,为实际海况下海洋气象漂流浮标上的测风技术研究打下基础。实验过程中,将测姿模块与超声波测风传感器同轴安装,固定于风洞工作段中的垂直托盘上,随机晃动托盘改变传感器姿态,以秒数据同时接收实时风速风向数据和传感器姿态数据,对比风洞风速风向标准值,对传感器动态测风数据误差进行补偿。
为方便多次测量,本文动态测风实验在ZOGLAB(佐格)小型风洞中进行,测量过程如图2所示,该风洞能够提供最大20m/s的测试环境。风速测量标准器为ZOGLAB(佐格)计量DPM2500精密压差计,支持压差测风,风速数据可直观显示,实物图如图3所示,风向标准数据以超声波测风传感器自身无倾角状态下所测多组风向取均值作为标准值。

图2 动态测风实验示意图

图3 佐格计量DPM2500精密压差计
3 实验结果与分析
3.1 实验步骤和方法
1)实验设备安装。将超声波测风传感器与姿态测量模块同轴安装于实验风洞测试段下方的托盘上,可随托盘一体随机转动。
2)实验风场风速设置。选择5m/s、10m/s、15m/s、20m/s四种风速测试环境进行实验。
3)测试数据的采集、处理与分析。随机晃动托盘动态地测量各种倾角下的风速风向数据和姿态变化数据,等风速风向测量数据稳定后,连续读取8组数据和同时刻风洞风速风向标准值(其中测试数据均取 “秒”数据),求出测量误差,并对其进行处理和分析,以便后续的误差补偿算法研究。
3.2 实验数据处理分析
4种风速测试环境下姿态倾角值、超声波风速风向测量值、风洞对比风速风向值以及误差值分析如表1~4所示。
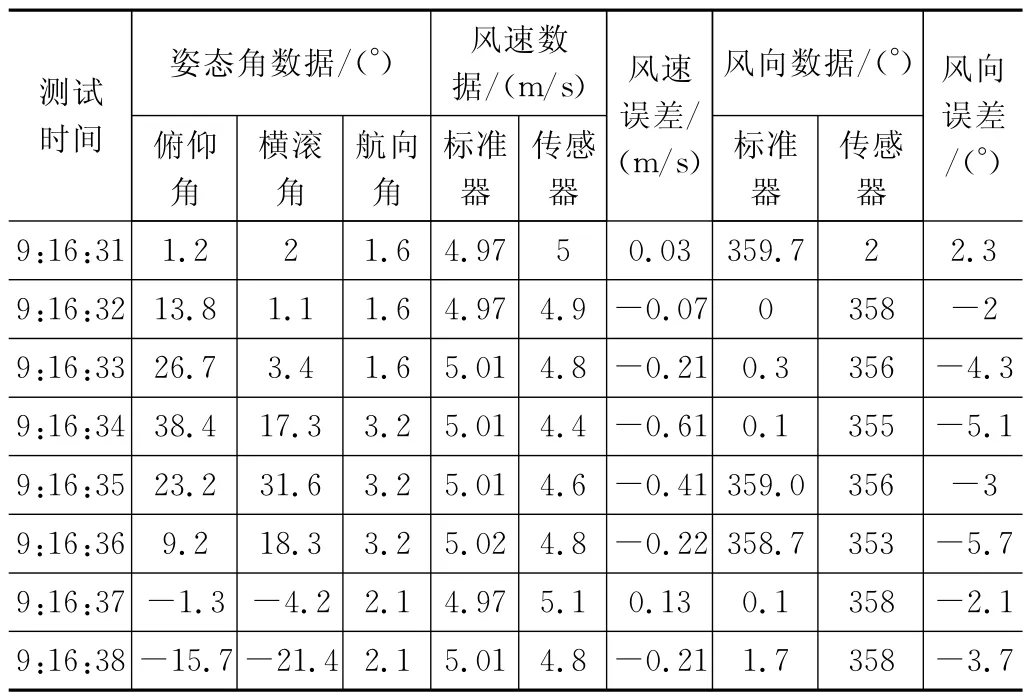
表1 5m/s风洞风速下的测量数据及误差
由表1可知,风速测量误差区间为-0.61~0.13m/s,风向测量误差区间为:-5.7~2.3°。
由表2可知,风速测量误差区间为-1.17~0.33m/s,风向测量误差区间为:-8.1~-3°。

表2 10m/s风洞风速下的测量数据及误差
由表3可知,风速测量误差区间为-1.56m/s~0.09m/s,风向测量误差区间为:-9.7~-0.5°。

表3 15m/s风洞风速下的测量数据及误差
由表4可知风速测量误差值区间为-2.42~-0.31m/s,风向测量误差值区间为:-10.7~7.8°。但是,实验过程中当风洞风速设为20 m/s时,风速数据有突变,后经工作人员验证,该实验风洞由于电机功率问题,风洞风速在超过18m/s时不稳定,数据可靠性得不到保证,因此不再对20m/s风速下的测量数据进行分析研究。
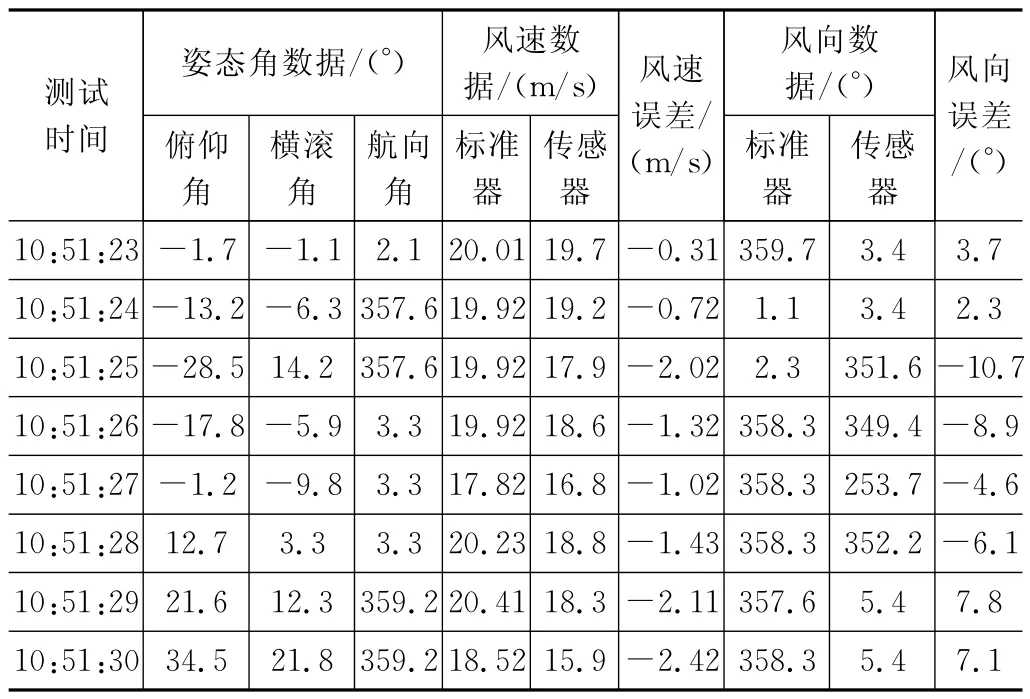
表4 20m/s风洞风速下的测量数据及误差
对表1~4 中动态测风数据误差结果进行处理分析可知:
1)随着风洞风速逐渐增大,测风误差随之增大,符合FT742-SM 型超声波测风传感器测量规律;
2)在倾角动态变化过程中,风数据测量不仅受到倾角变化还受到倾角变化速度等因素的影响;
3)风速测量值随传感器倾角增大特别是俯仰角的增大而增大,横滚角的变化对其影响则不是很大,特别是前后倾斜角度对其影响较大(传感器自身有遮挡),并且动态风速测量误差超过标准值10%,因此需要对动态风速测量误差进行补偿;
4)风向测量误差范围在±10°以内,误差较小,但仍可对其进行误差补偿,以求测得更加精确的风向值。
3.3 动态测风数据误差补偿
3.3.1 风速测量数据误差补偿
结合前文对动态测风误差影响因素的分析,将载体的线速度、角速度变化所带来的测量误差综合考虑为传感器姿态角的实时动态变化所带来的测量误差。由3.2节实验数据分析结果可知测量模块的俯仰角θ和横滚角γ两个因素对风速测量影响较大。因此,提出使用多变量拟合的方法,通过实验中测得的多组动态倾角下的风速测量数据与风洞风速标准值进行对比,可得到测量误差与俯仰角θ和横滚角γ的高次多项式,从而得到误差与这两个变量的关系,对所测量的风速数据进行误差补偿[19-20]。
运用多变量数据拟合的方法,可得:
式中,V表示标准风速值,Vc表示在对应横滚角和俯仰角下的风速值,ΔV为误差值;其中多项式的项数为lmax=;Pl为系数;(m+n)为多项式最高项,应用有限元法离散出K组数据l(1),l(2),l(3),…,l(k),相应地为俯仰角θ和横滚角γ标上上标,将每组数据代入式(12)中,可以得到如下方程组:
其中:C和ΔV已知,P未知,该式属于超定方程组(k>lmax),解不存在[21-22]。但可以找到一个特定的P,使得等号两端的差值达到最小,这个差值可写为:
利用最小二乘法求出其最小二乘解,使其总的平方误差达到最小[23-24]。求出式(13)的解[P0P1P2…PlmaxT,代入式(12)可得到多变量拟合表达式。得到风速测量误差与俯仰角θ和横滚角γ之间的关系,从而对动态测风结果进行误差补偿。
在使用式(12)对误差进行拟合处理时,选择m=n=2,可得:
选取所测风洞风速为10m/s的实验数据进行多变量拟合误差补偿,根据所测得的风速数据误差值与对应的俯仰角θ和横滚角γ值代入式(16),可求出误差补偿多项式的系数为:
将式(17)所得系数代入式(12)可得到风速多变量拟合表达式,经过误差补偿后的结果如表5所示。

表5 10m/s风速下误差补偿结果 m/s
经过误差补偿后,风速测量误差结果区间为:-0.77~0.13m/s,相较于补偿前误差结果得到明显改善。同样地,分别对5m/s和15m/s风速下测量误差进行补偿。
选取风洞风速为5m/s的测试数据进行多变量拟合误差补偿,根据所测得的风速数据误差值与对应的俯仰角θ和横滚角γ倾斜角度代入式(16),可求出误差补偿多项式的系数为:
将式(18)所得系数代入式(12)可得到风速多变量拟合表达式,经过误差补偿后的结果如表6和图5所示。

表6 5m/s风速下误差补偿结果 m/s
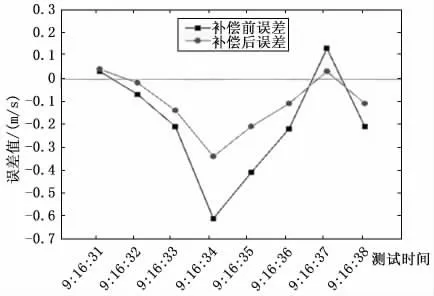
图5 5m/s风速下误差补偿结果
经过误差补偿后,风速测量误差结果区间为:-0.34~0.04m/s,相较于补偿前误差结果得到明显改善。
同样地,求出15m/s风速下误差补偿多项式的系数:
将式(19)所得系数代入误差补偿多项式(12)可得到风速的多变量拟合表达式,经过误差补偿后结果如表7和图6所示。
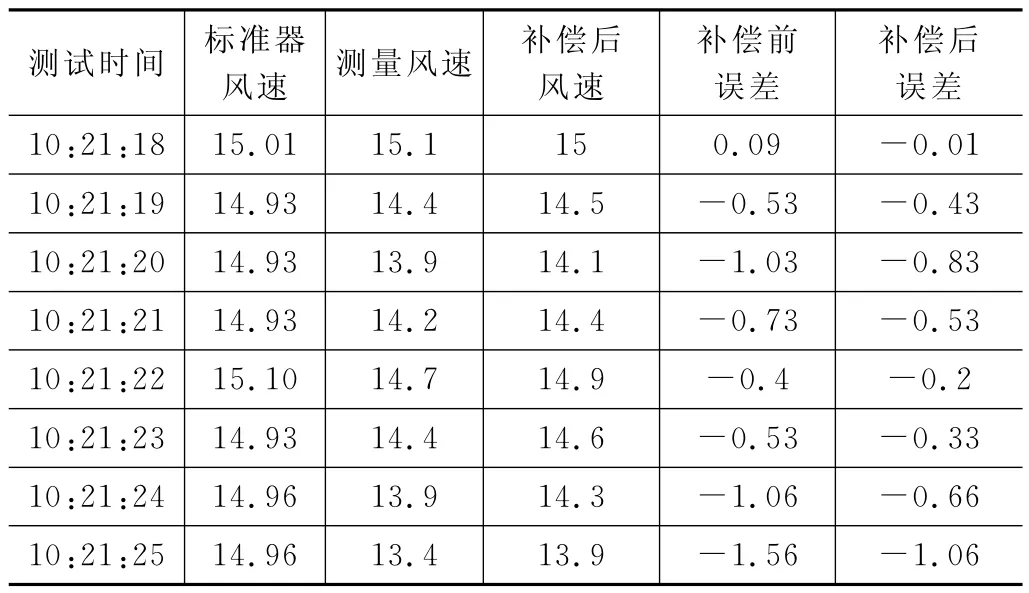
表7 15m/s风速下误差补偿结果 m/s

图6 15m/s风速下误差补偿结果
经过误差补偿后,风速测量误差结果区间为:-1.06~0.01m/s,相较于补偿前误差结果也得到明显改善。综上可知,通过多变量拟合的方法对动态风速测量误差进行拟合能够有效减小测量误差。
3.3.2 风向测量数据误差补偿
同样地,对风向测量误差(设为ΔD)与俯仰角θ和横滚角γ的变化值建立多变量拟合误差表达式:
经过所测得的风向数据求解出表达式系数,利用最小二乘法求出表达式系数代入式(20)得到多变量拟合表达式,从而得出风向测量误差与俯仰角θ和横滚角γ之间的关系,对动态测风风向误差结果进行误差补偿。
经过校正处理后,风向测量数据误差补偿结果如表8和图7~9所示。

表8 动态风向测量数据误差补偿结果 (°)

图7 5m/s风速下风向误差补偿结果

图8 10m/s风速下风向误差补偿结果
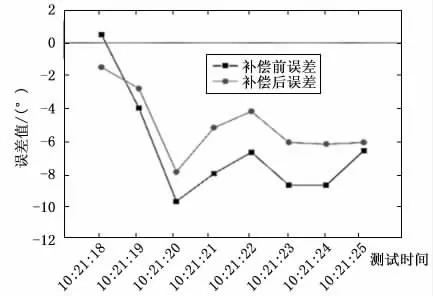
图9 15m/s风速下风向误差补偿结果
3.4 实验结果与分析
经过上述实验结果分析可知,经过误差补偿后,5m/s风速下风速测量误差区间由-0.61m/s~0.13m/s减小到-0.34~0.04m/s;10m/s风速下的风速测量误差区间由-1.17~0.33m/s减小到-0.77~0.13m/s;15m/s风速下的风速测量误差区间由-1.56~0.09m/s减小到-1.06~0.01m/s。相较于补偿前风速测量误差结果均得到明显改善。对于风向测量数据,经过误差补偿后,风向测量误差整体有所减小。总体呈现出测试点误差较大时补偿效果较好,测试点误差较小时补偿效果不太好,甚至有所增大,但是经过补偿后误差效果整体更优。综上可知,通过多变量拟合法对动态风速风向测量误差进行补偿能够有效减小测量误差。
4 真风订正算法设计
漂流浮标的工作场所在海上,在动态海况条件下,装载于漂流浮标上的超声波测风传感器测量出的风速风向数据并不是自然情况下的真实值。经过前面动态环境下测风误差补偿后,还应该考虑由漂流浮标随洋流移动速度、方向的影响。当然,根据需要有时还需考虑由海面湍流等因素造成的浮标体旋转带来的测风误差。
将漂流浮标上搭载的超声波测风传感器所测风速风向值,结合姿态测量模块所测出的漂流浮标姿态信息,经过测风误差补偿后,还应再结合漂流浮标上安装的GPS定位系统所测出的浮标漂流速度和漂流方向进行真风订正计算,最终得到海面真实风速风向值。
综上,可得真风计算公式:
根据平行四边形法则定理,由下列公式便可得出真实风速风向值:
式中,DV为视风风向;SV为视风风速;SS为船风风速;ST为真风风速;DS为船风风向;DT为真风风向。
将前面误差补偿后的风速风向数据与真风订正算法相结合,便可以得到如下海洋漂流浮标测风算法流程:
1)采集漂流浮标上超声波测风传感器所测实时风速Vc和风向Dc的值,以及同轴安装测姿模块所测同时刻的俯仰角θ和横滚角γ的值;
2)得出实时风速风向测量误差与对应时刻传感器俯仰角θ和横滚角γ的多变量误差补偿表达式;
3)应用有限元法和最小二乘法得到误差补偿表达式的系数,从而得到补偿后的风速Sv和风向Dv的值;
4)最后,根据GPS定位系统所测得的“船风”风速Ss和风向Ds值,结合真风订正算法求出真实海况下的风速风向值。
5 结束语
本文模拟海洋动态观测环境,分别对5 m/s、10 m/s和15m/s风速下的风速风向数据进行观测分析,发现传感器俯仰角θ和横滚角γ对风速风向测量影响最大。于是,提出使用多变量拟合的方法对误差进行补偿,通过实验中测得的多组动态倾角下的风速风向测量数据与风洞标准值进行对比,建立了测量误差与俯仰角θ和横滚角γ的误差补偿多项式,从而得到误差值与这两个变量的关系,进而对风速风向数据进行误差补偿。对比补偿前后的数据,风速测量数据经过补偿后误差明显减小,风向测量值经过补偿后,准确度也有了较大提高,可以作为海洋气象漂流浮标测风技术误差补偿方法使用。该误差补偿算法在实验室测试阶段数据较为可靠,但仍可增加其他误差补偿方法与之进行对比,得出更优的补偿方法。最后,结合真风订正算法设计了真实海况下漂流浮标测风算法总的测试流程,为后续真实海况下漂流浮标测风提供技术支撑。

