基于PSO-BP神经网络的小冲孔蠕变寿命预测模型

王 杰 郑杨艳 凌 祥

（南京工业大学a.机械与动力工程学院；b.能源科学与工程学院）

在航空航天、石油化工等行业中，高温服役的金属构件材料性能随着服役时间逐渐劣化，寿命缩短，提前或者突发性破坏极易造成重大经济损失，产生灾难性的后果。对高温服役的金属构件进行蠕变损伤分析、寿命评估是保证构件安全运行的必要手段。为避免对在役构件造成破坏，小冲孔试验技术作为一种微型测试技术，在蠕变寿命预测方面与传统蠕变试验有相似的3个阶段，对服役设备寿命预测已经在石油、化工等领域被逐步应用［1］。

20世纪90年代，PARKER J进行了小冲孔蠕变试验，提出小冲孔蠕变试验技术可以用于对材料高温蠕变特性的建立，表明了小冲孔试验技术在高温领域的可行性［2］。目前，小冲孔蠕变寿命的预测主要通过短期温度或载荷函数进行外推，预测材料蠕变的寿命。DOBEŠ F和MILICˇKA K基于Monkman-Grant模型使用最小蠕变速率和断裂时间建立了小冲孔蠕变寿命预测公式［3］。文献［4～8］的研究者基于Larson-Miller参数法，成功估算了不同材料的蠕变寿命。YANG S S等基于小冲孔能量模型推断不同材料在恒温下的蠕变寿命［9］。ZHENG Y Y等以20%蠕变寿命作为小冲孔蠕变寿命预测的起点，使用修正Theta法成功预测了已服役材料的寿命［10］。JEFFS S P等使用Wilshire方程根据短期蠕变数据预测长期蠕变寿命［11］，而后，HOLMSTROM B等提出一种可直接用于小冲孔蠕变测试的修正Wilshire方程［12］。近年来数据驱动的机器学习在蠕变寿命预测方面发展迅速。VENKATESH V和RACK H J采用反向神经网络并得到了很好的预测精度［13］。LIU Y等将机器学习应用到镍基单晶高温合金的蠕变断裂寿命预测［14］。

笔者建立一种基于粒子群算法（PSO）优化的BP神经网络的小冲孔蠕变寿命预测模型，克服工程中难以获得解析解和无法通过经验解描述高维变量之间非线性交互的局限性，实现对小冲孔蠕变寿命的预测，节约试验成本，并与传统BP神经网络预测模型进行对比分析。

1 PSO-BP神经网络模型

1.1 BP神经网络

20世纪80年代，Rumelhart和McClelland提出了利用误差反向传播训练算法的神经网络，即BP神经网络（Back-Propagation Network），目前已成为应用最广泛的神经网络模型之一［15］。该模型使用梯度下降的搜索方法，利用反向传播优化神经网络的权值和阈值，最终使得输出值和期望输出值的均方根最小，具有很好的容错性泛化能力［16，17］。BP神经网络模型具有3层拓扑结构，包括输入层（Input Layer）、隐含层（Hidden Layer）和输出层（Output Layer）。大量研究表明含有一个隐含层的神经网络可以实现对任何函数的逼近［15］，为避免模型过于复杂而引起计算量过大或预测结果不可靠的问题，构造单隐含层的BP神经网络，其结构如图1所示。

图1 单隐层BP神经网络结构图

如图1所示，输入层和输出层数据集维度分别为n、m，对应为实际问题中自变量和因变量个数，隐含层神经元个数即节点数为p。各层之间的连接权重分别为ωij（i=1，2，…，n；j=1，2，…，p）和νij（i=1，2，…，p；j=1，2，…，m）。

1.2 PSO算法

粒子群优化算法（Particle Swarm Opitimization）是由Eberhart和Kennedy受到鸟类群体觅食过程的启发，通过群体中个体之间的竞争和协同寻找最优值所创立的一种群体自适应搜索算法［18］。

种群由粒子构成，位置和速度是每个粒子所包含的基本信息。设种群规模为n，目标搜索的空间维数为D，则第i个粒子在D维空间中位置表示为Xi=（xi1，xi2，…，xiD），速度表示为Vi=（vi1，vi2，…，viD），其中i=1，2，…，n。粒子会在迭代中修正自身的位置和速度，直至找到全局范围内的最优位置，其中单个粒子最优位置为Pibest，粒子群最优位置为Pgbest。粒子位置和速度的更新依据为：

1.3 PSO优化BP算法

BP神经网络在预测时容易产生收敛速度慢、易陷入局部极值及学习过程中易发生振荡等问题，采用PSO算法优化BP神经网络，根据粒子位置和速度修正BP神经网络中的阈值和权值，以期提高BP神经网络的运行速度和泛化能力。笔者将粒子群优化算法（PSO）与BP神经网络结合，其流程如图2所示。

图2 PSO-BP流程图

2 基于PSO-BP的小冲孔蠕变寿命预测模型

2.1 模型建立

将PSO优化BP神经网络应用于小冲孔蠕变寿命预测中，建立如图3所示的小冲孔蠕变寿命的预测模型，模型共分为5个模块：试验数据采集模块、特征数据提取模块、数据处理模块、基于PSO-BP的小冲孔蠕变寿命预测模块和数据接收模块。

图3 小冲孔蠕变寿命的预测模型结构

首先用试验数据采集模块对小冲孔试验进行实时数据采集，其次用特征数据提取模块提取小冲孔试验中的温度、载荷和对应条件下的破断时间，然后数据处理模块将所提取的特征数据采用MATLAB提供的mapminmax函数进行归一化处理，接着基于PSO-BP的小冲孔蠕变寿命预测模块将归一化处理后的部分数据进行网络训练并将剩余数据用于验证测试，最后由数据接收模块接收寿命预测模块所输出的数据。

2.2 试验数据

针对小冲孔蠕变破断时间的预测问题，选取JEFFS S P和LANCASTER R J对第2代镍基单晶高温合金CMSX-4在不同温度和载荷下所做的小冲孔蠕变试验数据进行分析［19］。CMSX-4拥有较高的高温强度、优异的蠕变与疲劳抗力、良好的抗氧化性、抗热腐蚀性、组织稳定性和使用可靠性，已经成为先进航空发动机高压涡轮叶片和地面燃气轮机叶片的关键材料［20］。

CMSX-4的合金成分及其含量见表1。小冲孔蠕变试验分别在950、1 050、1 150 ℃3种温度、50～400 N载荷范围下进行，共获得17组蠕变试验数据（图4）。

表1 CMSX-4的合金成分及其含量wt%

图4 不同载荷、温度下小冲孔蠕变破断时间

2.3 参数设置

为了保证寿命预测模型的可靠性，随机选取上述试验中14个不同温度、载荷条件下的小冲孔破断时间作为模型训练样本，剩余3个作为模型测试样本，需要注意的是，3个测试样本应尽可能选择不同温度，并进行多次重复试验。

本模型构造单隐含层网络，隐含层的神经元数为通过寻优获得的最小均方误差所对应的最佳节点数。训练迭代的最大次数为1 000，学习速率为0.01，期望误差为0.001。PSO算法的粒子群规模n=10，惯性权重ω=0.8，进化次数为30，学习因子c1=c2=1.99445。

3 结果及对比分析

采用MATLAB编程模拟神经网络的训练过程，得到如图5所示的算法学习性能。

图5 算法学习性能

图5a所示的BP神经网络的算法性能中，前7步3条误差线几乎重合，7步之后逐渐分开，迭代次数为105时得到的训练误差最小，为3.6746×10-5；图5b所示的PSO-BP神经网络的算法性能中，前5步3条误差线几乎重合，5步之后逐渐分开，迭代次数为11时得到的训练误差最小，为1.2779×10-5；两种预测模型对比可知，基于PSO优化的BP神经网络收敛速度块，均方误差小且整体性能好。

为了检验基于PSO-BP神经网络的小冲孔蠕变寿命预测模型的准确性和稳定性，采用多次随机抽取测试样本的方法对模型的预测结果进行误差分析，预测结果见表2，预测结果对比如图6所示。

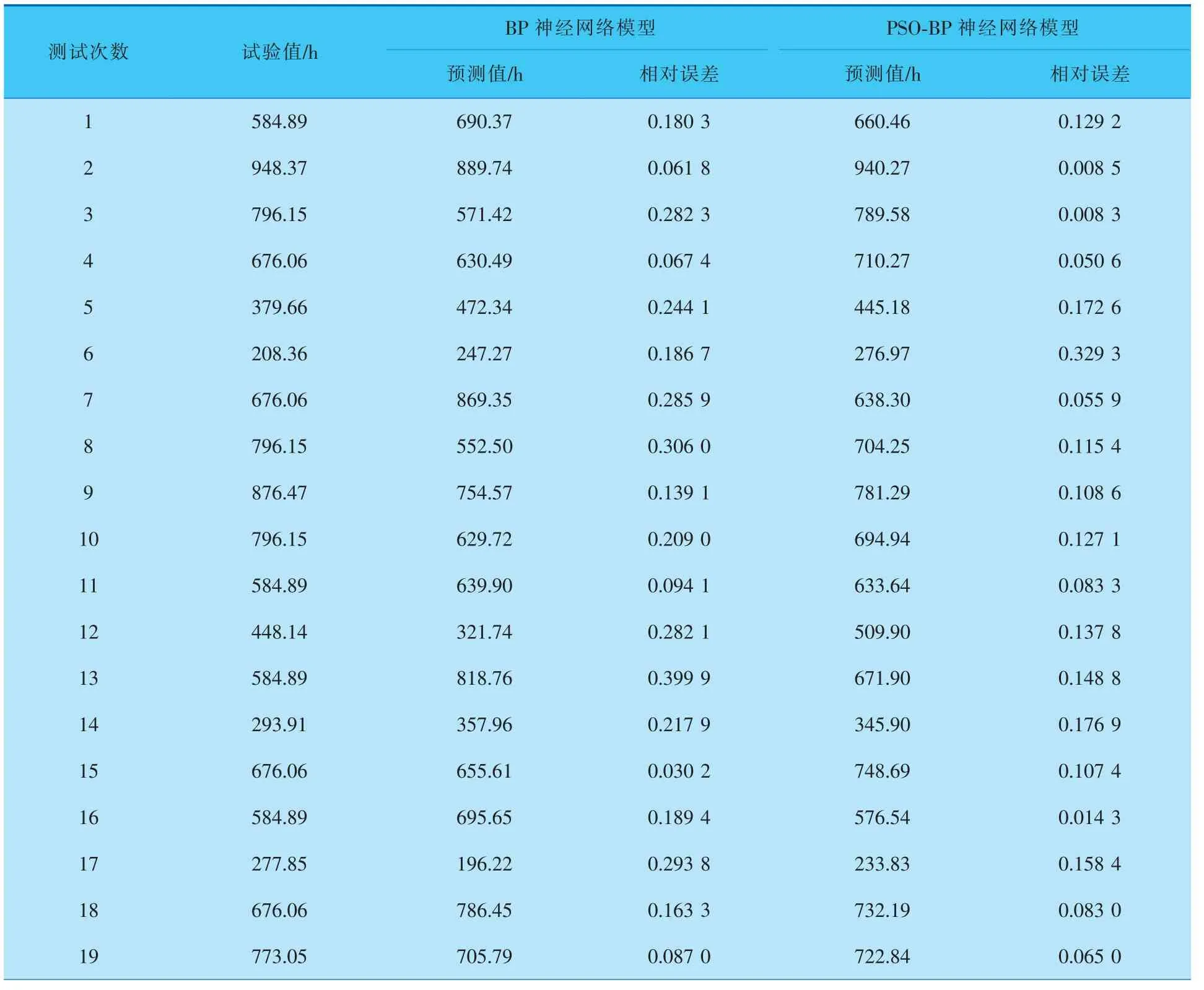
表2 预测结果与误差分析

图6 破断时间预测结果对比

由图6a可知，PSO-BP神经网络预测模型的预测值相较于BP神经网络更接近试验值，预测结果更加准确。结合表2、图6b可知，PSO-BP预测模型最大相对误差为0.329 3，平均相对误差为0.102 2；传统BP神经网络的最大相对误差为0.399 9，平均相对误差为0.182 5。考虑到蠕变试验因为实际试验条件的不确定性，有学者指出蠕变试验的破断时间偏差在20%以内均可接受［21］。在第6次测试中，BP神经网络预测值为247.27 h，相对误差为0.186 7；PSO-BP神经网络预测值为276.97 h，相对误差为0.329 3，与实际值208.36 h误差更为显著，可能是蠕变试验的误差，也可能是模型自身仍存在一些问题。但整体情况而言，基于PSO-BP神经网络的小冲孔蠕变寿命预测模型预测结果符合实际应用情况，且相较于传统BP神经网络泛化能力更胜一筹。

4 结论

4.1 采用粒子群优化算法（PSO）优化了BP神经网络的权值、阈值，根据不同温度和载荷下小冲孔蠕变破断时间，建立基于PSO-BP神经网络的小冲孔蠕变寿命预测模型，解决了BP神经网络收敛速度慢、易陷入局部极值的问题，提高了小冲孔蠕变寿命的预测精度。

4.2 用PSO-BP神经网络小冲孔蠕变寿命预测模型多次随机选取测试样本进行预测，破断时间预测结果与试验值的平均相对误差为0.102 2，BP神经网络预测模型的平均相对误差为0.182 5，基于PSO-BP神经网络的小冲孔蠕变寿命预测模型预测精度较BP神经网络更高，稳定性更好，且预测相对误差除第6次试验，其余均在蠕变试验破断时间偏差范围内，达到很好的预期，符合实际要求。

4.3 笔者建立的基于PSO-BP神经网络的小冲孔蠕变寿命预测模型预测精度整体较好，但其惯性权重、学习因子等参数还需要依据经验进行选取，缺乏相应理论的指导，在第6次测试中误差显著，如何选取预测模型参数提高预测的准确性和稳定性仍需要进一步研究。