矮塔斜拉桥塔梁墩固结粘接部位局部模型构建与应力分析
易成
摘 要:采用塔梁同步施工工艺可以在一定程度上缩短矮塔斜拉桥的施工工期,但也会给塔梁墩固结粘接部位局部应力形成较大影响。研究以我国兰合铁路某段矮塔斜拉桥为例,对该工程开展同步施工阶段矮塔斜拉桥塔梁墩固结粘接部位局部模型进行构建,分析了该工程局部应力分布规律,通过模型模拟分析结果与实际工程测试数据对比,对该模型的准确性进行验证。
关键词:矮塔斜拉桥;塔梁墩;固结粘接部位;分析模型;局部应力
中图分类号:U445.58+8
文献标志码:A文章编号:1001-5922(2023)04-0162-04
Local model construction and stress analysis of consolidation and bonding parts of pier of short tower cable-stayed bridge
YI Cheng
(China Railway First Survey and Design Institute Group Co.,Ltd.,Xian 710043,China)
Abstract:The construction period of short tower cable-stayed bridge can be shortened to a certain extent by using the tower beam synchronous construction technology,but it also has a great influence on the local stress of the consolidation and bonding parts of tower beam pier.Taking a short tower cable-stayed bridge of Lanhe Railway as an example,a local model of the consolidation and bonding position of the tower girder pier of the short tower cable-stayed bridge during the synchronous construction phase of the project was constructed.The local stress distribution law of the project was analyzed and the accuracy of the modified model was verified by comparing the model simulation analysis results with the actual engineering test data.
Key words:low-pylon cable-stayed bridge;tower beam pier;consolidation and bonding site;analysis model;local stress
傳统的矮塔斜拉桥在施工过程中大多会选择先塔后梁的技术,即先对矮塔进行建设后再开展梁等部分的建设。为了优化工期,部分矮塔斜拉桥在施工过程中逐渐摒弃了这种先塔后梁的技术,选择了塔梁同步施工工艺[1]。这种施工工艺能够根据建设项目的工程特点大大缩短施工时间。然而,塔、梁的同步施工会给塔梁墩固结粘接部位局部应力带来较大的影响,如果计算不当有时会给工程带来巨大的风险。因此,本文以我国兰合铁路某段矮塔斜拉桥为例,建立了一种专门针对塔梁同步施工工艺塔梁墩固结粘接部位局部应力的分析模型,通过该模型监控和分析塔梁同步施工过程中各局部应力的变化情况,以掌握矮塔斜拉桥塔梁墩固结粘接部位局部应力分布规律,保证相关工程建设的合理、安全。
1 项目背景
1.1 项目概况
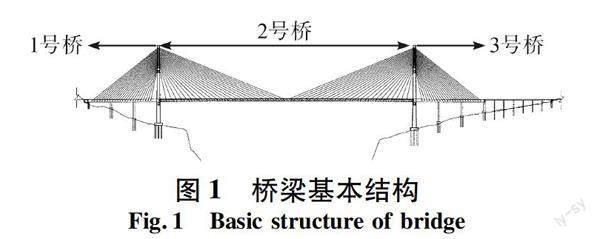
该项目位于兰合铁路某段,整体分为3个不同桥垮,其中1号桥跨全长135 m,2号桥垮240 m,3号桥垮195 m。图1为该桥梁的基布结构示意图。
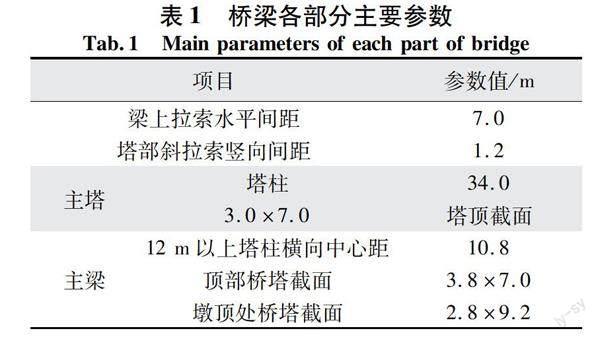
从图1可以看出,该桥梁为典型的矮塔斜拉桥,其拉锁为双索面扇形布置,图中所示部分总共设置44对斜拉索,项目施工主要结构包括路基、桥梁、隧道、互通、涵洞工程等[2];桥墩固结粘接部位采用低水化热水泥,如矿渣硅酸盐水泥粘接加工所成。桥梁各部分主要指标参数值如表1所示。
1.2 设计荷载
该桥梁总质量23 540 t,设计载荷挂篮每套重2 550 kN,共设计斜拉索44对,设计合拢吊架质量350 kN。表2为该桥梁部分矮塔斜拉索设计索力值。
梁伸缩缝过渡区环氧树脂混凝土砂浆初凝时间高于0.5 h;3 d养护龄期的桥梁伸缩缝过渡区环氧树脂混凝土的抗压强度约89.7 MPa,抗折强度约21.8 MPa,粘接强度为2.86 MPa,弹性模量为14.8 GPa,斜拉索设计索力值可以达到桥梁设计载荷的需求。经过紫外老化和湿热老化处理后,矮塔斜拉桥塔梁墩固结粘接部位力学性能需要超过国家水泥混凝土路面设计特重交通等级水凝混凝土强度规定;同时,还需要具有良好的耐老化性能。
1.3 矮塔斜拉桥塔梁同步施工步骤
塔梁同步施工主要指的是矮塔斜拉桥的大桥主体上部分结构和主梁部分则采用悬臂浇筑的方法进行施工[3]。塔梁同步施工中转体部分位于第2跨和第3跨,设计采用钢箱梁T型刚构。图2为该项目的主要施工步骤。
矮塔斜拉桥的同步施工共经历2条不同线路,主体上部分结构经过塔柱支架施工、塔柱施工、若干次斜拉索施工等步骤;主梁部分则采用支架现浇、矮塔斜拉桥施工、若干次挂篮悬浇和吊架现浇合龙等步骤[4]。2条路线经过同时施工实现矮塔斜拉桥的同步施工。
2 矮塔斜拉桥塔梁墩固结粘接部位局部模型构建
2.1 模型构建逻辑
本次构建矮塔斜拉桥梁墩固结部位局部模型主要目的为分析该桥梁在开展同步施工时的局部应力情况。在进行模型构建时以Midas系列软件对桥梁的整体杆模型进行搭建,再以该整体杆模型为基础对梁墩固结部位在不同施工步骤、边界连接等情况下进行网格划分,得到矮塔斜拉桥塔梁墩固结粘接部位局部模型并进行应力分析[5]。
2.2 梁墩固结粘接部位局部模型构建
2.2.1 计算模型范围选取与网格划分
根据文献[6]提出的理论,将该矮塔斜拉桥中心位置为原点,以对称的方式向矮塔斜拉桥2延伸方向各取24 m为一阶段进行x轴划分,以19 m为一阶段进行y轴划分;图3为该矮塔斜拉桥塔梁墩团结部位局部网格划分图。
图3矮塔斜拉桥塔梁墩固结部位局部网格划分图以原点为对称点,将对称点处界面设为第0号块,以原点所在位置的垂直截面为对称面将模型分为2部分。其中主塔、主梁及桥墩部分为固结部位核心构件,该构件向下0~8.5 m将矮塔斜拉桥塔梁墩固结部位局部网格按照每0.3 m一阶段进行划分;该构件向下8.5~29 m按照每0.5 m一阶段进行划分;该构件向下29 m以下按照每1.0 m一阶段进行划分[7]。
2.2.2 预应力钢束模拟
该项目的应力分析只考虑矮塔斜拉桥桥梁主梁的x轴与y轴预应力钢筋作用。在对塔梁墩固结部位进行预应力钢束模拟时,利用Midas系列软件内的强化功能赋予图4所示,矮塔斜拉桥塔梁墩固结部位局部网格划分图不同网格各自的特性,将预应力值设定在预应力钢筋的始末两端,通过软件的自主运算得到钢束信息[8]。通过软件分析可知该项目预应力钢筋网格划分尺寸为0.1 m。
2.2.3 主要结构件材料特性
根据以往相同类型工程建设实例采用C55、C50、C40混凝土分别作为矮塔斜拉桥塔梁墩固结粘接部位的主梁、桥塔与桥墩的建筑材料。表3所示为构件各材料的主要特性如弹性模量、泊松比等的统计结果。
2.3 梁墩固结粘接部位局部应力分析
以0号块对称面中心点为原点设定距离该原点处沿x轴方向0、3.5、4.6、6 m位置处分别为梁墩固结部位中心处、横隔板纵向中心处、主梁悬臂根部、梁墩固结部位0号块端部节点,以0号块对称面中心点为原点设定距离该原点处沿y轴方向0、2.7、5.1、6 m位置处分别为梁墩固结部位中心处、箱式顶板中心、边腹板内表面、边腹板外表面节点,开展纵向正应力分析、横向正应力分析等。
2.3.1 纵向正应力分析
经软件分析后得到表4所示的梁墩固结粘接部位第0号块顶板上缘、底板下缘沿x轴位置及顶板上缘沿z轴位置纵向正应力在最大悬臂状态下的波动情况结果。
从顶板上缘沿x轴方向纵向正应力来看,主梁顶板上缘应力随距中点距离缩小呈现出先减小后升高并略显对称的变化状态,最大应力为据中心点距离12 m处,此时应力可达-16.8 MPa;底板下缘沿x轴方向纵向正应力的变化状态与顶板上缘极为类似,通常随距中点距离缩小呈现出先减小后升高并略显对称的变化状态,最大应力为据中心点距离12 m处,此时应力可达3.6 MPa,但是底板下缘在距中心点-9、-6、6、9、12 m时的差距并不大。
从顶板上缘沿z轴方向纵向正应力来看,主梁顶板上缘应力随距中心点距离缩小呈逐渐增大状态,并于中心点处达到最大值-13.4 MPa;在距离该原点相同距离的-9、9 m等位置纵向正应力的绝对值极为接近,整体分布具有较强的对称性。
2.3.2 横向正应力分析
经软件分析以后得到表5所示梁墩固结粘接部位第0号块顶板上缘沿x轴位置及顶板上缘沿z轴位置横向正应力在最大悬臂状态下的波动情况。
从顶板上缘沿x轴方向横向正应力来看,主梁顶板上缘应力随距中点距离缩小呈现出先增大后减小并略显对称的变化状态,最大应力为据中心点距离-6、6 m处,此时应力可达-3.1、3.33.1 MPa。从顶板上缘沿z轴方向横向正应力来看,主梁顶板上缘应力随距中心点距离缩小呈逐渐增大状态,并于中心点处达到最大值3.9 MPa,整体分布同样具有较强的对称性。
3 模型推测与实测数据对比分析
3.1 顶板应力增量对比
表6所示为模型经过计算后得到的顶板应力增量值与实际施工过程中相同位置的实测数据对比情况结果。
从推测值与实测值对比情况来看,模型推测值最大误差处出现在边跨最大悬臂位置,此时的推测误差约为0.8 MPa;其次为全桥合龙处,误差约为0.7 MPa。其余部分的误差基本集中在0.1或0.2 MPa左右。可见在顶板应力增量分析方面该模型的误差基本在可接受范围内。
3.2 底板应力增量对比
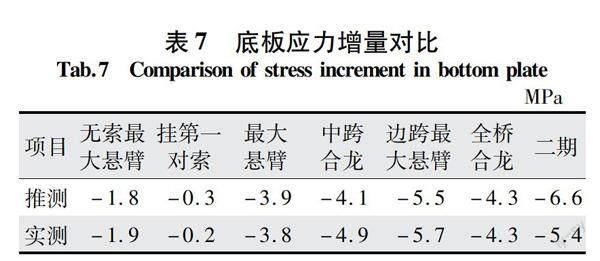
表7所示为模型经过计算后得到的底板应力增量值与实际施工过程中相同位置的实测数据对比情况结果。
从推测值与实测值对比情况来看,模型推测值最大误差处出现在二期环节,此时的推测误差约为1.2 MPa;其次为中跨合龙处,误差约为0.8 MPa;其余部分的误差基本集中在0.1或0.2 MPa左右。可见在底板应力增量分析方面该模型的误差基本在可接受范围内。
綜合来看,该模型基本可以满足矮塔斜拉桥塔梁墩团结部位局部应力分析,其误差主要集中在边跨最大悬臂、全桥合龙、二期及中跨合龙等施工工艺环节。
4 结语
研究以国内某项目为例,对矮塔斜拉桥塔梁墩固结部位局部应力分析模型进行构建,以工程施工中的实测值与模型推测值进行对比。结果表明,该模型除在边跨最大悬臂、全桥合龙、二期及中跨合龙等施工工艺环节的推测值存在一定误差外,其他施工环节的误差很小,基本增量误差均为0.1、0.2 MPa,该模型可以应用在实际的工程施工环节。
【参考文献】
[1] 亢鑫,黄辉,涂满明,等.坦桑尼亚坦桑蓝跨海大桥主桥合龙顺序研究[J].世界桥梁,2023,51(1):9-14.
[2] 桂水荣,雷鸣宇,陈水生,等.矮塔斜拉桥动静力特性对结构参数敏感性影响分析[J].沈阳建筑大学学报(自然科学版),2023,39(1):79-87.
[3] 孙峰.宽幅矮塔斜拉桥分隔带劲芯骨架主塔施工技术分析[J].安徽建筑,2022,29(6):67-74.
[4] 胡豪,施洲.高速铁路矮塔斜拉桥运营阶段收缩徐变效应分析[J].铁道勘察,2022,48(6):128-133.
[5] 张景利.黔张常铁路桥梁总体设计[J].铁道工程学报,2022,39(10):42-46.
[6] 杨德厚,邓同生,李顺波.矮塔斜拉桥塔梁同步施工阶段塔梁墩固结部位局部应力分析[J].交通科技,2021(2):28-33.
[7] 罗书舟,张谢东,赵家胜,等.大跨矮塔斜拉桥模态频率温度影响修正研究[J].武汉理工大学学报(交通科学与工程版),2022,46(5):932-937.
[8] 常心煜,郑祎雷.双塔单索面预应力混凝土矮塔斜拉桥合龙施工技术研究[J].交通世界,2022(25):106-108.

