运用动静结合策略解初中数学平面几何动点问题

摘 要：平面几何是初中数学中的重点内容之一.其中，动点问题常常在中考数学中作为压轴题出现，这类试题能有效考查学生分析和解决问题的能力，较好地渗透了分类讨论、数形结合、化归等数学思想.动点问题较为复杂，导致很多学生遇到相关题目时无法及时找到解题思路.为了帮助学生提高解题能力，本文对中考中平面几何动点问题常考的两大类题型，以2021年两道中考题为例加以分析，并向学生讲解相关的解题策略.

关键词：平面几何；动点；初中数学

中图分类号：G632 文献标识码：A 文章编号：1008-0333（2023）08-0029-03

1 “化动为静”——动边转移求解范围问题

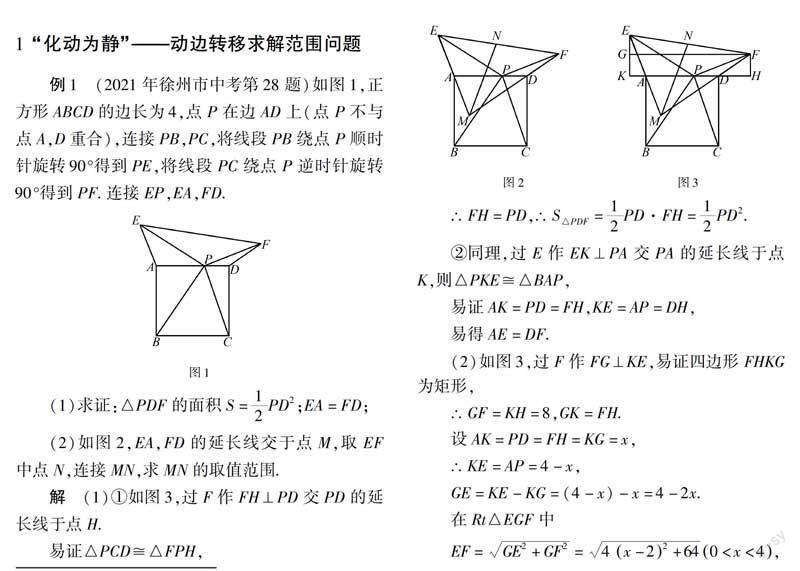
例1 （2021年徐州市中考第28题）如图1，正方形ABCD的边长为4，点P在边AD上（点P不与点A，D重合），连接PB，PC，将线段PB绕点P顺时针旋转90°得到PE，将线段PC绕点P逆时针旋转90°得到PF.连接EP，EA，FD.

3 反思总结，提高学生解题能力

对于动点问题，学生首先要能够明辨题目中的变量和不变量.只有分清楚变量和不变量才能够化动为静，将所求的变量转化到恒定的不变量上.具体问题中通常是将运动的点或边，转移到不变的边上，这样问题也就迎刃而解了.其次，动点在运动过程中的特殊点，也是解题的突破口之一，要抓住关键点，将一般情况特殊化，观察运动过程，进而能够发现动点的运动规律.对于与函数有关的动点问题，要尝试建立动点运动过程中的函数关系，利用函数性质进行求解.

只要掌握了动点问题的解题策略，不论动点怎么动，我们都能以不变应万变，顺利求解此类试题.动点问题常常较为综合，求解过程也要运用多种数学知识，所以能有效地考查学生的数学知识和数学能力，有效区分不同考生的数学学习水平，为中学阶段的选拔提供一定依據.

教师在教学中要注意培养学生的几何素养，有意训练学生的动态思维，将动点问题中的“动”与条件中的“静”结合起来，学会运用数形结合等数学思想方法，再结合专项训练，一定可以提高学生对动点问题的求解能力.

参考文献：

［1］王中文.初中数学动点问题的解题策略[J].读与写（教育教学刊），2012，9（03）：115.

[2] 陈韧.初中数学动点问题的解题策略分析[J].课程教育研究，2018（06）：143-144.

［责任编辑：李 璟］

收稿日期：2022-12-15

作者简介：苏雅（1998.7-），女，研究生，从事初中数学教学研究.