考虑社会网络信任关系的多属性群决策方法
陈宏晨,伊长生
安徽工业大学 管理科学与工程学院,安徽 马鞍山 243032
1 引 言
多属性群决策(MAGDM)是指一群决策者针对具有共同属性的多个备选方案体提供各自的决策矩阵,通过评价选择出群体均满意的备选方案[1]。目前,MAGDM广泛用于管理科学、经济学等多个研究领域,成为解决实际问题的有效工具。
国内外对MAGDM问题已有大量研究,Lin等[2]认为在多属性群决策问题使用TOPSIS法对方案进行排序时会导致属性权重过度加权,提出一种采用Minkowski距离公式解决该问题的方法。姚远[3]针对属性值为不确定语言信息的群决策问题,提出将其转化成正态云模型,并在此基础上利用正态云模型的模糊性与随机性确定属性权重。梁昌勇等[4]提出一种基于TOPSIS的MAGDM方法用于解决方案属性的评价信息为不同粒度语言信息与直觉模糊数两种形式时,如何将不同粒度语言信息转化为直觉模糊数,使决策问题中的评价信息形式趋于一致。
尽管文献[1-4]中的群决策研究对属性问题加以考虑,但均默认属性是完全独立的。然而随着决策环境的复杂程度加大,属性之间也可能存在一定的关联性。针对这类问题,文献[5-6]的相关研究表明属性之间的关联性问题可用Choquet积分算子来计算。
此外,与传统的群决策问题[7-9]中默认决策者之间相互独立不同,互联网与社交媒介的发展使得人与人之间因信任关系、知识情感等方面产生了更多的社会联系,从而形成社会网络。诸多学者从不同的角度针对社会网络与群决策的问题进行了大量研究[10-12]。李胜利等[13]认为决策者的社会关系可以提高决策者的决策能力,于是将由社会关系、知识能力与身份地位融合而成的信任关系用于共识模型中调整与修正共识度最低的决策者的意见,从而提高共识效果。Zhang等[14]提出了一种采用社会网络解决群决策过程中决策者之间出现的不合作行为,即通过计算决策者之间完整的信任关系获取权重大小并用于共识。Wu等[15]则针对社会网络环境下信任关系的传播与聚合如何影响群决策的问题,提出了一种新的算子(UTWA算子)计算完整的信任关系从而获取权重信息。由此可见,信任关系的研究逐步趋于完善。然而,信任与风险是并存的[16],研究发现,决策主体在知识背景等方面的差异性会影响其信任判断,从而导致决策失误[17]。
根据上述分析,针对属性之间具有关联性以及决策者之间可能存在信任风险的决策情况,提出了一种考虑社会网络信任关系的多属性群决策方法。首先,根据社会网络关系对决策者进行聚类并获取相关权重;其次通过信任关系得出信任风险、评价风险的大小,并进行相应的意见调整;然后采用Choquet积分算子解决属性关联性的问题,并在得出方案的综合评价值后对其进行排序获取最优方案;最后将其应用于一个算例中验证其具有可行性。
2 基本知识
2.1 社会网络分析
社会网络分析是一种研究社会成员关系并通过揭示成员内在联系来解释社会现象的有效工具[10-12]。其基本表示方法有图示,代数和邻接矩阵3种。例如,邻接矩阵A表示如下:
其中,1表示决策者ei与ej存在社会联系,0表示两者不存在社会联系。
定义1[12]度中心性表示社会网络中决策者ei直接连接其他决策者的数量。度中心性越大,其直接影响力越高。
定义2[12]特征向量中心性表示决策者ei与社会网络中其他决策者的通信能力,反映其间接影响力。
CE(ei)∝∑AijCE,i≠j,j=1,2,…,n
2.2 信任关系
定义3[15]设(t,d)为集合[0,1]2中的元素,称(t,d)为信任得分,t为信任值,d为非信任值,此时信任度TS定义为
(1)
定义4[15]信任关系矩阵为TD=[(tij,dij)]m×m即
2.3 直觉模糊数
定义5[9]设A={(x,μA(x),vA(x))|x∈X}为直觉模糊集。其中μA(x),vA(x)与πA(x)=1-μA(x)-vA(x)分别表示为隶属度、非隶属和犹豫度,并满足条件:
∀x∈X,μA(x)≥0,vA(x)≥0,0≤μA(x)+vA(x)≤1

定义7[9]α=(μα,vα),β=(μβ,vβ)为两个直觉模糊数,令S(α)=μα-vα为得分函数,H(α)=μα+vα为精确函数,则α与β的比较方法如下:
(1) 当S(α)>S(β)时,则α≻β;
(2) 当S(α)>S(β)时,若H(α)=H(β),则α=β;若H(α)>H(β)则α≻β。
定义8[9]设A=(μA(xi),vA(xi))和B=(μB(xi),vB(xi)),i=1,2,…,n为两个直觉模糊集,则A与B之间的Hamming距离为
|πA(xi)-πB(xi)|)
其中,Hamming距离越大,A与B之间的差异性越大。
2.4 Choquet积分算子
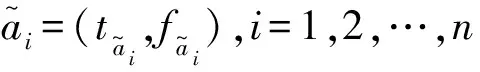
(2)
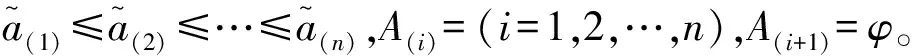
3 基于信任关系的多属性群决策模型
3.1 问题描述

3.2 权重计算与评价值的集结
3.2.1权重计算
利用Gephi将决策者划分为若干个子社区,记为{Tk|k=1,2,…,l},其权重向量记为λ=(λ1,λ2,…,λl)T,且子社区内的决策者数量为nk,1≤nk≤m。根据度中心性与特征向量中心性得到混合中心性C(ei):
(3)
此时决策者ei的权重wi为
(4)
子社区的权重是由子社区与整个群体的混合中心之间的距离确定的,即
(5)
经归一化处理后得到子社区权重λk为
(6)
3.2.2评价矩阵的集结
子社区评价矩阵Rk是由子社区内决策者的评价矩阵集结而成:
(7)
其中,wi∈[0,1],∑wi=1,i=1,2,…,nk。
综合评价矩阵R由子社区评价矩阵Rk集结而成:
(8)
其中,λk∈[0,1],∑λk=1,k=1,2,…,l。
3.3 风险计算
3.3.1信任风险系数
依据TD确定ei的信任度TSi:
(9)
子社区信任度TSTk为
(10)
在信任度较小的子社区内,决策者会因信任程度较低而存在非理智决策的风险。令该子社区的信任风险系数为φ1,则
(11)
3.3.2评价风险系数
在直觉模糊数(μ,v)中μ∈[μ,μ+π],v∈[v,v+π],π表示犹豫度。如图1所示。

图1 (μ,v)的几何示意Fig.1 Geometrical interpretation of (μ,v)

(12)
3.3.3综合风险系数
综合风险系数φ是由φ1与φ2组成,即
(13)
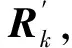
(14)
3.4 方法步骤
步骤1 获取决策者的评价矩阵与TD等。
步骤2 通过Gephi获得子社区。利用等式(3)—式(6)分别确定决策者和子社区的权重,利用等式(7)—式(8)计算子社区评价矩阵与综合评价矩阵。利用等式(9)—式(10)分别确定决策者与子社区的信任度。
步骤3 利用等式(11)—式(13)得出最小信任度的子社区及其风险系数。
步骤4 通过等式(14)得到新的社区评价矩阵以及综合评价矩阵。
步骤5 利用Choquet积分算子确定备选方案的综合评价值,通过得分函数对方案进行排序后筛选最优方案。
4 算例分析
4.1 算例背景
某相关部门针对城市黑臭水治理问题组织了16名决策者进行多属性群决策。通过对时间(C1)、成本(C2)、技术(C3)与环保(C4)这4项属性进行讨论后得出3种备选方案X={X1,X2,X3},分别为:X1表示控源截污以防止外来污染物进一步污染;X2表示清淤疏浚避免出现污染物淤积;X3表示水体置换以增加城市内水体流动性。
4.2 决策过程
步骤1利用Gephi将获取到的社会网络关系可视化后见图2。决策者的评价值见表1。
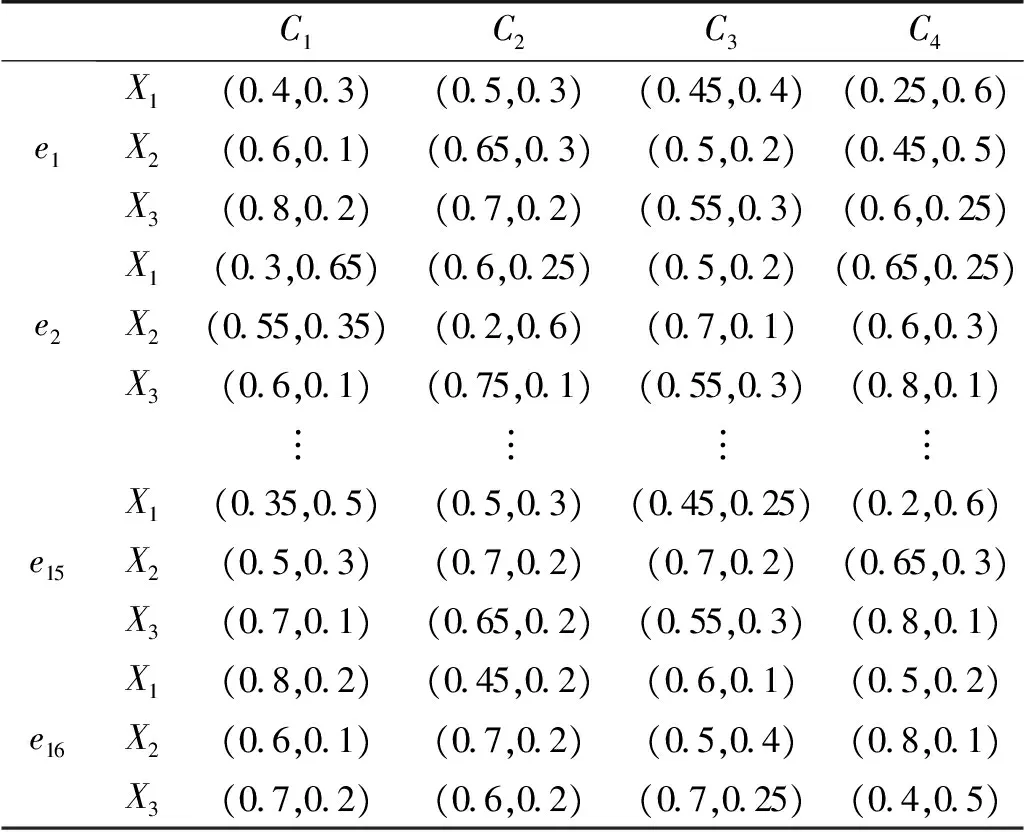
表1 决策者的评价值Table 1 The evaluation values of decision makers
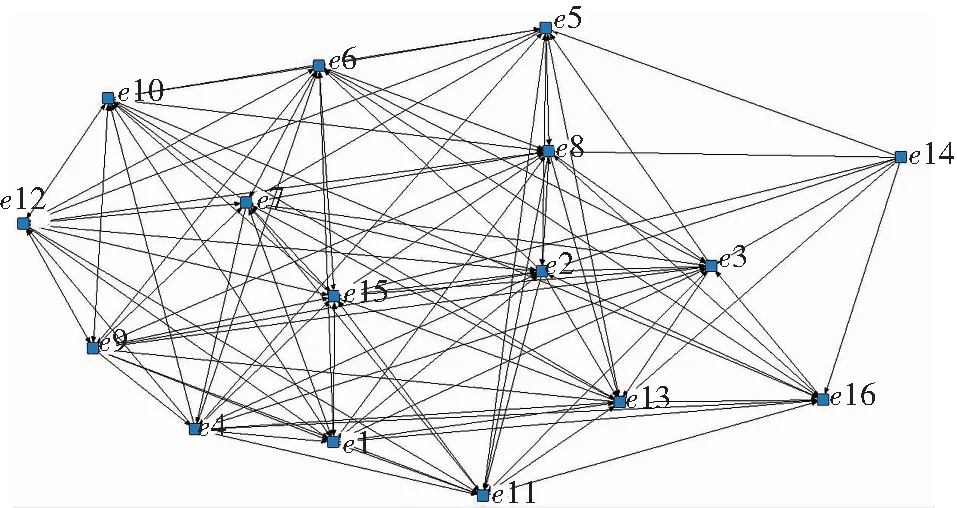
图2 社会网络Fig. 2 The social network
信任关系矩阵为
步骤2 利用Gephi划分出4个子社区,见图3。

图3 社会网络分区Fig. 3 The social network partition
通过等式(3)—式(6)计算出决策者与子社区的权重,结果见表2。根据等式(7)—式(8)得到子社区评价矩阵与综合评价矩阵,分别见表3和表4。利用等式(9)—式(10)计算出决策者与子社区的信任度,结果见表5。

表2 决策者与子社区的权重Table 2 The weights of decision makers and sub-groups
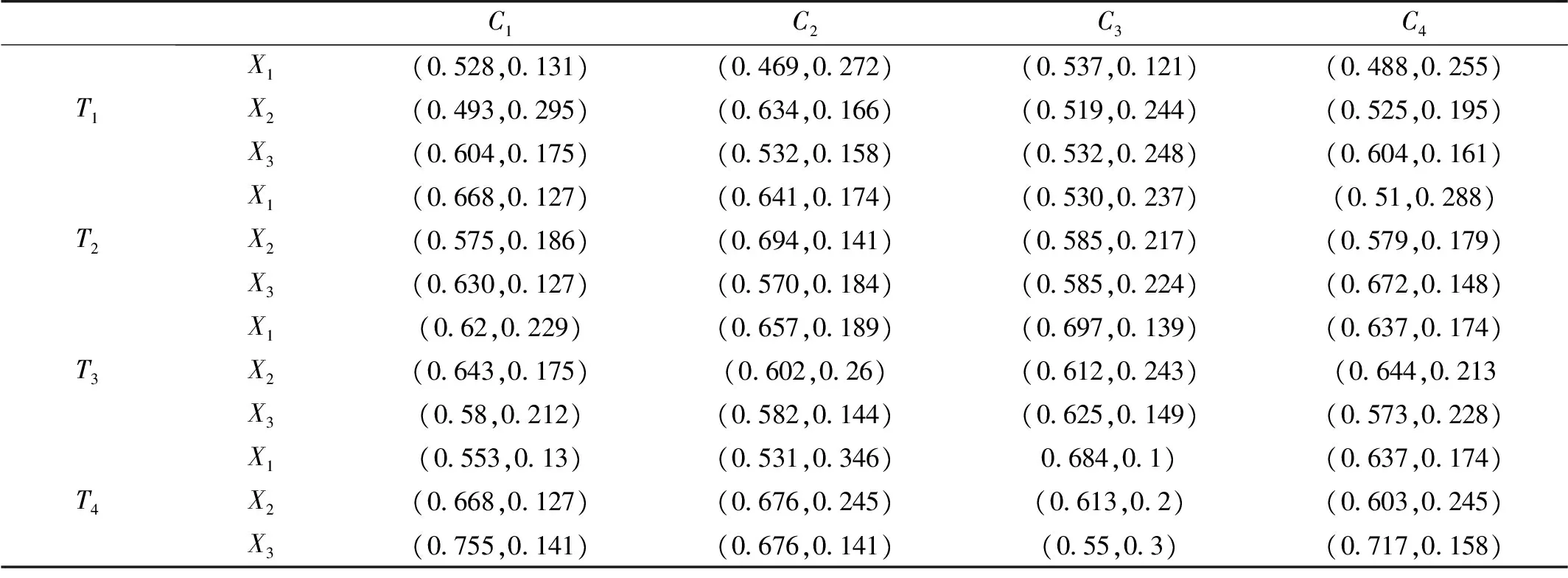
表3 子社区评价矩阵Table 3 The evaluation matrix of sub-groups

表4 综合评价矩阵Table 4 The comprehensive evaluation matrix

表5 决策者与子社区的信任度Table 5 The trust degree of decision makers and sub-groups
步骤3 根据表5看出T1的信任度为0.495,相比其他3个子社区最低。因此根据等式(11)—式(13)得出φ1为0.505,φ2为0.185,φ为0.345。
步骤4 根据等式(14)得到T1新的社区评价矩阵与综合评价矩阵,结果见表6和表7。

表6 T1区新的评价矩阵Table 6 The new evaluation matrix of T1

表7 新的综合评价矩阵Table 7 The new comprehensive evaluation matrix
步骤5 利用Choquet积分算子确定备选方案的综合评价值。
ε(C1)=0.45,ε(C2)=0.25,ε(C3)=0.42,ε(C4)=0.3,ε(C1,C2)=0.75,ε(C1,C3)=0.68,ε(C1,C4)=0.55,ε(C2,C3)=0.5,ε(C2,C4)=0.38,ε(C3,C4)=0.39,ε(C1,C2,C3)=0.87,ε(C1,C2,C4)=0.75,ε(C1,C3,C4)=0.83,ε(C2,C3,C4)=0.64。
此时,方案X1的属性顺序为
a1(1)=(0.589,0.219),a1(2)=(0.606,0.215),a1(3)=(0.62,0.173),a1(4)=(0.63,0.147)。
利用IFWA算子得到X1=(0.617,0.174)。同样地,X2=(0.608,0.198),X3=(0.62,0.171)。此时,S(X1)=0.443,S(X2)=0.41,S(X3)=0.449,则X3≻X1≻X2。即方案X3为黑臭水治理的最优方案。
4.3 分析讨论
在T1区,利用Hamming距离得出考虑风险前后的平均差异分别为0.293与0.222,其精确程度提高了0.071。为了解考虑T1区风险因素的影响,对φ进行适当的敏感性分析,结果如表8所示。其中,d(φ)表示意见修正后的Hamming距离,Δd(φ)表示意见修正前后的差异值。
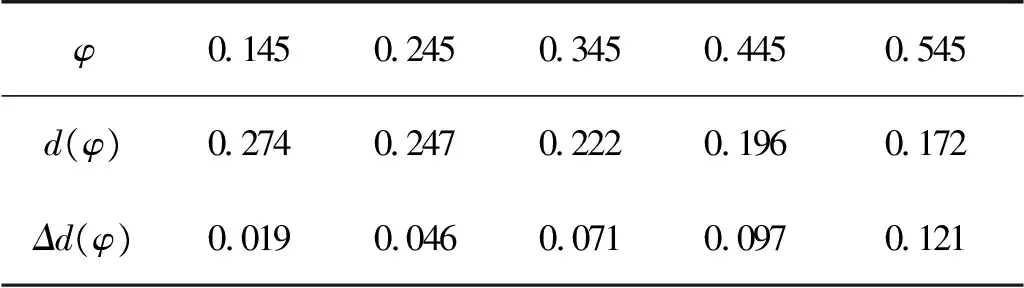
表8 风险变化结果Table 8 The results of risk changes
(1) 将综合风险系数进行调节后得出:
φ=0.145时方案排序为X3≻X1≻X2;φ=0.245时方案排序为X3≻X1≻X2;
φ=0.345时方案排序为X3≻X1≻X2;φ=0.445时方案排序为X3≻X1≻X2;
φ=0.545时方案排序为X3≻X1≻X2。
由此可见,风险大小虽有不同,但X3始终为最优方案。
(2) 随着φ的增大,d(φ)逐渐减小,Δd(φ)也逐渐增大。这说明在综合风险较大的情况下,模型对风险修正的效果也较好。
因此,从算例中可得出考虑风险能够提高决策结果的精确程度。
5 总 结
针对社会网络环境下决策者存在信任关系导致的信任风险,以及方案属性间存在关联性的问题,提出了一种考虑社会网络信任关系的多属性决策方法。一方面,通过社会网络关系将决策群体划分成多个子社区从而降低计算的复杂性。另一方面,通过决策者的信任关系衡量决策风险以提高了决策的精确度,同时又考虑了多个属性之间的关联性,进一步提高决策方案的准确性。并且算例部分也说明了所提方法的可行性。未来将会进一步在关于社会网络环境下信任关系对决策影响的问题上考虑两方面的内容:在所提方法的基础上,考虑信任关系进行传递与集合时如何有效进行多属性群决策;社会网络环境下因信任关系产生的意见领袖如何影响其余决策者进行群决策。

