精巧设计游戏 培育数学眼光

摘 要 游戏是儿童的存在方式，也是儿童学习的需要，小学数学教学需要游戏。小学数学游戏具有趣味性、规则性、体验性、探究性和开放性等特点，利用真实的、生动的、开放的游戏，让学生激情融入学习，引发学生深度思考问题，有着十分重要的意义和价值。通过设计数学游戏，引发生疑、构建概念、发现捷径、打通联系、激活想象等活动的展开，让学生具有数学的眼光，素养得到全面提升，这应当是数学教学的一条有效路径。

关键词 精巧设计 数学游戏 数学眼光

作者简介：洪建林（1970—），男，江苏如皋人，江苏如皋经济技术开发区实验小学正高级教师、特级教师，大学本科，研究方向：小学数学教育。

游戏是儿童的存在方式，也是儿童学习的需要。在整个小学阶段，数学教学都需要游戏，这符合儿童的认知特点和年龄特征。小学数学游戏具有趣味性、规则性、体验性、探究性和开放性等特点，利用真实的、生动的、开放的游戏，让学生激情融入学习，引发学生深度思考问题，这有着十分重要的意义和价值。新课标指出，在义务教育阶段，数学眼光是核心素养的主要内容之一，主要表现为：抽象能力（数感、量感、符号意识）、几何直观、空间观念和创新意识[1]。通过设计数学游戏，引发生疑、构建概念、发现捷径、打通联系、激活想象，让学生具有数学的眼光，素养得到全面提升，这是数学教学的一条有效路径。

一、于游戏中引发生疑，着力于“问题驱动”

问题是数学的心脏。数学眼光的一个重要含义是在各种现实和数学的问题情境中，“看”出其中的数学规律，发现和提出有意义的数学问题[2]。而游戏是学生喜欢的学习方式，能够吸引学生主动参与，在游戏活动中生发疑问，通过问题驱动，能够更好地培育学生的数学眼光。

比如，教学3的倍数的特征时，一位教师设计了这样的游戏导入情境：

游戏抢答：

（一）准确判断下面哪些数是2的倍数？哪些数是5的倍数？哪些数是3的倍数？看谁又对又快！

25、33、126、69、120、5460

（二）准确判断下面哪些数是3的倍数？看谁又对又快！

83、236、460、2009、1393、1767、8547、8457

由于学生已经学习了2的倍数和5的倍数的特征，他们的抢答游戏进行得很顺利，抢答时只要看个位上的数，便迅速进行判断。而对于3的倍数，在抢答题（一）中，学生依然顺利：看个位上的数，个位上是0、3、6、9的数，恰好是3的倍数，结果都是正确的（一些学生自认为发现了3的倍数的特征，甚至有些沾沾自喜）；但是，再看抢答题（二），学生一个个愣住了，他们一个接着一个出错，抢答不断失败，个位上的数是0、3、6、9的数，竟然没有一个数是3的倍数。学生顿生疑惑：怎么方法不能适用了？前面5个数都不是3的倍数！也有同学说：看十位上的数，但学生依然是连续出错。而8547、8457这两个数，没有哪个数位上的数是3的倍数，这两个数却都是3的倍数。

两次比赛引发了学生的认知冲突，教师充分利用游戏资源，引领学生提出不同层次的问题：（1）3的倍数的特征与2或5的倍数的特征一样吗？（2）一个数只看个位上的数，一定能判断它是或者不是3的倍数吗？（3）如果只看个位上的数还不能判断，那应该看哪一位上的數呢？（4）3的倍数一定与一个数的某个具体数位上是几有关系吗？（5）一个数的各位上的数都不是3的倍数，这个数可能是3的倍数吗？（6）3的倍数与各个数位上数的排列顺序有关吗……这些问题驱动学生不断进行数学思考。

教师巧妙设计游戏情境，设计学习“陷阱”，从游戏抢答（一）“很有趣，方法太简单了”，到游戏抢答（二）“方法不灵验了”……学生始终在强烈的认知冲突中发现问题、提出问题，这样的问题弥足珍贵。要把发现和提出数学问题作为学生学习数学、理解数学的一种基本方式，帮助学生形成和发展“数学眼光”。因此，教师在教学中不能只专注于解决问题，也要通过问题意识的培养更有效地促进数学眼光的形成。

二、于游戏中构建概念，致力于“经验积累”

每一个数学概念、关系和结构的发生发展都涉及三种过程：历史过程、逻辑过程、心理过程。加强概念教学是使学生形成和发展“数学眼光”的一条基本途径。通过设计有趣、有意味的游戏，我们可以让学生经历探寻数学历史的路径，看到数学知识的来龙去脉，体验从具体到抽象的生动过程。

例如，教学认识平行时，一位教师设计了这样的游戏：

游戏一：玩中分

1.玩一玩：如果将两根小棒自由落到地面，看看可能会形成哪些图形？

可以画下来哟！

2.分一分：将你画出来的图形试着分类。

3.议一议：你是怎样分类的？

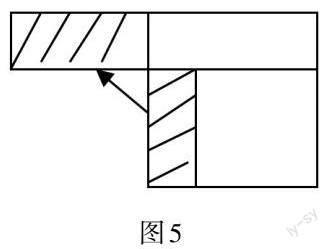
游戏二：玩中辨（见图1）

1.看谁找得多：正方体的每一个面都是正方形，请你找出与线段AB平行的线段。

2.看谁辨得准：线段AB与线段CC1不相交，而是平行，这样的判断正确吗？

游戏一的活动中，各小组的学生画得丰富多彩，如图2：

在分类的过程中，不少学生将以上图形分成两大类：一类是相交的：①②④；一类是不相交的：③⑤。为了验证图形③、⑤的两条直线是否相交，教师再次组织学生进行辩论、操作，让学生将直线分别向两端延伸，奇迹出现了，图形⑤的两条直线竟然相交了，而图形③的两条直线分别向两端无限延伸，总是不相交的。通过操作、比较，学生重新进行分组，认为图形③作为一类，两条直线具有永不相交的特点，揭示了平行线的本质之一。

游戏二是让学生观察一个正方体，与线段AB平行的线段学生比较容易找到，加深了学生对于平行线概念的理解；但是，对于“线段AB与线段CC1不相交，而是平行”这一观点，有学生赞同，也有学生不赞同。教师借此让学生感受何谓“在同一平面内”，并通过电脑“动画”游戏展示两条线段不在同一平面内，虽然具有“不相交”的特点，但不是相互平行的，进一步深化学生对概念的认识。

基于游戏，展开数学概念的教学，这有利于学生积累丰厚的经验，由操作游戏，到表象建立，再到概念建立，学生不断积累操作经验、思维经验，在观察、比较、分析、辩论、抽象、概括、应用等过程中深度体验形成的历史、逻辑和心理过程，从而使自己的数学眼光更精准、更深邃。

三、于游戏中发现捷径，用力于“几何直观”

教师在教学中把几何直观运用得越充分，直观的效果越明显，学生的直观表现意识就会越强烈。数学眼光的培育总是与几何直观紧密联系，教学时需要教师十分关注并用力于几何直观。

在教学了正方形的周长和面积后，一位教师设计了一道趣味闯关题：

小明用一根长22米的绳子围成一个正方形，小华用一根长18米的绳子围成一个正方形，小华围成的正方形面积比小明围成的小多少平方米？在30秒内快速抢答，比一比，看谁口算快！

一些学生进行计算：22 ÷ 4 = 5.5（米），5.5 × 5.5 = 30.25（平方米），18 ÷ 4 = 4.5（米），4.5 × 4.5 = 20.25（平方米），30.25 - 20.25 = 10（平方米）。由于是抢答游戏，学生一下子怔住了，这样的小数乘法口算真是不容易呀！学生悱愤之际，教师利用电脑画出了这样的示意图，继续借助电脑引领学生进行拼图游戏。你能尝试拼图，发现其中的规律吗？

拼图，是小学生从幼儿园起就喜欢玩的游戏。学生在小组内尝试操作，于是，有学生通过剪一剪、拼一拼，拼出了下面的图形：

这一巧妙操作，具有浓烈的游戏意味，于是将大正方形比小正方形大的面积转化为一个长5.5米、宽4.5米的长方形的面积：5.5 × 5.5 - 4.5 × 4.5 = （5.5 + 4.5） × （5.5 - 4.5） = 10 × 1 = 10（平方米）。

这样的游戏活动，建立于学生玩拼图、玩七巧板等游戏活动的基础上，虽然拼的过程中只是某个部分的图形位置变化，但是整个图形的面积不变，既巩固了周长与面积的知识，又启迪学生灵活运用数形直观，将复杂的运算变得简单化！直观图的应用，让学生豁然开朗。通过将原来的图形剪一剪、拼一拼，学生一下子看出了结果，发现了隐藏的规律，这为学生今后学习两个数的平方的差与两数之和、两数之差的关系：a2 - b2 = （a + b）（a - b）奠定了坚实的基础。当数与形有机结合时，复杂的运算有时变得非常简单，这就是数学特有的魅力！数学眼光顷刻间在这有趣的直观几何中得到培养。

四、于游戏中打通联系，倾力于“提炼表达”

培育数学眼光的过程，就是一个打通数学与真实生活之间联系的过程，或者说，数学眼光就建立在这种“联系”的基础之上。

学生的游戏生活丰富多彩，数学新课标倡导学生参加跨学科学习。当下，让学生参加力所能及的劳动已经势在必行。在學校的劳动社团中，一位老师组织学生开展“烹饪小巧手”比赛活动，各个小组提供相同的材料，学生在炒菜的过程时而加盐，时而加水，时而盖起锅盖加热，劳动场面可谓是热火朝天！劳动比赛结束后，评委们尝一尝菜肴，分别量分评比，第一个游戏环节结束。评委们又进行了第二轮闯关抢答评分，老师让各小组学生进行了闯关比赛，抢答后，教师组织学生进行语言表达，判断推理。

闯关一：炒菜时，第一组向锅里加了一些盐，这时菜就变得咸一些。选择（  ）时，可以解释这样的现象。（a表示原来的盐水，b表示原来的盐，m表示加入的盐。）

闯关二：炒菜时，第二组向锅里加了一些水，这时菜就变得淡一些。选择（      ）时，可以解释这样的现象。（a表示原来的盐水，b表示原来的盐，m表示加入的盐。）

闯关三：炒菜时，第三组将锅盖盖上，煮了几分钟后，这时菜变得咸一些。选择（   ）时，可以解释这样的现象。（a表示原来的盐水，b表示原来的盐，m表示加入的盐。）

炒菜比赛是一种劳动，也是一种游戏。将生活中最为常见的炒菜赋予游戏的意义与价值。一方面，学生沉醉于快乐的炒菜活动，享受劳动的乐趣；另一方面，教师又通过更高层次的闯关活动，启迪学生用数学语言解释生活现象，打通生活与数学的关联，融合百分率（含盐率）、分数大小比较、用字母表示数等知识点，建构加盐变咸、加水变淡、加热变咸等烹饪情境下的多样化的数学模型。学生的数学眼光于语言提炼、模型表达的过程中自然形成，这更加有利于学生认识到：生活中处处有数学，数学与生活紧密联系，同时，更好地促进学生对真实的生活进行数学化的语言提炼与表达。

五、于游戏中激活想象，发力于“数趣探奇”

游戏往往具有丰富的想象和创造空间。教师可以巧妙设计游戏活动，让学生认识“数趣”之奇妙，在“数趣探奇”活动中发力，从而更好地培育学生的数学眼光。

教学一个数的因数后，有一位教师设计了这样的游戏：

游戏要求：（1）找一找：220和284的因数，看谁找得快！

（2）算一算：将每个数除去本身以外的所有因数相加。

（3）比一比：你有什么发现？将你的发现取个好听的名字。

学生在正确、迅速找到一个数的因数的过程中，体验活动的乐趣！学生通过计算发现：220的因数（本身除外）相加：1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284；284的因数（本身除外）相加：1 + 2 + 4 + 71 + 142 = 220。

在这样的游戏活动中，学生一方面熟悉找一个数的因数的方法，加深对一个数的最大因数是它本身的认识；另一方面，它们惊奇地发现，220除去它本身的所有因数的和等于284，而284除去它本身的所有因数的和等于220。

学生的好奇心一下子被激活，教师继续进行游戏比赛：试一试，看哪个小组能够找到第二对这样的数！教室顿时沸腾起来，小组成员有的猜想，有的列举，忙着找一个数的因数（本身除外）并求和。时间一分一秒地过去了，教室里安静下来！所有的小组都以失败告终，于是，有的小组认为：220和284纯属巧合，不可能再有第二对了！还有的小组认为：给我们足够的时间，一定会找到！更有的小组认为：可能会有某种规律存在，随着数越来越大，一定会出现不少这样的数……游戏虽然没有结论，但给学生留下无尽的遐想。

为了满足好奇心、探究心，接着，教师于学生悱愤之际，给出自主阅读材料：古希腊的数学家给这样的两个数起名为“相亲数”，也就是，彼此的全部因数（本身除外）之和都与另一方相等。17世纪法国数学家费马找到了第二对“相亲数”——17296和18416，同一时期，另一位法国数学家笛卡尔找到了第三对“相亲数”——9363544和9437056。目前，找到的“相亲数”已经超过1000对[3]。“相亲数”究竟有多少对呢？它们的分布有规律吗？直到今天，数学家也没有得出一个确定的答案。

对学生而言，以上的游戏活动是有意义的，即使第二个游戏活动学生未能找到具体的答案，但学生是在积极体验求一个数的因数的过程，同时也在探索的过程中想象、发现，在阅读的活动中感受数的奇趣。在游戏中想象，在数趣中感悟，学生数学眼光的培养更加深刻、有效。

数学游戏，儿童学习数学的核心方式。教师要精巧设计丰富多样的数学游戏，通过问题驱动、经验积累、几何直观、提炼表达、数趣探奇等鲜活、生动的体验活动，让数学游戏在深度学习中展现其趣、其理、其乐，让学生的数学眼光在智趣活动中得到有效培育，从而达成学生数学核心素养创新发展的至高境界！

[参 考 文 献]

[1]中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022：5.

[2]史宁中.曹一鸣.义务教育数学课程标准（2022年版）解读[M]北京：北京师范大学出版社，2022：46.

[3]魏红霞.学习改变未来.趣味数学[M]北京：北京教育出版社，2014：38-39.

（责任编辑：杨红波）