基于混沌宿主切换机制的䲟鱼优化算法

贾鹤鸣，力尚龙，陈丽珍，刘庆鑫，吴 迪，郑 荣

（1.三明学院 信息工程学院，福建 三明 365004；2.海南大学 计算机科学与技术学院，海口 570228；3.三明学院 教育与音乐学院，福建 三明 365004）

0 引言

基于群体智能的元启发式优化算法能够有效地解决具有非线性、高纬度和目标函数不可导的全局优化问题［1-2］，但是，NFL（No-Free-Lunch）理论也证明不存在一种能解决所有问题的优化算法［3］。目前，诸多元启发式算法被提出，如正余弦算法（Sine Cosine Algorithm，SCA）［4］、飞蛾优化算法（Moth-Flame Optimization algorithm，MFO）［5］、鲸鱼优化算法（Whale Optimization Algorithm，WOA）［6］、乌燕鸥优化算法（Sooty Tern Optimization Algorithm，STOA）［7］、哈里斯鹰优化算法（Harris Hawks Optimization algorithm，HHO）［8］、黏菌优化算法（Slime Mould Algorithm，SMA）［9］、精子群优化算法（Sperm Swarm Optimization algorithm，SSO）［10］、爬行动物搜索算法（Reptile Search Algorithm，RSA）［11］，并利用它们解决不同复杂程度的全局优化问题［12］。

䲟鱼优化算法（Remora Optimization Algorithm，ROA）［13］是一种新的基于仿生学的元启发式优化算法。它主要模拟了海洋生物䲟鱼的生存狩猎方式，是通过建模䲟鱼依附宿主、经验攻击和宿主觅食等过程而设计的一种优化方法。ROA 原理简单，探索能力与开发能力都较强，但由于通过经验攻击切换宿主，导致探索与开发之间平衡性较差、求解精度较低并且容易陷入局部最优。基于上述问题，众多学者对ROA 进行改进，例如：Zheng 等［14］提出了一种融入自主觅食机制的䲟鱼优化算法，通过一种概率选择的䲟鱼自主觅食机制，增强原算法的探索能力；Liu 等［15］提出了一种融合多策略的䲟鱼优化算法，引入布朗运动增强算法的全局探索能力，再利用透镜成像反向学习策略增强跳出局部最优的能力，实现改进算法探索和开发能力之间的有效平衡。Tent 混沌映射是现有混沌映射中的一种，具有随机性、遍历性和有序性的特点，能够有效改善优化算法的分布随机性问题［16］。腾志军等［17］提出了一种基于Tent 映射的混合灰狼优化的改进算法，通过Tent 混沌映射产生初始种群，增加初始种群个体的多样性。周鹏等［18］提出了基于阶梯式Tent 混沌和模拟退火的樽海鞘群算法，引入Tent 混沌映射初始化种群，提高算法在迭代前期的收敛速度。

受上述两种ROA 的改进思想和Tent 混沌映射策略运用的启发，本文提出一种基于改进宿主切换机制的䲟鱼优化算法（Modified ROA，MROA）。针对原始ROA 宿主切换机制存在的问题，设计一种新的宿主切换机制，使宿主的切换更加合理，从而更好地平衡算法的探索和开发能力；同时，为了使䲟鱼初始宿主多样化，引入Tent 混沌映射初始化种群，进一步优化算法的性能。通过上述两种改进方法，使探索与开发基本得到平衡，提高ROA 寻优能力、收敛能力和跳出局部最优的能力。选取CEC2020 测试函数［19］验证算法性能，同时选取了两个典型工程问题进行测试，实验结果印证了本文算法的有效性和工程实用性。

1 䲟鱼优化算法

䲟鱼优化算法［13］是受䲟鱼寄生行为启发的一种优化算法。旗鱼是海洋中速度最快的鱼类，通常采用群体狩猎的模式，旗鱼的狩猎方式为轮流攻击的精英战术。座头鲸体型庞大，经常独自捕食。当䲟鱼吸附在宿主（旗鱼、座头鲸）身上时，可以认为䲟鱼的位置是随着宿主位置的改变而改变的。基于这种思想，䲟鱼优化算法中采用了旗鱼优化算法和鲸鱼优化算法中的运动公式作为䲟鱼的运动公式［13］。此外，䲟鱼还会围绕宿主做小范围的移动，依靠“经验攻击”尝试捕食。当周围食物变少时，䲟鱼会判断是否需要更换宿主。如果不改变宿主，则通过“宿主觅食”策略获取食物。

1.1 自由旅行（探索阶段）

1.1.1 旗鱼优化策略

䲟鱼优化算法的探索阶段被命名为“自由旅行”。当䲟鱼吸附在旗鱼上时，可以认为䲟鱼的位置随旗鱼的改变而同步改变。基于旗鱼优化算法的精英思想，改进原本的旗鱼位置更新公式，数学模型如式（1）所示：

其中：t代表当前迭代次数；i代表第i个个体；Ri（t+1）代表更新后的个体位置；RBest（t）为更新前的最优个体位置；rand为［0，1］的随机向量；Rrand（t）代表更新前随机个体的位置。

1.1.2 经验攻击

为了确定是否需要更换宿主，䲟鱼会围绕宿主不断进行小范围移动，这个过程类似经验的积累。该思想的数学模型如式（2）所示：

其中：Ri（t）代表个体当前位置，Rpre（t）代表上一次迭代的位置，这可以看作是一种经验。Ratt（t+1）代表䲟鱼试探性的一步。该机制首先利用randn函数的随机性在当前位置和上一位置之间进行局部搜索；然后通过比较当前位置的适应度值和试探移动后的适应度值判断是否需要更换宿主。

1.2 细细品味（开发阶段）

1.2.1 鲸鱼优化策略

在开发阶段，䲟鱼则吸附在座头鲸表面，这一阶段被命名为“细细品味”。当䲟鱼的宿主是座头鲸时，其位置更新方程如式（3）所示：

其中：e 为自然常数；D代表宿主与猎物之间的距离，计算公式如式（4）；l为［-1，1］的随机数，用于构造螺旋体，计算公式如式（5）；a为螺旋体的控制系数，在迭代过程中会在［-2，-1］内线性下降，计算公式如式（6）：

其中：t为当前迭代次数，T代表最大迭代次数。

1.2.2 宿主觅食

宿主觅食策略进一步细分搜索空间，在此阶段，最佳解的空间可以缩小为宿主的位置空间。此时䲟鱼在宿主周围进行小范围移动：

其中A代表䲟鱼的移动步长，A值与䲟鱼和宿主的体积空间有关，计算公式如式（8）：

其中：C为䲟鱼因子，用于映射䲟鱼的位置，本文选用0.1；B用来模拟䲟鱼寄宿的空间，计算公式如式（9）：

其中V代表䲟鱼的体积，计算公式如式（10）：

2 改进䲟鱼优化算法

2.1 Tent混沌初始化

与大多数元启发式算法一样，原始ROA 使用随机产生的数据初始化种群，这种初始化方法无法确保种群的多样性。与基本随机方法不同，混沌映射具有遍历性和有序性。因此，采用混沌映射序列初始化种群能够最大限度维持种群的多样性，增强算法全局搜索的能力。鉴于多种混沌映射序列的分布情况不同，本文选用了Tent 混沌映射序列［18］进行种群初始化。Tent 混沌映射序列的表达式如式（11）：

为了展示基本随机方法与Tent 混沌映射序列对种群初始化的影响，本文给出基本随机种群初始化与Tent 混沌映射种群初始化在二维平面的示例，如图1 所示。显然，基本随机方法在种群规模较小的情况下无法维持种群的多样性，而Tent 混沌映射序列较好地解决了这一问题。

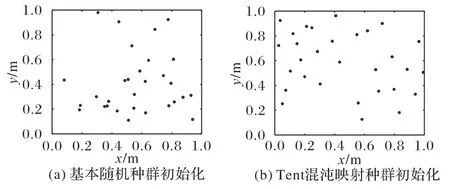
图1 两种种群初始化方法在二维平面的示例Fig.1 Examples of two population initialization methods in two-dimensional plane

2.2 宿主切换机制

原始ROA 通过对比经验攻击前后位置的适应度值判断是否更换宿主。经验攻击是基于上一次迭代后的位置和宿主当前位置决定的，并且䲟鱼寻找食物需要依赖宿主，它本身并不具备良好的觅食能力。这种宿主更换方法导致䲟鱼频繁更换宿主，当算法陷入局部最优后这一问题会变得更加显著，大幅降低了算法的寻优性能。

为了解决上述问题，本文提出一种新的宿主切换机制。即䲟鱼在宿主周围进行经验攻击后，评估一次宿主周围环境，根据评估结果选择是否更换宿主。新的宿主切换机制大幅降低了䲟鱼自身觅食能力的影响，提高了算法的寻优性能。

其中：Rnew是宿主附近的一个新位置；k是一个随机移动因子，用于限制评估的范围，计算公式如式（13）；step表示移动的步长，计算公式如式（14）：

其中：β用于控制移动因子，本文选用0.6。

其中Rr1（t）、Rr2（t）是种群中两个随机个体更新前的位置。

通过对比宿主位置及其附近新位置的适应度值，决定是否更换宿主。同时为了更好地解决频繁更换宿主的问题，引入线性递减的动态因子P，计算公式如式（15）：

在迭代前期由于所处区域食物匮乏，䲟鱼为了更好地生存会频繁评估宿主；在迭代后期进入食物丰富的区域后，由于食物充足，䲟鱼也会减少对宿主的评估，这样的改进就更加符合䲟鱼的生活习性。

2.3 MROA伪代码

MROA 的流程如图2 所示。MROA 描述如下。

图2 MROA的流程Fig.2 Flow of MROA

3 实验与结果分析

本文实验均在主频为2.50 GHz 的11th Gen Intel Core i7-11700 处理器，16 GB 内存，操作系统在64 位Windows 11 的电脑上使用Matlab 2021a 完成。为了验证MROA 的性能，本文采用了CEC2020 测试函数［19］进行仿真实验。CEC2020 测试函数的详细介绍如表1 所示，函数的搜索范围均为［-100，100］。

表1 CEC2020测试函数Tab.1 CEC2020 test functions

3.1 参数设置

本文选取了ROA［13］、RSA［11］、WOA［6］、HHO［8］、SSO［10］、SCA［4］和STOA［7］作对比，验证改进算法的优越性。本次实验设置的参数有：空间维度Dim=10，最大迭代次数T=500，种群规模N=30。选取30 次运行的最优适应度值、平均适应度值、适应度值标准差、收敛曲线和15 次运行的Wilcoxon 秩和检验的实验结果作为评价指标。各对比算法参数设置如表2所示。

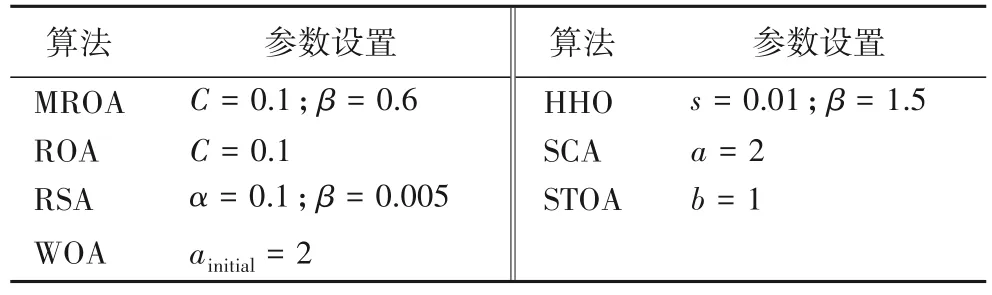
表2 不同算法参数设置Tab.2 Parameter setting of different algorithms

3.2 求解精度分析

MROA 和对比算法的最优适应度值（Best）、平均适应度值（Mean）和适应度值标准差（Std）如表3 所示。

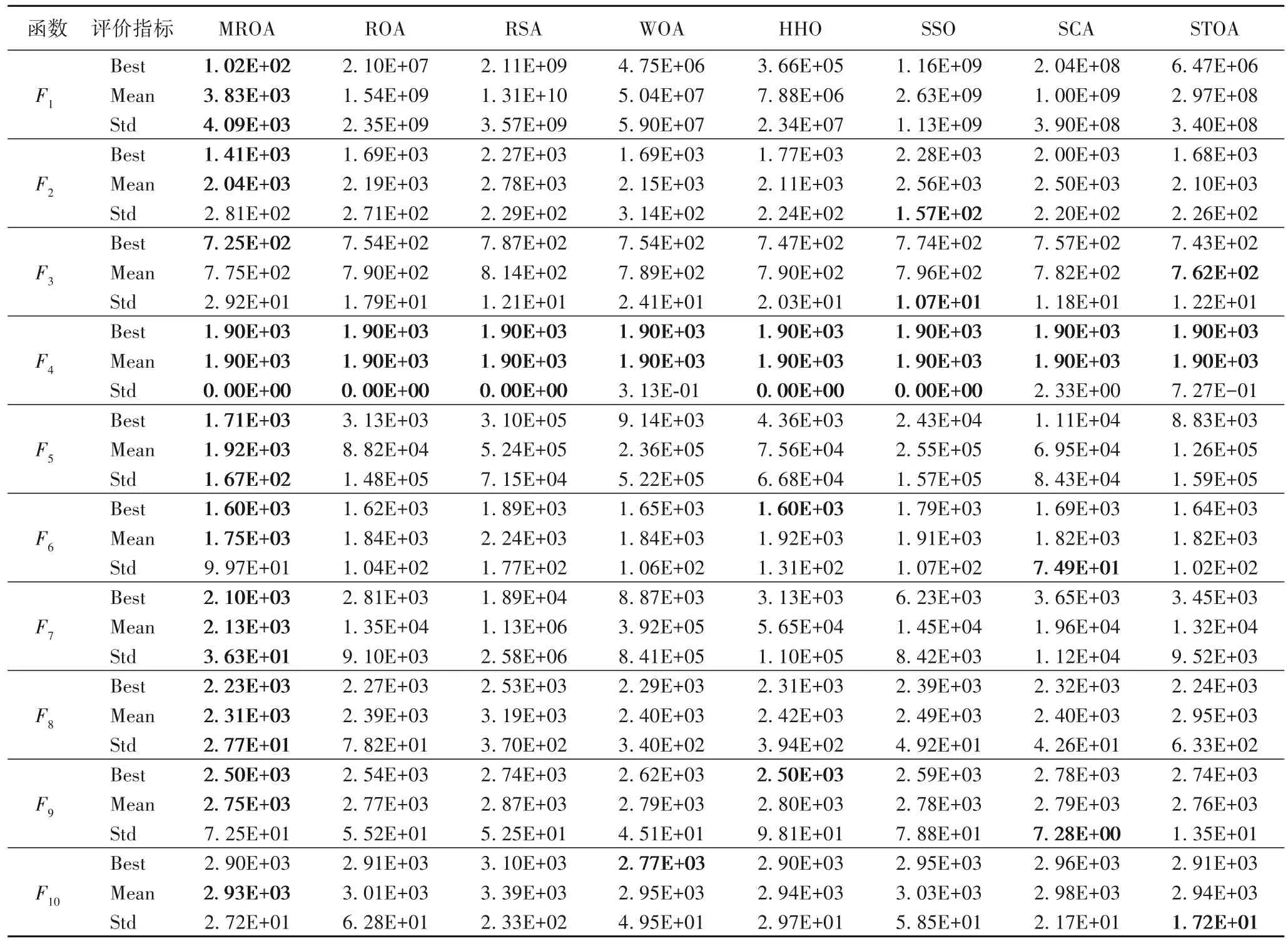
表3 不同算法在CEC2020函数上的测试结果Tab.3 Test results of different algorithms on CEC2020 test functions

F1为单峰函数，MROA 在F1中取得了最佳的最优适应度值、平均适应度值和适应度值标准差，明显优于ROA 和其他对比算法。可以看出MROA 在单峰函数中明显更优。F2、F3为多峰函数，MROA 在F2和F3中都取得了最佳的最优适应度值，在F2中也取得了最佳的平均适应度值。ROA、WOA、HHO 以及STOA 在F2中取得的平均适应度值与MROA 相差不大，但是最优适应度值明显较差，表明MROA 有着较强的跳出局部最优的能力。SSO 在F2中取得了最小的适应度值标准差，但最优适应度值和平均适应度值明显很差。STOA在F3中取得了最好的平均适应度值，MROA 和SCA 取得的平均适应度值与之相差较小，可以看出MROA 在F3中依然表现出了较好的跳出局部最优的能力，但稳定性略逊一筹。SSO在F3中依然取得了最小的适应度值标准差，平均适应度值与其他算法相差不大，但最优适应度值明显较差，表明SSO 在多峰函数中明显较差，而MROA 在多峰函数中依然表现出更好的寻优能力。F4为无峰函数，除WOA、SCA 和STOA 可能找不到理论最优值外，其他对比算法都可以稳定地找到理论最优值。F5、F6、F7为混合函数，MROA 在F5、F6和F7中都取得了最佳的最优适应度值和平均适应度值。F5和F7中MROA 也取得了最小的适应度值标准差，明显优于ROA 以及其他对比算法。F6中HHO 同样取得了最佳的最优适应度值，ROA、WOA 和STOA 取得的最优适应度值与之差距较小，但与HHO 一样，平均适应度值与MROA 相差较大；SCA 算法取得了最小的适应度值标准差，但最优适应度值和平均适应度值明显较差，可以看出在F6中MROA 明显更优。显然MROA 在混合函数中表现出了更好的鲁棒性。F8、F9、F10为复合函数，MROA 都取得了最好的平均适应度值，在F8和F9中也都取得了最好的最优适应度值，F8中MROA 取得的适应度值标准差同样最小。HHO 在F9中同样取得了最好的最优适应度值，但平均适应度值劣于MROA。SCA 在F9中取得了最小的适应度值标准差，平均适应度值也与MROA 相差较小；但最优适应度值明显很差，显然陷入了局部最优且无法跳出。在F10中WOA 取得了最佳的最优适应度值，但平均适应度值仅仅略差于MROA，显然WOA 在F10中稳定性略差。MROA 在复合函数中的寻优能力明显更优。经计算MROA在CEC2020 测试函数中取得的最优适应度值、平均适应度值?和适应度值标准差分别平均比其他对比算法提高了28%、33%和12%。

3.3 收敛曲线

收敛曲线能够更为直观地展示算法的寻优能力，因此本文给出MROA 和对比算法在CEC2020 测试函数上的收敛曲线，如图3 所示。

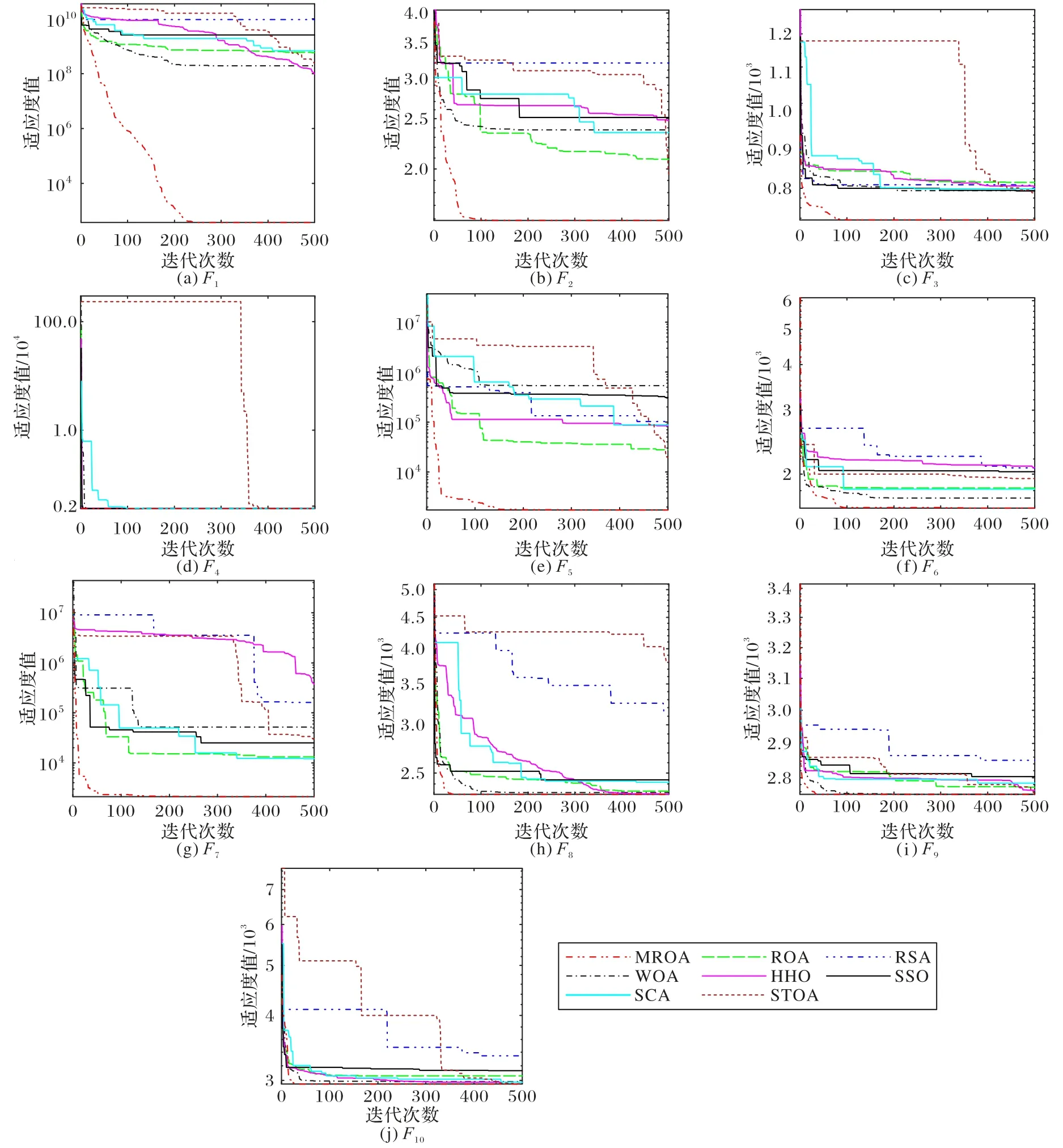
图3 CEC2020测试函数各算法收敛曲线Fig.3 Convergence curves of various algorithms for CEC2020 test function

在单峰函数F1中，MROA 能较快收敛，而对比算法无法收敛。在多峰函数F2、F3中，MROA 在迭代前期已经找到较优值，ROA 和STOA 表现出了一定的跳出局部最优的能力，但收敛不足，而其他对比算法均陷入局部最优。对于无峰函数F4，SCA 和STOA 表现出较差的寻优能力。在混合函数F5、F6和F7中，MROA 依然在迭代前期找到了较优值。在F5中，STOA 能够跳出局部最优，但收敛较差，而其他对比算法均陷入局部最优；在F6中，WOA 和MROA 一样在迭代前期快速收敛，但MROA 收敛能力明显更优；对于F7，RSA、HHO 和STOA较早陷入局部最优，但展现了一定的跳出局部最优的能力，其他对比算法也在收敛到一定程度后陷入局部最优并无法跳出。在复合函数F8、F9、F10中，MROA 同样展现了更优的收敛能力。F8中WOA 收敛略慢，ROA 次之，SSO 和SCA 在收敛到一定程度后陷入局部最优，HHO 虽然收敛较慢但没有陷入局部最优，RSA 和STOA 则较早地陷入局部最优导致无法收敛。在F9中WOA 依然收敛略慢，而其他对比算法均陷入局部最优，只有HHO 和STOA 在迭代后期成功跳出局部最优。对于F10，WOA 仍然收敛略慢，ROA、HHO 和SCA 次之，RSA 和STOA 陷入局部最优，而STOA 在多次陷入局部最优后依然能够跳出。

3.4 Wilcoxon秩和检验

仅通过对最优适应度值、平均适应度值、适应度值标准差和收敛曲线的分析，不能精确地分析算法的性能。因此本文采用Wilcoxon秩和检验验证MROA和对比算法整体结果的显著差别［20］。其中，显著水平为5%，当p值小于5%时，表明对比双方存在显著差异，反之比较接近［21］。本文在CEC2020 中独立运行15次得到实验结果，统计结果如表4所示。

表4 不同算法在Wilcoxon秩和检验中的结果Tab.4 Results of different algorithms in Wilcoxon rank-sum test

如表4 所示，在F4中存在较多值为0 的结果，这是因为CEC2020 中的F4相对简单，多数算法都可以很快取得最优值。在F10中也存在值大于5%的情况，这表明在F10中MROA与WOA 在寻优能力上没有明显的差异。而在其他的测试函数中得到的结果都是p值小于5%，可以证明MROA 在大多数测试函数中与对比算法存在显著差异，且明显优于对比算法。通过Wilcoxon 秩和检验，可以得出MROA 在CEC2020 测试函数中表现出了较好的寻优性能的测试结论。

通过对30 次运行的最优适应度值、平均适应度值、标准差、算法收敛曲线和15 次运行的Wilcoxon 秩和检验的分析，充分说明原始ROA 由于宿主切换机制不够合理，导致探索与开发平衡较差，存在收敛不足、跳出局部最优能力不足的问题，而MROA 在改变宿主切换机制同时引入Tent 混沌初始化，解决了探索与开发不平衡的问题，有效地增强了算法的寻优能力。

3.5 计算时间分析

为了展示MROA 的计算成本，记录了在CEC2020 测试函数中各算法的计算时间，统计结果见表5。虽然MROA 与ROA 具有相同的计算复杂度，但实验数据表明MROA 的计算时间成本大于ROA。这是因为本文提出的宿主切换机制需要进行宿主评价和选择，会进行多次额外的适应度值计算，导致MROA 的运行时间明显较长。此外，考虑到NFL 定理，增加计算时间以获得更为可靠的解是可以接受的。

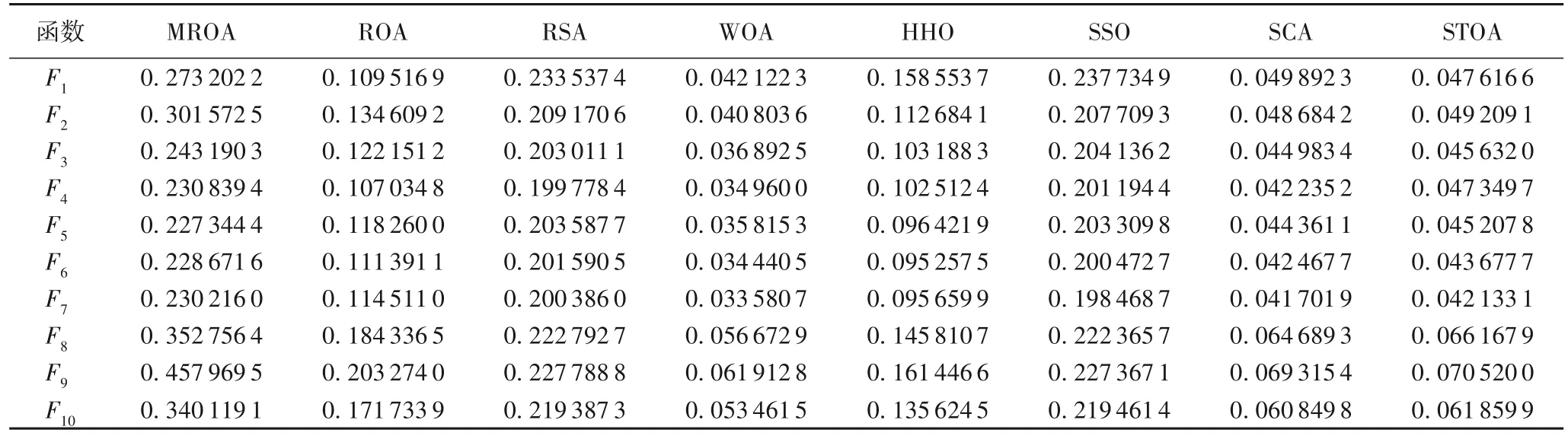
表5 CEC2020测试函数上不同算法的计算时间 单位：sTab.5 Computational time of different algorithm on CEC2020 test functions unit：s

3.6 参数敏感性分析

MROA 增加的参数只有β，参数β的作用是控制随机因子，对MROA 的性能影响较大。本文选取β=0.1～0.9 进行实验，记录当β选取不同数值时，MROA 在CEC2020 测试函数中独立运行30 次的平均值。实验结果如表6 所示，当β=0.6 时MROA的性能显然更优，β=0.8时次之。

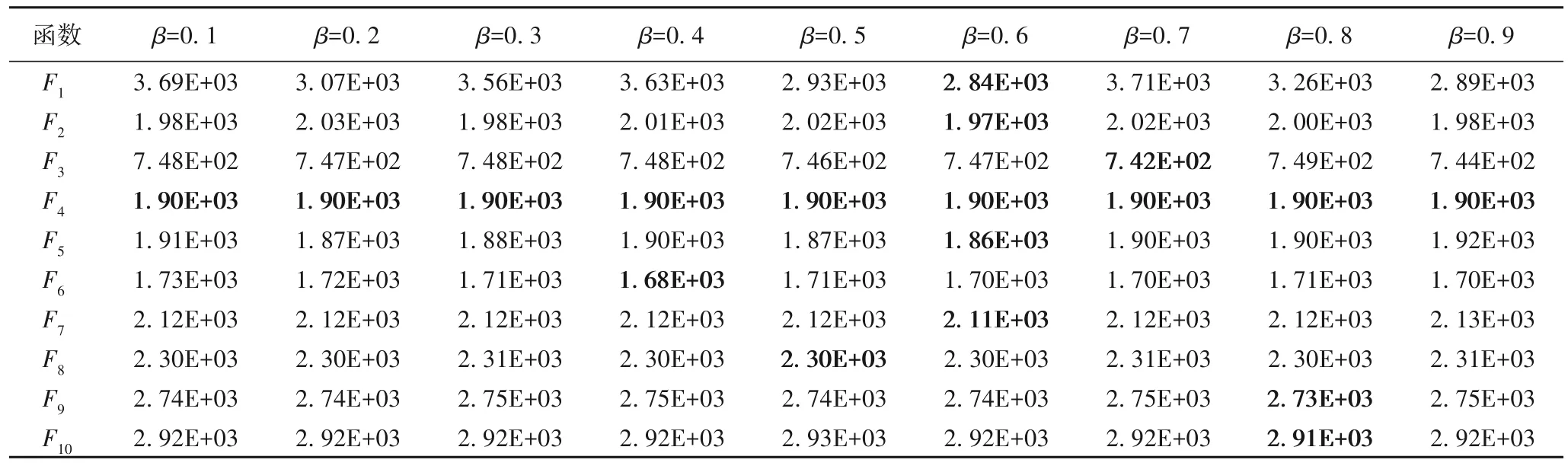
表6 参数敏感性分析Tab.6 Parameters sensitivity analysis

4 工程问题

实际问题的应用是算法研究的目的之一，在测试函数中的结果并不能完全体现算法在实际问题中的性能。为了验证MROA 在实际问题中的适用性，本文选择了焊接梁设计问题和多片式离合器制动器设计问题进行实验和测试。

4.1 焊接梁设计问题

焊接梁设计问题的目的是在7 个约束条件的限制下求出成本最小的焊接梁的4 个相关参数，具体模型如图4［12］。关键参数分别为剪切应力τ、横梁弯曲应力σ、屈曲载荷Pc、衡量挠度δ和相关参数的约束。4 个相关参数分别为焊缝宽度h、横梁宽度t、横梁长度l和横梁厚度b。

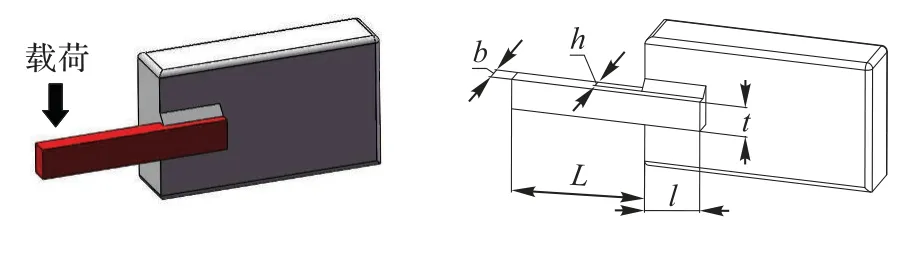
图4 焊接梁设计问题模型Fig.4 Welded beam design problem model

焊接梁设计问题数学模型如下：

目标函数：

约束条件：

变量范围：

其他参数：

表7 是几种算法在焊接设计问题中求得的解。其中ROA、MFO、GWO（Grey Wolf Optimizer）、MVO（Multi-Verse Optimization）、WOA、CPSO（Co-evolutionary Particle Swarm Optimization）、RO（Ray Optimization）的 结果来源于文献［13］。MROA 在焊缝宽度为0.205 740、横梁长度为3.253 000、横梁宽度为9.036 600 以及横梁厚度为0.205 730时得到了最小的成本1.695 200。其中焊缝宽度最大，横梁长度最小，横梁宽度和横梁厚度适中，最终得到的成本相较于其他对比算法明显更小。MROA 在焊接梁设计问题上明显具有更优的性能。

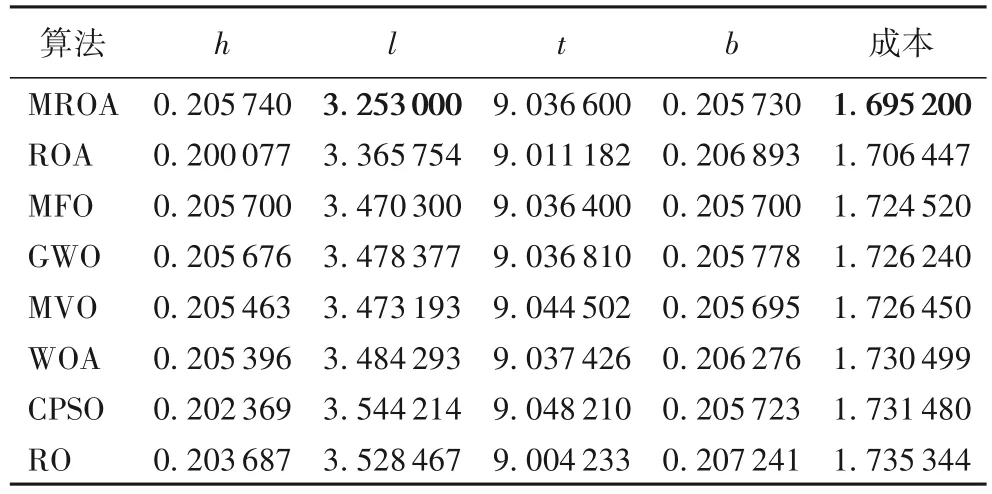
表7 不同算法在焊接梁设计问题中的实验结果Tab.7 Experimental results of different algorithms in welded beam design problem

4.2 多片式离合器制动器设计问题

多片式离合器制动器设计问题的目的是在8 个约束条件的限制下求出质量最小的多片式离合器制动器的5 个相关参数，具体模型如图5［11］所示。5 个相关参数分别为内半径ri、外半径ro、圆盘厚度t、驱动力F和摩擦表面数量Z。

图5 多片式离合器制动器设计问题模型Fig.5 Multi-plate clutch brake design problem model

多片式离合器制动器设计问题数学模型如下：

目标函数：

约束条件：

变量范围：

其他参数：

表8 是不同优化算法在多片式离合器制动器设计问题中求得的解。其 中 TLBO（Teaching Learning Based Optimization）、WCA（Water Cycle Algorithm）、MVO、CMVO（Chaotic Multi-Verse Optimization）、MFO、RSA 的结果来源于文献［11］。MROA 在内半径为70、外半径为90、圆盘厚度为1、驱动力为600 和摩擦表面数为2 时得到了最小的质量0.235 24，明显性能更优。

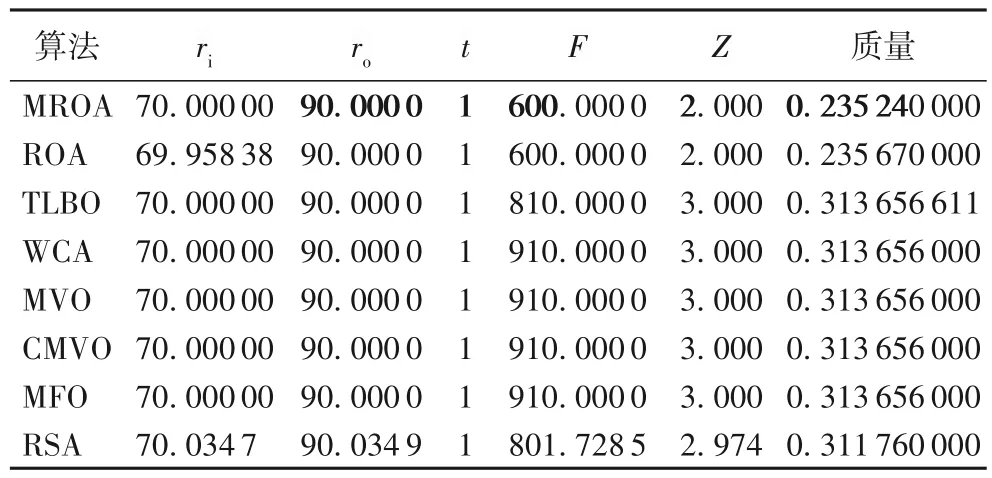
表8 不同算法在多片式离合器制动器设计问题中的实验结果Tab.8 Experimental results of different algorithms in multip-plate clutch brake design problem

通过对上述两种工程问题的求解，进一步证明了原始ROA 的不足，并验证了本文所提改进方法的有效性。MROA在实际的工程问题中能够找到更优的解，验证了MROA 在实际工程问题中具有较高的应用价值。

5 结语

本文针对ROA 由于通过经验攻击进行宿主切换，导致探索与开发之间平衡较差、求解精度较低并且容易陷入局部最优的问题，提出一种新的宿主切换机制，同时引入Tent 混沌映射初始化种群。通过上述改进使探索与开发基本平衡，增强寻优能力、收敛能力和跳出局部最优的能力。利用CEC2020 对算法性能进行了测试验证，实验结果表明MROA在不同函数中都表现出更好的鲁棒性。同时，通过求解焊接梁设计问题和多片式离合器制动器设计问题，进一步验证了MROA 在实际工程问题中的适用性。在未来的工作中，计划把本文算法应用至其他实际问题例如特征选择和多阈值图像分割，进一步探讨本文算法的优化性能。