面向场面运行效率提升的离场航班调度优化

何玉建,胡明华,*,袁立罡

(1. 南京航空航天大学民航学院,江苏 南京 211106;2. 国家空管飞行流量管理技术重点实验室,江苏 南京 211106)

1 引言

随着民航的快速发展,航空运输业的需求也逐年迅速增长,随之而来的航班延误,终端区拥挤、场面滑行冲突等问题制约了空中交通的正常运行,如何在有限的空域容量内满足空中交通流量的需求是亟需解决的问题,机场作为航班运行保障的主体单位,其运行效率和保障水平很大程度上影响了空中交通运行整体水平,因此充分利用机场有限的资源,合理调度航班起降,有效提升航班服务保障是解决现阶段民航发展过程中所遇到的问题的关键手段。目前我国大多数机场为多跑道配置,多跑道作为制约大型繁忙机场起降航班的重要瓶颈区,科学调度航班流量对于促进多跑道协同运行、提高机场运行效率、保障航班安全具有重要意义。

关于跑道调度问题国内外积累了一定的研究成果,针对单跑道运行下航班排序,Desai[1]和ÇEÇEN[2]以航班延误最小为目标函数建立了混合整数线性规划模型。Malik采用多目标动态规划算法[3]、张军峰采用多目标帝国竞争算法[4]分别对跑道调度问题进行求解。江灏改进了已有文献中评估航空公司延误公平性的目标函数,满足了不同利益相关方的需求[5]。针对多跑道运行条件下航班排序,Hancerliogullari将航班调度问题建模为并行的机器调度问题,并采用启发式算法进行求解[6]。Chandrasekar和王菲采用分支定界方法来优化航班进离场排序[7]。尹嘉男考虑了绿色机场发展理念,并将最小化环境污染作为优化目标函数之一[8]。针对多机场终端区运行条件下的进离场交通流排序,马园园提出了“航班满意度”的概念[9],葛腾腾采用了改进模拟退火算法对进离场排序模型进行求解[10]。Liu将两阶段无等待混合流水车间模型应用于多机场调度问题[11],Zhong考虑了不同航班流向的延误差异,设计了自适应禁忌搜索算法对所建立的多目标整数规划模型进行求解[13]。

已有研究针对跑道调度问题取得了一定的成果,但是并没有考虑起飞跑道与停机位的位置关系,针对于航站楼位于两条或者多条跑道中心的机场来说,尽量减少航班在场面的滑行时间对于提高场面运行效率至关重要,因此本文从减少场面运行时间角度来优化离场航班排序。

2 多跑道离场航班调度优化模型

2.1 问题描述

多跑道离场航班调度是指根据预期的离场交通流需求,考虑停机位,跑道配置,天气因素等条件对离场航班起飞时间以及顺序进行优化,优化的同时要尽量满足空管、机场以及航司的诉求,实现科学合理安排最优起飞时间、离场顺序以及跑道,使其调度时间段内机场运行总效率最高,航班总延误成本最小,航班调整次序变动最少的目的。

2.2 模型建立

假设调度时间段内离场航班集合为F,非受控离场航班集合为FN,受控离场航班集合为FC,起飞跑道集合为R。

2.2.1 模型假设

1)研究时段内的离场航班停机位信息和航班计划起飞时间等信息是已知的;

2)航班离场排序过程中,每架航班只能分配一个时隙;

2.2.2 目标函数

为了符合机场协同决策的理念,考虑了空管、机场和航司三方的利益诉求,从航班延误、跑道运行能力以及跑道就近分配三个角度建立优化目标。

1)最小化离场航班总延误

将所有离场航班按照是否受流控影响分为受控离场航班和非受控离场航班,受控离场航班延误根据《民航航班正常性统计办法》来计算,非受控航班延误等于优化起飞时间与计划关舱门时间和标准地面滑行时间之和的差值的绝对值。

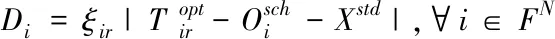
(1)

针对于受控航班,全国流量管理系统会以航班计划为基础,依据流量管理措施和航班优先级为受控航班分配计算起飞时间(Calculated Take Off Time,CTOT)。受控航班须在发布的计算起飞时间前后一定容差范围内起飞,根据《中国民航空管流量管理运行规则》:CTOT时隙容差分为一类和二类容差,基于容量管理的流量管理措施为一类容差,容差范围为(-5,10)分钟;基于间隔管理的流量管理措施为二类容差,容差范围为(-3,3)分钟,为了尽量保障受控航班符合CTOT运行,将受控航班离场延误定义为优化起飞时间与CTOT差值的绝对值

(2)

考虑到受控航班相比于非受控航班具有更大的优先级,可以对受控离场航班的延误赋予更大的权重,重点保障受控离场航班CTOT的准点率,因此调度时间段内离场航班总延误定义为

(3)

式中:α为受控离场航班延误权重

2)最大化跑道容量

将调度时间段内所有起飞跑道容量最大作为目标进行优化,它近似等于调度时间段内最后一架起飞航班的优化起飞时间与第一架离场航班的优化起飞时间之差,即

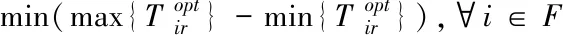
(4)

3)最小化跑道分配

大多数机场都是远距平行跑道,航站楼位于两条跑道中间或者一侧,停机位处于航站楼附近,为了降低场面运行时间,考虑离场航班机位与跑道之间的距离,以就近分配跑道原则作为优化目标,即

(5)

2.2.3 约束条件

离场航班调度考虑的约束条件主要有:唯一性约束、尾流间隔要求、时间窗约束以及最大约束位置转换约束。

1)跑道唯一性约束

调度时间段内每架离场航班只允许分配一条起飞跑道,即

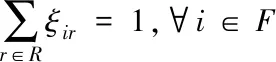
(6)

2)尾流间隔约束

φij+φji=1

(7)

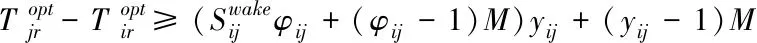
(8)

yij≥ξir+ξjr-1

(9)

yij≤(ξir+ξjr)/2

∀i,j∈F,且i≠j

(10)

约束(7)限制离场航班i和航班j前后顺序的唯一性,约束(8)为尾流间隔约束,限制同一跑道起飞的前后航班需要保持对应的尾流间隔,约束(9)和约束(10)判断航班是否处于同一跑道,当航班i和航班j都分配给同一条跑道时,yij为1,否则为0。

3)时间窗约束

由于受控航班和非受控航班在机场地面保障有所差异,因此将时间窗约束分为受控离场航班时间窗约束以及非受控离场航班时间窗约束,每架离场航班必须在规定的起飞时间窗内完成起飞。

非受控离场航班优化起飞时间应当不早于航班预计撤轮挡时间与无障碍滑行时间之和,不能晚于航班预计关舱门时间与计划起飞时间与最大延误时间之和,即:

(11)

受控离场航班的优化起飞时间应满足在CTOT时隙容差范围内完成起飞,即

(12)

4)最大约束位置转换约束(Maximum Position Shift, MPS)

为了降低管制员负荷及考虑航空公司的利益,设定航班优化前后的调动次序不超过最大位置转换约束,即

(13)

5)其它变量/参数约束

离场航班索引、跑道索引、离场航班初始起飞次序和优化起飞次序均为正整数,即

(14)

航班起飞先后关系判定辅助决策变量以及航班跑道分配辅助决策变量均为0-1离散变量,即

ξij,φij,yij∈{0,1}

(15)

受控离场航班CTOT时隙容差上/下界的取值集合、非受控离场航班和受控航班时隙容差类别的取值集合为

∇={5,3},Δ={10,3}

(16)

vi∈{1,2}

(17)

受控离场航班延误权重、非受控离场航班的最大延误时间、尾流间隔、预计撤轮挡时间、计划关舱门时间、标准地面滑行时间、不同机位与跑道的平均滑行时间、无障碍滑行时间、计划/优化起飞时间等均为非负值,即:

(18)

3 算法设计

跑道调度问题属于典型的NP-hard问题,一般很难求解得到精确解,因此采用启发式算法多目标遗传算法(NSGA-Ⅱ)对所建立的多目标优化模型进行求解,该算法通过快速非支配排序以及拥挤距离排序可以得到综合权衡多个优化目标的Pareto最优解。

3.1 算法流程

步骤 1:确定模型相关参数;

步骤 2:读取航班信息、跑道信息、停机位信息;

步骤3:确定所有离场航班的起飞时间窗、以起飞时间窗作为基础确定决策变量的上下界,随机生成初始种群;

步骤4:解码,确定离场航班的初始离场顺序、离场时间;

步骤5:约束条件符合性检验。根据式(7)-(10)判断种群内个体是否满足间隔要求,若满足,根据目标函数计算各个目标函数的值,如果不满足,则设置个体的目标函数(M,M,M),其中M为任意大的正数;

步骤6:执行快速非支配排序以及拥挤距离计算,采用选择、交叉和变异等遗传算子操作,得到子代种群;父代种群和子代种群合并,执行快速非支配排序,生成各层级Pareto前端,通过采用拥挤算子对所有可行解进行拥挤距离排序,选取最优个体组成新的父代种群,执行种群进化迭代过程;

步骤7:若算法满足预先设定的终止条件(如达到最大进化代数),输出Pareto最优解;若否,进化代数加1,转至步骤4。

3.2 算法实现

1)非受控航班时间窗约束与MPS约束

根据文献[8],将将离场航班的最大延误时间设置为40分钟,航班最大位置转换约束为3。

2)编码与解码

将每条染色体分为空间编码片段和时间编码片段,先将以时分秒形式的时间戳格式转换为秒来表示,即将a时b分转换成秒的转换公式为:a×3600+b×60,根据离场航班的起飞时间窗,采用整数编码的方式对离场航班的优化起飞时间进行时间编码,空间编码片段亦采用整数编码对跑道号进行编码。

3)遗传算子

在算法执行过程中存在两个阶段的选择,第一次采用二元锦标赛选择,第二次根据非支配分层以及拥挤距离度量的选择方法,选择的交叉算子为模拟二进制交叉;采用的变异算子是多项式变异,由于采用整数编码,因此在进行多项式变异时候先按照实数值进行突变,然后四舍五入进行取整。

3.3 算法性能评价

从帕累托最优解的收敛性和多样性角度出发,选取以下三个多目标优化算法性能评价指标来评估模型解集的优劣。

1)世代距离(Generational Distance,GD)

GD是常用于评价多目标算法收敛性的指标,其值越小说明算法的收敛性越好,GD的计算式为

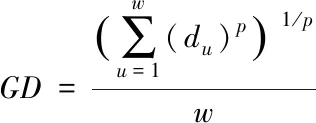
(19)

式中;w表示算法得到的帕累托前端中解的个数,p表示目标维数;du表示算法中得到的帕累托前端中每个解距离真实帕累托前端的最近欧氏距离。

2)反转世代距离(Inverted Generational Distance,IGD)

IGD可以反映多目标算法收敛性以及解的多样性,其值越小则算法的性能越好,IGD的计算式为

(20)

式中:q表示真实帕累托前端中解的个数,ds表示真实帕累托前端中每个解距离算法得到的帕累托前端的最近欧氏距离。

3)超体积(Hyper Volume,HV)

HV表示算法获得的非支配解与参照点围成的目标空间中区域的体积,HV值越大,说明算法的综合性能越好。HV的计算式为

(21)

式中:δ(·)表示勒贝格测度,用来测量体积,Vk表示第k个点与参考点围成的区域超体积。

4 实例验证

4.1 实验设计

选取国内某大型机场2020年6月3日某个时间段内的航班数据为例进行仿真验证,部分航班计划如表1所示。

表1 部分离场航班算例

综合考虑算法的运行时间和收敛效果,多次进行仿真,最终得到的算法参数为:算法最大进化代数为200;种群个体数为100;种群个体染色体长度为2|F|,交叉概率为1,变异概率为1/2|F|,分布指数为20。

4.2 结果分析

将基于先到先服务策略与本文所提的离场航班调度方法进行对比, 如图1为算法执行结束得到的不同目标函数在种群完成进化时所得到的部分Pareto最优解集。

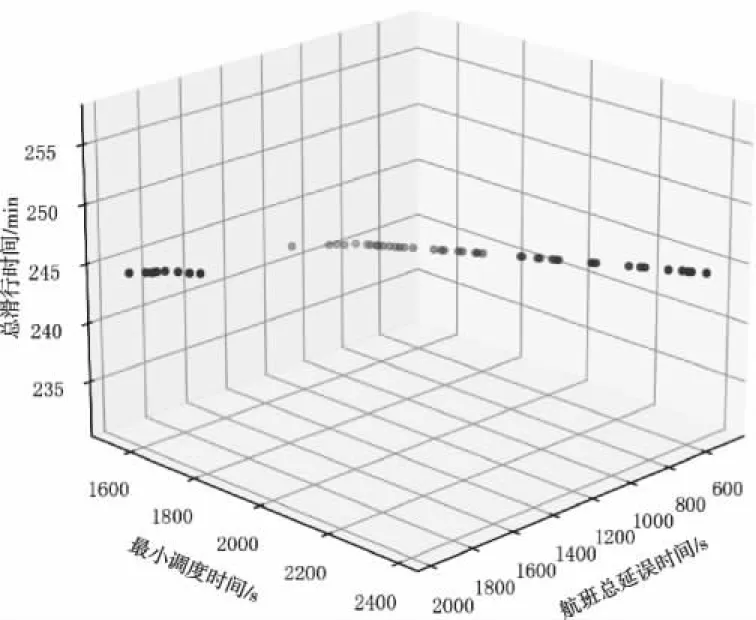
图1 种群进化得到的部分Pareto最优解

图2为模型在进化过程中不同评价指标数值变化趋势,可以看出随着种群的不断进化,GD和IGD的数值逐渐降低并趋向于一致,HV值逐渐增大并最终趋于稳定。

图2 种群进化过程指标值变化趋势

选取其中一个pareto最优解进行分析,如图3所示,可以得到先到先服务(First Come First Serve, FCFS)策略下的航班总延误为4049.16秒,优化策略下的航班总延误为1201.4秒,相比降低70.33%,FCFS策略下的跑道调度时间为2920.20秒,优化策略下的跑道调度时间为1730秒,相比降低40.76%,FCFS策略下的航班总平均滑行时间为15033秒,而优化策略下的时间为14655秒,相比降低了3%左右。因此优化模型在降低航班延误以及提升跑道容量方面效果显著。

图3 不同策略下三个目标函数值

如果离场航班优化起飞次序与计划起飞次序偏差较大,则会增加管制员工作负荷,同时降低旅客满意度。如图4所示,基于优化模型结果的航班起飞次序与FCFS策略安排的起飞次序变化均满足MPS约束,因此符合实际管制运行的需要。

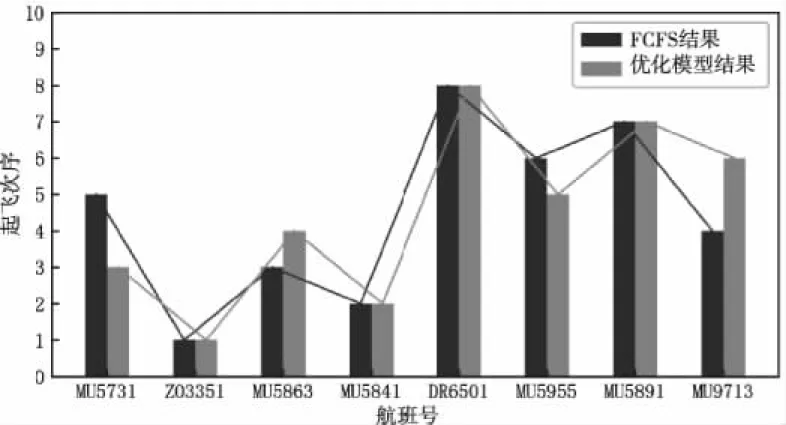
图4 调度时间段内两种策略航班的起飞次序

5 结论

航班离港是空中交通运行的重要组成部分,为了提升场面运行效率,从时空角度出发,考虑了尾流间隔、时间窗等约束,在已有文献目标函数的基础上提出了以最小化跑道分配的多目标离场航班调度模型,并采用多目标遗传算法进行求解最优解,以实例数据进行仿真验证,结果表明了相比FCFS策略,优化后的航班延误以及场面运行时间明显得到降低,可以用于实际管制中的辅助决策。