叶顶间隙对叶轮内部流动与变形影响的流固耦合分析*

贺诗榕 董志强 刘 通

（太原科技大学机械工程学院 山西太原 030024）

离心空压机是输送和压缩气体的核心装备， 近年来广泛应用于航天航海以及汽车等领域［1］。 得益于电机技术、 密封技术与空气轴承等关键技术的发展， 空压机的工作压比大幅度提高， 叶轮能承载的转速达到了万转以上［2］。 半开式叶轮由于减少了轮罩的束缚，可以承载更高的许用圆周速度， 适合高转速的工况，凭借这一优势广泛应用于转速高的工况环境［3］。 但没有轮罩， 叶片与机壳间势必存在一定的间隙， 工作时不可避免地出现气体泄漏、 潜流损失与气流分离等现象， 影响整个叶轮内部的气体流动情况， 降低了压缩机的效率。 另一方面， 空压机在工作时处于高温高压高转速的环境中， 会产生振动与结构热变形， 若叶顶间隙过小， 很有可能使叶片与机壳发生碰撞， 影响空压机的安全性。 因此， 在叶轮设计时确定合适的叶顶间隙尤为重要。

关于叶轮叶片数影响的研究方面， 靳亚峰等［4］用NUMECA 软件分析了叶轮叶片数对离心压缩机机组性能的影响， 发现叶片数过多会导致摩擦损失过大，机组效率下降， 叶片数过少， 叶片载荷分布增加， 二次流损失严重； 席光等人［5］从叶片厚度分布入手， 发现对等厚叶片沿展向和流向进行合理地削薄， 能显著提升叶轮在大流量工况下的性能； 王艺达等［6］从叶轮叶片数、 进口倾角和子午流道型线控制点和叶片安装角分布控制点等关键构型参数出发， 用数值计算方法对离心压缩机的叶轮进行优化。 关于叶顶间隙影响的研究方面， 姬田园等［7］对叶片前后缘的叶顶间隙进行尺寸波动干扰， 发现叶顶间隙主要对80%叶高以上部分的流场产生影响； 叶顶间隙存在偏差会产生泄漏流， 影响叶片的工作裕度； 刘玉文等［8］通过流场测量实验和空化观测实验， 发现间隙流动中主要有2 种稳定涡， 分别是泄漏涡和分离涡， 它们是引起叶顶间隙流动空化的主要因素。 针对叶轮机械在旋转时发生的振动与变形问题， 方绍寒等［9］以离心风机叶轮为研究对象， 采用k-ε湍流模型与振动力学理论， 对叶轮结构及其流场进行分析， 得到叶轮的变形情况； 高亚飞［10］基于流固耦合理论， 运用数值模拟方法对离心泵叶轮进行仿真计算， 得到了应力应变云图。

目前学者们针对压气机工作稳定裕度范围小、 效率低等问题已进行了深入研究， 但针对叶轮叶顶间隙大小对空压机可靠性的影响研究较少。 在实际工程应用中， 需要保证叶轮运行稳定， 避免产生安全隐患。所以叶轮的可靠性分析必不可少， 特别是在进行叶轮的设计及优化时， 效率及稳定性都要考虑在内。 董振等人［11］以轴向迷宫密封为例， 基于流固耦合理论，对迷宫密封的流场分布与结构进行数值分析与优化。传统的可靠性分析只考虑叶轮的离心载荷， 这与真实工况环境相差甚远。 张衎和梁尚明［12］采用CFD 技术对叶轮内的流道进行数值模拟， 研究表明工作压力越高， 流体载荷越大。 李彦启等［13］以镶嵌式机械密封为研究对象， 通过对结构受力分析和热传导方程， 建立热力耦合仿真模型并进行求解， 发现热应力对端面造成的变形量大于结构应力。

考虑到叶轮叶顶间隙的大小对空压机可靠性的影响研究较少， 且在进行数值计算时容易忽略气动载荷与热载荷对叶轮的影响， 本文作者建立空压机叶轮的三维模型， 在不同叶顶间隙下进行流场的数值模拟计算； 基于流固耦合理论建立热流固模型， 进行叶轮的动力学分析； 综合探究离心力、 气动力和热应力3 种载荷对叶片叶顶处应力和变形的影响， 为叶片的结构优化提供理论参考。

1 计算方法

1.1 理论模型

1.1.1 流动方程

采用流体运动的控制方程， 即雷诺方程， 来描述流体的运动规律［14］。 质量方程、 动量方程、 能量方程分别为

式中：ρ为流体密度， kg／m3；t为时间， s；U为速度矢量；u、v、w分别为速度矢量在x、y、z方向的分量；μ为动力黏度， Pa·s；Su、Sv、Sw为动量守恒方程的广义源项；cp为流体比定压热容， J／（kg·K）；T为流体的温度， K；k1为流体的传热系数，W／（m·K）；ST为黏性耗散项。

1.1.2 湍流模型

由于CFX 具有丰富的物理模型， 文中采用CFX进行叶轮的流场模拟实验， 用叶轮流体域的雷诺数来确定其流动情况。 雷诺数定义为

式中：ρ为流体密度， kg／m3；μ为流体动力黏度， MPa·s；v为速度， m／s；L为流体域的长度， m。

将叶轮物理模型几何参数代入式（6） 计算可得，Re＝1.293×30×0.024 4／（18.16×10-6）＝51 189≫2 300， 由此可确定流体的运动状态为湍流。

由于k-ε湍流模型具有很好的预测能力， 又易于收敛， 适合绝大多数的工程湍流模型［15］， 所以文中的流动模型选用CFX 默认的k-ε模型。 其中，k为湍动能， m2／s2；ε为湍动能耗散， m2／s3。

1.1.3 结构力学方程

由经典力学可知， 物体动力学通用方程为

式中：M是质量矩阵；C是阻尼矩阵；K是刚度矩阵；是加速度矢量；是速度矢量；x是位移矢量；F（t）是力矢量。

1.2 物理模型

利用Cfturbo 软件对离心空压机叶轮进行三维建模， 叶片几何参数如表1 所示， 叶轮实体模型如图1所示。

图1 叶轮实体模型Fig.1 Solid model of impeller

表1 叶轮几何参数Table 1 Geometrical parameters of impeller

叶顶间隙指叶片的顶部与机壳之间的距离， 靠近叶片前缘的间隙称为径向叶顶间隙， 靠近后缘的间隙称为轴向叶顶间隙。 文中设径向与轴向的间隙值相同， 即S径向＝S轴向＝S， 离心空压机叶轮横截面如图2所示。

图2 叶轮横截面Fig.2 Impeller cross section

1.3 流固耦合

采用分离求解（不同的求解器计算各自的物理变量， 共同变量采用异步传递的方式进行更新） 的计算方式， 以及单向的数据传递方式， 将流体求解器（CFX） 计算出的压力、 温度数据作为载荷传递到固体上， 由固体求解器（Mechanical） 计算出位移应力等信息。 对离心式压气机叶轮进行单向流固耦合求解分析如图3 所示。

图3 单向流固耦合流程Fig.3 Flow of one way fluid-structure coupling

1.3.1 固体控制方程

由牛顿第二定律得：

温差引起的热变形为

式中：ρs为固体密度， kg／m3；as为固体域当地加速度矢量；σs为柯西应力张量；fs为体积力矢量；αT为热膨胀系数，℃-1。

1.3.2 流固耦合方程

由于流固耦合数值计算时流体模型和结构模型是分开建立的， 所以耦合面上须满足以下条件［16］：

式中：τ为应力， Pa；d为位移， m；Φ为热流量， W； 下标f 表示流体， s 表示固体。

1.4 网格无关验证及边界设置

1.4.1 网格划分与无关性验证

由于叶轮几何模型复杂， 曲率变化剧烈， 为了获得较高的网格质量， 文中采用ICEM 对叶轮的流体区域进行非结构化网格划分。 选用四面体划分网格， 整体网格单元尺寸因子设为3， 叶片、 轮缘以及轮毂处的网格大小设为1 mm。 由于文中主要研究叶顶处的流动情况， 故将叶片顶部的网格进行加密处理， 设置单元大小为0.1 mm。 考虑到叶顶间隙较小， 叶轮出口处的网格也进行加密， 设置单元大小为0.1 mm。图4 所示为叶轮流体域网格分布。

图4 离心叶轮流体域网格分布Fig.4 Grid distribution of fluid area of centrifugal impeller

为保证结果的准确性， 以S＝0.5 mm 的叶轮为例， 进行网格无关性分析。 如图5 所示， 当网格数量达到100 万后， 网格数对叶轮的等熵效率和多变效率影响较小。 在保证计算精度的基础上， 考虑到节约计算资源， 最终选取网格单元数为966 759， 总节点数为17 338。

图5 网格无关性验证Fig.5 Grid independence verification

1.4.2 边界条件

工质选用可压缩性理想空气， 湍流模型为k-ε模型， 参考压力为0.1 MPa， 壁面与叶轮表面采用绝热无滑移条件， 内部传热设置为Total Energy。 进口总压为一个标准大气压 （0.1 MPa）， 进口温度为288.15 K， 出口压力为0.3 MPa。 求解设置采用物理时间步长， 迭代步数为200。 叶片选用高强度的钛合金材料， 密度为4 620 kg／m3， 屈服应力为930 MPa。

2 气动力学分析

2.1 气动性能分析

计算中保持叶轮的基本形状不变， 仅改变叶顶间隙的大小。 设定叶轮的旋转速度为120 000 r／min， 分别选取S＝0.1、 0.3、 0.5、 0.7、 0.9、 1.1 mm 进行计算， 得到不同叶顶间隙下的叶轮压比与效率， 如图6 所示。

图6 叶轮气动性能Fig.6 Aerodynamic performance of impeller

从图6 中可以看出， 叶顶间隙在由0.1 mm 增大到1.1 mm 的过程中， 叶轮的压比呈现上升态势， 由3.006 增长到3.27， 1.1 mm 时的压比值比设计压比增加了9%， 并且还有向上增长的趋势； 叶轮的等熵效率呈逐步下降的趋势， 由92.42%降低到81.25%。间隙从0.1 mm 增加到0.7 mm 的过程中， 效率下降幅度比较明显， 而从0.7 mm 增大到1.1 mm 时， 叶轮的效率下降曲线较之前相对平缓， 说明效率下降程度与叶顶间隙大小不是呈线性的变化关系。 上述结果表明叶顶间隙的大小对空压机效率的影响非常大， 随着间隙值的增大， 气动性能对其不再敏感， 即S存在最优解。

2.2 流动特性分析

2.2.1 流线分析

设计工况下离心叶轮通道内流线如图7 所示。 可见， 紊流首先出现在叶轮的进口处， 随着间隙值的增大， 叶轮入口处的气流流动越发不均匀， 致使入口处流场紊乱， 这部分气流进入主流道内， 造成主流流场失稳。 这对压气机的效率以及运行时的可靠性都产生了一定的威胁。S＝0.1 mm 时的流动最为平稳， 速度分布均匀。 与之相比，S＝0.3 mm 的流场图入口处的流速相对均匀， 但是原本靠近叶片前缘的高速气流变为紊乱的低速气流， 这不利于整机的流动。 间隙越大， 入口紊流的区域也随之变大。S＝1.1 mm 时， 入口叶片前缘处出现了较多的涡流， 涡流区占据了叶轮入口流体区域的50%。

图7 叶轮整体流线Fig.7 Integral streamline of impeller： （a） S＝0.1 mm； （b） S＝0.3 mm； （c） S＝0.5 mm；（d） S＝0.7 mm； （e） S＝0.9 mm； （f） S＝1.1 mm

由于间隙的存在， 随着叶片的旋转方向， 在叶顶处产生泄漏流， 该气流分为两部分。 一部分低速气流从叶片前缘至中部的压力面透过叶顶进入叶片吸力面的前半部分， 形成涡流， 在吸力面一侧形成很明显的低速区。 随着间隙值增大， 叶片顶端附近的泄漏流动影响范围扩大， 即低速区越大。 这是因为间隙越大，泄漏流的流量越大造成的。 另一部分从叶片中后缘透过叶顶进入相邻流道内， 与其主流线发生掺混。 随着间隙增大， 泄漏流与主流的掺混更为剧烈， 范围也越大。 这两部分的泄漏流在叶轮主流道内造成了气流堵塞， 产生了较大的流动损失， 但在一定程度上提高了主流区气流的压力， 提高了压比。 当S＝0.1 mm 时，叶片顶部几乎无泄漏流。 叶轮内流线平稳， 且都为高速气流， 流动状态良好， 这也是该叶轮效率最高的原因。 间隙值增大到1.1 mm 时， 泄漏量最大， 这两部分的泄漏流都通过叶顶间隙流入相邻流道， 与主流掺混， 混流区域占据总流道的1／2 左右。

2.2.2 叶片载荷分析

叶片吸力面与压力面的压差为叶片的载荷， 它决定了叶轮的做功能力。 图8 所示为不同叶高的叶片静压分布。

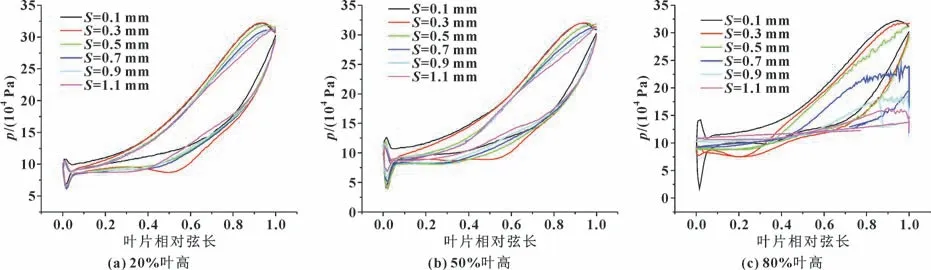
图8 不同叶高处叶片静压分布Fig.8 Static pressure distribution of blade at different leaf heights： （a） 20% leaf height； （b） 50% leaf height； （c） 80% leaf height

由图8 （a） 可知， 不同叶顶间隙时的叶片载荷，在20%叶高处几乎相同， 说明叶顶间隙对叶高20%以下的气流影响不大。 由图8 （b） 可知， 在50%叶高处，S＝0.3 mm 时， 叶片前半部分（0.0 ～0.25 弦长） 的叶片载荷比S＝0.1 mm 时的叶片载荷小很多，这是因为间隙0.3 mm， 叶轮入口处发生紊流， 而这部分气流随叶片进入主流道， 扰乱了叶片压力面上的流动， 使得载荷降低。 在0.5 弦长之后， 叶片的载荷缓慢上升， 叶轮整体的做功能力略微减弱。 由图8 （c）可知， 80%叶高处的载荷情况与前者相比能更加直观准确地反映出叶顶间隙的大小对叶片做功能力的影响， 随着叶顶间隙的增大， 叶片压力面和吸力面的压差整体都在减小， 叶轮的做功能力明显下降。 特别是S＝1.1 mm 时， 叶片上出现负载荷， 不利于叶轮的做功。

2.2.3 速度分析

80%叶高处不同间隙的叶片附近绝对速度的分布云图如图9 所示。 当间隙为0.1 mm 时， 在叶片吸力面后缘发现小范围低速区， 这个现象一部分是由于附面层分离所导致的， 另一部分是间隙泄漏流与主流区掺混在流道前中部形成的低速涡流。 随着间隙的增大， 低速区面积范围扩大， 通道内的有效通流面积逐渐减小。 以上分析表明， 间隙越大， 泄漏量越多， 径向间隙过大造成的低速气流积聚在吸力面， 增大了能量损失， 降低了叶轮效率， 所以减小径向叶顶间隙可以有效减少流道内涡流， 降低流动损失。

图9 80%叶高处叶片绝对速度分布Fig.9 Blade absolute velocity distribution on 80% blade height

2.2.4 马赫数分析

图10 所示为叶轮子午面马赫数的分布情况。 可知， 所有叶轮的马赫数都不超过1， 所以在叶轮中不会产生激波， 使得边界层分离而影响空压机的可靠性。 当S＝0.1 mm 时， 流体运动相对平缓， 马赫数分布均匀。 叶片前缘处马赫数较大， 是因为气流在靠近叶片前缘时出现膨胀加速。 在轮缘中部出现由于急转弯， 流动扩压度突然增大导致的气流分离从而产生的低速区， 而在轮毂处则出现由于附面层分离产生的低速角区。 随着间隙值的增加， 角区逐渐消失。 说明泄漏流在一定程度上可以有效带动轮毂处的低速气流运行， 缓解此处的流动情况。S＝0.3 mm 时， 由于泄漏流的影响， 轮缘侧流动分离区域显著扩大， 并且随着间隙的增大， 分离区也随之增大，S＝1.1 mm 时的分离区约占整个子午面流道的35%。 这表明叶顶处的泄漏流由叶片压力面通过叶顶间隙向吸力面扩散， 且间隙越大， 扩散程度越大。

图10 子午面马赫数分布Fig.10 Mach number distribution on meridianal plane

3 结构力学分析

3.1 载荷对叶片形变以及应力大小的影响

为研究离心力、 气动力以及热载荷对叶片形变的影响程度， 取S＝0.5 mm 时的叶片进行仿真， 得到如表2 所示的数据。

表2 叶片的形变与应力Table 2 Deformation and stress of blade

由表2 可知， 气动力与热载荷造成的形变分别约占叶片总形变量的5%和10%， 所以在数值计算中，求解结构的变形以及应力时这二者的大小不可忽略，也体现了文中计算叶片变形时利用流固耦合方法的必要性。 对比第1 组和第4 组数据， 发现离心力和气动力的载荷导致的叶片形变量还没有单个离心力造成的形变大， 是因为气流运动方向与叶轮旋转方向相反，气动力导致的形变方向与离心力相反。 由于叶片的最大变形量为0.187 2 mm， 远小于叶片的几何尺寸，并且气动力和热载荷产生的等效应力很小， 分别为23.6 和30.7 MPa， 说明双向耦合结果与单向耦合结果相差不大， 这也是文中选用单向流固耦合的原因。叶片的形变所引起的流场变化对模拟计算的结果影响较小， 可以忽略。 考虑到单向耦合问题不涉及流体域的变化， 所以文中没有采用动网格。

3.2 间隙对叶片形变以及应力大小的影响

图11、 12 所示为叶轮叶片在3 种载荷共同作用下的总变形以及等效应力云图。 由图11 可知， 不同叶顶间隙的叶片变形趋势一致。 较大变形主要集中在叶片前缘叶顶处， 说明叶片的高度对叶片的形变位置没有影响。 由于轮盘的固定支撑作用， 变形程度沿着周向位置向叶根部分逐渐降低。S＝0.1 mm 时的最大变形量达到了0.195 68 mm， 占前缘总叶高的1.25%， 超过了设定的叶顶间隙值， 叶轮运行时会与机壳发生碰撞， 所以叶轮在设计时要充分考虑叶顶间隙的大小。

图11 叶片的位移分布Fig.11 The deformation distribution of blade： （a） S＝0.1 mm； （b） S＝0.3 mm； （c） S＝0.5 mm；（d） S＝0.7 mm； （e） S＝0.9 mm； （f） S＝1.1 mm； （g） new blade

从图12 可看到， 叶片前缘叶顶处的应力最小，叶高30%～40%处的应力最大， 出现明显的应力集中部位。 钛合金的屈服极限强度为930 MPa， 根据强度屈服理论：

图12 叶片的等效应力分布Fig.12 Equivalent stress distribution of blade： （a） S＝0.1 mm； （b） S＝0.3 mm； （c） S＝0.5 mm；（d） S＝0.7 mm； （e） S＝0.9 mm； （f） S＝1.1 mm； （g） new blade

式中：σmax为最大应力， MPa； ［σs］ 为屈服极限，n为安全系数， 一般取2～5。

所以叶片上的最大应力小于等于465 MPa 较为安全可靠。

图12 中S＝0.1 mm 与S＝0.3 mm 时， 叶片的最大应力分别为481.73 和492.7 MPa， 都大于465 MPa的安全值， 说明该类叶轮设计不合理。 由此可以在应力集中处对叶片表面进行强化处理或适当地增加叶片的厚度。 为了不增加叶片制造成本， 文中将在应力集中处适当地增大和减小叶片的厚度， 以达到对叶轮优化设计的目的。

为了分析流固耦合作用下叶片顶部的变形特征，提取不同叶高叶片顶部的变形与应力信息绘制成曲线图， 如图13、 14 所示。 由图13 可以看出， 叶片顶部变形最大的区域在弦长0.35 左右， 叶片吸力面与压力面的变形趋势相同， 发生较大变形的位置相同， 但最大变形量不同， 吸力面比压力面变形大3.7%左右； 随着间隙值的增大， 顶部的变形随之减少。 由图14 可以看出， 在叶片顶部， 前缘的应力最小， 其压力面与吸力面的等效应力分布存在差异， 吸力面应力最大在弦长0.75 处， 压力面应力最大值在弦长0.55处； 随着间隙值的增大， 顶部的应力值整体逐渐降低。 以上分析表明， 在设计叶片时应适当降低叶片0.3～0.4 弦长处的叶高， 削薄叶片前缘的厚度， 增加0.55～0.75 弦长处的叶高， 增加30%～40%叶高处的叶片厚度。

图13 叶片顶部变形分布曲线Fig.13 The deformation distribution curves on blade tip

图14 叶片顶部等效应力分布曲线Fig.14 Equivalent stress distribution curves on blade tip

4 线型优化

在保证叶轮气动性能的基础上， 从叶轮的安全性出发， 结合上文结构力学分析得到的结论， 对原始叶片进行模型的改进： （1） 将叶片径向间隙值设为0.3 mm， 轴向间隙值设为0.2 mm； （2） 将叶片轮毂侧前后缘的厚度设为0.8 mm， 轮缘侧前后缘厚度分别设为0.5、 0.7 mm； （3） 具体厚度分布情况由具体点用贝塞尔曲线连接而成， 如图15 所示。 将改进后的叶片重新建模， 再进行仿真分析。

图15 叶片厚度分布曲线Fig.15 Blade thickness distribution curves

数值计算得到新叶片的等熵效率为90.416%， 压比为3.08， 达到了工程要求。 由图11—14 可以看出，新叶片上的最大变形为0.189 16 mm， 且主要分布在前缘， 在给定的间隙值0.3 mm 之内， 运行时不会与机壳发生碰撞， 保证了机器的安全性； 叶片上的最大应力为382.25 MPa， 与S＝0.3 mm 叶片上的应力相比， 降低了22.42%， 大大提高了机器的可靠性。

5 结论

（1） 叶顶间隙的大小对空压机效率影响非常大，径向间隙会造成叶轮进口处的气流紊乱， 也会产生叶片前缘处的泄漏流， 二者共同作用使主流流场失稳；轴向间隙产生叶片后缘处的泄漏流， 与相邻流道的主流线发生掺混， 进一步增加了流动损失。

（2） 气动力与热载荷造成的形变分别约占叶片总形变量的5%和10%， 所以求解结构变形以及应力时二者不可忽略； 气动力造成的形变方向与离心力相反。

（3） 不同叶高的叶片变形趋势基本一致， 较大变形区主要集中在叶片前缘叶顶弦长0.35 处， 其变形量的大小随叶高减小而减小， 变形程度沿着周向位置向叶根逐渐降低； 叶片叶高30%～40%处的应力最大， 出现应力集中。 叶顶前缘处的应力最小， 吸力面与压力面的应力最大值分别在弦长0.75 和0.55 处，且顶部的应力值随间隙的增大逐渐降低。

（4） 通过对叶片顶部的流场和结构力学分析，确定了最佳间隙值， 给出了叶片的线型优化方案。 优化模型的结果显示叶轮气动性能达到了工程要求， 叶片变形量在允许范围内， 整体应力值得到显著降低，为空压机叶片的工业设计提供了参考。