多姿多彩的非线性回归分析问题

■广东省兴宁市第一中学 蓝云波

■广东省梅州市教育局教师发展中心 陈启南

回归直线方程是高考中的高频考点,对大部分同学而言,掌握得比较好。但是随着高考命题越来越注重考生的应变能力,对应用已学知识求解或探索创新问题提出了越来越高的要求。非线性回归分析问题正是基于此而命制的一类创新问题。所谓非线性回归分析问题,指的是当两个变量具有相关关系,但又不呈线性相关关系时,可依据样本点的分布选择合适的曲线方程来模拟,并设法求得其回归方程的一类问题。常见的非线性回归分析问题有二次函数型、根式型、倒数型、指数型与对数型。通过研究分析,我们发现建立非线性经验回归模型的基本步骤如下:

1.确定研究对象,明确哪个是解释变量,哪个是响应变量;

2.由经验确定非线性经验回归方程的模型;

3.通过变换(换元,取对数,指数式、对数式互化等),将非线性经验回归模型转化为线性经验回归模型;

4.按照公式计算经验回归方程中的参数,得到经验回归方程,需要特别注意的是,使用线性回归方程的公式,要注意代入变换后的变量;

5.消去新元,得到非线性经验回归方程。

下面将对这五类问题逐一进行阐述,希望能为同学们彻底解决非线性回归分析问题提供一些借鉴,并帮助同学们通过学习与研究,提高自己的数学素养与能力水平。

一、二次函数型回归方程

例1(山东省潍坊市2022 届高三核心素养测评)2021年11月4日,第四届中国国际进口博览会在上海开幕,共计2 900 多家参展商参展,420 多项新产品、新技术、新服务在本届进博会上亮相。某投资公司现从中选出20 种新产品进行投资。为给下一年度投资提供决策依据,需了解年研发经费对年销售额的影响,该公司甲、乙两部门分别从这20种新产品中随机地选取10 种产品,每种产品被甲、乙两部门是否选中相互独立。

(1)求20 种新产品中产品A被甲部门或乙部门选中的概率。

(2)甲部门对选取的10种产品的年研发经费xi(单位:万元)和年销售额yi(i=1,2,…,10)(单位:十万元)数据作了初步处理,得到散点图(图1)及一些统计量的值。根据散点图现拟定y关于x的回归方程为=(x-3)2+,求的值(结果精确到0.1)。

表1

图1

(3)甲、乙两部门同时选中了新产品A,现用掷骰子的方式确定投资金额。若每次掷骰子点数大于2,则甲部门增加投资1万元,乙部门不增加投资;若点数小于3,则乙部门增加投资2 万元,甲部门不增加投资。求两部门投资资金总和恰好为100万元的概率。

二、根式型回归方程

例2(2015年高考全国Ⅰ卷)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到散点图(图2)及一些统计量的值(表2)。

表2

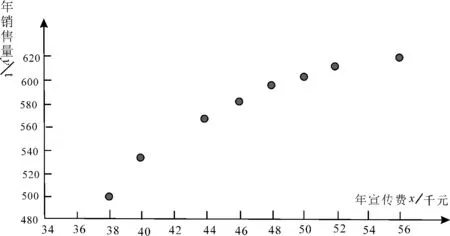
图2

(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程。

(3)已知这种产品的年利润z与x、y的关系为z=0.2y-x。根据(2)的结果回答下列问题:

(i)年宣传费x=49时,年销售量及年利润的预报值是多少?

(ii)当年宣传费x为何值时,年利润的预报值最大?

三、倒数型回归方程

例 3快递业的迅速发展导致行业内竞争日趋激烈。某快递网点需了解一天中收发一件快递的平均成本y(单位:元)与当天揽收的快递件数即揽件量x(单位:千件)之间的关系,对该网点近7天的每日揽件量xi(单位:千件)与当日收发一件快递的平均成本yi(单位:元)(i=1,2,3,4,5,6,7)的数据进行了初步处理,得到散点图(图3)及一些统计量的值(表3)。

表3

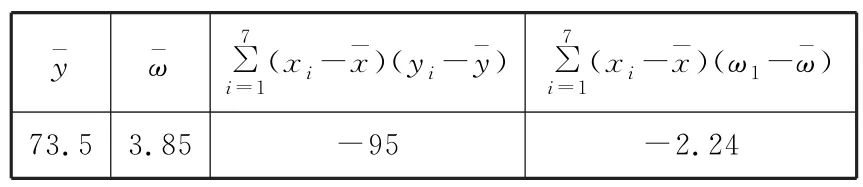
表4

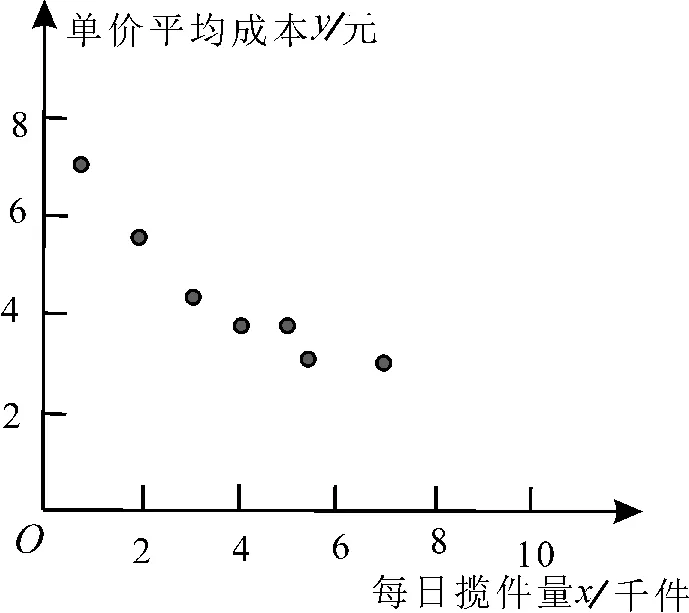
图3

(1)根据散点图判断y=ax+b与y=哪一个更适宜作为y关于x的经验回归方程类型,并根据判断结果及表中数据求出y关于x的经验回归方程。

(2)已知该网点每天的揽件量x(单位:千件)与单件快递的平均价格t(单位:元)之间的关系是(5.75≤t≤14.5),收发一件快递的利润等于单件的平均价格减去平均成本。根据(1)中建立的经验回归方程解决以下问题:

①预测该网点某天揽件量为2千件时可获得的总利润;

②单件快递的平均价格t为何值时,该网点一天内收发快递所获利润的预报值最大?

所以当x=4时,zmax=27,此时t=10.75。故单件快递的平均价格t=10.75元时,该网点一天内收发快递所获利润的预报值最大。

点评:本题形式上与上两道例题不一样,但都可以直接通过换元,转化为线性回归分析问题。通过熟悉相关技巧,就能应对自如。第二问得到的收发x千件快递获利z是一个三次函数,故可以通过导数的相关知识实现问题的求解。

四、指数型回归方程

例4(福建省泉州市2023 届高三质量监测)中国茶文化博大精深,饮茶深受大众喜爱。茶水的口感与茶叶类型和水的温度有关。某数学建模小组为了获得茶水温度y(℃)关于时间x(min)的回归方程模型,通过实验收集在25℃室温,用同一温度的水冲泡的条件下,茶水温度随时间变化的数据,并对数据进行初步处理得到如图4所示散点图。

图4

(1)根据散点图判断,①y=a+bx与②y=d·cx+25哪一个更适宜作为该茶水温度y关于时间x的回归方程类型。(给出判断即可,不必说明理由)

(2)根据(1)的判断结果及表中数据,建立该茶水温度y关于时间x的回归方程。

(3)已知该茶水温度降至60℃口感最佳。根据(2)中的回归方程,求在相同条件下冲泡的茶水大约需要放置多长时间才能达到最佳饮用口感。

(2)参考数据:e-0.08≈0.92,e4.09≈60,ln 7≈1.9,ln 3≈1.1,ln 2≈0.7。

解析:(1)根据散点图判断,其变化趋势不是线性的,而是曲线的,因此,选②y=d·cx+25更适宜作为本题的回归方程。

所以回归方程为y=d·cx+25=e4.09·e-0.08x+25=e4.09-0.08x+25。

(3)当y=60 时,代入回归方程y=e4.09-0.08x+25得60=e4.09-0.08x+25,化简得35=e4.09-0.08x,即4.09-0.08x=ln 35。

又e-0.08≈0.92,e4.09≈60,ln 7≈1.9,ln 3≈1.1,ln 2≈0.7,所以4.09-0.08x=ln 35化为ln 60-0.08x=ln 35,即0.08x=ln 60-ln 35==ln 12-ln 7=(2ln 2+ln 3)-ln 7≈2×0.7+1.1-1.9=0.6,x≈=7.5。故大约需要放置7.5 min 才能达到最佳饮用口感。

点评:本题直接通过换元,难以实现问题的求解,但在通过移项与取对数之后,再利用换元即可转化为线性回归分析问题,相比前几题,难度更大。对于形如y=d·cx+k的回归模型,都可以通过这样的方式进行化归。实际上,本题中给出的信息wi=ln(yi-25)即是解题的提示,希望同学们能用心体会,以达到触类旁通的效果。

五、对数型回归方程

例5(湖北省武汉市2021届高三五月调考)某市号召市民接种疫苗,提出全民“应种尽种”的口号,疫苗成了重要的防疫物资。某疫苗生产厂不断加大投入,高速生产,现对其某月内连续9天的日生产量yi(单位:十万支,i=1,2,…,9)数据作了初步统计,得到如图5 所示的散点图及一些统计量的数值(表5)。

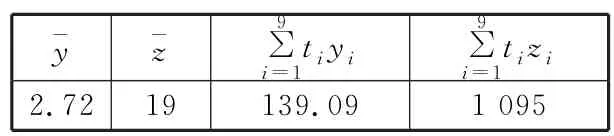
表5

图5

点评:本题第一问考查了利用组合知识求解古典概型的问题,难度一般。第二问可以通过指数式对数式互化后,再利用换元思想化归为线性回归分析问题。

通过以上的分析,我们可以发现,解决非线性回归分析问题,关键在于通过恰当的变换,转化为线性回归分析问题。而换元、取对数、指数式对数式互化是变换的常见技巧,值得大家用心体会,从而做到心中有数、触类旁通。