层级化 多层次 立体化——陈淑娟老师《包装的学问》教学片断赏析

文|王明滨

随着《义务教育数学课程标准（2022年版）》的颁布，“综合与实践”领域迎来了内容变化最大和教学挑战最强的一次转变。不但课时增加了，相应的内容也得到了充实。“包装的学问”作为北师大版“综合与实践”领域的内容，是在学生学习了长方体表面积和体积之后的一次“综合应用”，是落实核心素养的一次实践性、探索性和研究性的学习。笔者有幸学习了厦门市海沧区教师进修学校陈淑娟老师执教的课例《包装的学问》。作为“说理”课堂的引领者和践行者之一，陈老师在课堂上展示出层级化的课程思维，借助《学习单》让学生思维可视化的教学手段和立体化的共通能力，培养学生的核心素养，值得每一位教师跟进学习。

片断一：层级化的课程思维

师：今天要研究的问题是？

生：包装中的学问。

师：想一想，在生活中的包装可能遇到什么样的数学问题？

生：一个东西的外表要用到多少包装纸？有时候包装要镶边就要计算棱长总和。

生：这个包装能容纳多少东西？

生：包装有时候是很多东西放在一起，可能要求重叠的两个面的面积。

生：还可能让我们求包装需要的彩带有多长。

生：怎样包装更节省纸？

师：那今天我们来研究什么问题呢？

出示任务：下图是一盒馅饼的尺寸，商家要把十盒这样的馅饼包装成一箱进行销售，请帮他想想，怎样设计纸箱才最节约纸皮？（纸皮的厚度和衔接处忽略不计）

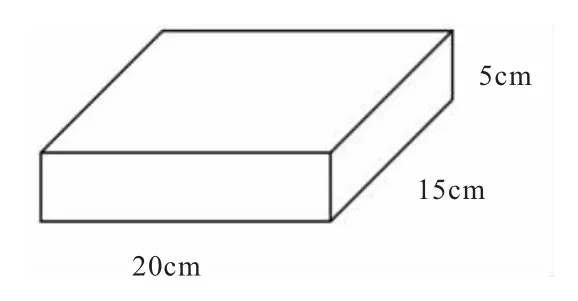
【赏析：“我们要建立从培养目标到课程标准再到教学目标的层级化的‘树人’目标体系。课程思维本来就需要一致性地思考在目标统领下的教学、学习、评价的问题，所有单一或点状的思考都不是课程思维，而是人们常说的教学思维。”从“在生活中的包装可能遇到什么样的数学问题”说开，所有的问题都来源于学生已有的数学现实。在学生所有单一或点状的思考中，逐渐构筑出一个庞大的课程体系，涉及到长方体和正方体的棱长总和、表面积、容积和体积等数学问题，还有实际包装中可能遇到的各种问题。在这样开放的问题中，体现了问题设置的“低门槛”和“大空间”的特点，每位学生都能结合自身的生活经验和学习经验提出想研究的数学问题。避免一入课就“计算两盒糖果包成一包的表面积”的做法。在这段看似轻松随意的谈话中，可以看出一个执教者的课程思维，站在更宏观的角度来思考包装中可能涉及的数学问题。这就要求每一位教师都要像专家一样来思考我们的教学，从以往的教学思维转向课程思维，做到心中既有核心素养目标导向，又有课程标准的教学准绳，唯有这样才有教学目标的落实。】

片断二：多层次的学习路径

师：怎样才能最节约纸皮呢？

生1：我们得出的最佳方案是长30cm、宽20cm、高25cm（如下图），先把每个人的方案都展示出来，再看哪个表面积是比较节约的，发现长、宽、高越接近的，表面积就会越小一些。

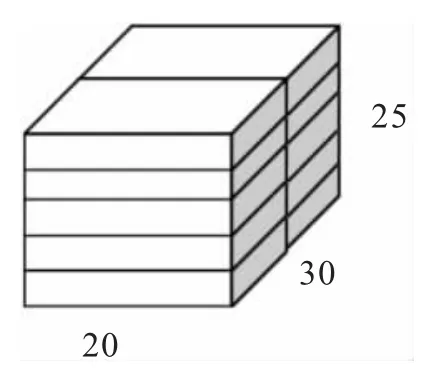
方案一的表面积：（20×30+20×25+30×25）×2=（600+500+750）×2=3700（cm2）

生2：为什么不把十个叠在一起呢？

生1：把十个叠在一起（出示方案二），发现高是50cm，50cm 与另外两条棱的数据差太多了，所以淘汰掉了。

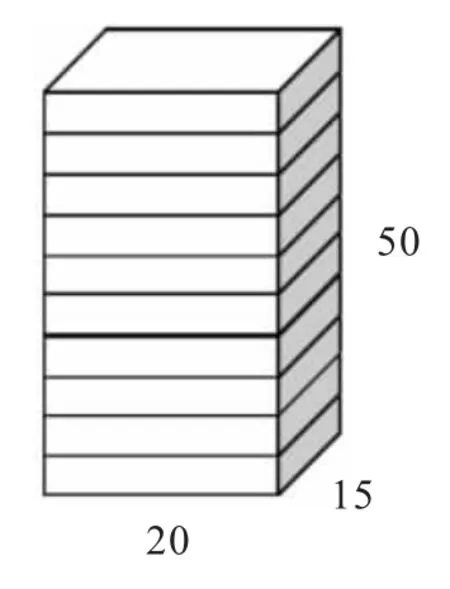
方案二的表面积：（20×50+15×50+20×15）×2=（1000+750+300）×2=4100（cm2）

师：在讨论中有什么发现吗？

生：我们发现看似越不可能的方案可能会更好一些。

师：有比较有趣的方案吗？

生3：有趣的方案就是这个交叉的（出示方案三），但并不是最节约的。方案一是最节约的。

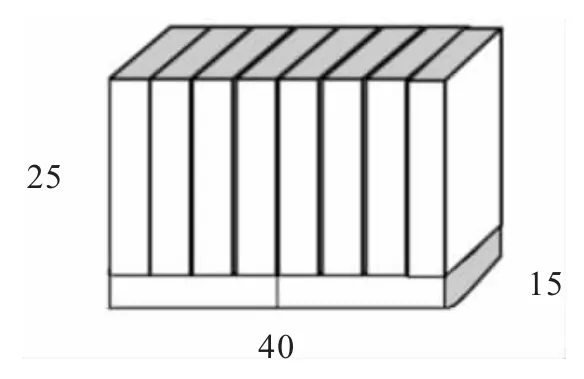
方案三的表面积：（40×25+15×25+40×15）×2=（1000+375+600）×2=3950（cm2）

师：还有愿意分享的吗？

生4：我们讨论出来的方法也是一样的，本来打算十个叠在一起，但不是最节省的。虽然15×20一开始是最大的面，但是把五个叠在一起后，最大的面就变成20×25，这时就产生了新的大面，所以把两个20×25 的面叠在一起，就节省了两个新的最大的面。

生5：我们还找到了一个比较有意思的方案（出示方案四）。先把它分成三份，竖着放4 个，再往上叠一层，最后横着放2 个，得出长20cm、宽15cm、高50cm。虽然不是最少的，但刚好也能摆成一个长方体，所以比较有趣。

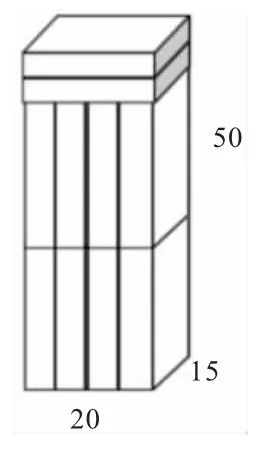
方案四的表面积：（20×15+15×50+50×20）×2=（300+750+1000）×2=4100（cm2）

师：有什么经验要分享给大家？比如怎么更快地得出方案？

生1：首先拿到一个长方体，它总共有三个不同的面。先把最大的面重合，尽量减少最大的面，这样就能减少包装纸。

生6：为什么方案四不是最简的呢？

生1：方案四的高接近长和宽的两倍，和正方体非常不相似，也没有把最大的面藏起来。

服务特点：I）在科学技术与医学领域内最权威的在线检索与获取全文的服务商之一，尤其是nature系列期刊、提供pdf预览功能；II）提供优先出版服务（快速，比纸本期刊更快看到最新的研究）；III）提供投稿、审稿服务（需登陆且需实际投稿才能一一体验）

生6：那为什么不把十个叠在一起？它们就是把最大的面藏起来的。

生1：十个叠在一起，虽然是把每个图形最大的面藏起来，但是叠到第五个就会产生新的大面，因为大面是随时会产生变化的。

师：比较这些答案，能找到怎样包装最节省材料的奥妙吗？

生：我发现，要表面积最小，它们的长、宽、高要接近一些。

生：第一个是藏大露小，尽量把最大的面藏起来，最小的面露出来；第二个是观察小的面会不会叠成更大的面；第三个是包装要接近正方体，长、宽、高越接近，表面积越小。

师：想最节约包装的材料，就要让长、宽、高尽可能接近，把它尽可能拼成一个正方体。

【赏析：“当老师理解数学的每个主要领域或主题的发展进程，以及基于它们的序列活动时，他们创设的数学学习环境就会特别具有发展适宜性和有效性。”儿童的学习与发展遵循自然的发展进程。从生生对话和师生对话中可以看出，学生经历了一个完整的探究过程，这一进阶过程完全符合SOLO 分类理论，从学生展现的作品，我们不难划分出以下五种思维水平。

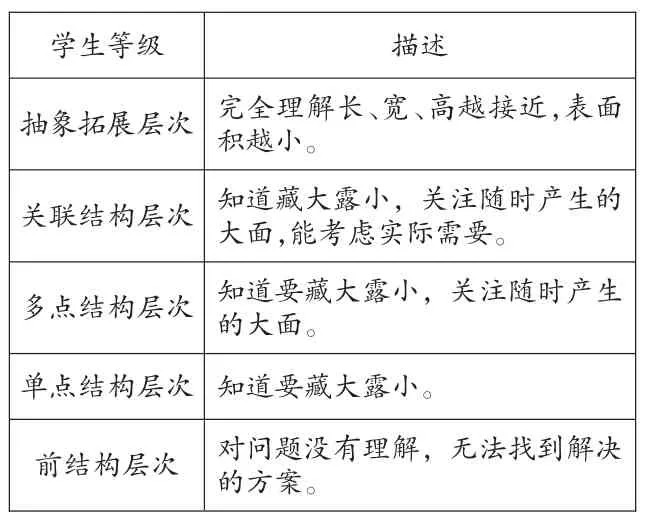
各个分数等级描述及学生表现

从十个大面重叠的简单操作到随时关注大面变化，藏大露小，再到不是最节约，但是有趣的，能结合实际需求，最后到长、宽、高尽可能接近，拼成一个近似的正方体。每位学生用自己的方式和适合的角度切入，沿着这条学习路径，拾级而上，最终一起达到最高的思维层次。

片断三：立体化的共通能力

师：通过这节课的学习，你有什么收获？

生：我知道了要听取别人的意见，从中可以得到更多的方法。明白了团队合作的重要性。

生：我学会了节约资源，节约包装就是爱护地球。

生：我知道包装要尽量把大的面叠在一起，然后长、宽、高也要接近，尽量变成近似的正方体。

师：大家还有没有新的问题想解决？

生：除了包装问题，还有体积、容积的问题。有的纸皮很厚，可能要算一下它们的容积。

生：生活中物体的形状复杂多样，可能还要学到不同物体的包装方案。比如去旅游时行李箱放不同的物体，就有空间利用率的问题。

生：生活中的包装还要更深入地研究纸皮的厚度和衔接处。

生：下次可能求的是把物体叠在一起，怎么镶边最节约材料。

师：其实关于包装还有很多数学问题，大家可以找一个最喜欢的问题继续研究。

【赏析：课堂上学生信息的来源和学习所得，并不是教师讲授的结果，而是同伴之间合作互助的成果。在交流中，学生从“最节约的方案”中跳脱出来，去思考更为广阔的包装中的学问，课程在交流中无限地延展，为后续的学习和研究提供了可能，也在学生的心里种下了热爱数学研究的种子。21世纪初，香港以“学会学习”作为课程发展路向，着手全方位课程改革。香港在中小学教育方法上更加注重师生之间、学生之间的互动。在课堂上，教师需要引导小组讨论，以小组为单位给出问题的答案，而在课后作业或测验考试上，也会运用更多项目式的形式，让学生以小组为单位共同讨论解决问题，并在课堂上给其他学生演示他们得出的答案，培养十项共通能力。我们可以从陈老师的课堂中对标这些共通能力，例如：道德教育、协作能力、沟通能力、创造力、批判性思考能力、运算能力、解决问题能力、自我管理能力以及研习能力等。通过这种互动式的教学，让学生发展更为立体化的共通能力。】

以能力来呈现核心素养是国际上一般的表述方式，带得走的能力则是核心素养。本节课我们可以看到陈老师以“包装”为活动载体，在探究的过程中，学生的运算能力、几何直观、推理意识、空间观念和应用意识都得到了很好的培养，有效地落实了核心素养。

最后，引用崔允漷教授的一段话作为总结：“如果说教育的目的（培养目标）是‘想得到的美丽’，那么课程标准就是‘看得见的风景’，而教学目标就是‘走得到的景点’，这种层级化、一致性的‘树人目标体系’，使‘看见的风景’既能对标‘想得到的美丽’，又能落实到‘走得到的景点’，加上每门课程的课程标准建构的素养导向的目标一族，将‘树人’过程从抽象的目的逐步分解为具体的目标，使得教师理解并践行从‘教书’走向‘育人’有了清晰的路径，立德树人根本任务的‘落实’有了清晰、可操作的凭依。”把“想得到”“看得见”变成“走得到”“带得走”，陈老师做到了。