数学史融入课堂教学的思考与实践

文|陈华忠

数学史涵盖着丰富的数学教育素材，数学教学应该从数学史中汲取养分，充分挖掘教材内外的数学史资源，丰富学生的文化底蕴，激发学生学习数学的兴趣，提高学生的数学素养。

一、借助数学史，凸显数学的文化底蕴

人教版教材中数学史内容的设计模式大致有两种：“习题引出数学史”和“阅读材料呈现数学史”，呈现方式只有文字和图片两种，形式较为单调。为此，教师在备课时要深入挖掘教材的文化价值，用好数学史，呈现数学文化，感受数学之美，激发学习兴趣。

1.展现数学史，让学生感受数学之美

徐利治指出：“数学教育与教学的目标之一，应当让学生获得对数学美的审美能力，从而既有利于激发他们对数学科学的爱好，也有助于增长他们的创造发明能力。”数学从表面上看是枯燥乏味的，然而却具有一种隐蔽的、深邃的美，一种理性的美。例如，在教学“回文数”一课时，教师借助数学史，精心选取“杨辉三角”中数字排列的特殊结构等，为学生建构对称结构提供情境素材，接着根据不同的内容，引导学生将“杨辉三角”中的数字排布与回文语句、棋盘中的棋子排序以及拱桥的对称结构进行对比，进而唤起学生对“对称”的内在审美感受，让学生在感受数学美的同时，激发他们探索数学的欲望，从而喜欢数学、热爱数学。

2.借助数学史，让学生感悟数学文化

数学只有真正回到生活中，才能显示其本身的价值和魅力。学生只有回到生活中运用数学，才能真实地显现其数学学习水平。借助数学史，作为一节课的结尾不失为一种好的利用方法，合理运用可以产生“余音不绝，绕梁三日”的效果。例如，在教学“分数的初步认识”这一单元时，可在最后介绍古代分数的表示方法，让学生体会到每一个数学概念或数学知识都是经过了漫长的发展和演变过程，才变成现在的形式，感受数学的文化价值。利用数学史进行课后拓展的方式有多种多样：一是故事形式，介绍数学家的逸闻趣事，一些有趣的数学典故等。二是数学游戏形式，如莫比乌斯带，让学生从游戏中学，从游戏中成长。三是习题形式，《九章算术》中的“盈不足问题”以及“百鸡问题”“龟鹤算”等都可做巩固提升的习题。四是数学专栏形式，可以在班级设立数学小专栏，由学生搜集材料，可以介绍数学家的生平和成就，也可以介绍历史上著名的数学问题或数学猜想，又或者是介绍一些使用律高的数学名词等，教师可以根据实际情况加以选择。

二、借助数学史，呈现数学的应用价值

1.融入数学史，激发学生学习兴趣

数学史可以有效地激发学生学习数学的兴趣，教师可以借助数学史帮助学生学习数学知识，掌握数学思想与数学方法。

例如，在教学四年级的“魔法莫比乌斯带”一课时，莫比乌斯带只有一侧沿着莫比乌斯带的中心线切割，它仍然是莫比乌斯带。沿着莫比乌斯带的第三条线切割，它是一对两个大而一个小的莫比乌斯带。利用莫比乌斯带的这些特性进行教学，可以让学生经历猜想与验证，在莫比乌斯带如魔术般的变化中，感受数学的魅力和乐趣，拓宽数学视野。在课内总结时，可以让学生回想自己生活中运用莫比乌斯带原理的现象，并用课件向学生展示瑞典的《不可能的图形》的邮票，播放有关中国科技馆耸立的三叶钮结的录像。这样，通过“魔术莫比乌斯带”教学，不仅激发了学生学习的兴趣，而且让学生感受到数学还能解决日常生活中的实际问题。

数学史融入课堂教学不是单纯地教给学生关于数学的历史知识，而是营造一种探研的课堂气氛，激发学生的学习兴趣，培养学生的探索精神。

2.应用数学史，促使学生理解新知

在数学课堂教学中，向学生介绍一些数学历史故事，有利于调动学生的学习积极性，从而积极参与，主动探究，让学生在轻松愉快的氛围中，学习新知，理解并掌握所学知识。

在教学“圆的认识”一课时，引导学生发现与学习圆的特征后，引用墨子的“圆，一中同长也”，让学生对古人的话进行解释，激发了学生探索圆的特征的欲望。在“画圆”这个环节，先展示学生“不圆”的作品，引导学生观察这些作品，并说道“圆的样子都是一样的，不圆的样子就各有各的不同”。教师幽默的评价引发学生欢笑之余，用一句古人的话“没有规矩，不成方圆”，激起了学生对“没有规矩”和“有规矩”的思维碰撞，学生都陷入了深入思考。当学生对画圆有了深刻的领悟之后，教师追问，将学生的思维推向了又一个高点，最后又回归到“圆，一中同长也”中来，这个数学史，让学生对圆的本质属性有了深层次的理解，更深入地领悟了数学的本质和方法，经历了数学学习的全过程，让学生直观、全面、生动地掌握了圆的知识。

3.引用数学史，培养学生数学思维

如果一个人毕业后没有机会使用在学校学到的数学知识，很快就会忘记它。只有数学精神、数学思想方法、研究方法、推理方法以及看问题的角度，却能随时随地发挥作用，使他们终身受益。数学知识具有双重性，即显性的知识和隐性的数学思想方法。数学史留下数学家处理数学问题的痕迹，它或隐或现地展现出有关数学的思想和方法，这些思想方法正是学生所要效仿的。而这些数学思想方法并不能简单地进行传授，它需要一个复杂的理解过程。数学史上典型的题材，就可以用来分析数学家发明发现的心智活动，对学生起到方法论的启迪作用。例如，欧拉将著名的哥尼斯堡城七桥问题抽象为一个用“一笔划”解决的问题，在解决七桥问题时，欧拉创造了新的概念，运用了一般化的方法，也使用了“转化”这一数学思想方法，善于运用“转化”的思想方法是数学家思维方式的重要特征之一。许多学生只知道如何解决问题，而不够重视解决问题后的反思。因此，当面对一个从未见过的问题或者是非常规性的问题时，学生往往是茫然的、无助的，无从下手。而学习数学家在解决未知领域问题时所使用的思想方法，对于学生的解决问题是非常有帮助的。

由于数学史可以开阔学生的视野，使他们认识到在探讨数学问题时，要突破思维的局限，形成良好的数学思维习惯，从而发展学生的数学思维。良好的数学思维，可以使学生快速整理数学知识之间的联系，找到题目所传递的信息，叙述思考的过程。借助数学史，可以促进学生数学思维的发展。

4.巧用数学史，拓宽学生知识面

数学课堂教学，不能满足于教给学生知识，更应致力于培养学生的数学素养，提高学生的人文素养。为此，学生不仅要掌握课堂所学知识，而且也要学习课外知识，拓宽学生的知识面。

例如，在教学“三位数乘两位数”一课时，课前，教师布置学生收集信息并理解“格子乘法”相关的知识。课尾，教师向学生介绍“格子乘法”——“格子乘法”是十五世纪中叶意大利数学家在《算术、几何、比及比例概要》中描述的两个数相乘的计算方法。当这种方法传递到中国时，被明朝数学家程大伟称为“法律算法”中的铺路锦。大家能否模仿934×314=293276 这个例子，并结合你课前了解的知识，尝试算一算37×256等于多少？

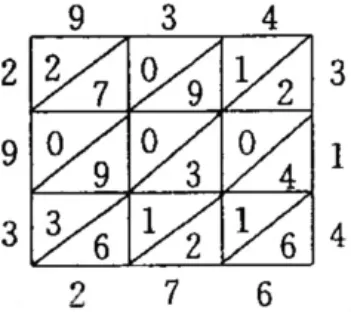
格子乘法和笔算乘法的计算方法虽然不同，但算理是相同的，结果也是一样的。向学生讲授格子乘法，可以让学生了解乘法的发展历史，了解不同的计算方法。这些数学史知识有助于拓宽学生的知识，理解数学的发展史。

三、借助数学史，凸显数学的育人价值

1.展现数学史，培养学生良好人格

数学史在学生人格的形成过程中能起一定的启发和促进作用。所以，教学时教师可以适时灵活地穿插介绍相关的数学史及数学家的事迹。例如，在教学“圆的周长”一课时，教师就可以介绍祖冲之的故事。又如，在教学“探究规律”时，教师也可以适时介绍高斯八岁发现定理、陈景润与哥德巴赫猜想等等，数学家的事迹，不仅可以为学生点起一盏理想的明灯，而且对学生长远学习目标的树立也起着促进作用。数学家那种坚持真理、严谨求实的科学态度，不畏艰难、乐于奉献的精神气质，能够有效地感染学生，激励学生克服困难、顽强拼搏。学习古今中外巨大数学成就，帮助学生认识数学是有价值的；学习历史著名数学问题，帮助学生认识数学是一个由问题和解决问题的方法构成的有机整体。数学是一门具有极强生命力的科学，它不断变化和发展，与人类社会的发展和进步息息相关。数学史与小学数学教学的充分融合是提高学生对数学的宏观认识、帮助学生树立正确数学观的有效手段。

2.活用数学史，培养学生爱国之情

中国数学的发展有着辉煌的历史，很多数学成就都走在世界前列。教师要深入挖掘教材中的爱国主义教育因素，激发学生民族自信心、自尊心、自豪感和爱国热情。为此，教学中教师要借助数学史，有机地渗透爱国主义教育。如，在教学“圆的认识”一课，教师讲述“墨子的发现比西方人早了一千多年……”时，学生的自豪感油然而生，为自己的祖国自豪，更为身为中国人而自豪！教学中教师还要深入挖掘数学史的价值，充分运用好数学史，为课堂点睛的同时有效地培养学生的爱国热情。

总之，教师要学会挖掘数学史，借鉴数学史，并应用好数学史。同时还要根据学生的实际情况，从多角度、多层次地将数学史融入课堂教学，激发学生的学习兴趣，拓展学生的知识面，培养学生的爱国情怀与数学核心素养。