基于改进多目标自适应遗传算法的机器人路径规划
张 铮, 柯子鹏, 周嘉政, 钱勤建, 胡新宇
(湖北工业大学 机械工程学院, 湖北 武汉 430068)
移动机器人是集环境感知,自主规划与自动执行任务的智能设备,通过预先的编程构建机器人内部控制系统。伴随机电一体化技术的快速发展,移动机器人受到广泛关注,其应用涵盖太空、军事、农业、医疗、快递、家庭等场合,对推动科技、社会发展,提高生活质量起重要作用。路径规划问题是在满足现有环境限制的前提下完成最优路径的规划。路径规划作为移动机器人至关重要的部分,成为现今机器人领域的研究焦点。
移动机器人发展的路径规划算法主要分为三种,第一种,传统路径规划算法,例如A*算法、图论算法等[1-4];第二种,基于采样过程的路径规划算法,主要为RRT算法与PRM算法[5-8];第三种,智能仿生路径规划算法,根据仿生设计出的神经网络算法、蚁群算法、遗传算法等[9-16]。
其中遗传算法是一种启发式搜索算法,相较于传统路径规划固定式求解,能保证最优解与效率的动态平衡。具有较好的全局最优搜索能力,但局部搜索能力差。通过各种方式改进遗传算法在机器人路径规划中应用广泛,并具有较多的研究成果。如文献[9]提出一种双重标准编码方式,增加遗传算法变异过程以避免局部最优解产生,对多目标路径规划高效适用。文献[10]将精英主义族系策略融入遗传算法中,利用精英标记遗传个体并引入多目标适应度评价函数以实现集群协同控制的需求。文献[11]为解决传统遗传算法缺点同时确保最优解质量,将路径拐点数量作为适应度指标。实现减少算法迭代次数与提高最优解质量。文献[12]根据模糊算法调整遗传算法参数用以提高寻优速度,引入余弦平滑度因子改善路径安全性。文献[13]采用并行GA对无人机进行路径规划,同时验证了并行GA较单GA有更快的速度与产生更好的结果,但对处理器有更高的要求。文献[14]使用退火算法结合遗传算法进行路径规划,以表面局部最优问题同时保证迭代过程中种群多样性。文献[15]采用粒子群算法结合遗传算法优化机器人运动规划,并将能耗与时间融入目标函数,以提高机器人性能。文献[16]提出改进混合蚁群遗传算法,以优化遗传操作与适应度函数,同时去除蚁群死锁问题,合理减少了迭代次数,并缩短了搜索时间。
在上述研究中,针对遗传算法的改进主要通过改进原始操作、结合其他优化算法进行缺点互补或引入相关操作实现,虽然在某方面具有较好的效果,但是增加了算法整体复杂度,延长了算法耗时,提高了硬件的适配要求,同时优化方向较为片面。本文提出一种改进多目标自适应遗传算法。通过限制性均匀随机搜索算法初始化种群,同时建立限制性步长对初始种群路径长度的先验模型。综合考虑路径长度,路径安全度与路径能耗搭建适应度函。利用平衡阈值改进自适应交叉变异算子以提高提高自适应交叉变异效率。提出自适应进化判断操作,以缩短种群进化停滞过程与放置种群进化倒退现象。最后引入删除操作去除最优路径冗杂节点来优化最优路径。经过与GA,ACO-GA、SSA算法对比实验,本文改进算法性能更具优越性,在降低算法复杂度同时,缩短了其迭代次数并加快了收敛过程,具有较好的鲁棒性,在维持最优路径长度的同时,降低了路径能耗。
1 环境建立
1.1 路径规划环境建模
由于栅格地图容易创建,表示与保存,每个位置对应点唯一,有助于机器人路径规划。故采用栅格地图对移动机器人环境进行建模,每块栅格的尺寸通过障碍物的大小与移动机器人的大小共同决定。
在栅格地图中利用黑块表示障碍物,白块表示无障碍物,并假设栅格地图周围全为障碍物。为方便仿真实验的进行,假设所有的栅格地图都为考虑机器人安全距离后扩展的环境,同时假设移动机器人为一质点,避免影响验证算法性能。栅格地图建立方式见图1。

图1 标记序号的栅格地图Fig.1 Grid map with serial numbers
1.2 编码方式
为减少直接用坐标计算带来的巨大计算量,故采用坐标到序号的映射转换来替代坐标计算。设栅格地图的大小rows×cols,按照1-rows·cols来表示栅格序号。序号与坐标的映射公式如下:
(1)
2 本文算法介绍
2.1 初始化操作
种群初始化在遗传算法中往往容易被忽略,初始种群的质量对算法整体迭代次数、最优解质量等都有巨大的影响。同时质量高的初始种群能极大减少遗传算法的收敛过程,以更快的速度达到最优解。本文提出使用一种限制性启发搜索算法结合中值插入算法用以初始化种群,节点生成库见图2。

图2 节点生成库示意图Fig.2 Schematic diagram of node generation library
该算法的具体操作流程如下:
1) 根据栅格地图的尺寸(rows,cols)计算出节点库数量,计算公式如下;
N=rows+cols-3
(2)
k=ceil(N/2)
(3)
2) 生成节点库,用以随机生成节点,如图2所示,节点库为45度方向上非障碍物的节点集合,每个节点库占据两斜层。总节点库表示为:
ccan={can1,can2,can3,……,cank}
(4)
3) 根据如下限制性条件在节点库中随机生成节点。若不生成不满足条件的节点,则重新在节点库cani中生成节点,并满足一定的循环次数。若超出训话次数仍不满足条件,则删除该路径。
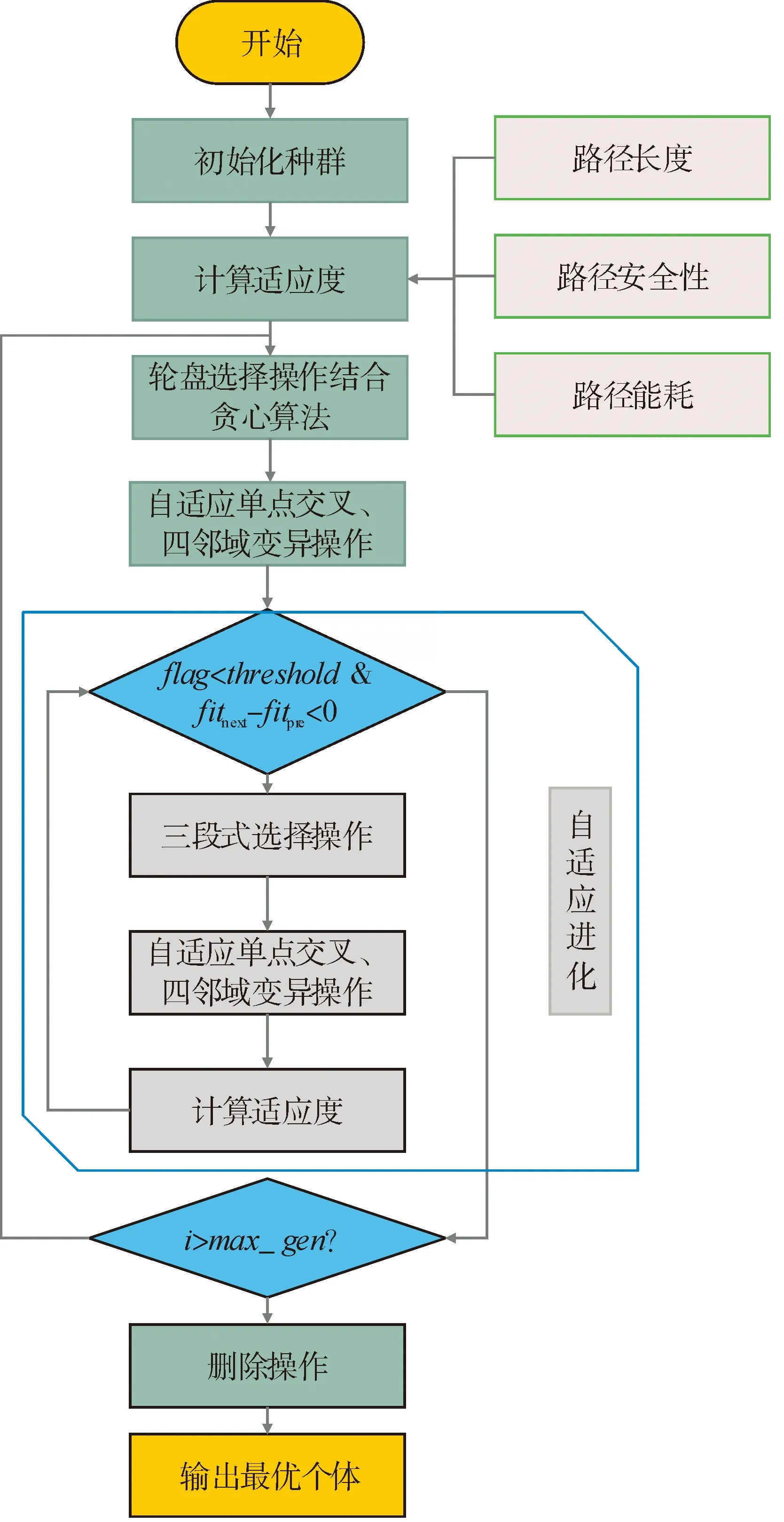
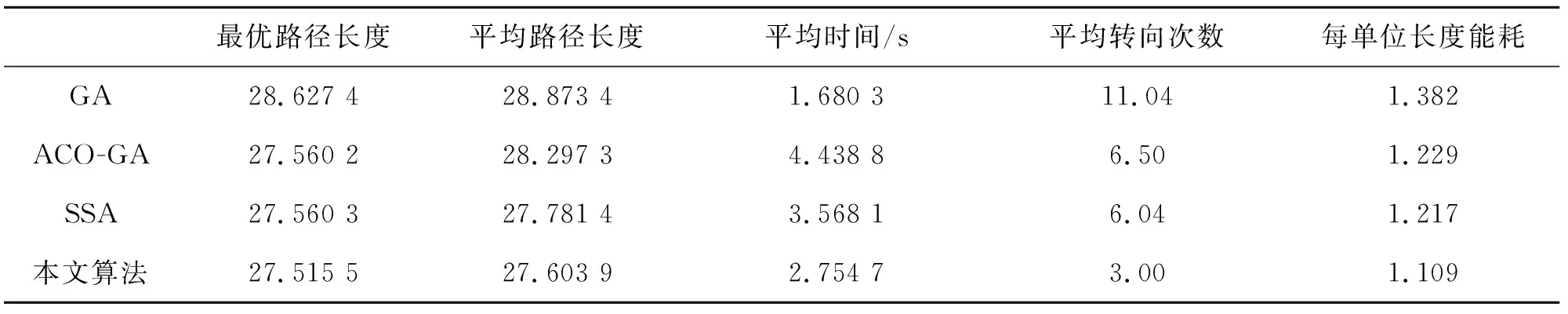
max(abs(xi-xi-1),abs(yi-yi-1)) (5) 4) 根据从节点库中生成的间断节点个体,利用中值插入方法使路径连续。插入的节点是通过向下取整相邻节点的平均值获取,同时判断该点是否为障碍物,若为障碍物,则通过4邻域移动寻找出非障碍物点。 (6) 5) 中值插入算法的终止条件如下,通过顺序节点的横纵坐标的最大距离以判断节点是相邻节点。 max{abs(xi-xi+1),abs(yi-yi+1)}≤1 (7) 限制性步长step对产生的初始路径长度length存在影响,通过最小二乘法建立限制性步长的先验公式。二次曲线拟合公式为: f(x)=ax2+bx+c (8) 式中:x为路径长度;f(x)为拟合的步长函数。 根据实际stepi与建立的拟合函数f(x)建立最小二乘目标函数如下: (9) 分别通过对a、b、c求导,列出如下联合算式: (10) 为提高拟合的准确性,通过每个step对应的多个步长的均值来反映两者之间的关系,见图3。 图3 拟合步长与路径长度Fig.3 Fitting step size and path length 拟合后的步长先验公式为: step=-0.00064x2+0.0519x-0.9058 (11) 适应度函数作为遗传算法中个体在既定条件下的适应状况指标,用以明确种群的进化方向。根据多目标适应度函数,可以从多个方面优化路径[17-21]。为减少机器人在路径规划中因转向过多造成的能耗损失,并在实现路径长度最优时保证路径安全性问题,本文将路径长度,安全度与能耗三个因素作为评判路径质量优劣的依据。适应度函数表示为: (12) 式中:D(k)是距离函数;S(k)是安全度函数;T(k)是转向次数函数;ρ1、ρ2、ρ3分别为三个指标对应的系数。路径的距离是根据邻近节点的欧式距离求和得出,距离函数为: (13) 式中k为路径的总节点数量。路径的安全函数如下,通过统计每个节点四邻域(见图4)的障碍物数量之和,判断该路径周围的障碍情况, 图4 四邻域图Fig.4 Four-neighbor graph (14) 与8邻域障碍物统计相比,四邻域障碍物统计可以有效避免斜穿障碍物现象,同时减少搜索过程,以保证较高的统计效率。 路径的转向函数见式(15),通过控制路径的转向次数,以提高路径的平滑度与降低路径能耗。 (15) 式中Ti为第二个节点开始的转向统计。由于单个节点无对比,无需进行判断,故从第二个节点开始判断,直至最优一个节点k。 路径的能耗通过路径长度与转向次数共同确定,能耗表达式为: (16) 选择操作是遗传算法中影响遗传方向的重要一环,必须考虑选择操作过程选出有潜力的最优个体,同时为防止结果陷入局部最优值。尽量维持路径的均匀多样化,以消除种群垄断。本文采用的选择操作为改进的轮盘选择操作与3段式选择操作。其中轮盘选择的随机性在迭代过程中保证每种个体都存在被选中的机会,以实现维持物种多样性。但由于轮盘选择操作过于随机,每次个体的选择不够稳定,进而影响遗传算法的迭代过程。这里结合贪心算法,将父代种群的最优个体分成两部分操作,一是直接保留父代最优个体,不放入选择操作结束后的种群,二是将最优父代个体直接放入选择操作后的种群。此种做法的目的是保留父代最优个体的同时,避免父代最优个体在子代遗传操作中丧失优势,以保证种群始终稳定不退化遗传。轮盘操作是通过每个个体的适应度值计算适应度占比。通过轮盘选择,重复抽取个体。每个个体的被随机选中的概率公式为: (17) 轮盘选择通过累加概率,随机选中相应的个体,其概率累加公式为: (18) 由于后续提出种群进化判断操作,在进化判断中使用三段式选择操作,提高算法运行速度同时,能加快种群收敛过程。其原理为,先将种群按照适应度大小排序,此时按照数量将种群分成低适应度,中适应度,高适应度。删除低适应度段,同时将一倍中适应度段与双倍高适应段放入选择后的种群中进行后续操作。三段式选择具体操作见图5。 图5 三段式选择操作Fig.5 Three-stage selection operation 交叉变异操作作为遗传算法中群体进化的主要操作,需要在维持种群多样性的同时,尽可能使得交叉后的群体优于交叉之前,同时保证获得更优种群与加快种群收敛速度。由于全自适应交叉变异概率对处于中等适应度群体的影响较小,同时增加了算法的计算复杂度,这里通过分段阈值thresh来平衡交叉变异概率自适应性与计算复杂度的影响。自适应方式主要分为两种,一是随迭代次数自适应变化;二是根据个体适应度大小自适应变化。第一种自适应方式受迭代次数的影响明显,虽然对遗传算法改进有一定效果,但因迭代次数限制,收敛速度提高有局限。第二种自适应方式不受迭代次数的影响,每次迭代都进行相同的自适应操作,根据个体适应度值更改其交叉率。本文采用不受迭代次数影响的自适应交叉操作,第一段针对适应度较差个体自适应提高其交叉变异概率,中间一段为数量最多的群体,采用固定的交叉变异概率,最后一段针对高适应度个体,通过降低其交叉变异概率以减小高适应度个体流失的概率。 (19) (20) 式中:fitmax为当前种群最大适应度;fitmin为当前种群最小适应度;fit(i)为个体i的适应度;thresh为概率分段阈值。交叉变异的自适应概率分布见图6。 图6 交叉变异概率自适应变化图Fig.6 Cross-mutation probability adaptive change graph 若随机数比自适应交叉率小,则个体进行单点交叉操作,交叉过程见图7,设待交叉的个体为a-b-c-d-e与a-b-g-h-e,设交叉点为第三个,则两个个体在节点3之后的节点将共同进行交叉。经过单点交叉后的个体分别为a-b-c-h-e与a-b-g-d-e。 图7 单点交叉过程Fig.7 Single point crossover process 变异操作是遗传算法模仿生物基因突变的过程,在路径规划中的变异操作常采用随机点的八邻域范围内随机突变。由于突变具有不定向性,无法控制变异本身以控制进化方向,若变异后的节点为对角邻域,同时四邻域存在障碍物,则易出现横穿障碍物现象,故采用四邻域变异。经过变异操作后的节点需要经过障碍物判断,以保证变异后路径的有效性。在一定搜寻次数条件下寻找出非障碍物点。若超出搜索次数,则停止操作以避免计算量过大影响整体速度。最后将变异后的节点通过中值插入算法与其他路径段连续连接。 四邻域变异的模板mask与其x、y方向上的算子如下。通过随机选取模板mask为1的位置,根据位置计算出x、y方向算子对应的值,用以更新变异节点的x、y坐标。 (21) (22) 为避免种群在迭代过程出现较多维持停滞或退化现象,采用自适应进化判断操作,用以判断种群的进化状况,若种群未进化,则通过进行多次遗传操作。利用threshold平衡阈值以平衡进化过程与进化耗时的影响。针对退化现象,通过贪心算法,保留局部最优个体,以防止种群进化出现震荡过程。经过遗传进化判断,进化判断公式为: iter (23) 式中:fitnext为子种群的最佳适应度;fitpre为父种群的最佳适应度;iter为自适应进化操作中的循环次数;threshold为自适应进化操作中的最大循环次数,以避免降低算法整体速度。 若每代子种群最佳适应度不小于父种群的最佳适应度,则经过三段式选择去除低适应度个体,再进行多次自适应交叉变异操作,并重新计算适应度,然后经过自适应进化判断。 删除操作为完善遗传算法最优个体的必要步骤,相应地图中初始节点的数量具有固定。虽然遗传算法实现固定节点的最优个体,但对少于固定节点数量的路径不一定具有优越性,因此为解决冗杂节点影响最优个体质量问题,通过删除操作实现个体去除冗杂节点以提高最优个体质量。删除操作前后的路径对比图见图8。 图8 无删除操作与删除操作路径Fig.8 No delete operation and delete operation path 该删除操作算法通过检测某节点的左右邻点是否能无障碍直线连接来判断该节点是否为冗杂节点。式(24)多次利用式(25),循环遍历中点的中点并判断是否为障碍物,若整个遍历过程都无障碍物,则返回无障碍物标志,表示当前节点的左右节点直线连接不经过障碍物,故可以删除该节点;若有一个中点被判断为障碍物,则返回障碍物标志,表示当前节点的前后节点直线连接会经过障碍物,故该节点不可删除。其判断表达式为: flag=delete_node(nodei) (24) (25) 式中:(xi-1,yi-1),(xi-1,yi-1)分别为判断删除节点的前后节点坐标;通过前后节点坐标的均值四舍五入取整为(mx,my),判断(mx,my)在栅格地图中是否为障碍物。 flag为全局标志位,且初始化为0。若flag返回为1表示经过障碍物,直接退出判断函数;若不经过障碍物,则继续判断节点nodei+1,直至倒数第二个节点nodek-1;若flag返回0表示不经过障碍物,则删除节点nodei,并重新计算个体节点总数,后续节点判断从删除节点的后一节点nodei+1开始删除判断,同样直至倒数第二节点nodek-1。见图8,红色路径为未删除节点的路径,蓝色路径为删除节点后的路径。 本文改进的多目标自适应遗传算法见图9。 图9 本文改进算法流程图Fig.9 Flow chart of the improved algorithm in this paper 先通过限制性均匀随机搜索算法生成初始种群,利用初始路径长度建立限制性步长的先验模型,并根据路径长度、路径安全性与路径能耗构建种群的适应度函数,以从多目标优化路径。然后开始遗传迭代过程,使用轮盘选择结合贪心算法维持种群多样性,同时保留当代全局最优个体。通过改进自适应交叉变异操作对种群进行节点更替。通过自适应进化判断操作,对持续未进化的种群进行多次遗传操作。采用三段式选择操作淘汰低适应度个体,再经过改进自适应交叉变异操作,最后重新计算适应度并判断种群是否进化,若出现进化则退出进化循环,否则重复以上进化循环过程。最后通过删除操作,优化最终路径并输出。 为了验证改进多目标自适应遗传算法的优越性,通过在配置Inter(R) Core (TM) i5-6200U CPU @ 2.30GHz (4 CPUs) ~2.4GHz的Windows 10系统笔记本中,运用MATLAB 2017b软件进行仿真实验。为了更好的展示各算法性能,本文算法与对比的GA、ACO-GA、SSA算法均采用自身最优效果参数。同时为体现算法整体的应用广泛性,通过不同维度的栅格地图与同纬度地图中不同数量障碍物分别设立50次对比实验。分别通过对比50次实验的最优路径长度,平均路径长度,平均耗时,平均转向次数,平均能耗等因素,比较算法的有效性。 见图10,在75障碍物的20×20地图中,改进GA算法路径较为波折,SSA算法路径较为平顺,但其规划路径长度较长。ACO-GA算法与本文改进算法规划路径较为相似,但在平滑细节上与整体路径长度上都展示更好的效果。见图11,在102障碍物的20×20地图中,GA算法仍然波折,相比而言,ACO-GA算法,SSA算法与本文算法路径更加平滑。在节点细节上,本文算法具有更好的效果。 图10 四种算法在75障碍物的20×20地图中的规划路径Fig.10 Four algorithms for planning paths in a 20×20 map with 75 obstacles 图11 四种算法在102障碍物的20×20地图中的规划路径Fig.11 Four algorithms for planning paths in a 20×20 map with 102 obstacles 四种算法经两幅地图路径规划,其迭代过程见图12。GA算法在迭代过程具有较差的稳定性,同时需要较多的迭代次数达到最优规划,ACO-GA算法在规划路径时,稳定性不足,而SSA算法在迭代过程中具有较好的稳定性,相比而言,本文算法迭代过程更加稳定,同时以更少的迭代次数达到最优规划。 图12 四种算法在75与102障碍物地图的迭代过程Fig.12 Iterative process of four algorithms in 75 and 102 obstacle maps 四种算法在两个地图路径规划的统计数据见表1和表2,通过对比发现,本文算法规划的路径最优长度与平均长度均优于其他算法,并具有更小的转向次数,以优化机器人因过多转向而增加耗能。 表2 障碍物为102的20×20地图Tab.2 20×20 map with 102 obstacles 本文提出一种改进初始化操作的遗传算法进行路径规划研究,通过提出一种限制性均匀随机搜索算法结合中值插入算法提高初始化种群质量,并根据限制步长与产生的种群长度建立限制性步长的先验模型。在适应度函数中同时考虑路径长度、路径安全性与路径能耗。优化了自适应交叉变异操作,通过平衡阈值优化其性能。并引入了自适应进化操作结合贪心算法,以缩短种群进化停滞现象和防止进化倒退现象。最后删除操作,去除冗余节点,平滑路径。改进后的遗传算法在保证最优路径同时,能耗较低,其迭代过程更加稳定,具备良好的鲁棒性,能以更少的迭代次数达到收敛。但是,本文算法针对多目标的参数配置有待进一步优化。算法的速度有待进一步提高,同时只适用静态全局路径规划,后续可通过与实时动态局部路径规划结合,完善本文算法。
2.2 适应度函数

2.3 选择操作

2.4 自适应交叉变异操作
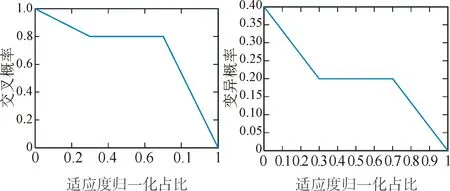
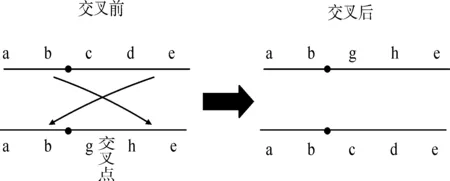
2.5 自适应进化判断操作
2.6 删除操作

2.7 本文算法流程
3 仿真实验



4 结 论

