基于XGBoost的堆场软土渗透系数反演研究

林玉祥, 林浩东, 莫品强, 褚 锋, 庄培芝

(1.中交第三航务工程勘察设计院有限公司, 上海 200032; 2.中国矿业大学 深部岩土力学与地下工程国家重点实验室, 江苏 徐州 221116; 3.山东高速建设管理集团有限公司, 山东 济南 250098;4.山东大学 齐鲁交通学院, 山东 济南 250002)

随着连云港沿海开发规划政策的落实,对连云港海积软土工程特性的研究逐渐引起业内人士的关注,其中土体渗透特性的研究为当前热点之一。渗透系数k是能定量反映土体渗透性强弱的重要指标,其数值的准确确定对渗透特性研究至关重要。渗透系数可由土工试验或现场井孔抽注水试验获得,但试验过程均比较繁琐且耗时耗力。因此,业界学者长期致力于提出一种简单可靠的渗透系数确定方法。

国内外学者对粗粒土的渗透特性研究较多[1-2],基于天然土物性指标、粒径级配曲线等,提出了大量渗透系数的经验公式。然而,相关公式通常不适用于细粒土,限制了其在实际工程中的应用。为了得到适用于广泛土类的渗透系数计算方法,部分学者利用静力触探可以连续反映土层性质的特点,基于静力触探数据对渗透系数进行预测计算。Robertson[3]提出了渗透系数与土类指数Ic的平均关系,并给出了通过静探数据计算Ic的公式。Elsworth等[4-5]和Chai等[6]分别结合球面流和半球面流模型,采用位错理论进行推导,得到了静探测试数据与渗透系数的理论关系式。李镜培等[7]基于前人研究成果提出了圆柱面径向渗流模型,推导出了修正后的经验公式。此外,有学者在渗透特性研究中引入机器学习算法,取得了一定成果。许增光等[8]基于实测电阻率,采用BP神经网络对土体渗透系数进行预测,通过计算实例证明了相比经验公式,神经网络法的平均误差更小。徐丽等[9]借助极限学习机建立渗透系数与水头之间的映射关系,并结合遗传算法构建了渗透系数反演分析模型。Zhao等[10]使用测井数据作为输入,训练了7种机器学习模型以预测珠江口盆地低渗透砂岩的渗透率,其中,XGBoost模型性能最优。Tian等[11]通过对3种特征选择方法和6种机器学习模型的比较分析,提出了一种将数字岩石物理模型与机器学习模型相结合的方法来改进地下多孔介质的渗透率预测。Pham等[12]基于越南岘港项目勘察数据构建土体渗透系数预测模型,并对采用的3种机器学习算法进行了比较分析。综上,前人多致力于对已有经验公式的修正或只与机器学习算法进行简单结合,而缺少对原始数据的合理利用和预处理分析;此外,已有经验公式或反演模型鲜有考虑渗透系数在水平向和垂直向的差异,而方向问题在实际应用中往往不可忽略。

本文根据土体静力触探数据与其渗透特性间的关联性,基于XGBoost机器学习算法构建一种渗透系数反演模型。该模型通过对原始数据的预分析选取特征参数和标签值,根据工程数据集的特点调整超参数,且考虑渗透系数在水平向和垂直向的差异。最后根据连云港开展的大荷载矿石堆场深厚软土地基加固研究项目的工程勘察数据,将本文模型与BPNN模型和前人经验公式进行对比分析。

1 XGBoost反演模型

1.1 XGBoost算法

极限梯度提升算法(Extreme Gradient Boosting, XGBoost)(后文简称XGB)在普通树模型基础上改进算法以提高精度,充分调用CPU的多线程并行以使提升树达到自身的计算极限,是近年来性能最强的机器学习算法之一[13]。

基于梯度增强决策树算法,XGB最小化目标函数至期望范围,预测值计算公式为:

(1)

目标函数计算公式为:

(2)

最小化目标函数,经过正则化项对算法学习权重的平滑,最终得到目标函数的最优解:

(3)

XGB允许使用者根据实际使用场景调整损失函数,对于渗透系数预测这样的回归问题而言,采用最小二乘损失函数:

(4)

XGB算法本质是基于梯度提升树实现的集成算法,涉及参数极多。考虑到使用的数据集较为简单,故仅对属于集成算法和弱评估器的部分重要参数进行调参(见表1),将其它与提升模型性能无关的复杂参数设为默认值。

表1 XGBoost算法重要参数表(部分)Tab.1 Important parameters of XGBoost algorithm (part)

1.2 考虑kv和kh的差异

在研究渗透系数水平向和垂直向的差异时,Bear[14]利用径向渗透仪装置将两种标准的垂直测量值(kv)与水平值(kh)进行了比较,提出了软黏土kh/kv的可能值范围:1～1.5(均质沉积物),2～4(发达宏观结构),3～15(明显分层)。以往的渗透系数经验公式往往不考虑渗透系数在方向上的差异,本模型将在前人研究基础上,分别对kv和kh进行预测,以使预测结果更符合工程实际。

2 工程应用

2.1 工程概况

场地位于连云港港旗台作业区南部,已由30万t航道二期疏浚土吹填成陆(工程范围内),土体地下深度约4 m内均为吹填土。孔压静力触探试验(CPTU)采用荷兰Geomil静力触探试验设备,试验结果如图1所示(以JT33静探孔为例)。

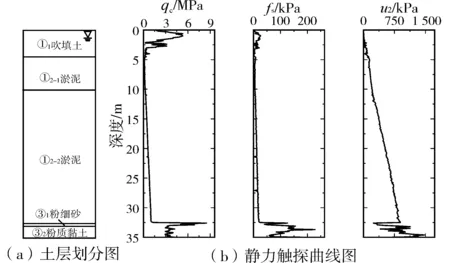
图1 Geomil静力触探试验结果(锥尖、侧壁、孔压)Fig.1 Geomil cone penetration test results (cone tip, side wall, pore pressure)

工程布置有静力触探试验孔65个、取土试样钻孔15个,且每个钻孔都与一个静探孔相邻。根据取土钻孔的位置及取土土样的深度匹配其对应的静探孔数据,建立CPTU数据与室内试验结果的严格对应关系。室内土工试验共设置了11组垂直向渗透系数(kv)和8组水平向渗透系数(kh)测定试验,以“QT钻孔号-土样编号”的形式命名土样,试验结果如表2所示。

表2 土工试验渗透系数数据集Tab.2 Permeability coefficient data set of geotechnical test

本工程钻孔取得的土试样等级为Ⅰ～Ⅱ级,即扰动程度为不扰动～轻微扰动。土样的采取、蜡封、储存、运输及室内试验严格按照有关规定执行,因此认为室内土工试验结果较为可靠。

2.2 XGBoost模型的训练与预测

2.2.1 输入变量和标签值的选取

由于静探孔的探测精度为0.1 m,即随深度变化每0.1 m可得一组CPTU数据,为将其与渗透系数测定值对应,假定土样的取土深度范围内每0.1 m的土层渗透系数都等于该段土样的渗透系数值。对CPTU数据的异常值进行剔除后,最终总数据集共有47组CPTU-kv数据和41组CPTU-kh数据。模型的输入变量从CPTU测试指标中选取,根据经验,考虑使用静探数据转换后得到的归一化锥尖阻力Qtn和归一化摩阻比Fr的组合,或直接使用土类指数Ic作为输入变量对标签值进行预测,相关计算公式[15]为:

Ic=[(3.47-lgQtn)2+(lgFr+1.22)2]0.5

(5)

Qtn=((qt-σv0)/pa)×(pa/(σ′v0))n

(6)

Fr=fs/(qt-σv0)×100%

(7)

式中:n为应力指数,n=0.381×Ic(RW)+0.05×(σ′v0/pa)-0.15;σv0、σ′v0分别为总上覆土压力和上覆土有效应力;qt为孔压修正锥尖阻力,qt=qc+(1-a)u2,a为探头面积比,取0.8;pa为参考压力,pa=100 kPa=0.1 MPa。

对于标签值的选取,考虑到表2中渗透系数的数量级均在10-2以下,故对渗透系数取对数,将其作为标签值,并以原数值设置对照组进行对比。

本文算法均通过Python的XGBoost模块来实现。采用默认超参数值建立预分析模型,对两类输入变量和两类标签值(以kv为例)形成的4种预测组合分别进行训练预测。以R2为评价指标,取模型运行5次结果的均值,如表3所示。

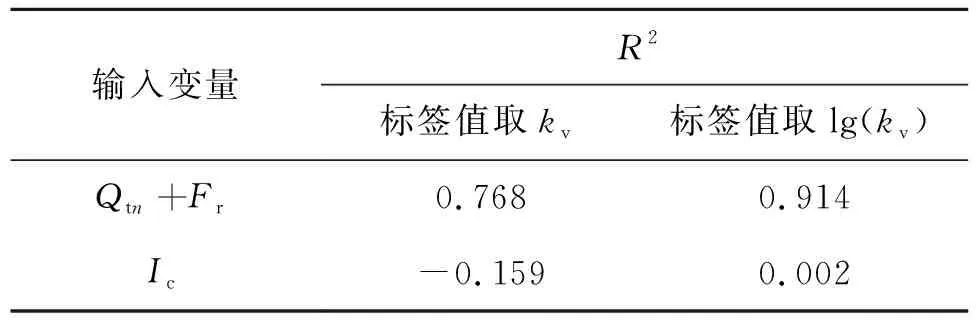
表3 预分析结果表Tab.3 Results of pre-analysis

从表3中可见,以Qtn+Fr作为输入变量、lg(kv)作为标签值时,R2最高。可见Qtn+Fr比Ic单值能更全面地反映土体的性质,更适合模型学习;渗透系数原数值过小且接近,将其作为标签值不利于模型分辨,在取对数后模型预测效果有较大提升。所以最后选取Qtn+Fr作为输入变量、渗透系数的对数值作为标签值建立预测模型。

2.2.2 模型的训练

1)kv预测模型

本模型的调参策略:先通过学习曲线调整弱评估器数量,再通过网格搜索调整其余超参数。将总数据集按7∶3的比例随机划分为训练集和测试集,为保证严谨性,只对训练集而非全集使用K折交叉验证来估计模型的泛化误差。考虑到样本数据量小,取K=5。模型的学习曲线图(以R2为评价指标)如图2所示。

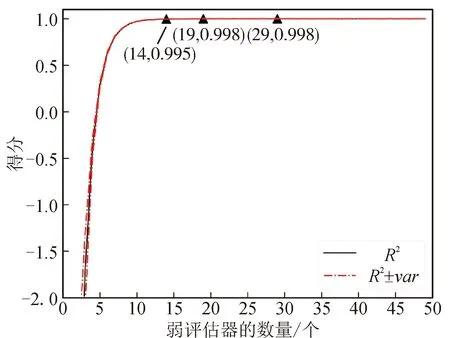
图2 训练集学习曲线图Fig.2 Learning curve of training set

图2中,R2、方差、总泛化误差分别在弱评估器数量为29、14、19时达到最佳取值,故最后取num_round=19。经过网格搜索对其余参数进行调整后,确定了一组最佳的超参数组合如表4所示。

表4 kv预测模型的最佳超参数Tab.4 Optimal hyperparameters of kv prediction model

设置该组超参数,采用经训练集训练的模型作为预测模型对测试集进行预测(见图3)。图3中,该模型对测试集的预测值与实测值的决定系数R2达到0.932,意味着模型的输入变量即归一化锥尖阻力Qtn和归一化摩阻比Fr对渗透系数的对数标签值有较强的解释性。注意到模型对k=10-3cm/s左右的砂土和k=10-7cm/s左右的软土均有不错的预测表现,说明模型对砂土和软土都能适用,泛化性较强。

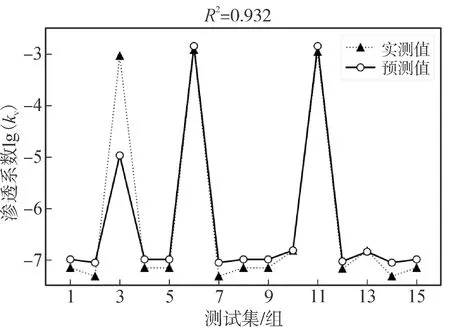
图3 kv预测模型结果可视化对比Fig.3 Visual comparison of results of kv prediction model

2)kh预测模型

与kv预测模型类似,经过学习曲线和网格调参后,确定了一组适用于kh预测的最佳超参数,如表5所示。

表5 kh预测模型的最佳超参数Tab.5 Optimal hyperparameters of kh prediction model

该模型在测试集上的表现见图4。图4中,因砂土水平向渗透系数数据较少,故模型对砂土的渗透系数预测效果略有下降,对软土预测效果仍较好。总体实测值与预测值的R2为0.891,仍为较高水平。

2.2.3 模型预测效果

将上述kv和kh预测模型应用于项目CPTU数据集,将土工试验结果的实测值与模型预测值直接进行对比,如图5所示。

图5中,考虑到工程实践中渗透系数的计算可接受一个数量级范围内的误差[16],故加入距实测值一个数量级的两误差线,该范围内的预测值都认为达到精度要求。为每个取土孔及土样编号指定特定符号,将该土样深度范围内每0.1 m对应的渗透系数预测值显示在对比图中,该深度范围内渗透系数的平均值以较大的符号显示。从图5可见,除了-lg(k)=3附近的两个数据在误差范围外,其余数据的预测值均与实测值较为接近。两个不准数据来源于QT06-101、QT14-02土样,均为砂土,这可能与土工试验结果中砂土数据较少有关,但该土样深度范围内渗透系数预测值的平均值与实测值相当接近。在测试集上,kv和kh的实测值与预测值取对数后的R2分别为0.932和0.891,均达较高水平。

3 各预测方法结果对比

3.1 Robertson经验公式

Robertson[3]提出了一种土壤渗透系数k与土类指数Ic的平均关系式,实测值在该经验公式图中的分布情况如图6所示。

图6 实测值k-Ic分布图Fig.6 k-Ic distribution of measured values

图6中,由于数据量较小,实测值与公式曲线离散度较大。将Robertson公式的计算值分别与实测值的垂直向和水平向渗透系数(取对数后)进行比较,垂直向的R2为0.330,水平向的R2为-0.022(R2为负意味着预测值的预测效果还不如实测值的均值),总体R2为0.282。注意到垂直向的R2远高于水平向,说明Robertson公式可能更适合预测kv而非kh。

3.2 (半)球面流模型经验公式

Elsworth等[4-5]、Chai等[6]、李镜培等[7]分别结合球面流、半球面流、圆柱面径向渗流模型推导出了CPTU测试指标与水平向渗透系数之间的理论关系式,其适用于正常或轻微超固结的黏性土和松散的无黏性土。将CPTU测试指标和探头参数代入上述各经验公式,将计算值与土工试验结果的水平向渗透系数实测值进行对比,如图7所示。

图7 预测值与实测值对比图Fig.7 Comparison of predicted and measured values

图7中,三个经验公式的计算值与实测值取对数后的R2分别为-3.290、0.571、0.505,可见,经典Chai公式表现最好。

3.3 BP神经网络模型

BP神经网络虽然性能上比XGBoost和随机森林等树模型稍逊,但优势在于结构简单,能够提取出较为简洁的公式以供使用。训练过程不再赘述。

将kv和kh预测模型的权值和阈值参数在三层BP神经网络中反算出来,代入提取公式可得:

(8)

lg(kh)=-0.79·tansig(-0.29·Fr+

2.67·Qtn+1.99)-1.66·tansig(2.47·Fr-

1.62·Qtn+0.98)-0.08·tansig(-0.65·Fr+

2.16·Qtn-2.67)+0.15

(9)

将CPTU数据代入上述公式计算,并将结果反归一化后可得渗透系数的BPNN预测值。 将实测值与预测值直接进行对比,如图8所示。

图8 BPNN模型预测值与实测值对比图Fig.8 Comparison of predicted and measured values of BPNN model

总体来说,BPNN预测模型对kv预测效果较好,R2为0.824,对kh预测效果较差,R2为0.612。

3.4 各预测方法结果对比

将基于CPTU数据的各预测方法所得预测值与土工试验实测值进行对比,如表6所示。

表6 各预测方法预测值与实测值对比表Tab.6 Comparison of predicted and measured values by each prediction method 单位: cm/s

表6中,取土孔所取土样的淤泥、粉质黏土、细砂、粉砂作为均质沉积物,渗透系数实测值都基本符合kh/kv=1～1.5。XGB模型的预测值也符合该相关关系,但BPNN模型的kh预测值普遍低于kv预测值,所以选择XGB模型进行渗透系数预测更合理。

计算各预测方法的计算值与实测值(取对数后)的距离,使用R2、均方误差MSE、均方根误差RMSE、平均绝对误差MAE、平均绝对百分比误差MAPE 5个常用评估指标进行评价,以R2为主要评价标准降序排序,如表7所示。其中,对于机器学习预测模型,则根据测试集而非全集的表现进行评估。

表7 各预测方法计算值与实测值距离的评估指标Tab.7 Evaluation indexes of distance between calculated and measured values by each prediction method

从表7中可见,基于XGB的kv预测模型表现最好,其次是基于XGB的kh预测模型。基于BP神经网络的预测模型表现虽然不如XGB模型,但也优于其它经验公式。前人的经验公式中,Chai公式有着最好的预测表现。由于本文所用数据集的数据量有限,在其他地区的土壤渗透系数预测中,XGB预测模型不一定能有如此表现,但对于连云港地区类似吹填土区域的渗透特性研究,还是有一定的参考价值。

4 结 论

1) 本文根据土体的CPTU数据与其渗透系数之间的关联性,提出了一种基于XGBoost机器学习算法的渗透系数反演模型,该模型适用于广泛土类,且考虑了水平向和垂直向渗透系数的差异。

2) 通过对输入变量和标签值的合理选取以及对最优超参数组合的确定,模型最终达到了较高的预测精度。该XGBoost预测模型的kv预测值与实测值的R2可达0.932,kh预测值与实测值的R2可达0.891,远高于传统的BPNN模型和前人经验公式。

3) 本文的工程实例表明,基于机器学习算法构建的XGBoost模型合理可行。XGBoost模型学习速度快、预测精度高、需调参数少,适合复杂原理相关的土体参数反演,对于渗透特性研究具有一定的参考价值。