基于PER-MATD3的多无人机攻防对抗机动决策

符小卫，徐哲，朱金冬，王楠

1.西北工业大学 电子信息学院，西安 710129

2.西安应用光学研究所，西安 710065

3.航空工业沈阳飞机设计研究所 体系部，沈阳 110035

自主空战对抗决策是无人机（Unmanned Aerial Vehicle， UAV）走向智能化必须研究的课题［1］。双方无人机根据观测的态势信息，如何快速做出有利于自身的机动动作以使得在对抗过程中尽量保存自己和消灭目标，是提升无人机智能化对抗水平的关键［2］。多无人机间攻防对抗将成为未来无人机间智能作战的主要模式之一，对其进行研究具有深刻的现实意义和必要性。多无人机对抗是指攻防双方进行多对一或多对多的对抗，本文选取多架防守无人机和单架具有高机动性能力的进攻无人机的对抗场景，研究并设计多架防守无人机协同拦截进攻无人机的机动策略。

学者针对多无人机间对抗过程提出了各种不同的研究方法来解决其机动决策问题。在传统决策方法中，主要包括比例导引法、人工势场法、几何学法、微分博弈法等。文献［3］为了避免无人机导引到敌机攻击范围内，提出一种基于数据链的变结构对抗导引方式。比例导引实现容易，计算速度快，但其数学模型方法不能适应于有障碍及威胁的复杂强对抗环境中，并且一般需已知目标运动方式，扩展性比较差。文献［4］将目标和障碍物的速度引入人工势场法中，使得无人机在动态环境下实现避障及目标跟踪。人工势场需提前了解环境信息，且一般容易陷入局部最优。文献［5］利用阿波罗尼斯圆法来研究不同对抗条件下多追捕者追捕单逃逸者的成功捕获条件。几何学法一般假定对抗双方能够获取所有对抗信息，且双方初始状态对机动决策影响极大。文献［6］通过构建微分博弈模型研究多无人机捕获单一目标的机动决策算法。微分博弈方法以数学公式形式描述对抗模型，有着严格的推导过程，然而求解过程随着对象数量增加变得十分困难。上述方法在实际条件中存在各自的局限性问题，与实际条件很难对应，无法在多机对抗的复杂高动态场景下取得较好的应用效果。

智能优化算法的发展使得学者们尝试将其引入多无人机对抗问题研究过程中，如仿生学［7］、群体智能算法［8］以及强化学习等。多智能体强化学习作为一种新型的人工智能算法，具有模型简单、自学性强、鲁棒性高等特点，近年来有不少利用该方法研究多无人机对抗领域的相关问题，展现较好的应用前景。文献［9］提出了一种基于强化学习和追逃双方运动规划策略的层次化框架方法，该方法可以使追捕者有效避开障碍物捕获移动目标；文献［10］基于多智能体强化学习算法，研究了多无人机的协同攻防对抗决策方法；文献［11］设计了3种不同的实验场景，利用多智能体深度确定性策略梯度（Multi-Agent Deep Deterministic Policy Gradient， MADDPG）算法训练机器人实现了对目标的围捕；文献［12］对MADDPG算法在奖励函数及网络结构上做出改进，提出了解耦多智能体深度确定性策略梯度（DEcomposed Multi-Agent Deep Deterministic Policy Gradient， DE-MADDP）算法用来解决多无人机协同围捕快速目标的追逃问题；文献［13］提出了一种基于 MADDPG 的多无人机协同任务决策方法；文献［14］提出了一种基于双延迟深度确定性策略梯度（Twin-Delayed Deep Deterministic policy gradient， TD3）的无人机近距空战格斗自主决策模型，并设计了基于价值的样本优先度排序方法，提升算法的收敛速度；文献［15］提出了一种相关经验学习的DDPG算法以解决拒止环境下无人机运动规划问题；文献［16］设计了基于TD3的无人机机动决策算法；文献［17］基于TD3的算法以解决无人机在有多个动态障碍物环境下的路径规划问题；文献［18］提出了一种基于改进TD3的无人机反追击机动决策算法。以上文献均利用强化学习算法对各自提出的问题进行研究及改进，然而针对复杂真实环境下的多无人机对抗研究较少，并未考虑无人机的避障探测能力和火力打击能力，在多智能体算法的性能方面还有值得研究的内容，例如如何在已有的训练算法基础上继续改进完善，使得算法的收敛性更快、稳定性更好。

本文主要针对存在障碍物的复杂环境下多无人机攻防对抗问题，在考虑无人机雷达探测范围和火力打击范围的情况下，利用深度强化学习算法开展无人机攻防对抗机动决策方法的研究。主要是针对现有较流行的MADDPG算法中存在值函数高估问题，将单智能体TD3算法扩展到多智能体领域，提出了多智能体双延迟深度确定性策略梯度（Multi-Agent Twin Delayed Deep Deterministic policy gradient， MATD3）算法，缓解了值函数高估问题，从而提高了算法收敛速度；为了进一步加快算法的收敛速度、提升算法的稳定性，提出了优先经验回放多智能体双延迟深度确定性策略梯度（Prioritized Experience Replay Multi-Agent Twin Delayed Deep Deterministic policy gradient， PER-MATD3）算法。

1 问题描述与建模

1.1 多无人机攻防对抗

如图1所示，多无人机攻防对抗场景可以描述为在有限平面区域内，存在1架蓝方进攻无人机和3架红方防守无人机，进攻无人机的任务是从初始位置（左上角）突破防守无人机的阻拦到达红方基地区域（右下角圆形小旗区域）；而防守无人机的任务是从初始位置（右下角圆形小旗区域）去拦截并击毁进攻无人机。无人机通过机载激光雷达探测环境中随机分布的大量圆形障碍物，无法提前获知障碍物信息。假设防守无人机均载有通信数据链，并通过己方雷达站能够实时检测敌机的位置信息及友机的状态信息，具有一定的协同能力；假设进攻无人机提前知道地面目标区域位置，并通过携带的GPS和电子陀螺仪获取自身状态信息，但无法提前锁定防守无人机的位置信息，只能通过激光雷达观测获取防守无人机的相对位置。本研究的假设条件可以更好的贴近实际攻防对抗场景。

图1 多无人机攻防对抗场景Fig.1 Multi-UAVs attack-defence confrontation scenario

图1中，a和dn(n=1，2，3)分别代表进攻无人机和防守无人机；sip=(xip，yip)(i=a，dn)表示双方无人机的位置坐标；sid=ψi(i=a，dn)表示双方无人机的航向角；siv=vi(i=a，dn)表示双方无人机的速度大小；stp=(xtp，ytp)表示目标区域中心点的位置；表示第k个障碍物中心点的位置。

1.2 无人机运动学模型

为了开展对攻防双方无人机对抗机动决策的研究，规定无人机的运动学方程为

式中：ai和ωi作为无人机的控制量，分别表示无人机的加速度大小和角速度大小；i=a，dn。

无人机的运动需要满足一定的运动约束，因此其状态量及控制量分别满足式（2）和式（3）：

式中：xmin和xmax分别为战场边界的最小横坐标和最大横坐标；ymin和ymax分别为战场边界的最小纵坐标和最大纵坐标；vimax为无人机的最大速度；aimax为无人机的最大加速度；ωimax为无人机最大角速度。

假设无人机当前时刻t的状态信息为在仿真步长ΔT内，在加速度大小ai及动作量ωi的作用下，其自身状态量会发生改变，下一时刻t+1的状态由状态转移方程确定为

1.3 雷达探测模型

假设双方无人机均装置激光雷达，其探测情况如图2所示。

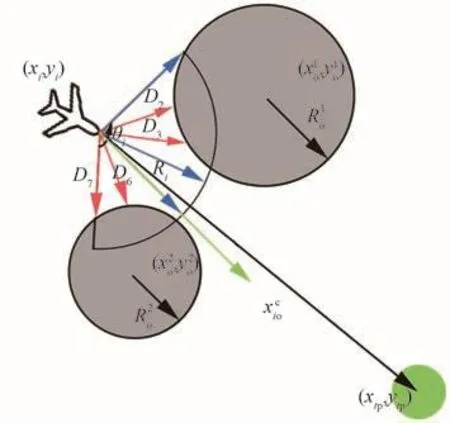
图2 无人机雷达探测模型Fig.2 UAV radar detection model

由图2可知，第k类圆形障碍物的半径为Rko(k=1，2，…，Nt)，其中Nt为圆形障碍物类型数量；第k类障碍物的数量为Nk，障碍物的位置为(k=1，2，…，No)，其中，No为障碍物的总数量；无人机雷达探测的角度范围为θi(i=a，dn)；无人机雷达的最大探测距离为Ri(i=a，dn)。为了更好地描述无人机对环境的感知，将无人机雷达探测角度范围等间隔地离散化为（ll=7）个方向，在图中用7条射线表示，每条射线长度为Dm(m=1，2，…，l)。最长射线的长度为无人机雷达的最大探测距离，其他射线的长度为无人机在相应方向上探测到的与障碍物或边界的相对距离。定义xmio(i=a，dn；m=1，2，…，l)为Dm与无人机雷达最大探测距离的比值，若该值越接近1，则表明无人机在该方向距离障碍物或边界越远；反之该值越接近0，则在该方向距离障碍物或边界越近。即无人机对障碍物的探测状态量可表示为

进攻无人机a在执行任务前，有一个已知的目标位置[xtp，ytp]，为了简化无人机输入状态维度，可将目标的位置信息合并到无人机的雷达探测信息中。具体地，在sao中找出状态量(m=1，2，…，l)最大值所对应的方向（可能存在多个，如图2中3个最长射线方向），然后在这些方向中选择与无人机-目标视线方向夹角最小的那个方向记为最优航向ψopti（如图2中射线方向），将该方向上的探测状态量记为这样就可将目标的位置信息合并到无人机的雷达探测信息中，后续可以利用合并后的信息使得无人机避障及靠近目标。

2 基于多智能体强化学习的多机攻防对抗

2.1 多智能体强化学习算法

在多智能体强化学习领域中，由于每个智能体均在环境中不断学习改善自身策略，从每个智能体的角度看，不清楚其他智能体的动作策略，而这些智能体的动作会对环境带来变化，导致环境变得不稳定，因此多智能体强化学习的难点在于不仅需要了解每个智能体与环境的交互过程，还需要考虑到其他智能体对环境的影响，使得问题变得较为复杂［19-20］。

在多智能体领域中，每个智能体与环境的交互过程被定义为马尔可夫博弈［21］（Markov Game），也被称为随机博弈（Stochastic Game）。假设环境中存在N个智能体，马尔可夫博弈可用多元组{N，S，A，O，R，P，γ}表示。其中，S为环境状态空间，用s∈S表示环境状态；O={O1，O2，…，ON}为智能体对于环境的观测量空间，其中Oi表示智能体i的观测量空间，用oi∈Oi表示智能体i的观测量，用o={o1，o2，…，oN}表示所有智能体的联合观测量；A={A1，A2，…，AN}为智能体的联合动作空间，其中Ai表示智能体i的动作空间，用ai∈Ai表示智能体i的动作，用a={a1，a2，…，aN}表示所有智能体联合动作；R={R1，R2，…，RN}为智能体奖励函数集合，其中Ri：S×A→R表示智能体i的奖励函数，所有智能体在环境状态s采用联合动作a后所获得的奖励用ri表示，其中ri=Ri(s，a)。可以看到智能体i的奖励不仅跟自身动作策略有关，还受到其他智能体策略的影响。状态转移概率P为指定智能体i在联合状态s及联合动作a时，环境状态改变到下一个环境状态s′的概率分布，可用P：S×A×S→[0，1]来表示，γ为累积奖励衰减因子。强化学习中多智能体与环境交互的过程如图3所示。

图3 强化学习多智能体与环境交互过程Fig.3 Reinforcement learning process of interaction between multi-agent and environment

定义智能体i的策略概率密度函数为

式中：μ为智能体策略网络；θi为智能体i的策略网络参数。

定义智能体i的累积奖励函数为

式中：π-i表示除智能体i以外其他所有智能体的联合策略。根据智能体之间奖励函数的不同，可以分为不同的场景任务，即若所有智能体奖励函数相同，目标一致，称为完全合作型；若智能体间奖励函数相反，通常为两方零和博弈，一方收益是另一方的损失，称为完全竞争型；若智能体间既有竞争，也有合作，多为一般博弈，称为混合关系型。

本文多无人机攻防对抗问题属于混合博弈，所有智能体学习的目标可以表述为

式中：π*i为智能体i的最优策略。

2.2 MADDPG算法

MADDPG算法［22］是一种经典的多智能体强化学习算法，采用“集中式训练、分布式执行”的方式，能够适用于环境不稳定的情况，可应用在合作、竞争及混合合作竞争的多智能体环境。假设有个N智能体，对于每个智能体均有各自独立的Actor策略网络和Critic评价网络，设定Actor当前网络和目标网络的参数分别为θ={θ1，θ2，…，θN}、θ′={θ′1，θ′2，…，θ′N}，Critic当前网络和目标网络的参数分别为w={w1，w2，…，wN}、w′={w′1，w′2，…，w′N}，由于每个智能体的Critic网络不仅输入自己的观测状态及动作信息，也包括其他智能体的状态及动作信息，因此对于MADDPG算法第i个智能体的Actor策略网络和Critic值函数网络输入输出关系如式（9）和式（10）：

每个智能体的Critic网络输入相同，MADDPG算法的网络结构设计如图4所示。

图4 智能体i的Actor和Critic网络Fig.4 Actor and Critic network of Agent i

从经验池D中随机抽取出m条训练样本，第j条训练样本为(oj，aj，rj，o′j)，其中和o′j=分别表示该条经验所有智能体的状态量、动作、奖励和下一刻的状态量。

定义MADDPG算法智能体i的Critic动作值函数的损失函数为J(wi)，它的梯度计算公式为

智能体i的策略梯度计算公式为

因此Critic当前网络参数w={w1，w2，…，wN}和目标网络参数w′={w′1，w′2，…，w′N}的更新公式可以表示为式（14）和式（15）：

Actor当前网络参数θ={θ1，θ2，…，θN}和目标网络参数θ′={θ′1，θ′2，…，θ′N}的更新公式可以表示为式（16）和式（17）：

式中：αC、αA、τ分别为Critic网络学习率、Actor网络学习率以及软更新参数。

2.3 PER-MATD3算法

TD3算法［23］将动作值函数进行解耦，使用2个Q网络来近似动作选择和动作评估，能够有效解决高估问题，在单智能体中相较DDPG算法一般表现出更好的效果。MADDPG算法是DDPG算法在多智能体领域的扩展，它并没有改变动作值函数高估问题固有的特性［24］，智能体i在策略评估及改善过程中依然存在以下高估误差：

借鉴TD3算法的实现过程，利用MADDPG算法中“集中式评判、分布式学习”的网络框架，提出MATD3算法。MATD3算法有以下几个特点：一是每个智能体不仅有各自的当前策略网络及对应的目标策略网络，还有2个中心化的独立评估网络及对应的目标网络，通过选择较小的Q值从而接近真实Q值以缓解高估问题；二是为了适用于环境不稳定的情况，采用中心训练分布执行的架构；三是使用策略延迟更新方式，即评估网络在更新一定步数之后再对策略网络进行更新。MATD3网络结构设计如图5所示。

图5 MATD3算法网络结构设计Fig.5 Design of MATD3 algorithm network structure

图5中，每个智能体i包括6个网络，分别为：当前策略网络μ(oi；θi)；目标策略网络μ(oi；θi′)；当前评估网络1：q(o，a；wi，1)；目标评估网络1：q(o，a；w′i，1)；当前评估网络2：q(o，a；wi，2)；目标评估网络2：q(o，a；w′i，2)。策略网络仍采用分布式执行方式，输入自身的状态信息，输出决策的动作；2个Critic网络采用集中式训练方式，不仅输入自身局部的状态和动作，还包括其他智能体的状态和动作信息，输出的是2个近似真值的Q值。在计算目标Q值时，为了缓解高估问题，同单智能体方式一样，选择较小的目标Q值来指导策略网络的参数更新。

经验回放机制［25］是在深度Q网络（DeepQNetwork， DQN）算法中首次提出的，在经验回放时候，不是简单地随机采样，而是依照每个样本的重要程度对其优先级排序，在抽样时能够更多次的访问重要程度较高的样本，从而能够有效的学习。而样本的重要程度可以利用时间差分法中的TD-error进行衡量，TD-error较大的样本被赋予较高的优先级，相反，TD-error较小的样本被赋予较低的优先级［26］。PER方法在单智能体领域表现出色，而在多智能体中依然是一个研究热点。因此本研究将PER方法扩展到多智能体领域中，并与前文的MATD3算法进行结合，提出了PER-MATD3算法。

TD-error为估计Q值与目标Q值的差。而在MATD3算法中，假设经验池D中第j个样本为(oj，aj，rj，o′j)，结合中心化训练和TD3方法中缓解过估计的问题，智能体i的目标Q值定义为

为了打破随机抽样准则，定义智能体i抽取第j个样本的概率为

式中：m为当前经验池中样本数为样本的优先级；α为一个0～1的数，用来控制随机采样和贪婪采样的调节系数。用和分别表示智能体i的第j个样本采用评估网络1和评估网络2的TD-error，则由和中的较大值决定。选择2个估计Q值与目标Q值差较大的值的绝对值作为TD-error，定义为

Q网络的学习过程就是不断减小每个智能体TD-error的过程。由于智能体在与环境的交互中不断存储新的数据，若在训练阶段每次都要对经验池的样本按照优先级从大到小的排序，是非常耗费计算时间的。可利用数据结构中的SumTree的树形结构，在叶子节点上存储每个样本的数据和优先级，而父节点只需存储2个分叉子节点优先级之和，因此树的根节点就是所有样本的优先级之和，采用这种数据结构可以使得时间复杂度变为Olog10n，大大简化计算过程。

由于在使用了优先经验回放方法时会有偏的带来样本分布的变化，因此还需加入重要性采样方法，这样既保证每个样本被选到的概率是不同的，从而加快训练速度，又可以使得在训练时每个样本在梯度下降时的影响是相同的，从而保证收敛的结果，重要性采样的权重定义为

式中：cji为智能体i对第j个样本的采样权重；m为当前经验池中的样本数；β为抵消优先经验回放方法对收敛结果的影响程度。

一般在程序中需要进行归一化处理，即将每个样本权重除以最大的权重，推导公式为

式中：k为样本权重最大的那个样本序号。因此相较之前的MATD3的Cirtic损失函数，现在考虑加入样本优先级的新的Critic1和Critic2的损失函数J(wi，1)和J(wi，2)分别为式（24）和式（25）：

式中：yji为式（19）中的目标Q值；q(oj，a；wi，1)和q(oj，a；wi，2)分别为Critic1和Critic2网络的估计Q值。

3 基于PER-MATD3算法的多无人机攻防对抗机动决策设计

3.1 状态空间

进攻无人机的状态信息包括无人机自身的位置、航向角、速度大小、无人机对障碍物及边界的探测信息和目标方向信息。为了使得进攻方更具智能性，进攻无人机能够通过激光雷达载荷探测到各架防守无人机位置，从而可提前规避。因此进攻无人机的状态空间总共包含11维数据，定义为

对于第n架防守无人机，状态信息除了自身的位置信息、航向角、速度大小、无人机对障碍物及边界的探测信息、进攻目标的方向信息以外，而且能够通过地面雷达实时了解到其他2架无人机与自身的距离信息，记为sdnm。因此每架防守无人机的状态信息变为13维数据，定义第n架防守无人机为

用代表防守无人机n与防守无人机m1的距离，在上式中dnm1的定义为

3.2 动作空间

动作空间表征为加速度和角速度，如式（29）所示：

3.3 奖励函数

为了解决稀疏奖励所带来的样本训练效率低下的问题，本实验中奖励函数采用引导型奖励和稀疏奖励相结合的方式。在无人机与环境交互过程中，如果碰撞边界、或者碰撞障碍物、或完成任务，则采用稀疏奖励；这3种情况均不发生的时候，采用引导型奖励。

设计引导型奖励Rg为

式中：α1、α2、α3、α4、α5为加权系数。

Rg的各种引导奖励的定义如式（31）所示：

式中：dt-1和dt为无人机上一时刻和当前时刻距离目标的相对距离；Rdis为无人机上一时刻和当前时刻与目标的相对距离的变化量；Rr为无人机的每个探测传感器状态量相对于1的值；Rv为无人机当前速度大小所带来的奖励量；Rc为无人机当前航向ψi与最优航向ψopti的偏差。

对于防守无人机，考虑加入防守无人机之间碰撞惩罚Rne，仅当防守无人机之间距离较近时才给予惩罚，定义为

设计稀疏奖励Rs的公式为

式中：R1为无人机碰撞战场边界的惩罚；Rko为第k种障碍物的半径；dis(·)为二维空间的欧式距离；R2为无人机碰撞障碍物的惩罚；Rt为目标区域的半径；Rf为防守无人机的火力打击距离；R3为无人机完成任务的奖励或任务失败的惩罚，对于进攻无人机到达目标区域则为任务成功，被防守无人机击毁为任务失败，对于防守无人机则相反。

3.4 训练算法设计流程

基于PER-MATD3的多无人机攻防对抗算法流程如算法1所示。

算法 1 基于PER-MATD3的多无人机攻防对抗机动决策算法1 2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.初始化每个无人机i的网络参数θi、wi，2和wi，2及对应目标网络参数，经验回放树SumTree的默认数据结构，其叶子节点的优先级pj设为1，批样本数m，调节系数α，采样权重系数β，衰减因子γ，评估网络相对策略网络更新频率C，软更新系数τ，高斯噪声σ For episode=1 to MaxEpisode do获取双方无人机各自的观测状态o1，1，o1，2，…，o1，N For t=1 to MaxStepdo For i=1 to N do对于无人机i，执行动作at，i=fclip(μ(ot，i；θi)+N)，其中fclip表示无人机的限制动作上下限的函数，得到对应的奖励值rt，i，及下一时刻的状态o(t+1)，i End For将样本数据{ot，1，ot，2，…，ot，N，at，1，at，2，…，at，N，rt，1，rt，2，…，rt，N，o(t+1)，1，o(t+1)，2，…，o(t+1)，N}存储到SumTree中If StartTrain do根据式（20）得到m数量样本数据(o，a，r，o′)，并根据公式（22）计算oi，j For i=1 to N do根据式（24）和式（25）计算J(wi，1)和J(wi，2)根据式（20）和式（21）更新样本的优先级更新参数wi，1和wi，2每隔C步根据式（13）计算▽θiJ(θi)，根据式（16）更新参数θi根据式（15）和式（17）更新参数w′i，1，w′i，2和θ′i End For End If End For End For

4 仿真实验

4.1 实验环境及参数设置

实验的软件采用Pycharm 2020.1和Anaconda3平台，实验的程序是基于Python语言，针对设定的对抗场景如图1，采用python标准的GUI编写库Tkinter构建二维战场环境，神经网络的构建采用Pytorch模块，版本为1.3.1。

本次实验将利用多智能体强化学习算法研究多无人机攻防对抗场景的问题，首先需要构建仿真环境，环境初始化具体参数设置如表1。

本实验分别采用基于模仿学习的深度确定性策略梯度算法（Imitation Learning based Deep Deterministic Policy Gradient algorithm，ILDDPG）［27］、MADDPG算法、MATD3算法及改进的PER-MATD3算法对上述构建的多机攻防对抗场景智能决策问题展开研究，由于4种算法均采用分布式执行的设计框架，因此各个算法针对智能体i的Actor网络均设计为图6的网络结构。

图6 智能体i的Actor网络结构Fig.6 Actor network structure of Agent i

而各个算法具体的Critic网络结构设计如表2所示。Critic网络的激活函数均采用Relu函数，并采用Adma优化算法进行反向传播更新网络的参数，算法的超参数设置如表3所示。将智能体与环境交互产生的数据样本存入经验池中，本文设定一旦样本数量达到经验池容量一半后才开始训练。对于MATD3和PER-MATD3算法，设置的策略延迟更新频率系数为10，而对于PER-MATD3算法，式（20）和式（22）的参数α和β分别为0.6和0.5。

表2 智能体i的Critic网络结构Table 2 Critic network structure of Agent i

表3 超参数设置Table 3 Hyperparameter settings

4.2 训练过程

强化学习算法的目的是训练智能体的策略使得它的累积奖励的期望达到最大，训练结果的评价指标一般可用回合的平均奖励值来衡量。回合的平均奖励值是智能体最近回合所得奖励的平均值，它是智能体训练所得的奖励值随回合变化的曲线图，奖励值上升越快，奖励值收敛时越平稳且越高，则证明训练的效果越好［28］。在本实验中使用最近100回合的平均奖励作为最终的回合平均奖励值，若在开始训练时不够100回合就仅使用已有回合的平均奖励值。针对图1构建的多无人机攻防对抗场景的机动决策问题，分别利用上述四种不同的多智能体强化学习算法进行训练，等待无人机训练2 000回合的过程完成，分别将4种算法所有无人机平均奖励总和曲线绘制在同一个坐标轴内，如图7所示。

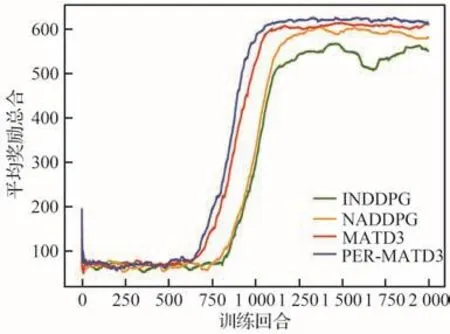
图7 4种算法的平均奖励Fig.7 Average reward of four algorithms

在图7中，横坐标代表训练的回合数，纵坐标代表4架无人机在最近100回合内平均奖励的总和。在起始阶段，4种算法均是无人机与环境交互产生训练样本的过程，回合奖励很低，无人机并不清楚自身要做什么。在样本数达到经验池容量一半时开始进行训练，随着回合奖励曲线逐渐上升，各架无人机逐渐开始学习到更为智能的策略，并都最终达到了收敛的结果，但是相比之下4种算法在性能表现上有所差异。经过比较，可以得到4种算法中PER-MATD3算法收敛的速度最快，在收敛后的平均奖励最高，同时，PER-MATD3和MATD3算法在收敛后均保持有较好的稳定性能，ILDDPG算法的稳定性很差，这是由于智能体所观测环境具有不稳定性造成的。

表4 4种算法训练过程数据对比Table 4 Comparison of four algorithm training process data

将4种算法训练过程的重要参考数据进行统计分析，这些数据有利于直接表现各个算法的性能优劣。主要包括开始训练的回合数、在1 000回合时的奖励值、1 000～2 000回合的平均奖励值、训练时奖励所达到的峰值。表4结合图7对以上指标参数进行统计分析。

从表4中可以得到，PER-MATD3算法在训练阶段其训练速度非常快，可从1 000回合的奖励值来得到；在达到收敛后的奖励结果较高，稳定性也较好，表现更好的性能优势，验证所提出的PERMATD3算法相较其他多智能体算法的有效性。

4.3 测试结果

为了研究4种算法在收敛后的表现，进一步验证基于PER-MATD3算法的多机攻防对抗机动决策的优势，可利用4种算法在2 000回合收敛后的网络参数进行对抗测试分析，将进行对抗结果测试分析，利用训练好的网络进行10 000次蒙特卡洛实验，具体方法是将2 000回合的一架进攻无人机和3架防守无人机的Actor当前网络参数单独拿出来，作为生成无人机动作的网络参数。根据环境的初始设置输入各架无人机所观测环境的状态量，利用动作网络生成决策动作，与环境进行交互。

一次回合终止条件具体分为2种，一种是无人机与环境交互的时间达到每回合设置的最大时间。另外一种是回合提前结束，其中，防守失败包括3种情况：① 防守无人机碰撞边界，此时奖励函数采用稀疏奖励，对应式（33）中稀疏奖励Rs=R1；② 防守无人机碰撞障碍物，此时奖励函数采用稀疏奖励，对应式（33）中稀疏奖励Rs=R2；③ 进攻无人机成功完成任务，即防守失败，对防守无人机来说，式（33）中Rs=R3，这时的R3是一个惩罚项，取负值。防守成功时，防守无人机击毁进攻无人机，这时的R3是一个奖励，取正值。

将4种算法在双方无人机上的表现进行分析，这里仅站在防守方角度来对成功、失败及其他情况进行统计，而进攻方的结果刚好与其相反。双方对抗结果情况如图8所示，其中绿线表示防守方的失败次数、红线表示防守方的成功次数，蓝线表示其他情况的次数，即无人机碰撞边界或障碍物的次数。

图8 双方对抗结果统计Fig.8 Statistics of results of confrontation between two sides

通过柱状图8，可以得到以下结论：首先，统计结果表明，通过设计的4种不同算法所训练的双方无人机，无论是在避免碰撞边界或障碍物方面还是在完成自身规定任务方面的表现，均具有一定的智能性，在图中可看出其他情况的次数相对非常少；其次，在同一张柱状图内，进攻方采用的是之前训练2 000回合的同一种算法的策略网络，而防守方分别采用4种不同的算法，相比之下PER-MATD3算法相较其他3种算法能够使得防守方获得更高的成功率，而ILDDPG算法在训练期间评估网络并没有观测到全局状态信息，因此其策略网络使得防守方的训练效果表现最差；最后，在不同的柱状图之间，进攻方采用PERMATD3算法同样也比其他3种算法具有更高的成功率，进一步验证所提出的PER-MATD3算法具有更好的性能。

由于4种算法所训练的环境一样，将PERMATD3算法进行测试，最终仿真对抗的测试效果图如图9所示。

图9 PER-MATD3算法训练效果测试Fig.9 Test of training effect of PER-MATD3 algorithm

5 结论

本文主要围绕多无人机攻防对抗问题进行了具体研究，建立1对3的环境模型，然后介绍了多智能体强化学习算法的理论推导与设计过程，具体包括MADDPG算法及MATD3算法，并在此基础上详细介绍了基于优先经验回放机制所设计的PER-MATD3算法，将算法与问题相结合使得无人机在环境交互中进行学习。最终仿真实验结果表明，多智能体强化学习算法在多无人机攻防对抗问题上有不错的效果，并且通过4种算法在攻防双方上应用时横向及纵向的实验对比，验证所提出的PER-MATD3算法相较其他3种算法具有更好的训练表现。

后面可尝试将本文的算法应用在三维场景的多机攻防对抗问题中，并考虑双方不同机动参数对对抗结果的影响。