基于超声能量衰减的螺栓轴向应力测量

陈平，叶霞，刘华强，胡义亮，余鑫

重庆大学 机械与运载工程学院，重庆 400044

航空结构中包含许多精密的螺栓连接件，螺栓轴向应力过大会增加螺栓负荷，严重时导致螺栓断裂。轴向应力过小容易导致联接不可靠，甚至结构的局部解体［1］。实现螺栓轴向应力精确测量对预防螺栓联接失效具有重大意义，控制螺栓轴向应力大小是提高航空结构连接质量、降低航空事故发生率的重要措施［2］。由于航空结构具有高温、高速、高振动的特点，需要加强对航空结构中螺栓轴向应力的精确测量，提高其安全性、稳定性。目前常见的螺栓应力测量手段包括扭矩扳手法［3］、电阻应变片法［4］、X射线衍射法、光测力学法、垫片式压力传感器法、超声检测法。超声检测法是目前应用最为广泛且较为成熟的一种通用型无损检测方法［5-10］，具有测量精度高、检测速度快、操作便捷等优势，非常适用于精确测量航空紧固件的应力。

超声检测法的基本原理是声弹性效应，即静应力状态下固体结构中的弹性波相速度会随应力幅值发生变化。由于声速难以直接获取，实际操作中一般测量的是超声在固体中传播的时间，即渡越时间。潘勤学等［11］基于声弹性效应，提出在单波脉冲反射实验中使用不同应力状态下的渡越时间差来测量已安装螺栓的应力。Yasui和Kawashima［12］发现使用纵横波渡越时间比值可测得已紧固螺栓的应力。以上是目前应用最为广泛的2种螺栓轴向应力超声测量方法，其精度和可靠性可基本满足一般工程应用。然而，当用渡越时间来评估航空螺栓轴向应力时，难以达到理想的效果。超声在受载螺栓中渡越时间的增长包括2大因素，一是螺栓拉伸后导致的声程增加，二是声弹性效应造成的声速变慢。航空螺栓强度大，在载荷一定时其伸长量相对较小，故其渡越时间变化基本由声弹性效应造成。由于声弹性效应非常微弱，其造成的渡越时间增量也非常小。在这种情况下，只能使用采样频率极高的仪器才能获取准确的渡越时间。由此可见，渡越时间法难以满足高强度螺栓应力测量的要求。

近年来有研究指出，在受载固体中除弹性波相速度外，其衰减系数同样会随应力状态改变。Kube等［13-15］基于多晶体微观层面上的本构关系提出了包含柯西应力的等效弹性常数。Arguelles和Kube［16］基于上述研究以及Weaver［17］的散射衰减系数模型，提出了考虑应力影响的散射衰减系数。与声速相比，散射衰减系数的取值主要与内部各向异性有关，而对螺栓的规格、材质以及安装情况等因素不敏感。本文基于超声波散射衰减原理，提出使用超声能量衰减进行螺栓轴向应力测量。分析了频散现象对衰减系数测量的不利影响，并针对性地提出使用多次回波频谱能量比测量应力。通过实验，证明了该方法在测量航空螺栓应力时可达到较渡越时间法更高的精度。

1 理论模型

超声在传播过程中发生的能量损耗称为超声衰减，按原理可分为耗散衰减、吸收衰减和散射衰减［18］。耗散衰减是指在无界空间中，声束截面积随传播距离增长而导致的波前声强发散。然而，金属杆边界的反射效应会使得耗散衰减大大降低。吸收衰减是指超声在黏弹性材料中传播时，声场中各点振动时克服黏滞力所引起的热损耗。当超声在螺栓等金属杆类零件中传播时，由于介质不具有黏弹性，故基本不存在吸收衰减。散射衰减是指相干声束在通过介质中声阻抗不匹配界面时产生的扰动所带来的能量损耗，超声在螺栓中的衰减主要由散射产生。

当弹性波在无织构多晶体材料中传播时，介质本身的应力状态会对弹性波的相速度以及内部散射衰减系数产生影响，该现象可定义为多晶体的声弹性效应。在平均晶粒直径为l的介质中的衰减系数αL→S有如下关系式［16］

式中：L为纵波；S为横波；ω为中心频率；ρ为密度；VL为入射波相速度；VS为散射波相速度；θ为入射波与散射波传播方向的夹角；ΓL→S为散射状态矩阵。h和g具体表达式为

其中：σ代表柯西应力的幅值。

此外，横波按偏振方向可分为SH波和SV波，散射的同时会产生模式转换［16］，当入射波为L波时，其散射过程包含L→L，L→SH，以及L→SV。ΓL→S按照散射过程可分为3种情况，其具体表达式为

式中：ν为二阶各向异性常数；ζ为综合各向异性常数。

为简化问题，假设多晶体材料中各个晶粒具有相同的弹性性质，但其取向随机，故需对散射角在各个方向上进行积分。式（1）中的相速度V实际上同样会随应力状态发生改变，但由于相速度随应力的改变率非常小，故在式（3）中可将相速度视为常数。当(ωl)2/V2≪1时，即属于瑞利散射区时，纵波衰减系数可近似表示为

同理，横波衰减系数可表示

由式（4）、式（5）可知，超声波发生瑞利散射时，在立方对称多晶材料中传播时的纵波和横波衰减系数与应力呈二次的关系。

2 基于超声能量衰减的螺栓轴向应力估计模型

为简化问题，将整个螺栓等效成应力均匀分布的圆柱体，定义L0为该圆柱体的长度，LC称为夹紧长度，如图1所示。设均匀化后的拉应力幅值为σ，其衰减系数为α(σ)，而零应力轴段的衰减系数为α(0)。整个螺栓的纵波平均衰减系数可表示为

图1 螺栓受力图Fig.1 Bolt stress diagram

将式（4）代入式（6）得

衰减系数还可表示为［19］

其中：S1(f)和S2(f)分别对应信号一次回波和二次回波频谱的幅值，f为截止频率；L代表声程，即螺栓全长L0。

然而按照多晶体超声统一散射理论［20］，在散射体相干长度一定时，归一化波数越小（即频率越高），超声散射方向的随机性及其强度也就越大。因此，当频率较高时，信号中一次回波和二次回波的相干性会明显变差。此外，当超声从螺栓端面入射并进入其内部后会在边界发生一系列反射和模式转换［21］，由此衍生出的波束互相干涉，最终可激发出由多个模态叠加而成的纵向柱面导波［22］。由于这些模态的中心频率和群速度不同，柱面导波信号在时域和频域上均包含多个波峰，且这些波峰彼此之间存在严重干扰。图2～图4为实际测量螺栓应力时得到的纵波、横波时域信号及对应的一次和二次底面回波频谱。从图中可看出，信号一次和二次底面回波的频谱差别较大且非常杂乱，此时明显无法利用式（9）计算衰减系数。

图2 纵波、横波时域信号Fig.2 Longitudinal wave signal and shear wave signal

图3 纵波信号一次和二次回波频谱Fig.3 Primary and secondary echo spectrum of longitudinal wave signal

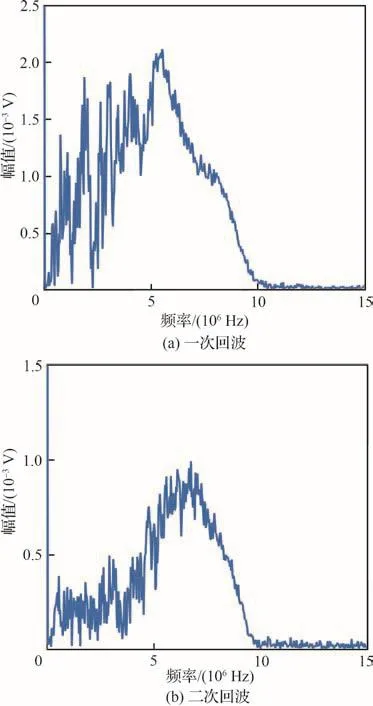
图4 横波信号一次和二次回波频谱Fig.4 Primary and secondary echo spectrum of shear wave signal

虽然超声的散射以及模态混叠会导致声场相干性变差，但由于螺栓属于有界介质，当采集时间足够长时，大部分声场能量最终均会回到端面并被换能器接收。因此，使用一次和二次回波信号能量比值代替衰减系数计算轴向应力，将这种方法定义为能量衰减法。根据帕斯瓦尔定理，超声能量可表示为

式中：fmax和fmin表示信号的高、低截止频率。对式（9）两边分别取反对数

因此，一次回波S1(f)的频谱能量E1可以写成

式（12）按照泰勒公式展开，可近似为

由式（10）、式（13），纵波一次和二次回波的频谱能量可分别表示为

纵波一次和二次回波频谱能量比值可写为

结合式（7），R(σ)可由AL、BL、CL、XL等螺栓声学参数、材料参数表示为

将螺栓材料设定为高强度45钢，其密度为7 890 kg/m3，纵波速度为5 890 m/s，横波速度为3 230 m/s。45钢的二阶各向异性常数取-139 GPa，综合各向异性常数取-0.043 9 GPa-1，β取值为0.5～0.9， 晶粒直径取50 μm，螺栓的全长55 mm。设定超声信号类型为高斯型脉冲，其中心频率为10 MHz，上下截止频率分别为6 MHz和18 MHz。由于轴向应力的可能范围为0～200 MPa，则由以上条件可以计算出ALσ2/(BLσ)的数量级为10-3。因此，式（16）可以表示为

R(σ)是由BL和CL组成且与应力相关的线性函数，由于ζ对所有金属材料均为负值，因此R(σ)与σ呈线性递增关系，式（18）可以直接应用于拟合实验中获得的能量比曲线。此外，式（18）还表明R(σ)的斜率与几何夹紧长度LC有关，因此必须考虑LC对测量结果的影响。

同理，横波信号能量比值可表示为

3 螺栓应力测量实验

3.1 实验系统

实验系统如图5所示，信号源采用美国JSR Ultrasonic公司生产的PRC50脉冲发射板卡，其最大激励电压475 V。该发射卡集成了前置放大器，增益范围为-14～60 dB。数据采集使用台湾凌华公司生产的AD-Link PCIE9852采集卡，其最大采样频率200 MHz，AD转换位数14位。将以上硬件集成于工控机中，并使用LabView完成DAQ系统搭建。该工控机可以通过RS232串口控制拉伸试验机（上海协强仪器制造有限公司，CTM2200S）并读取其配套压力传感器数据。超声探头采用日本Olympus公司生产的接触式单晶纵波探头A112S-RM、横波探头V156-RM，2种探头的中心频率分别为10 MHz、5 MHz，晶片直径均为6 mm，测量时分别使用纵波探头专用耦合剂B2、横波探头专业耦合剂SWC-2。选取2种不同规格螺栓作为试验对象，其详细参数如表1所示。

表1 螺栓试件参数Table 1 Bolt specimen parameters

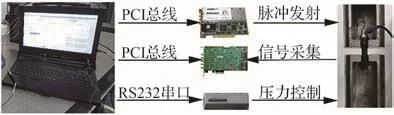
图5 实验系统组成Fig.5 Composition of experimental system

3.2 螺栓参数标定实验

首先使用拉伸试验机对试件进行加载，加载范围为0～200 MPa，步长为10 MPa。为减少频谱泄漏对测量结果的影响，在进行傅里叶变换前先对信号一次和二次回波时域信号加汉明窗。实验试件能量衰减随应力变化曲线如图6、图7所示。显然，曲线变化趋势与理论分析结果基本一致，能量衰减系数与应力近似呈线性递增关系。故标定时可使用以下模型：

图6 试件A能量衰减曲线Fig.6 Energy attenuation curves of specimen A

图7 试件B能量衰减曲线Fig.7 Energy attenuation curves of specimen B

式（21）中的未知参数K、b可通过对标定数据进行线性拟合获得，拟合结果如表2所示。

表2 标定曲线拟合结果Table 2 Calibration curve fitting results

图8、图9分别为试件在加载过程中一次回波的声时差。声时差定义为受载情况下与未受载情况下，信号一次回波包络信号的峰值坐标之差。从图中可看出声时差随应力呈一次线性递增，但图中的所有曲线均发生了明显的阶梯状畸变。这是因为螺栓刚度过大，且渡越时间的变化量小于采样周期，故无法得到其精确值。由于横波声弹性常数小于纵波声弹性常数，横波的应力-声时差曲线的畸变相对更严重。以上现象说明，当螺栓的强度较大且采集硬件的采样频率有限时，传统的单波声时差法的测量精度会下降。本文提出的能量衰减法则基本不受以上条件影响。

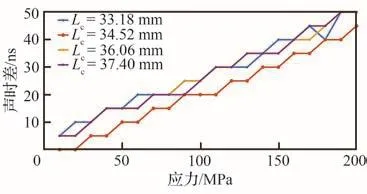
图8 试件B纵波应力-声时差曲线Fig.8 Longitudinal wave stress acoustic time difference curves of specimen B

图9 试件B横波应力-声时差曲线Fig.9 Shear wave stress acoustic time difference curves of specimen B

3.3 螺栓应力测量实验

根据3.2节参数标定结果分别采用能量衰减法与声时差法测量对应螺栓轴向应力，其中加载范围为0～200 MPa，步长为10 MPa，测量结果分别如图10、图11所示。对比分析测量结果可知，不同应力下能量衰减法测量误差均小于7%，而因螺栓强度较大造成声时变化量微小，且硬件采样频率不够导致声时差法测量误差波动较大，最大误差超过15%，其测量精度远低于能量衰减法。因此超声能量衰减法较传统的声时差法更适合高强度螺栓应力的测量。

图10 能量衰减法测量结果Fig.10 Measurement results of energy attenuation method

图11 声时差法测量结果Fig.11 Measurement results of acoustic time difference method

4 结 论

本文基于宏观各向异性多晶体的散射衰减规律，提出以超声回波频谱能量衰减率测量螺栓轴向应力。推导了理论模型并搭建了螺栓轴向应力测量平台。结合实验结果，可得以下结论：

1） 根据理论模型，超声能量衰减系数与螺栓轴向应力呈线性递增关系，并简化了螺栓材料参数的标定模型。

2） 对比应力测量实验结果，能量衰减方法在测量航空螺栓时误差率小于7%，相对现存的基于渡越时间的声时差法具有较高的灵敏度及分辨率。

3） 在实验中发现，探头耦合情况对测量精度有较大影响。未来将继续研究超声探头耦合情况对能量衰减的影响，进一步提高测量精度及耦合稳定性。