补偿函数观测器及其在飞行器姿态控制中的应用
赵旭,齐国元,*,蔚昕晨,胡建兵,李霞
1.天津工业大学 控制科学与工程学院,天津 300387
2.天津工业大学 机械工程学院,天津 300387
四旋翼飞行器具有机动性强、体积小、自主执行任务的能力强等优点。随着计算机处理能力的提高及传感器和执行器成本的降低,该飞行器被广泛应用于军事和民用等领域[1-3]。由于四旋翼飞行器系统的欠驱动、非线性等特性,其姿态控制容易受到四旋翼数学模型中的非线性项、外部扰动项和未建模动态及负载的影响,这些因素极大地破坏了四旋翼飞行器系统的稳定性和控制品质,甚至会使系统出现混沌振荡行为[4-5],因此四旋翼飞行器抗干扰能力成为影响其姿态控制精度的主要因素。
在实际的工程中,由于未建模部分的动力学特性和外界不确定因素的影响,很难获得四旋翼飞行器精确的数学模型,这在很大程度上限制了依赖于模型控制算法的实际应用。当这种模型不确定性以及外部未知扰动作用变强时,依赖模型控制器的参数整定变得更困难,这进一步加大了这类控制器的应用难度。因此,不依赖模型的控制方法在工程上获得广泛应用。
不依赖模型控制是基于通过输入—输出行为信息不断更新估计系统模型函数的一种控制方法[6-7]。这种方法的关键特征在于,模型观测器在线估计模型值或模型偏差和扰动值总和,控制器在线前馈应用估计所得到的系统未知函数值和扰动。因此,即使被控系统具有高度非线性、时变、耦合、外扰动,这些信息通过观测器估计能在控制器中得到部分补偿。
PID 控制是典型的不依赖模型的控制方法,如Salih 等[8]将PID 用于四旋翼3D 空间的飞行,但PID 没有在线估计未知模型函数值或扰动值的能力,因而不能实现在线补偿,而只是依靠误差的整定,随着扰动增大,控制品质可能变差。随着智能理论的发展,研究者们提出了结合智能理论的新型PID 控制器,如专家系统PID 控制器[9]、模糊PID 控制器[10]、神经网络PID 控制器[11]等,并被相继应用于四旋翼的控制。系统模型值和扰动值称为总扰动[12],而扩张状态观测器(Extended State Observer, ESO)能够有效的估计总扰动,所以Han[13]提出了自抗扰控制(Active Disturbance Rejection Control,ADRC)。ADRC 可以基于系统误差,设计控制器参数,同时,在线应用该估计值,实现不依赖模型控制。这种方法的一个关键特征是通过对干扰或模型不确定性的处理、提高了系统控制的鲁棒性和自适应能力。Dong 等[14]将ADRC应用于多旋翼飞行器位置控制。除此之外,ADRC 在姿态控制中也有应用[15],李霞和陈奕梅[16]采用降阶ADRC 控制四旋翼位置和姿态,在满足系统稳态性能和动态性能的前提下,降低了系统带宽与噪声的敏感度。Zhao 和Guo[17]针对具有动态和外部不确定性的SISO 非线性系统,设计了非线性自抗扰控制器并给出了变量收敛性的严格证明。Gao[18-19]对自抗扰控制中的主要模块进行了线性化处理,并引入了带宽的概念,提出了线性自抗扰控制(Linear Active Disturbance Rejection Control, LADRC),并在实际的无人机控制中得到了应用[2,20]。然而,Qi 等[21-22]研究发现,ESO 的估计精度不高,对快速机动变化的模型函数或扰动不能实现估计收敛。ESO 的结构导致了ESO 仅可等效为I型跟踪系统,只能对常量模型函数实现无差估计[21],而飞行器系统的动力学模型和扰动是动态变化的,这些未知模型函数或扰动信号的泰勒展开中的一次项、二次项甚至三次项会主导函数变化,因此造成ESO 估计精度较低。因此,Qi 等[21]提出了补偿函数观测器(Compensation Function Observer, CFO),采用信号跟踪思想进行设计结构,采用积分串级结构,应用速度误差信息,采用一阶滤波器或积分器作为未知函数或扰动的补偿,使得CFO 的类型为Ⅲ型,能对常量、斜坡和加速度函数实现无差估计。
然而,对于飞行器处于强非线性干扰的环境下(如有强风干扰时),CFO 中的补偿器中的线性一阶滤波器不能充分逼近。有必要用非线性函数替代线性的一阶滤波器或积分项,以进一步提高估计精度,因此笔者提出用光滑的径向基(Radial Basis Function, RBF)神经网络的非线性拟合补偿函数替代CFO 中的线性一阶积分补偿函数。本文仍然采用CFO 的观测器结构,创新贡献在于:
1)提出带有RBF 神经网络的补偿函数观测器,使用RBF 神经网络替代原有CFO 中的一阶滤波器,实现补偿。因为RBF 神经网络能实现对非线性函数的逼近效果更好,因此将CFO 的线性函数补偿替换为非线性函数补偿。
2)针对具有未知扰动和不确定性的四旋翼飞行器姿态系统设计了不依赖模型控制策略。应用带有RBF 神经网络的补偿函数观测器估计未知模型函数,设计了模型补偿控制器。应用Lyapunov 稳定性理论,证明了所设计的带有RBF 神经网络的补偿函数观测器的控制闭环系统稳定性。
3)通过基于Pixhawk 的四旋翼飞行器姿态系统控制测试平台,实验验证了所设计的基于新的观测器的不依赖模型控制策略对不同参考姿态角的跟踪性能以及2 种控制器的抗扰性能。同时设计了自抗扰控制器,并与所提出的闭环控制策略进行了性能对比分析,进一步验证了所提出的带有RBF 神经网络的补偿函数观测器的模型补偿在控制性能上更具优势。
本文章节安排为:第1 节分析了补偿函数观测器优越于扩张观测器的结构和特点,指出存在的问题;第2 节提出了带有RBF 神经网络的补偿函数观测器,给出了收敛性分析;第3 节给出了四旋翼飞行器的模型和参数;第4 节提出了基于CFO 的模型补偿控制,并给出了稳定性证明,构建了各个通道的串级控制器;第5 节仿真分析;第6 节实验验证了模型补偿控制性能和抗干扰性能;第7 节总结本文的研究结果。
1 补偿函数观测器
针对单输入单输出(Single-Input Single-Output, SISO)二阶控制系统,设计函数观测器在线实时估计未知函数。
式中:y和为系统的输出;d为时变未知扰动项;为模型项;b为系统结构参数;u为系统输入。
假设 1令,假定为未知时变光滑非线性函数。
CFO 借鉴了ESO,其思想也包含Luenberger 观测器和齐国元等[22]所提出的高阶微分器、高阶微分反馈控制[7]、跟踪和型别思想,提出了模型补偿来解决模型函数估计精度问题和收敛性问题。下面首先分析一下补偿函数观测器思想和结构。完整的CFO 设计见文献[21],这里做一个分析性研究。
针对式(2)的系统模型,设计Luenberger 观测器为

图1 Luenberger 观测器Fig. 1 Luenberger observer
系统估计值与误差之间的等效开环传递函数为
则该观测器为Ⅱ型系统,这与该观测器2 个纯积分环节相对应。在后面的将详细给出类型的分析。
评注1观测器式(3)优势在于:①利用了位置和速度双重信息,速度信息比位置信息更接近加速度信息,而加速度信息直接关联未知函数,因此速度信息的使用大大提高了估计精度;②原系统具有纯积分(或称纯导数)结构,=x2,因此,该观测器保持了原系统的纯积分形式,即=z2,较ESO相比,纯积分环节能提高一个跟踪类型。
Zhu 等[23]在设计ESO 中包含了扰动估计项,其中扰动估计器中包含了系统的速度信息。这是一个间接使用速度信息方法,不是在ESO 中直接使用该信息。要使用速度信息,必须大幅度改变原来ESO 的结构,否则就不能保证稳定性。本文中的CFO 的结构采用的是Luenberger 结构,既能保证系统的稳定性,又能保证位置和速度信息的双重使用。
通过仿真发现,观测器式(3)估计精度高于ESO[21]。由式(2)减去式(3)可得Luenberger 观测器的观测误差为
式中:f为式(2)中的未知时变光滑非线性函数,显然,估计误差受未知函数f影响。
为了降低f的影响,改进观测器(3)为
基于观测器式(6)的估计误差为
为了解决该问题,考虑二者都用来逼近f,可以用一阶滤波器建立连接,即
在此基础上,Qi 和Chen[21]提出了可用带有滤波器的补偿函数观测器(CFO)来估计未知函数f,表达为
式中:λ为滤波因子。
评注2CFO 中补偿函数的引入,能一定程度上抵消模型函数未知问题,进一步提高估计精度。文献[21]的误差分析表明,补偿函数提高了观测器的1 个型别,加上纯积分结构增加的型别,该CFO 较ESO 提高了2 个型别,为Ⅲ型系统,因此大大提高了估计精度。
由式(8)和式(9)中的第3 个方程,有
可以得到
那么可以得出带有积分补偿形式的CFO,即
式(12)中的CFO也是三阶系统,与ESO有相同的阶次,其中z3通过积分补偿了原系统中的f。
图2 为带有积分补偿形式的CFO 原理框图,其开环特征方程为

图2 补偿函数观测器Fig. 2 Compensation function observer
通常,为了简化参数选取,同时保证CFO 稳定,令
式中:ω>0、-ω、 -4ω和 -4ω是CFO 的极点。从而有
其中:ωc是唯一的可调参数。
在CFO 设计中,对未知函数估计采用了控制中信号跟踪思想,如图3 所示,把这个观测器等效看成一个单位负反馈系统,观测器输入信号为未知函数f,输出为,传递函数G(s)的类型决定估计误差类型,类型不同误差有质的区别。

图3 观测器到跟踪器的转换Fig. 3 Transformation of observer to tracker
ESO 的结构如图4 所示,能够得到,其估计与误差之间的等效开环传递函数为

图4 ESO 结构框图Fig. 4 Schematic diagram of ESO
因此ESO 为I 型估计系统。
评注3CFO 为III 型估计系统,ESO 为I 型估计系统。在对未知函数或信号估计误差类型上有本质上差别。CFO 在收敛性方面能对常值、斜坡和抛物线函数实现零差估计,而ESO 是I 型系统,只能对常值函数实现零差估计,或导数有界函数[24-25],如对斜坡函数估计,误差有界,对抛物线函数估计误差发散,对一般的信号,如正弦信号等有较大的估计滞后。CFO 对斜坡和抛物线这样导数无界,甚至二阶导数无界函数都能实现估计收敛,对正弦函数估计误差也很小[21]。另外,CFO 通过结构解决精度和收敛性问题,不是通过参数调整,避免了因参数过大,恶化信噪比问题,而ESO 通过参数带宽调整精度,容易带来噪声放大。
评注4由系统式(1),f的估计等价于ÿ的估计,CFO的本质在于,它用ÿ̂位置y和速度信息估计了加速度信息ÿ,即ẏ获得了,那么就有f̂=ÿ̂-bu。一个系统通过IMU 等机载传感器能够获得位置y和速度ẏ信息,他们的变化能够反映系统受力或加速度信息,也就反映了f(y,ẏ,t,d)+bu信息,CFO 利用了速度信息,对于估计加速度信息更为可靠。
2 带有RBF 神经网络的补偿函数观测器
CFO 和ESO 都是基于系统已知状态,估计系统为未知函数,将未知函数当作信号或状态来进行估计,是观测扩张状态的思想。不依赖于系统模型或模型结构等特征。CFO 的补偿实现为式(8)或式(11),采用了一阶滤波器或积分器实现,λ值越高,补偿越充分,但由于λ是个参数,不宜太大。但采用高阶滤波会增加阶次和CFO 的复杂性。下面分析采用非线性函数替换的必要性。在实际中一个光滑的信号或函数可以表达成泰勒展开式为
由于采样时间τ≪1,特别高的高次项可以忽略,但是无论未知模型函数或信号f,往往不是简单的线性函数或信号,而是复杂的非线性形式(例如无人机中包含二次型函数、余弦函数;环境中的大风或阵风或紊流风所产生的风扰未建模动态,陀螺力矩、机体部分坏损、负载和气动阻力以及可能存在的内部或外部未知时变扰动),对于这些非线性较强的情况,泰勒展开中二次项、三次项不可忽略。尽管CFO 精度很高,但对泰勒展开中三次或四次仍然会带来误差。本文在针对正弦函数以及Duffing 方程的观测中发现,CFO 对这类非线性函数的估计仍有一定的误差。
因此本文采用RBF 神经网络替换式(12)的积分式,实现在线自适应更新权重,如同参数自适应控制方法[26],因而不涉及训练,另外,通常RBF 神经网络隐含层只含有5 个节点,其权值用一个自适应积分函数即可更新,不会大幅增加计算量。其重要意义在于利用了RBF 神经网络的非线性和光滑性,即使未知函数中包含泰勒展开的高阶次,快速变化的函数,RBF 神经网络也够充分地逼近。因此考虑使用RBF 神经网络这种非线性逼近高次项的方式,替换CFO 中的线性补偿结构,从而进一步提高估计精度。
设计RBF 神经网络为
式中:误差向量e作为神经网络的输入向量;h是高斯函数的输出,h=[h1,h2,…,hi,…,hn]T;i为隐藏层节点个数;ci为神经网络第i个节点的均值;W*是理想的神经网络权重;ε是神经网络的近似误差ε≤εN。
RBF 神经网络的实际输出,即补偿函数输出为
提出带有RBF 神经网络的补偿函数观测器,其表达式为
式中:γ>0,为调节因子;σ为滑模面函数,σ=Fe=l2e1+e2;F为滑模面函数的系数,F=[l2, 1]。式(21)中第3 个方程为RBF 神经网络自适应权重调节律。注意到带有RBF 神经网络的CFO 仍然是三阶系统,其框图结构如图5 所示。为了方便,记带有RBF 神经网络的CFO 为R-CFO。

图5 带有RBF 神经网络的补偿函数观测器Fig. 5 Compensated function observer with RBF neural network
定理1对于系统式(1),所提出的带有RBF神经网络的补偿函数观测器对未知函数f的估计能任意逼近,即
证明式(2)减去式(21)得
设计滑模面函数为
对σ求导得
定义李雅普诺夫函数为
对V求导,得
权重调节的自适应律为
则有
由于RBF 神经网络能实现任意逼近,误差ε足够小,可以获得。证毕。
3 四旋翼飞行器的动力学和运动学模型
本文所使用的四旋翼飞行器结构如图6 所示,该四旋翼为“×”型结构。通过控制1、3 和2、4 号电机的转速差实现四旋翼无人机俯仰角的控制,2、3和1、4 号电机的转速差实现无人机横滚角的控制,1、2和3、4号电机的转速差实现偏航角的控制。

图6 四旋翼飞行器Fig. 6 Four-rotor flight vehicle
如图6 所示,机体坐标系B={xb,yb,zb},大地坐标系E={x,y,z}。 其中:Fi(t),i=1, 2, 3, 4 代表4 个电机所产生的推力,推力方向为zb轴的负方向;θ、ϕ和ψ分别为四旋翼的俯仰角、横滚角以及偏航角,且有,
式中:Ωi为第i号电机的转速;kT为推力因子。
根据Newton-Euler 法,得到四旋翼动力学方程为
式中:m为四旋翼的质量;g为重力加速度;P为四旋翼的位置向量,P=[x,y,z]Τ;v为四旋翼整体的速度;e3为单位向量,e3=[0,0,1]T;̇表示四旋翼在大地坐标系E={x,y,z}中的角速度,̇=;ω表示四旋翼在机体坐标系B={xb,yb,zb}中的角速度,ω=[p,q,r]Τ;I为四旋翼的惯性矩阵。τ表示通过控制电机转速所产生的力矩;d为系统的不确定性,d=[dx,dy,dz]Τ,它包括2 部分,一部分是未建模动态,如陀螺力矩、机体部分坏损、负载和气动阻力等;另一部分是可能存在的内部或外部未知时变扰动。
d可以表示为
式中:Ir代表电机的转动惯量;R1为̇与ω之间的转换矩阵,由式(31)可得
即
在实际中,对四旋翼的姿态控制基于小角度假设,即
从而可得
基于DJI F450 模型所得到的各个参数及其物理意义如表1 所示。
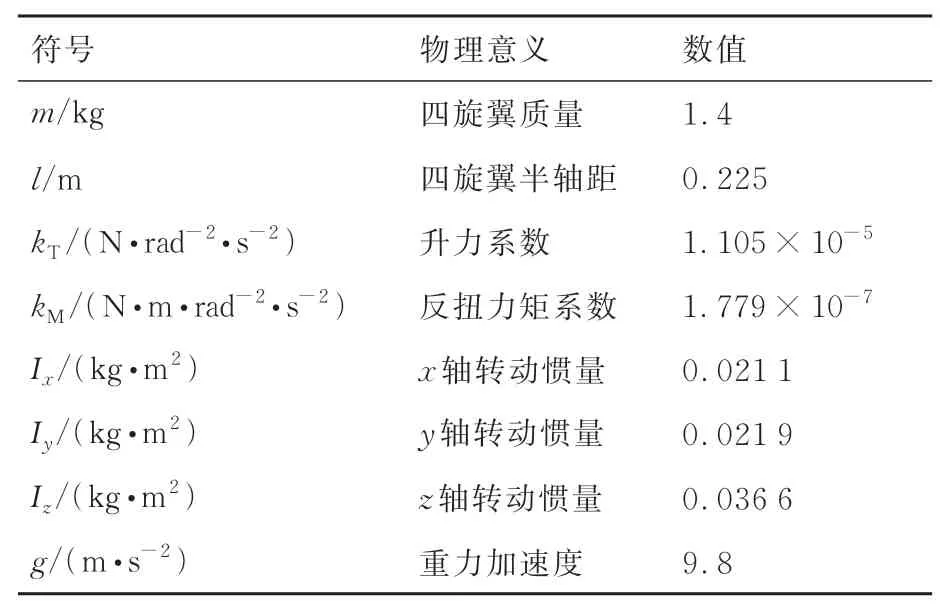
表1 DJI F450 各物理参数及取值Table 1 DJI F450 physical parameters and values
对于图6 所示的“×”型四旋翼飞行器机体坐标系的转矩控制量可以表示为
由于四旋翼的姿态角和推力只与FT、τx、τy和τz有关,因此姿态控制器设计过程中只需要考虑设计FT、τx、τy和τz的控制律。
4 闭环控制器设计
4. 1 模型补偿控制器设计
针对四旋翼飞行器的姿态系统,假定模型函数未知,或者部分已知,本节设计了基于CFO 的模型补偿控制(Model Compensation Control,MCC)策略的闭环控制器。MCC 基于非线性极点配置控制,使用未知模型的估计值̂补偿未知函数f。
实际控制中,f=fk+fu,其中fk为已知部分,fu为未知部分,可以用R-CFO 的式(21)得到,需要注意的是,需要将式(21)中的bu,替换成fk+bu,则估计值为,其他不变,如果考虑f完全未知,可以直接采用式(21)。补偿控制就是用̂补偿真实的f,或用̂ 补偿fu,主动抵消该未知量在控制中的影响。
因此本文使用基于极点配置的MCC,利用R-CFO 估计未知模型并主动抵消该未知量在控制中的影响。图7 为四旋翼比例一串级控制器的结构框图。
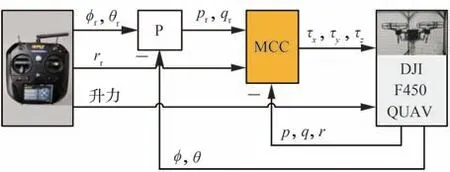
图7 四旋翼飞行器系统控制结构Fig. 7 Control structure of quadrotor flight vehicle system
考虑系统方程式(2),给定参考信号yr,设定跟踪误差为,其中下标c表示控制跟踪误差,以区别观测器误差,误差向量为ec=[ec1,ec2]Τ。由式(2)可知,跟踪误差方程为
式中:参数k2、k1使误差方程的特征多项式s2+k1s+k2为Hurwitz 多项式,可根据期望的极点配置设计。假定f未知,依赖观测器与控制器设计分离原理[27],先依据观测数据估计系统未知模型函数f;如果部分未知,就估计其中的部分未知项,包含扰动、耦合和时变部分,再把估计值看成真实值,按照确定性系统设计控制器。
提出的基于R-CFO 的模型补偿控制器,即MCC 为
注意到,基于R-CFO 的模型补偿控制仅利用系统的期望输入信号和输出信号,控制器可以不依赖于系统模型,或者不依赖于部分未知模型和扰动。通过R-CFO 估计未知模型函数值,在线反馈补偿给控制器。该模型补偿控制器和补偿函数观测器的参数均具有实际的物理意义,所以容易根据特性需求选取。
4. 2 姿态环串级控制器设计
对该飞行器系统,本文采用控制策略为内外环的串级控制,外环采用比例控制,内环采用基于R-CFO 的模型补偿控制。实际姿态实验中遥控器的4 个通道指令分别转化为滚转角、俯仰角的参考指令,偏航角速度参考指令和升力指令,因此外环只需考虑滚转角和俯仰角的跟踪控制。设计的滚转角和俯仰角的角速度指令为
由式(35)和式(36),系统姿态内环模型可以描述为
式中:fp、fq和fr是每个子系统未知模型函数;Ix、Iy和Iz是四旋翼3 个轴上的转动惯量,但是如果有参数测量误差,也可以设为系统相关可调的参数。
系统小角度假设造成的误差、扰动、未建模动态和负载变化都隐含在fp、fq以及fr中,因此,提出使用R-CFO 进行补偿控制,和为3 个通道未知非线性模型项的估计值。由式(42),可以给出一阶模型的补偿控制器,即
可推导出3 个姿态角的控制律分别为
式中:kp、kq和kr是内环角速度误差增益;bp、bq和br是系统相关的未知可调的参数;和为参考角加速度,可由高阶微分器(High Order Differentiator,HOD)得到[7,22]。
HOD 可以设置为任意阶系统,可对任意阶信号提取微分。本文采用了三阶结构,如图8 所示,通过HOD 可以估计参考输入的微分以及二阶微分信息,其中xi(i=1, 2, 3) 为HOD 的状态。
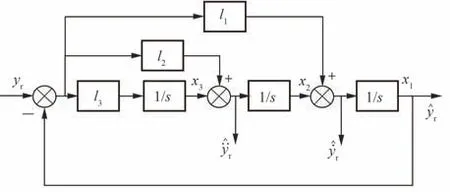
图8 HOD 结构Fig. 8 HOD structure
根据图8 可得由输入量yr估计其各阶导数的输出方程。三阶微分器的输出方程为
4. 3 闭环系统稳定性和收敛性分析
四旋翼飞行器姿态系统中,每个子系统的模型都可以用如式(46)和式(47)所示的二阶系统描述(以俯仰角为例):
或
定义姿态角跟踪误差为eθ=θr-θ,角速度跟踪误差为eq=qr-q。针对该二阶系统,设计的基于R-CFO 的MCC 双闭环串级控制策略为
定理2基于R-CFO 的模型补偿控制器(式(46))控制四旋翼飞行器跟踪参考姿态角,能实现闭环系统稳定,姿态跟踪误差渐近收敛。
证明令E=[eθ,eq]Τ,假设=0,将控制器(48)代入系统(44)中,可得
有
得到闭环系统矩阵表达式为
定义R-CFO 对未知函数的估计误差为ef=-f,式(51)可写为
设计Lyapunov 函数为
P是对称正定矩阵且满足如式(54)所示的Lyapunov 方程:
Q>0,取,则有
从而有
式中:ε为RBF 神经网络网络逼近误差,能够充分小,因此V̇≤0。证毕。
5 数值仿真分析
5. 1 函数观测器性能比较
在实际控制中,由于未建模动态,如陀螺力矩、机体部分坏损、负载和气动阻力等,可能存在的内部或外部未知时变扰动对无人机的影响,因此对非线性模型项的高精度估计尤为重要,因此分2 种情况讨论。
案例1观测器对3 种简单函数的观测性能
先介绍一下扩张观测器(ESO),表达式为
由式(57)可知,当bu=0 时可得ESO 的特征方程为
选取a=8,即ESO 的参数为l1=24,l2=192,l3=512。为了对比公平,让ESO 与CFO的特征多项式常数项相等,都等于512。由式(13)和式(14),可以确定ω=3.174 8。因此式(13)的参数l1=28.57,l2=121,λ=4.23,得到CFO 的特征多项式s3+28.57s2+242s+512。 本文提出的 R-CFO,同样取l1=28.57,l2=121,γ=0.001。
对于系统式(1),在仿真过程中令bu=1,令模型函数项f=1,t, 0.5t2, sin 3t,分别用ESO、带有积分器的CFO 和R-CFO 进行估计,结果如图9 所示。为了统一,第5 节图9~图11 中和分别代表各观测器对模型函数项的估计值,f代表实际值。

图9 ESO 和R-CFO 关于不同函数的估计Fig. 9 Estimation of ESO and R-CFO on different functions
图9(a)显示,对于常值函数,ESO、CFO 和R-CFO 都能实现无差估计;但是,图9(b)表明,对于斜坡函数,ESO 估计的稳态误差为0.375,而CFO 和R-CFO 估计的稳态误差为零;图9(c)表明,对于抛物线函数,ESO 估计的稳态误差随着时间无限增大,估计的误差发散,而CFO 和RCFO 仍能实现无差估计;由图9(d)可知,对于更为一般的函数,CFO 和R-CFO 的估计性能远高于ESO,并且对于非线性三角函数R-CFO 的收敛速率快于CFO。在图9 中,ESO 的平均绝对值误差为0.595 2,CFO 的平均绝对误差为0.023 9,而R-CFO 为0.007 1。
案例2对强非线性系统模型项的估计
由于无人机属于强非线性系统[28],故考察RCFO 对强非线性模型项的观测性能,并与ESO进行对比。考虑非线性Duffing 系统
式中:时变非线性未知函数为f=25ẏ-y3+11cost+sin(πy)sin(πẏ)+5sint,令bu=3sint,2 种观测器的参数选择与案例1 相同。ESO、CFO 和R-CFO 关于Duffing 模型函数估计性能对比如图10 所示。

图10 ESO、CFO 和R-CFO 关于Duffing 模型函数估计性能对比Fig. 10 Comparison of ESO, CFO and R-CFO on Duffing model function estimation performance
图10(a)和图10(c)表明,ESO 对该Duffing系统中未知函数的估计有明显的相位差。在尖峰处,跟踪严重不足,误差范围在[-100, 100],说明其对高频非线性函数估计误差较大;而R-CFO 估计精度高,即使在尖峰处也能高精度估计,误差范围在[ -5, 5]。
由图10(b)和图10(c)对比可知,相对于CFO,R-CFO 将误差范围进一步缩小,观测精度更高。R-CFO 对该系统模型函数的估计平均绝对误差为0.785,而ESO 为19.644,CFO 是3.341。
5. 2 四旋翼飞行器姿态角跟踪仿真测试
被控对象为四旋翼飞行器式(41),将设计的模型补偿控制(MCC)策略应用于四旋翼飞行器的姿态控制,并与PID、ADRC 控制方法比较。模型参数由表1 给出。系统的初始状态取Θ0=ω0=0。为了对比的公平性,数值仿真中3 种控制算法外环采用的比例控制参数均为kθ=6.5。通常,ADRC 控制律表达式为
而基于R-CFO 的MCC 控制律为式(42),其中所估计与ADRC 不同;另外,ADRC 控制律式(60)中一般没有。3 种内环控制器选取参数在表2 中给出。以滚转通道为例,给定设置为ϕr=0.12 rad,在3 ~5 s 之间加入外部扰动dϕ0=0.05 sin5t。
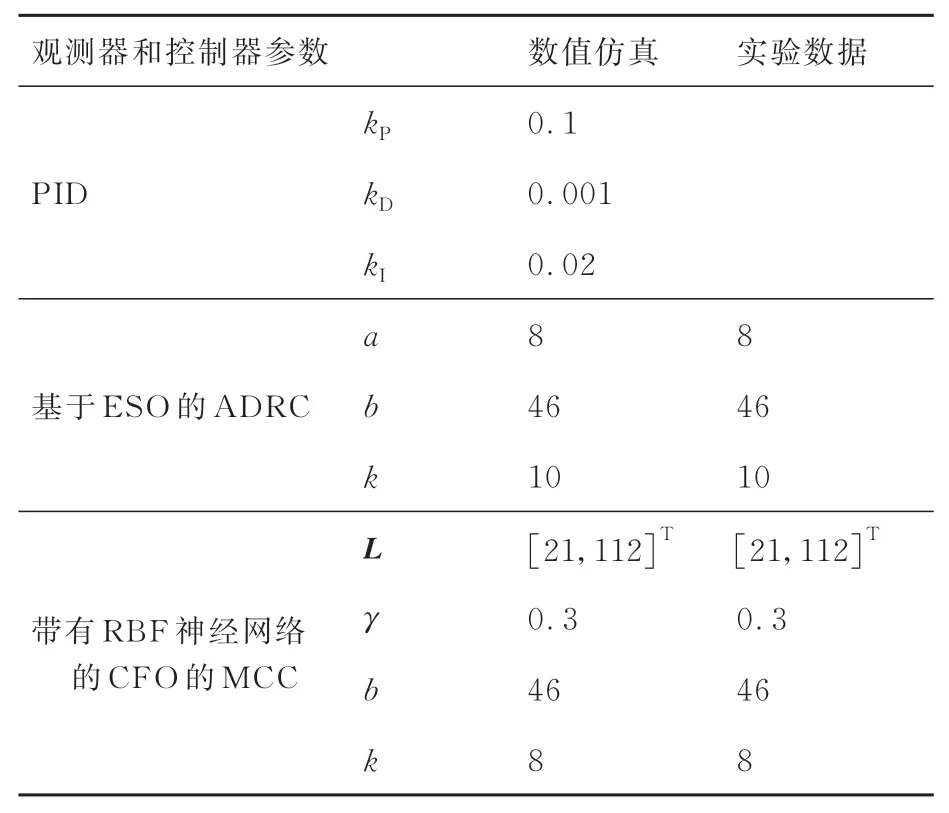
表2 内环控制器参数Table 2 Inner loop controller parameters
滚转通道控制及估计的对比如图11 所示。对滚转角系统控制和未知模型估计的对比如表3所示。

表3 对滚转角系统控制和未知模型估计的对比Table 3 Comparison of roll angle system control and unknown model estimation
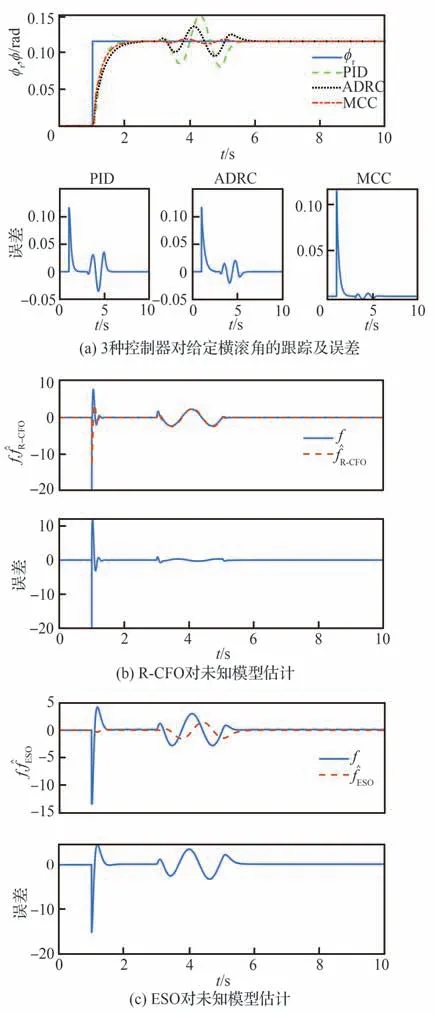
图11 滚转通道控制及估计的对比Fig. 11 Comparison of roll channel control and estimation
从图11(a)和表3 看出,对于阶跃给定,MCC对扰动的抑制效果最好,ADRC 抑制扰动的性能也明显优于PID。由图11(b)和图11(c)及表3 看出,对于未知模型的估计,R-CFO 估计的精度最高。仿真发现,为了提高控制性能,增大ESO 参数,使得ADRC 方法控制性能有所提高,但是控制性能仍达不到MCC 的效果。因此本文所提出的MCC 能以较小参数实现较优越的控制性能和抗干扰性能。
6 实验验证
实验中利用基于Pixhawk 的四旋翼飞行器控制算法开发平台实现四旋翼内部算法更新,流程如图12 所示。选择MCC 控制作为内环姿态控制器,四旋翼的结构如图6 所示。

图12 基于Pixhawk 的四旋翼算法开发平台Fig. 12 Four-rotor algorithm development platform based on Pixhawk
本实验主要考察四旋翼对跟踪横滚角的性能,参考值通过遥控器给定。实验过程中,首先保证悬停四旋翼飞行器在万向节底座上的初始状态约为[ϕ0,θ0,ψ0]Τ=[0,-0.61,0]Τrad,参考的初始状态为[ϕr0,θr0,ψr0]Τ=[0,0,0]Τrad,四旋翼飞行器在万向节底座上的滚转角和俯仰角最大值为ϕmax=θmax=±0.61 rad。期望角度由遥控器输出,控制器参数由表2 给出。
本组实验测试2 种控制算法跟踪任意给定参考的性能,滚转角的参考值ϕr通过遥控器实时给出,由式(61)给出,即
式中:rc 代表遥控器的滚转通道摇杆量,对应PWM 值的范围是1 100 ~1 900 μs。首先通过遥控器的油门通道使机体到达参考的初始姿态[ϕr0,θr0,ψr0]Τ=[0,0,0]Τrad,并保持悬停一段时间,由遥控器控制改变参考值。基于MCC 和ADRC 的控制算法跟踪参考滚转角的结果如图13 所示,跟踪随机给定信号的平均绝对误差由表4 所示。

表4 MCC 与ADRC 控制性能对比Table 4 MCC and ADRC control performance comparison
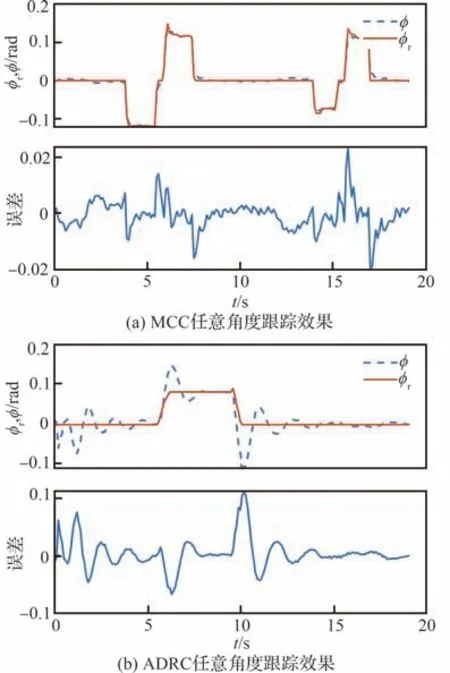
图13 滚转角2 种控制算法跟踪效果对比Fig. 13 Comparison of tracking effects of two control algorithms for roll angle
图13(a)和图13(b)显示,对于任意给定,ADRC 和MCC 都能实现高精度跟踪。但是,对于阶跃信号,由于ESO 的高频噪声问题,所以ADRC 在控制过程中会产生振荡并出现超调。而图13(a)表明,由于R-CFO 观测精度高,故MCC 能够更快收敛且无超调。结合表4 数据可知MCC 无论是在跟踪的稳态性能还是暂态性能都要强于ADRC。
下面给出抗扰实验结果。对于MCC 和ADRC 实验,在飞行器机体左侧悬挂同一重物,实验前先将其托起,使它不影响飞行器的正常启动和悬停。当飞行器启动并悬停一段时间后,瞬间释放该悬挂的重物,并保持重物加载,以模拟机体可能受到的外部扰动。2 种控制算法的抗扰测试结果如图14 所示。
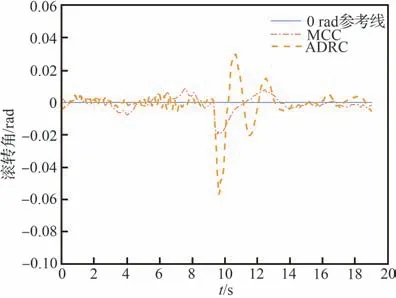
图14 滚转角2 种控制算法跟抗扰果对比Fig. 14 Comparison of disturbance rejection of two control algorithms for roll angle
由图14 可以看出,总体MCC 控制优于ADRC,稳态误差较小。在大约9 s 处,无人机受扰,与MCC 相比,ADRC 控制下的滚转角产生了大得多的受扰振荡,克服扰动的调节时间也更长,不能快速重新回到原来的平衡位置。这是由于R-CFO 对未知模型函数的估计值更为精确,并将估计值及时反馈给控制器以平衡抵消该扰动,因此MCC 较ADRC 的受扰超调小得多,调节时间更短,以更高精度重新回到平衡状态,抗扰能力得到了很大的提升。
该组实验与图11 所示的仿真结果相比,在控制器参数类似的情况下,其中ADRC 的暂态表现出明显超调和振荡。由于ESO 的观测器参数较小,面对实际系统中更大的不确定性还需要继续增大参数来提高估计精度,更容易引入高频噪声,由于超调量以及振荡的存在,导致调节时间更长。相比之下,MCC 在选择与仿真时相近的观测器参数条件下,MCC 调节时间更短,几乎没有超调,而ADRC 的最大超调达到了58%,稳态精度方面,MCC 具有更强的鲁棒性。
7 结 论
1)基于无人机各个通道之间的强耦合,负载时变,强风干扰等特性,提出了一类不依赖模型的控制策略。本文用RBF 神经网络替代了CFO 中的线性滤波补偿,设计了带有RBF 神经网络的补偿函数观测器(R-CFO),提高了估计精度,基于Lyapunov 函数给出了收敛性证明。
2)基于所提出的R-CFO 对未知模型的估计,本文提出了模型补偿控制策略(MCC),以补偿模型偏差、时变和各类扰动,给出了闭环系统控制稳定性的证明。通过几个确定非线性函数的仿真测试,表明基于带有RBF 神经网络的CFO 估计精度大幅优越于ESO 估计。
3)通过四旋翼无人机的数值仿真测试以及实际实验发现,模型补偿控制较现有的自抗扰控制(ADRC)在跟踪性能更优越,稳态精度更高,鲁棒性强。

