试车台供气压缩机组并网控制方法

董彦钊，周延，*，邹继贤，王信，，李晓冬，崔洪帅

1．西安交通大学 能源与动力工程学院，西安 710049 2．中国航发四川燃气涡轮研究院，绵阳 621703

航空发动机高空模拟试车台（试车台）是一种能够在地面环境下模拟航空发动机多种高空飞行条件的实验装置，是综合测试航空发动机的装备［1］。航空发动机研发过程中的各方面问题与性能参数都需要经过试车台模拟实验的反复调试验证，对于自主研发高性能航空发动机而言，试车台是必不可少的关键设备。

20 世纪60 年代以来，西方发达国家基于大型飞行器发展的需求，先后建造多个试车台［2-6］，美国、英国、法国、德国、俄罗斯分别拥有各自的试车台，且美国拥有的试车台以及高空舱数量依然占据全世界的半数之上。依靠半个世纪以来的发展，西方发达国家已经对试车台在理论建模［7-12］、控制方法［1，13-15］、设备优化［16-19］等多个方面进行了深入而广泛的研究。中国出于国防工业与航天事业的需求，试车台的设计与建设水平也在迅速提高，正在快速缩小与西方发达国家的差距。

美国阿诺德工程发展中心（AEDC）的ASTF试车台是目前为止规模最大的试车台［3，5］，建成于20 世纪80 年代中后期，气源装机功率达到450 MW。自建成至今进行了一系列优化升级，使用MATLAB/Simulink 完成了试车台的建模，并且能够实现实时仿真，缩短了实验过程的调节时间，提高了设备控制精度［9，18-19］。除此之外，美国国家航空航天局（NASA）、德国斯图加特大学等机构的学者同样对试车台进行了深入的研究［4，8，11，13，16，20］，极大推进了试车台设备的发展。

国内的高空模拟实验基地始建于1965 年，并于1995 年竣工。1997 年成立航空发动机高空模拟航空科技重点实验室后，高空模拟实验水平有了显著的提升。张松［21］和但志宏［22］等对试车台进、排气调压系统复合控制方法进行了深入研究，并成功搭建了进、排气调压系统半物理仿真试车平台［23-24］；朱美印等则提出多种飞行环境模拟建模方法［25］与控制方法［26-29］。但是这些研究主要针对试车台实验舱部分，缺乏对供气压缩机组的研究。

目前中国的试车台供气压缩机组并网主要依靠人工操作，导致供气压缩机组并网过程存在耗时长，对并网操作人员要求高，抗干扰能力弱等问题。因此，亟需开展航空发动机高空模拟实验台控制策略方面的研究。

专家系统是人工智能领域的重要分支，产生于20 世纪60 年代，其定义为：使用人类专家推理的计算机模型分析复杂现实问题，并得到与人类专家一致的结论［30］。自1968 年Feigenbaum 等开发出首个专家系统DENDRAL［31］以来，专家系统的发展经过了5 个阶段［32］：基于规则的专家系统［31，33-37］、基于框架的专家系统［38-40］、基于案例的专家系统［41-43］、基于模型的专家系统［44-47］、基于网络的专家系统［48-49］，主要功能类型包括诊断型、预测型、教学型、规划型与控制型等，并在多个领域得到了应用。据调查，在商业领域与工业领域，专家系统的应用占比约为60%，而在英国，约有24%的专家系统服务于财政部门。专家系统作为计算机系统非数值问题求解的重要途经，得到了广泛的关注，美国、日本、英国等都将其作为国家重点科研项目。

本文以某型试车台供气压缩机组为研究对象，建立该供气压缩机组机理模型，并依靠专家系统，设计试车台供气压缩机组并网流程与控制方法，最终在MATLAB/Simulink 平台上搭建动态仿真模型，实现供气压缩机组并网控制仿真，并进行验证。

1 试车台供气压缩机组动态建模方法

试车台供气压缩机组结构如图1 所示，包含压缩机，入口阀、回流阀、排空阀、高温供气阀与低温供气阀共5 个阀门，压缩机前、后管网。机组上游为大气，下游为供气总管。

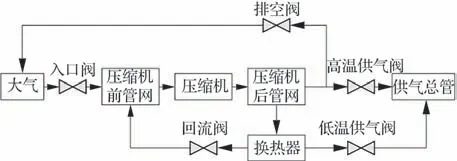
图1 试车台供给机组Fig. 1 Air supply compressor unit of altitude test facility

1. 1 压缩机动态模型

压缩机是试车台供气压缩机组中的核心部件。本文中压缩机模型综合参考了Greitzer 模型［50］与Gravdahl 模型［51］，通过质量守恒、动量守恒与能量守恒，推导出压缩机动态控制方程。图2 所示为压缩机模型示意图，该压缩机模型包含抽象化压缩机、等效容腔、等效阀门等部件。其中将压缩机抽象化，抽象化压缩机内不包含容腔，由无量纲化性能曲线表示升压过程。

图2 压缩机模型示意图Fig. 2 Schematic diagram of compressor model

图2 中，以压缩机及其后等效容腔为控制体，pin为压缩机入口压力；Gin为进入该控制体的工质质量流量；Tin为压缩机入口温度；ψ为压缩机进出口压比；A为压缩机等效通流面积；L为压缩机等效通流距离；p2为工质经过压缩机升压后压力，此时工质还未进入等效容腔；pp为等效容腔内压力；Vp为等效容腔容积；Gout为离开该控制体的工质质量流量。可以得到三大守恒方程（质量守恒方程、动量守恒方程与能量守恒方程）：

式中：ρ为等效容腔内工质密度；G为压缩机流量，稳态时，G=Gin=Gout；Cx为压缩机内工质轴向流速；q′′为通过控制体的轴向传热量；p′为轴向上单位长度控制体的轴功；q′为轴向上单位长度控制体的传热量；M为控制体内工质总质量；e为控制体内工质比能量；h为工质经过控制面的对流传热焓。

整理后得到压缩机模型为

式中：a为压缩机入口声速；hin为进入控制体工质焓值；Tp为等效容腔内温度；hout为离开控制体工质焓值；Pw为控制体对外做功；q为控制体与外界换热量；cp为控制体内工质定压比热容。

1. 2 管网动态模型

根据文献［52］，由于压缩机前后管网存在多路进出流量，认为此时的管网模型适用混合器容腔模型，并且认为离开容腔的工质状态与容腔内工质状态一致，如图3 所示。

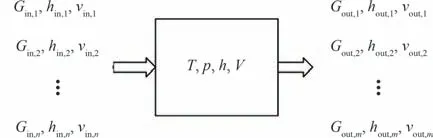
图3 管网模型示意图Fig. 3 Schematic diagram of pipeline module

图3 中，T为容腔内工质温度；p为容腔内工质压力；h为容腔内工质焓值；V为容腔容积；多路排气时认为工质的排气焓值与容腔内工质焓值相等，即h=hout，1=hout，2= … =hout，m，其中hout，1，hout，2，…，hout，m为容腔排气焓值。由于前后容腔结构存在差异，对混合容腔模型进行扩展，得到微分方程如下：

式中：cp为容腔内工质定压比热容；h为容腔内工质焓值；R为工质气体常数；Q为单位时间内容腔与外界的换热量；假定共有n路工质进入该容腔，Gin，i表示第i路工质质量流量，hin，i表示第i路工质焓值，vin，i表示第i路工质流速，i∈［1，n］；假定共有m路工质离开该容腔，Gout，k表示第k路工质质量流量，vout，k表示第k路工质流速，k∈［1，m］。

1. 3 换热器动态模型

该供气压缩机组所用换热器基本结构如图4所示，分为外壳、高温工质（壳侧）、换热管、冷却水（管侧）4 个部分，高温工质与冷却水采用逆流方式布置。

图4 换热器模型示意图Fig. 4 Schematic diagram of heat exchanger module

图4 中，Tshell为外壳平均温度；Ts为高温工质平均温度；Tt为换热管平均温度；Tw为冷却水平均温度；Gs为高温工质质量流量；ps为高温工质压力；Ts，in为高温工质入口温度；Ts，out为高温工质出口温度；Gw为冷却水质量流量；Tw，in为冷却水进水温度；Tw，out为冷却水排水温度；Qenv为外壳对环境散热量；Qshell为高温工质对外壳的换热量；Qt为高温工质对换热管的换热量；Qw为换热管对冷却水的换热量。4 个部分分别作为控制体建立动态方程，且为了简化模型以方便求解，做出如下假设：

1） 忽略高温工质在换热器内压降，则守恒方程中无动量方程。

2） 各控制体以集总参数法处理，以平均温度作为该控制体温度。

3） 各控制容积间的传热按照算数平均温差计算。

4） 由于高温工质降温过程中冷凝水量相对工质总量极小，忽略高温工质降温过程中产生冷凝水导致的密度变化，即高温工质侧进出流量一致。

高温工质（壳侧）模型：

式中：ρs为高温工质平均密度；Vs为壳侧容积；hs为高温工质平均焓值；hs，in为进入壳侧工质焓值；hs，out为离开壳侧工质焓值。Qt与Qshell表达式为

其中：as，t为高温工质对换热管总传热系数；As，t为高温工质与换热管换热面积；as，shell为高温工质对外壳总传热系数；As，shell为高温工质与外壳换热面积。

壳侧工质排出温度为

冷却水（管侧）模型：

式中：ρw为冷却水平均密度；Vw为管侧容积；Gw为冷却水流量；hw为冷却水平均焓值；hw，in为冷却水进口焓值；hw，out为冷却水出口焓值；Qw表达式为

式中：aw，t为换热管对冷却水总传热系数；Aw，t为换热管与冷却水换热面积。

冷却水的排水温度为

金属部分模型：

换热管与外壳为金属材质，其能量方程为

式中：Mt为换热管质量；ct为换热管比热；Mshell为外壳质量；cshell为外壳比热。Qenv表达式为

式中：ashell，env为外壳对环境总传热系数；Ashell，env为外壳与环境换热面积；Tenv为环境温度。

1. 4 阀门模型

根据文献［53］，将蝶阀等效为节流孔板的情况下，对于空气等可压缩流体，绝热等熵条件下流体经过节流孔板的质量流量公式为

式中：Qm为阀门质量流量；p1为阀前压力；p2为阀后压力；Δp为阀门前后压差；ρ1为阀门上游工质密度；A为阀门节流孔面积；k为工质绝热指数；u为流束收缩系数；d为调节阀截面面积与管道截面面积比值。式（19）较为复杂，且实际阀门由于结构不同，流束收缩系数与节流孔通流面积有较大差异，因此采用简化公式：

式中：ϕ为流量系数，与阀门开度、阀门结构以及上下游压差相关。通过实验以及CFD 计算获得不同工况下的阀门节流孔面积与流量系数。

1. 5 阀门执行机构模型

目标供气压缩机组所使用阀门执行机构为非伺服调节阀，只可接受开度增大或减小信号并以固定速度动作，而无法通过给定阀位的方式进行阀位调节。因此建立阀门执行机构模型为

式中：c为阀门阀位；vc为阀门动作速度；S为开关信号，增大阀位时，S= 1，减小阀位时，S= -1，保持阀位不动时，S= 0。

1. 6 建模误差

由于目前对大通径管网与阀门的质量流量动态测量存在困难，设备对于各阀门与压缩机未设置对应的质量流量测量装置，同时换热器进出口温度与压缩机出口温度同样未设置相应的测点。现对比压缩机入口压力、温度，压缩机出口压力，以及阀门执行机构的仿真结果与实验结果之间的建模误差，如图5～图8 所示。

图5 压缩机入口压力建模误差Fig. 5 Error of compressor inlet pressure

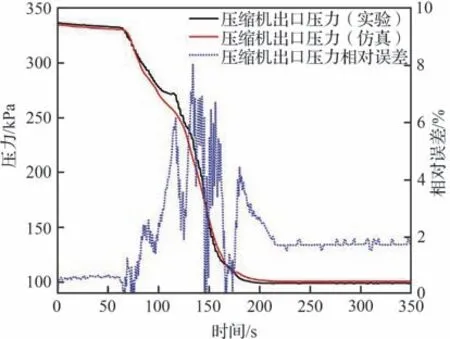
图6 压缩机出口压力建模误差Fig. 6 Error of compressor outlet pressure

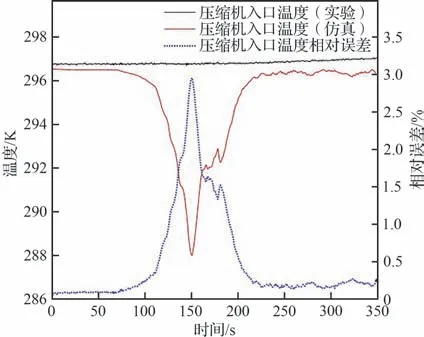
图7 压缩机入口温度建模误差Fig. 7 Error of compressor inlet temperature

压缩机入口压力动态过程中，仿真结果与实验结果最大相对误差为8.64%，平均相对误差为1.54%。压缩机出口压力动态过程中，仿真结果与实验结果最大相对误差为8.05 %，平均相对误差为1.62 %。压缩机入口温度动态过程中，仿真结果与实验结果最大相对误差为2.95%，平均相对误差为0.68%。阀门执行机构动态过程中，仿真结果与实验结果最大相对误差为3.41%，平均误差为0.58%。

2 控制策略

由于该供气压缩机组中阀门无法准确给定阀位，且只可以固定速度动作，因此所设计并网控制策略采用专家系统。专家系统是一种模拟人类专家的控制知识与经验搭建的控制系统［54］，利用该系统，能够充分利用历史运行数据，提高所设计的控制器的可靠性。专家系统主要包括如下几个部分：知识库、规则库、数据库、推理机［55］。该专家系统通过对实际采集和分析压缩机工作情况、各阀门阀位等信息，经过推理机分析现有信息，从而找到最佳控制方案。专家系统组成如图9 所示。

2. 1 知识库与数据库

知识库与数据库内包含该机组历史运行数据，操作人员基于经验获得各阀门的阀位变化对系统状态的影响。基于知识库与数据库，能够对机组将来状态进行适当预测，同时随着机组的运行，不断更新的运行数据能够提高知识库与数据库对机组状态预测的精度。同时，利用历史数据可以对供气压缩机组仿真模型进行修正，并通过供气压缩机组仿真模型的运行快速扩充数据库，使该系统控制质量不断提高。由于机组硬件设备限制，该专家系统中数据库包含的信息如表1所示。

表1 数据库内容Table 1 Database contents

由于目前设备暂无进行各部分动态质量流量实时测量的条件，数据库中各阀门与压缩机流量数据通过实时测量的压力、温度、阀位等数据结合阀门与压缩机的仿真模型通过实时仿真计算获得。

依据数据库中的历史运行数据，获得供气机组中阀门的阀位变化与上下游管网参数对机组压比的影响。进一步通过最小二乘法等拟合方式量化各部分状态对压比变化的影响，得到压比变化关于各阀门的阀位、流量、管网压力、温度等参数的多项式表达式，从而实现依据当前系统状态对压比变化的实时预测。

2. 2 规则库

规则库是专家系统的核心，通过提炼专家知识设计控制规则，是推理的依据。本系统中，基于供气压缩机组并网操作流程规范与历史运行数据，将并网过程分为2 个阶段，并分别建立控制规则。并网过程2 个阶段特征如图10 所示。

图10 供气压缩机组并网过程不同阶段Fig. 10 Different stages of grid-connection process of air supply compressor unit

控制过程判断依据设计以机组压比Pr为主，综合参考系统中其他关键参数（压缩机流量G、压缩机功率P、压缩机转速ω等），记为P*r=f(Pr，G，P，ω，…)：

式中：α1，α2，α3，…及β为其他关键参数的影响系数，针对不同的机组，不同的参数其系数大小不同，由历史运行数据分析获得。

同时记供气压缩机组防喘压比为Pr，C以及防喘安全裕量为ΔPr，C，建立控制规则如图11 所示，并使用MATLAB 语言进行编程。

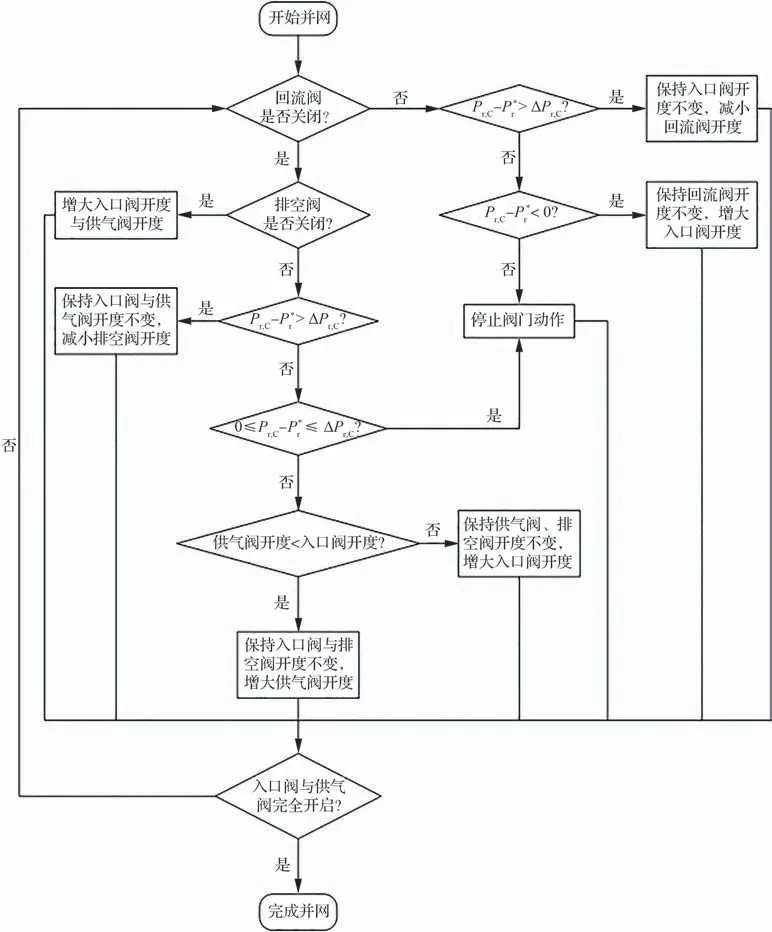
图11 控制规则Fig. 11 Control rules

2. 3 推理机

推理机是专家系统中的思维推理工具，其基于专家系统的知识库、数据库以及控制规则，完成最佳控制方案的求解。在本文中，由MATLAB 软件中的“if”语法结构功能来构造推理机算法，进而实现推理机功能。推理机实时读取供气机组采集的设备运行情况，匹配知识库中的历史运行数据，得到机组压比变化趋势的预测信息，并依据控制规则给出各阀门控制指令，令机组在并网过程中压比始终维持在安全范围之内，确保机组自动化并网过程的安全、快速。

3 仿真结果与实验结果对比

3. 1 控制仿真

为验证本文提出的并网控制方法，进行并网仿真，初始状态下供气压缩机组处于回流状态，入口阀完全关闭，回流阀开度为70%，排空阀完全开启，供气阀完全关闭，并网过程中选择低温供气阀作为机组并网供气所用阀门，高温供气阀保持关闭。大气压力为97.5 kPa，环境温度为296.5 K，换热器冷却水给水温度与环境温度一致。实验所用机组目前尚无法直接使用该控制方法进行并网，选择采用仿真过程中阀位指令信号作为实验的阀位指令信号，进行并网实验。并网过程阀门指令与阀位如图12～图15 所示。

图12 阶段1 阀门控制指令Fig. 12 Stage one valve control command

图13 阶段1 阀门阀位Fig. 13 Stage one valve position

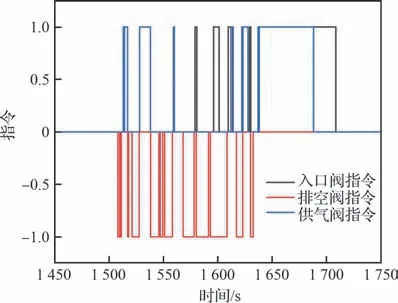
图14 阶段2 阀门控制指令Fig. 14 Stage two valve control command

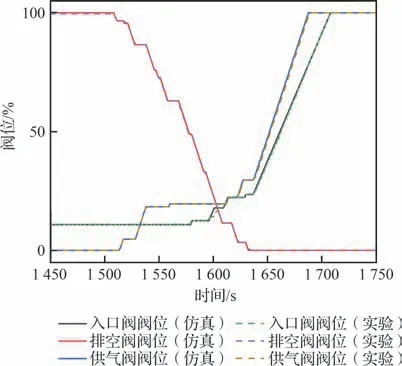
图15 阶段2 阀门阀位Fig. 15 Stage two valve position

阶段1 时间为100～200 s，阀门动作以关闭防喘阀为主，入口阀起辅助调节作用，避免供气压缩机组压比过高进入喘振状态。阶段1 耗时＜100 s，最终回流阀完全关闭，入口阀开度为12.5%。

阶段2 时间为1 450～1 750 s，排空阀完全关闭后，入口阀与供气阀完全开启，过程中排空阀、供气阀与入口阀交替动作维持供气压缩机组状态稳定。整个阶段2 耗时＜300 s。

3. 2 结果对比

仿真结果与实验结果对比如图16～图18 所示。并网过程压力变化如图16 所示。并网开始前，压缩机入口仿真初始压力为35.57 kPa，实验初始压力为33.32 kPa。并网过程中阶段1 压缩机入口仿真最大压力为35.57 kPa，最小压力为29.07 kPa；实验最大压力为43.20 kPa，最小压力为31.64 kPa；阶段1 结束后压缩机入口仿真稳态压力为35.97 kPa，实验稳态压力为34.11 kPa。压缩机入口压力仿真与实验结果变化趋势一致。压缩机出口仿真初始压力为95.49 kPa，实验初始压力为95.31 kPa；并网过程中压缩机出口仿真最大压力为97.84 kPa，最小压力为95.49 kPa；实验最大压力为100.2 kPa，最小压力为95.31 kPa；阶段1 结束后压缩机出口仿真稳态压力为97.84 kPa，实验稳态压力为97.93 kPa。压缩机出口压力仿真与实验结果变化趋势一致。阶段2为供气压缩机组建立背压及升压的过程，该过程中供气压缩机组压缩机入口压力与出口压力升高，最终完成并网。完成并网后压缩机入口压力仿真值为93.34 kPa，实验值为93.42 kPa；压缩机出口压力仿真值为337.6 kPa，实验值为338 kPa。

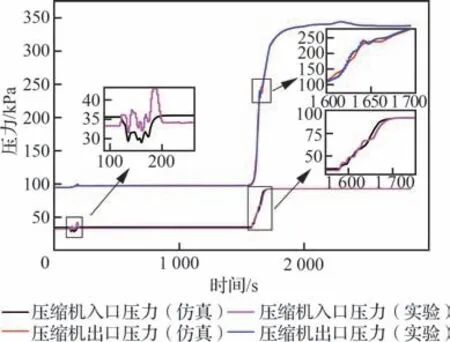
图16 供气压缩机组并网过程压力变化Fig. 16 Pressure change during grid-connection of air supply compressor unit

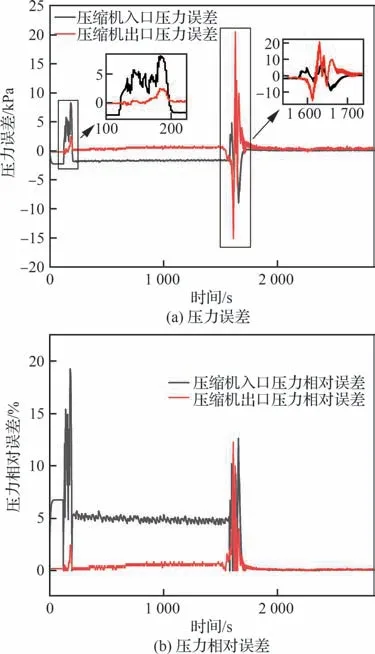
图17 仿真压力与实验结果误差Fig. 17 Pressure error between simulation and experimental results

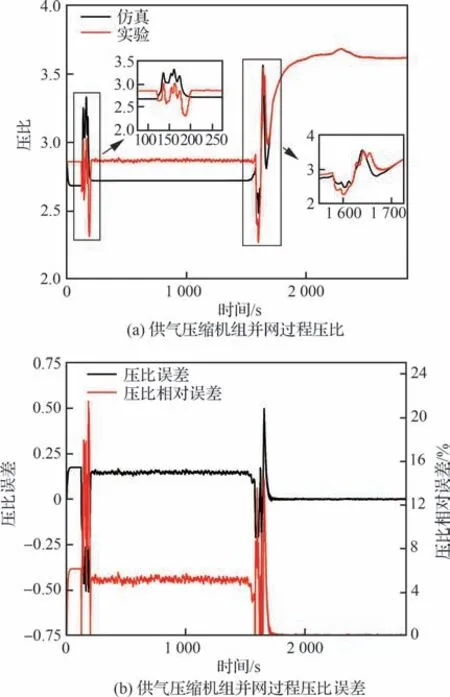
图18 供气压缩机组压比仿真结果与实验对比Fig. 18 Comparison of simulation and experimental results of air supply compressor unit pressure ratio

由图16 与图17 可见，并网过程中压力仿真结果与实验变化趋势一致，压缩机入口压力平均误差为1.15 kPa，平均相对误差为3.12%，压缩机出口压力平均误差为0.65 kPa，平均相对误差为0.44%。阶段1 压力误差主要出现在回流阀关闭过程中，该过程中压缩机入口压力变化仿真结果与实验变化趋势一致。阶段1 完成后仿真结果与实验结果稳态压力符合良好，压缩机入口压力稳态误差为0.63 kPa，压缩机出口压力稳态误差为1.67 kPa。阶段1 压缩机入口压力最大误差为8.18 kPa，最大相对误差为19.26 %；压缩机出口压力最大误差为2.40 kPa，最大相对误差为2.44 %。阶段2 过程中压缩机前后管网压力仿真结果与实验结果变化趋势一致，而压力误差大于阶段1，压缩机入口压力最大误差为8.87 kPa，压缩机出口压力最大误差为20.49 kPa。对比图15 可知，此时排空阀完全关闭，入口阀与供气阀开度皆＜30%，且开度开始迅速增大。另一方面，在相同控制信号下，对比仿真阀位与实验阀位，二者间存在差异，因此在并网过程中，尤其是阀门动作时，仿真阀位与实验阀位不同，导致压力仿真结果与实验结果间存在误差。

供气压缩机组并网过程压比仿真结果与实验结果变化趋势一致。仿真中机组初始压比为2.67，最终稳态压比为3.62；实验初始压比为2.86，最终稳态压比为3.62。整个过程机组压比＜4，满足供气压缩机组并网安全要求。在阶段1，关闭回流阀导致机组压比升高可以通过开启入口阀抑制。阶段1 结束后，机组仿真稳态压比为2.72，实验稳态压比为2.87。阶段2 机组排空阀关闭，入口阀和供气阀开度增大，压比波动出现2 次先下降再升高的过程。第1 次是由于排空阀、入口阀与供气阀通流能力不同，开度变化对机组压比的影响不同，开启入口阀与供气阀对压比的影响强于关闭排空阀，导致机组压比先下降再升高；第2 次是排空阀完全关闭，入口阀与供气阀完全开启后，供气总管内背压建立的过程，机组压缩机后压力随着供气总管内压力升高而升高。

压缩机压比在阀门动作时误差大于稳态时的误差，尤其在阶段1 回流阀动作时，压比相对误差大于其他时刻，但压比变化趋势一致。阶段2仿真结果压比与实验结果误差小于阶段1。阶段1 压比最大误差达到0.51，相对误差为21.49%，而阶段2 压比最大误差为0.50，相对误差为14.28%。仿真结果与实验压比平均误差为0.092，平均相对误差为3.23%。

仿真结果与实验存在误差。对于供气压缩机组这类复杂的热力系统，误差来源包括：

1） 仿真结果与实验主要误差出现在阀门动作过程中，而阀门阀位不变时仿真结果与实验符合良好，说明以节流孔板模型作为阀门模型时，未充分考虑阀门的阀位变化带来的通流能力变化的影响，且对于各个阀门，误差大小与阀门开度负相关，在小开度时误差大于大开度时。

2） 稳态工况出现误差的原因主要是阀门模型中使用部分参数通过CFD 仿真结果拟合获得，其精度与三维模型建模精度以及CFD 仿真精度相关，通过提高CFD 建模与计算的精度能够减小阀门流量的误差；压缩机模型流量主要由性能曲线决定，受限于实验条件，测量压缩机流量困难，测量的工况点精度低，且工况点数量不足，导致性能曲线存在误差，可通过压缩机的CFD 仿真获取更多压缩机工况点来提高压缩机模型的精度。

3） 由于实验所用供气压缩机组中阀门为非伺服阀，阀门动作精度低，且调节过程中存在不可控因素，实际阀位与仿真阀位存在差异，也导致了仿真结果与实验结果的误差。

4 结 论

本文针对目前国内试车台供气压缩机组主要依靠人工操作并网的问题，设计了基于规则的专家系统，并在MATLAB/Simulink 平台搭建了动态仿真模型，进行了并网控制仿真，并基于仿真结果进行了供气压缩机组并网控制实验，主要结论如下：

1） 本文建立的供气压缩机组动态模型能够进行机组并网控制仿真，仿真结果中阀门控制信号直接应用于目标机组，顺利完成供气压缩机组并网工作，并网过程中机组最大压比为3.69，最小压比为2.27，满足机组安全要求。供气压缩机组动态模型仿真结果压比与实验中变化趋势一致。实验中，并网完成后供气压缩机组压缩机入口压力为93.42 kPa，压缩机出口压力为338 kPa。

2） 通过该模型进行并网仿真结果可靠，本文所设计的专家系统能够完成该供气压缩机组的并网控制工作。并网过程分为2 个阶段，阶段1耗时＜100 s，阶段2 耗时＜300 s。

3） 供气压缩机组并网过程中阶段1 压缩机入口压力最大误差为8.18 kPa，压缩机出口压力最大误差为2.40 kPa，压比最大误差为0.51；阶段2 压缩机入口压力最大误差为8.87 kPa，压缩机出口压力最大误差为20.49 kPa，压比最大误差为0.50。

4） 供气压缩机组模型的仿真结果与实验结果对比，误差主要出现在入口阀小开度的情况下进行连续动作时，尤其是在供气压缩机组回流状态转节流状态时。整个并网过程压缩机前压力平均相对误差为3.12%，压缩机后压力平均相对误差为0.44%，压比平均相对误差为3.23%。