基于故障注入模型的电传飞控系统安全性分析
荘露,陆中,*,宋海靖,董力,吴雨婷,周伽
1.南京航空航天大学 民航学院,南京 211106
2.中国飞行试验研究院 可靠性研究中心,西安 710089
3.中国航空无线电电子研究所 民机系统部,上海 200241
4.东方航空江苏有限公司 飞机维修部,南京 211106
现代大型民用飞机的电传飞控(Fly-by-Wire, FBW)系统是由机械、电气、电子、液压等部件组成的高集成复杂系统,具有飞行姿态控制、颤振抑制、俯仰轴配平、飞机增稳和升阻控制等重要功能。飞行姿态控制、颤振抑制等功能的丧失、故障或非指令性工作会对飞机、机组和乘客的安全产生严重影响,导致灾难性的失效后果。
系统安全性分析既是飞机研制过程中开展安全性设计、提高飞机系统安全性的主要手段,也是适航审定过程中针对《运输类飞机适航标准》[1]“设备、系统及安装”等条款开展符合性验证的重要方法。目前,对民用飞机系统开展安全性分析主要使用功能危害性评估(Functional Hazard Assessment, FHA)、故障模式与影响分析(Failure Mode and Effect Analysis, FMEA)和故障树分析(Fault Tree Analysis, FTA)等方法[2-3]。在传统的安全性分析过程中,这些方法主观性强,过于依赖分析人员的工程经验,当分析人员对设计方案理解存在偏差时,容易导致分析结果的不完整性和不一致性。同时,这些方法的自动化程度不高,通常需要分析人员手工来完成,飞机系统的研制是一个不断更新迭代的过程,这将导致传统的安全性分析工作异常烦琐。
基于模型的安全性分析(Model-Based Safety Analysis, MBSA)是一类通过将基于模型的开发过程与安全性分析技术相结合以实现自动化或半自动化安全分析的理论或方法[4-5]。在基于模型的开发过程中,各种开发活动(如仿真、验证和测试等)都在系统模型上进行。在该模型基础上,自动注入相应的故障模式,根据模型的响应分析故障影响,确定故障的传播路径或故障之间的逻辑关系,能够实现安全性分析的自动化。同时,安全性分析的输出由系统模型自动生成,从而避免了对分析人员工程经验的依赖。
近20 年来,MBSA 方法已经成为系统安全性建模与分析领域的热点。当前,MBSA 方法总体上可分为体系结构建模方法、有限状态机方法和动力学模型方法3 类。体系结构建模方法利用UML[6]、SysML[7]、AADL[8-9]和AltaRica[10-11]等体系结构建模语言建立系统的形式化模型,在此基础上确定系统各层级故障之间的逻辑关系或故障传播路径,从而自动生成故障树、事件树等安全性分析工具。有限状态机方法通过描述系统状态以及状态之间的变迁关系来对系统进行建模,通过线性时态逻辑或分支时态逻辑来表示系统的安全性需求,并利用模型检测方法来验证能否满足安全性需求,典型的有限状态机建模方法包括Petri 网[12-14]、Stateflow[15]、NuSMV[16-17]等。动力学模型方法利用对象的微分方程、传递函数或状态方程等数学模型来构建仿真模型,能够反映系统的动力学特性,典型的动力学建模工具包括Simulink[18-20]、Modelica[21]等。
对于FBW 系统而言,无论是飞控计算机的控制律、传感器和执行机构的输入输出模型,还是飞机本身的飞行动力学模型,都是通过微分方程、传递函数或状态方程来表示的。这些模型和相关参数可以通过风洞试验、CFD 模拟、系统辨识等方法获得。这些模型和相关参数同样也是在地面构建铁鸟试验台的先决条件,在设计中,也将根据计算机仿真、铁鸟试验、飞行试验的结果对模型和相关参数进行修正。本文将基于FBW 系统的数学模型,使用Simulink 分别构建FBW 系统的名义模型(即无故障模型)和拓展模型(即带故障模型),利用单故障注入后的系统响应提出故障影响分析方法,以支持FMEA 的开展,基于状态遍历实现组合故障注入,并利用组合故障注入后的系统响应提出FTA 方法。根据安全性分析的结果,可以对设计进行修正。这样有助于在系统的研发迭代中,实时获取系统模型和参数的变化对系统安全性的影响,使得安全性分析成为系统开发过程的一部分,避免在安全性分析和系统开发过程中存在“两张皮”的问题。最后结合某横侧向FBW 系统给出应用案例。
1 基于Simulink 的电传飞控系统建模
系统的形式化模型是开展MBSA 的基础,本节以某FBW 系统的横侧向控制系统为对象,利用Simulink 工具分别建立系统的名义模型和拓展模型,基于拓展模型实施故障注入,监控仿真系统在不同故障模式下的响应并分析故障影响。其中,名义模型可由Simulink 模块直接搭建,拓展模型则需要在名义模型的基础上融合部件故障模式的Simulink 模型进行构建。
1. 1 某横侧向FBW 系统
该FBW 系统的横侧向飞控系统由飞控计算机子系统、执行机构子系统、传感器子系统以及副翼、方向舵等舵面组成,以实现飞机的滚转和偏航控制,系统架构如图1 所示[22-23]。
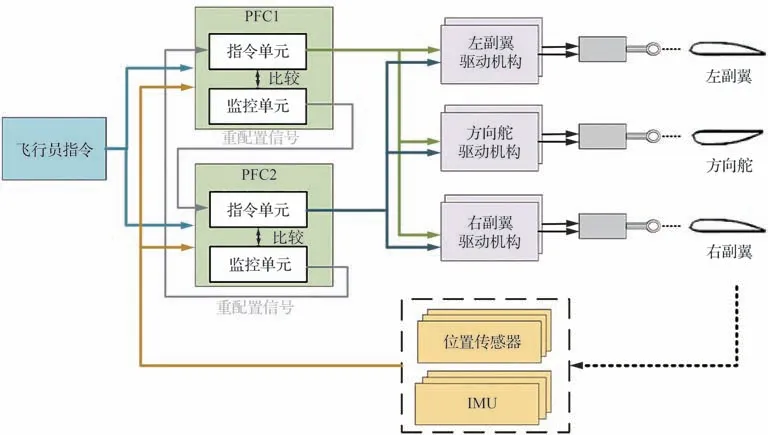
图1 某横侧向FBW 系统架构Fig. 1 Architecture of lateral-directional FBW system
飞控计算机子系统为双冗余架构,由2 台相同的主飞行计算机(Primary Flight Computer,PFC)组成,每个PFC 包含1 个指令单元和1 个监控单元。指令单元根据输入的飞行状态、飞行员指令等数据,计算控制律并输出舵面偏转指令。监控单元也进行控制律的计算,但其计算结果用于与指令单元进行比较,当2 个单元的计算差值超过一定的阈值时,监控单元会抑制舵面偏转指令的输出,并将故障信息发送给另一个PFC 以重新配置控制命令。
驱动机构子系统由左副翼驱动机构(Left Aileron Actuation, LAA)、右副翼驱动机构(Right Aileron Actuation, RAA)和方向舵驱动机构(Rudder Actuation, RA)组成。驱动机构均为双冗余架构,每个驱动机构与合成器连接,用于合成2 个驱动机构的信号。传感器子系统包括3 个舵面的位置传感器和惯性测量单元(Inertial Measurement Unit, IMU),它们均为三冗余架构。
1. 2 横侧向FBW 系统名义模型
文献[23]给出了以微分方程、传递函数或状态方程等形式表示的该横侧向FBW 系统各部件的数学模型,利用Simulink 模块库可构建相应部件的模型,将部件模型综合后即为FBW 系统的名义模型,如图2 所示。

图2 基于Simulink 的横侧向FBW 系统名义模型Fig. 2 Simulink-based nominal model of lateral-directional FBW system
1. 3 部件故障模式建模与注入
该横侧向飞控系统组成部件共有无响应、随机输出、延迟、卡滞、舵面松浮、增益改变和信号漂移共7 种故障模式[24]。借助Simulink 中的Switch及相关模块,可以对部件故障模式进行建模,通过控制信号端口,可以实现正常信号和故障信号的切换。表1 给出了各故障模式的描述、数学模型以及建模时使用的Simulink 模块。表中,y(t)表示故障信号;yr(t)表示输入的正常信号;min 和max 表示设定的生成随机数的下界和上界;t0表示设定的延迟时间量;yr(t′)表示上一时间步的正常信号;yi表示第i个飞行状态(包括爬升、巡航、下降)舵面松浮的角度;a表示设定的信号放大或缩小的倍数;y0表示设定的信号偏移量。

表1 常见故障模式及说明Table 1 Typical fault modes and descriptions
假设某部件具有表1 给出的7 种故障模式,则使用Simulink 的“Multiport Switch”模块构建的部件故障模型如图3 所示。图3 中部件共有8 种状态,包括“正常”状态以及表1 中7 种故障模式对应的故障状态,这8 种状态分别对应控制信号0、1、2、3、4、5、6、7。通过选择控制信号值,可在名义模型中注入不同的故障模式。
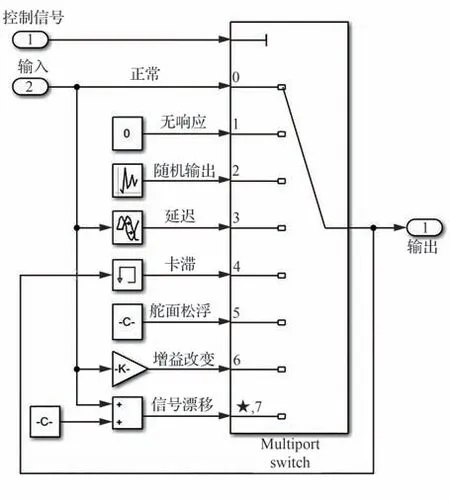
图3 基于Simulink 的部件故障模型Fig. 3 Simulink-based component extended model
1. 4 横侧向飞控系统拓展模型
将部件的无故障模型与故障模型相融合,即可建立部件的拓展模型,将所有部件的拓展模型连接在一起,即可建立系统的拓展模型[25]。
该FBW 系统的25 个组成部件的序号、名称以及故障模式序号如表2 所示,其中故障模式序号与表1 给出的7 种故障模式的序号对应。
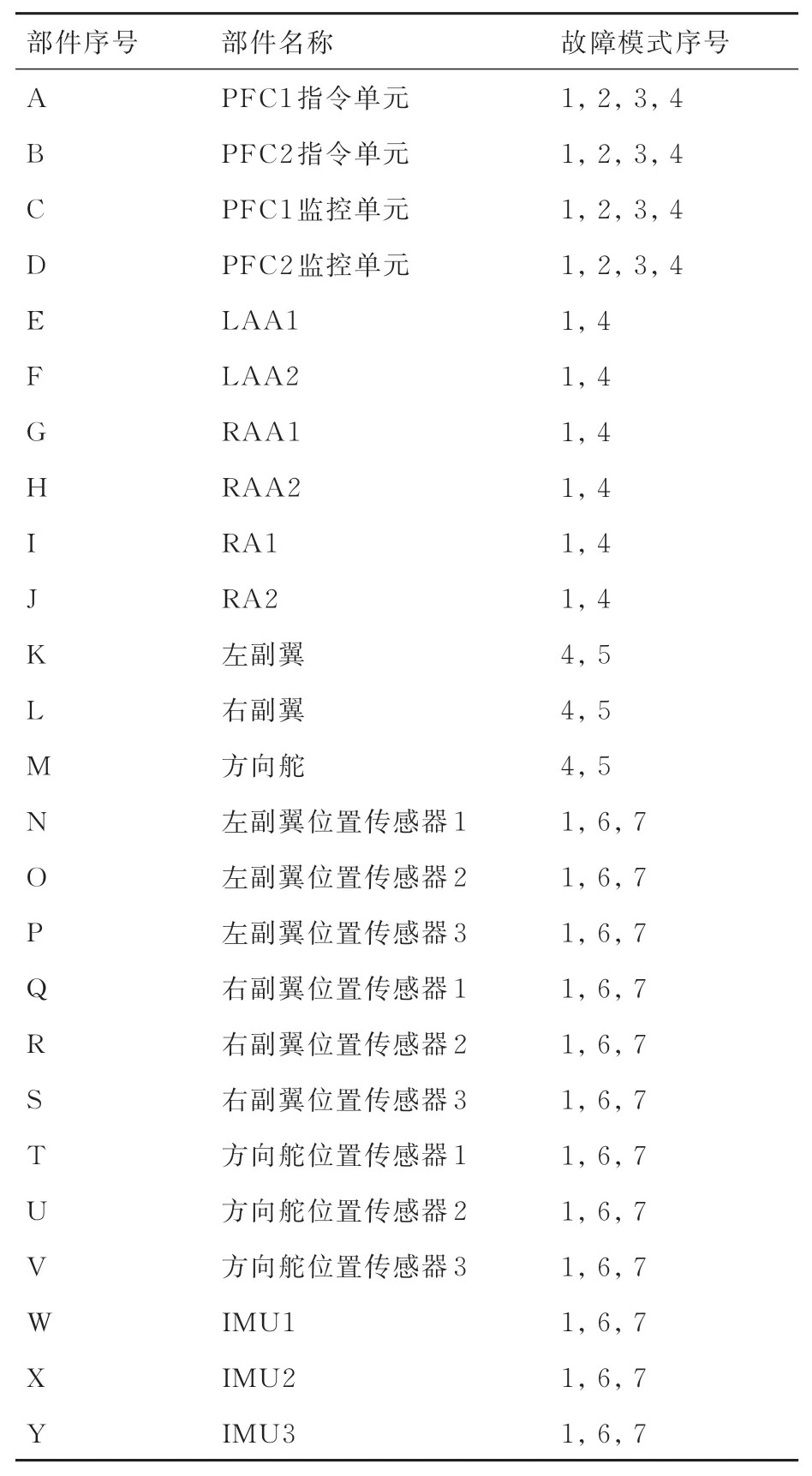
表2 各个部件的故障模式Table 2 Failure modes of each component
图4 以PFC 为例给出了部件的拓展模型,图4中左侧为PFC 的名义模型,右侧为PFC 的故障模型,该故障模型包括“正常”状态以及“无响应”“随机输出”“延迟”“卡滞”4 种故障状态,这5 种状态对应的控制信号值分别为0、1、2、3、4。
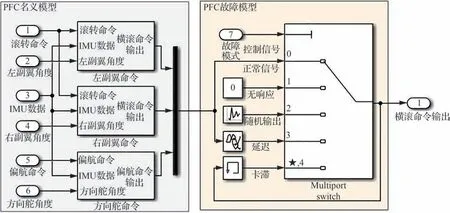
图4 基于Simulink 的PFC 的拓展模型Fig. 4 Simulink-based extended model of PFC
针对图2 中每个部件构建拓展模型,并将其连接在一起,可建立该横侧向FBW 系统的拓展模型,如图5 所示。

图5 基于Simulink 的横侧向FBW 系统拓展模型Fig. 5 Simulink-based extended model of lateral-directional FBW system
2 基于单故障注入的故障影响
在飞机系统安全性分析中,FMEA 是一种识别部件的所有故障模式并分析其对更高层次影响的安全性分析方法。FMEA 通常用于分析单个故障模式对飞机或系统的影响,以利于发现系统设计的薄弱环节。其中故障影响的确定是FMEA 的重要环节,传统的FMEA 方法主要依赖分析人员的经验来识别故障影响,本研究将通过故障注入后的系统性能响应来确定故障影响。
2. 1 系统性能指标与阈值
FHA 确定的系统顶层失效状态(Failure Condition, FC)是否会发生,是分析故障模式“最终影响”的主要依据。为每个FC 定义性能指标和阈值,并监控注入故障后的系统响应。当飞机处于安全状态时,各性能指标的响应应限制在可接受的范围内,一旦性能指标超出了阈值,系统顶层FC 发生。
图1 所示的横侧向FBW 系统由FHA 确定的顶层FC 包括“导致不安全飞行路径的滚转功能丧失”和“导致不安全飞行路径的滚转振荡”。
“导致不安全飞行路径的滚转功能丧失”的性能指标为侧滑角β、滚转率pr、偏航率rr和滚转角ϕ。其性能要求定义为
式中:yi(t)是第i个性能指标;yir(t)是第i个性能指标的参考值,即系统在无故障情况下第i个性能指标的取值;ri是第i个性能指标的阈值;β、pr、rr和ϕ的阈值分别为0.15 rad、0.45 rad/s、0.45 rad/s 和0.15 rad。
“导致不安全飞行路径的滚转振荡”的性能指标为飞机的滚转角ϕ,阈值定义为20 s 内通过0 rad 的频率大于1 次/s 的数量不超过10。
对于故障的“局部影响”或“高层次影响”,可根据相应层级的系统或子系统的输出响应,采用与上述类似的方法来分析。例如,要分析图5 中PFC1 指令单元的故障模式的影响,可通过故障注入后PFC1 的输出参数“左右横滚命令输出”和“偏航命令输出”的响应来进行判别。
2. 2 典型故障模式的故障影响
以图1 所示的横侧向FBW 系统为例,其输入的滚转指令为0.2 rad、0.1 Hz 的方波,系统在正常状态时的响应如图6 所示。
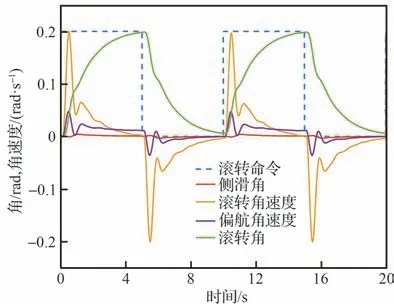
图6 无故障状态下横侧向FBW 系统的性能响应Fig. 6 Performance responses of lateral-directional FBW system without fault injection
注入“左/右副翼-舵面松浮”故障后,系统的性能响应如图7 所示。此时,滚转角ϕ显然超过了规定的阈值0.15 rad,因此可判断“左/右副翼-舵面松浮”故障的最终影响为“导致不安全飞行路径的滚转功能丧失”。
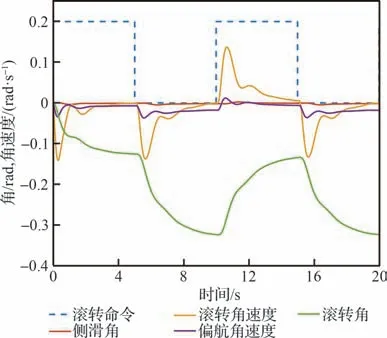
图7 左/右副翼松浮时横侧向FBW 系统的性能响应Fig. 7 Performance responses of lateral-directional FBW system with left/right aileron trailing
注入“方向舵-舵面松浮”故障后,系统的性能响应如图8 所示。此时,滚转角ϕ超过了规定的阈值0.15 rad,且发生了微小振荡,但其振荡频率没有超过阈值(即20 s 内通过0 rad 的频率大于1 次/s 的数量不超过10),因此可判断“方向舵-舵面松浮”故障的最终影响仅仅为“导致不安全飞行路径的滚转功能丧失”。

图8 方向舵松浮时横侧向FBW 系统的性能响应Fig. 8 Performance responses of lateral-directional FBW system with rudder trailing
完成所有单故障注入发现,所有单故障均不会“导致不安全飞行路径的滚转振荡”,则该顶层FC 不会被单故障触发。
3 基于故障遍历的故障树
FTA 是一种组合故障分析方法,能够确定导致顶层FC 的故障原因组合,并计算顶事件发生概率。FMEA 不能分析组合故障的影响,上述分析中尽管所有单故障都不会“导致不安全飞行路径的滚转振荡”,但是当“PFC 指令单元-无响应”和“PFC 监控单元-无响应”2 个故障模式同时发生将导致该FC 发生,如图9 所示。
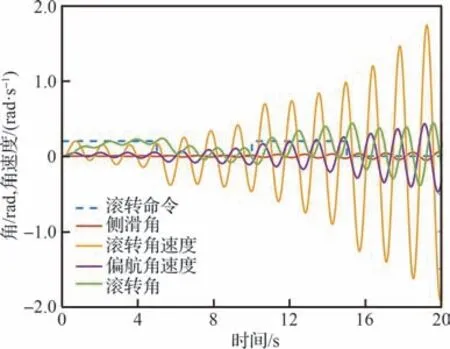
图9 PFC 指令和监控单元无响应时横侧向FBW 系统的性能响应Fig. 9 Performance responses of lateral-directional FBW system with both PFC command and monitor unit omission
本节提出了一种基于故障遍历的FTA 方法,首先利用递归法得到了系统的所有故障组合;其次提出了故障组合的约简方法以提高分析效率;然后通过状态遍历将故障组合注入到名义模型中,并根据系统响应来判断是否会导致顶层FC 的发生,即确定故障组合是否是割集;最后可利用最小割集(Minimal Cut Set, MCS)计算出响应的FC 的发生概率。所提出的方法利用组合故障的性能响应来确定导致顶层FC 的MCS,同样避免了对分析人员经验的依赖。
3. 1 基于递归法的故障组合确定
要使用状态遍历进行故障注入,首先必须得到所有的故障组合。假设系统由m个部件组成,每个部件的故障模式数用向量N来表示:
式中:ni表示第i个部件共具有ni种故障模式。
每个故障组合用向量C来表示:
式中:ci=0 表示第i个部件无故障;ci=j(j=1,2,…,ni)表示第i个部件的第j种故障模式发生。假设一个故障组合中有q(q=1,2,…,m)个部件故障,则向量C中有q个非零元素。
通过递归法得到的q个部件故障的所有故障组合的伪代码描述如算法1 所示。
3. 2 故障组合的约简
为减少需遍历的故障组合数,提高安全性分析效率,可先对已生成的故障组合进行约简。故障组合的约简有2 种方法:

算法1 故障组合的生成Input: 故障部件的个数q、部件的总个数m、部件的故障模式数向量N Output: q 个部件故障的所有故障组合Com 1. void GetCombination(q, m, N) ∥得到q 个部件故障的所有故障组合2. C←[0]1×m ∥向量C 表示一个故障组合,C 为全零矩阵时表示系统正常3. i←1 ∥ i 为部件编号4. k←0 ∥ k 表示故障部件编号,即向量C 中的第k 个非零元素5. Recursive(i, k)6. End 7. void Recursive(i, k) ∥递归函数8. if i≤m then 9. k←k+1 10. for x=i:m 11. for j=1:N(x)12. C(x)=j 13. if k=q then 14. 当前向量C为一个故障组合,保存入向量组Com 15. else 16. Recursive(x+1, k)17. End if 18. C(x)=0 19. End for 20. End for 21. else 22. return 23. End if 24. End
1)若某一故障组合的子集是MCS,则该故障组合可舍弃,不用再进行故障注入。即在遍历q个元素的故障组合时,若该故障组合包含MCS(阶数小于q),则该故障组合无须考虑,因为其已经在之前的迭代中考虑过。
2)利用相似余度,余度架构中的相似部件的故障在故障组合中不重复考虑。在生成故障组合时,部件的冗余被视作几个不同的部件(如PFC、驱动机构、传感器),包括单个故障、多个故障等所有故障方式都被考虑在内。对于非相似冗余,可以直接遍历;对于相似冗余,其对故障的响应也是相同的,可先对这部分故障组合进行约简。如该FBW 的PFC 采用了2×2 余度结构,使用了2 个完全相同的PFC,每个PFC 中有2 个相似的支路,分别为指令单元和监控单元;2 个完全相同的驱动机构分别与2 个PFC 单独连接(如图2 所示)。由于部件A、B、C、D 均为相似的指令或监控单元,因此与部件组合{A, E, G, I}、{C, E, G,I}、{B, F, H, J}和{D, F, H, J}相关的故障组合注入系统后的响应是相同的,因此仅需要保留一个作为代表,本文称之为故障组合代表。对故障组合进行约简的伪代码如算法2 所示。

算法2 故障组合的约简Input: q 个部件故障的所有故障组合Com Output: 约简后的剩下的q 个部件故障的故障组合SimpleCom 1. void Simplify(Com)2. n←size(Com,1) ∥读取剩余q 个部件故障的故障组合的个数3. for i=1:n 4. if 包含q-1 阶及以下MCS then 5. Com(i,:)清零6. End if 7. if 有相似余度故障 then 8. 将Com(i,:)中对应元素替换为故障组合代表9. End if 10. End for 11. 去除故障组合中的重复行和全零行,得到SimpleCom 12. End
3. 3 基于状态遍历的安全性分析方法
将遍历约简后的故障组合注入系统模型并分析系统响应,可以得到导致系统顶层FC 发生的MCS,即确定系统失效的原因,以便于改进系统设计。并且,利用故障模式的故障率数据还可以根据MCS 计算顶层FC 的概率。
基于状态遍历识别MCS 并计算系统顶层FC 概率的伪代码描述如算法3 所示。
4 实例分析和讨论
本节基于图1 所示的横侧向FBW 系统给出了FMEA 与FTA 分析实例。
4. 1 基于单故障注入的FMEA 实例
考虑到该横侧向FBW 系统的功能及组成特点,可将系统划分为PFC 子系统、驱动机构、传感器子系统和控制面4 个部分。每个子系统都由若干部件组成,各部件的故障模式如表2 所示,部件故障模式的故障率如表3 所示,其层次分解图如图10 所示。
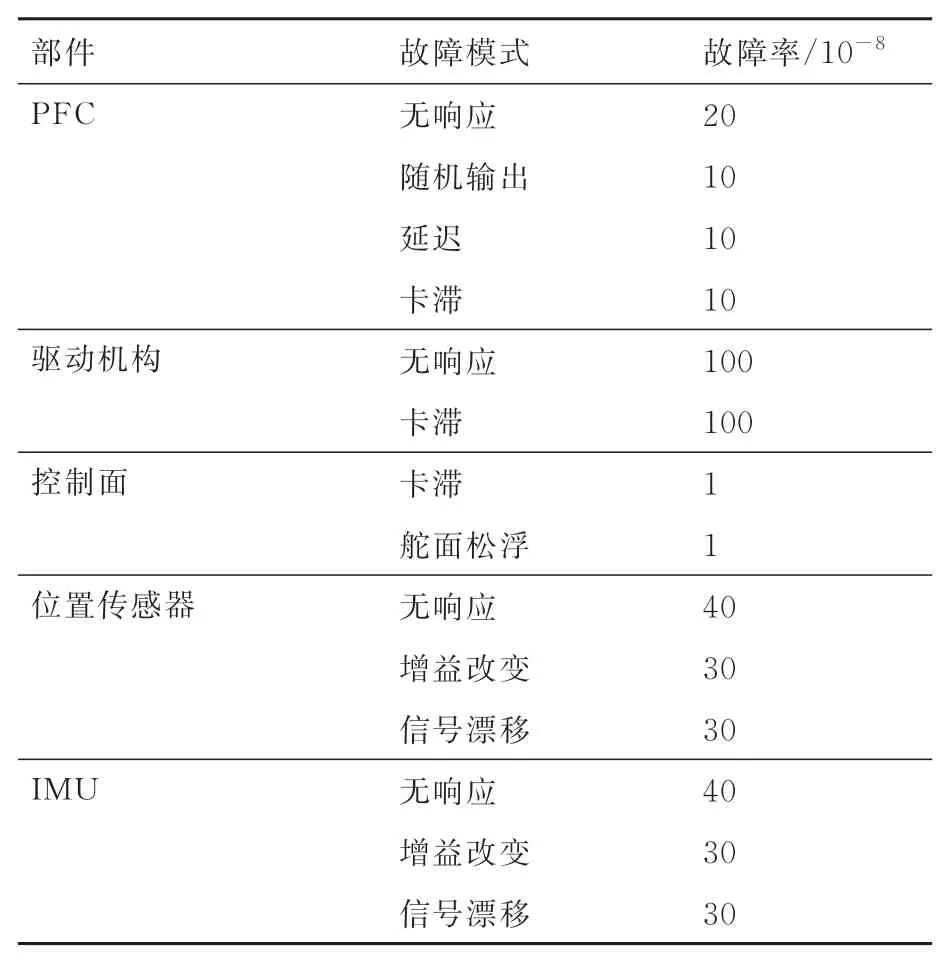
表3 部件故障模式的故障率Table 3 Failure rate of failure modes of components
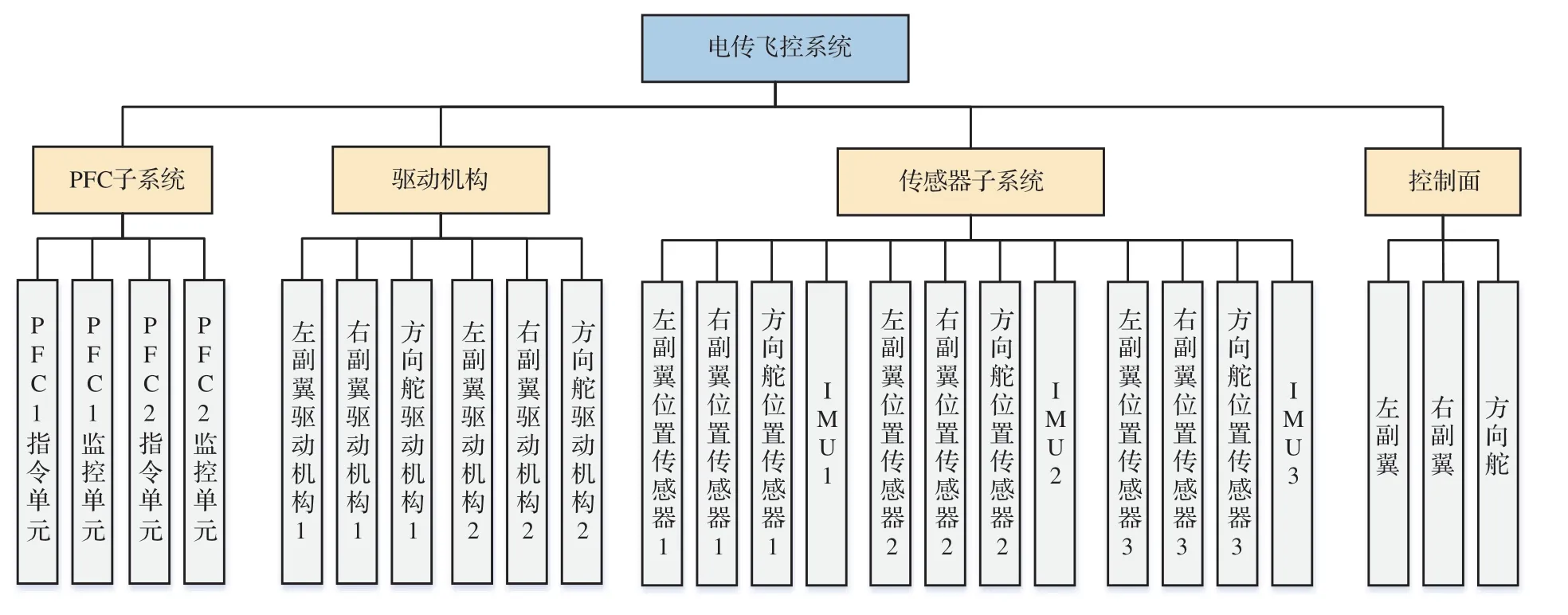
图10 横侧向FBW 系统的层次分解图Fig. 10 Hierarchical decomposition diagram of lateral-directional FBW system
分析每类部件的故障模式,给出其对当前层级、高一层的子系统级、系统级的影响,确定故障检测方法,即完成了FMEA。

算法3 基于状态遍历的MCS 识别与FC 概率求解Input: 故障部件的个数q、部件的总个数m、部件的故障模式数向量N Output: 系统的MCS 和顶层FC 的失效概率1. void StateTraversal()2. for q=1:m 3. l←1 4. GetCombination(q, m, N) ∥ 调用算法1 得到q 个部件故障的所有故障组合5. Simplify(Com) ∥调用算法2 约简故障组合6. n←size(SimpleCom,1) ∥读取剩余q 个部件故障的故障组合的个数7. for l=1:n 8. 将第l 个故障组合注入系统模型9. 运行拓展模型10. if 导致系统顶层FC 发生 then 11. 记录当前故障组合为顶层FC 的一个q 阶MCS 12. End if 13. End for 14. End for 15. 根据系统顶层FC 的所有MCS 计算其失效概率16. End
以PFC 子系统中的PFC1 指令单元为分析对象,其功能为“获取飞行员指令和飞机姿态信息,经控制律解算,指令驱动机构动作”。通过分析PFC1 指令单元的4 种故障模式及其影响,得到的FMEA 表如表4 所示。
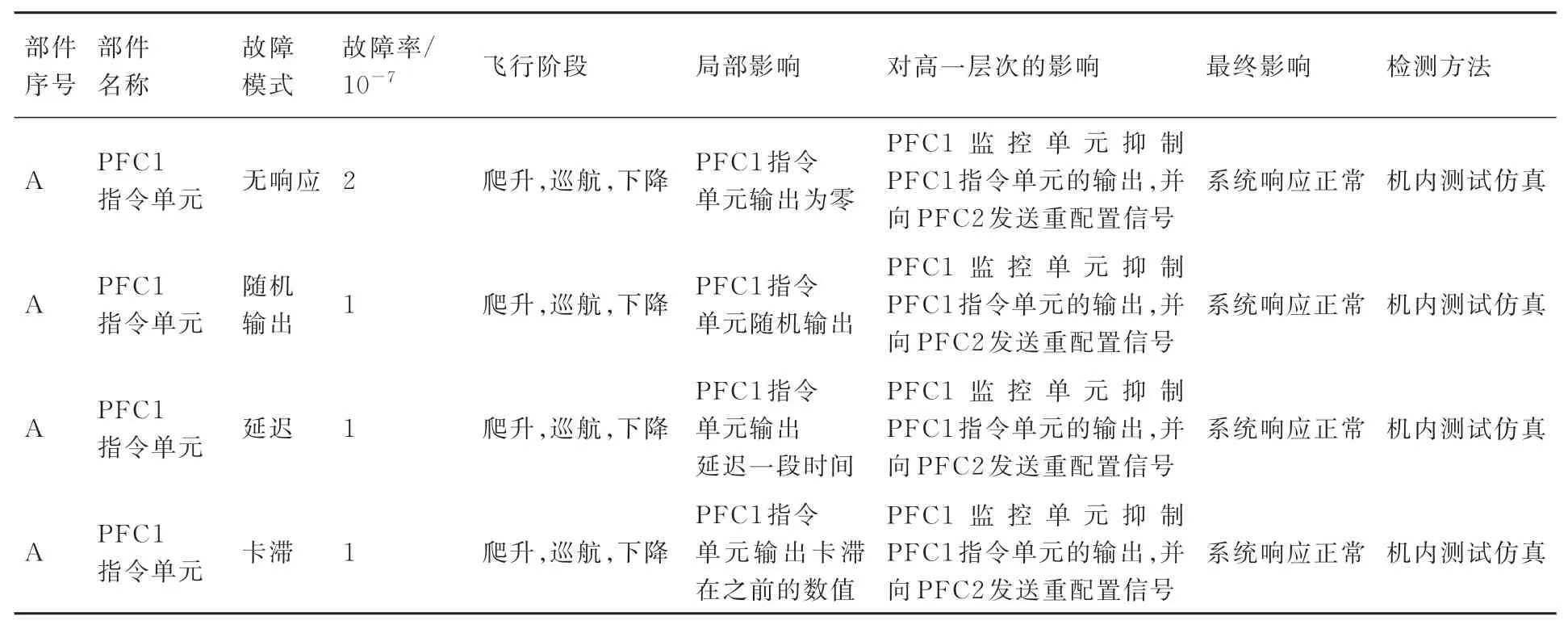
表4 PFC1 指令单元部件级FMEA 表Table 4 Piece-part FMEA worksheet for command unit of PFC1
以控制面子系统中的左副翼为分析对象,其功能为“为飞机提供滚转控制”。通过分析左副翼的2 种故障模式及其影响,得到的FMEA 表如表5 所示。

表5 左副翼部件级FMEA 表Table 5 Piece-part FMEA worksheet for left aileron
4. 2 基于状态遍历的FTA 实例
通过状态遍历法,分别得到该横侧向FBW系统顶层FC“导致不安全飞行路径的滚转功能丧失”的MCS 共3 293 个,对等价的MCS 约简后剩余215 个,其中一阶3 个,二阶42 个,三阶104个,四阶及以上66 个。
顶层FC“导致不安全飞行路径的滚转振荡”的MCS 共1 128 个,对等价的MCS 进行约简后剩余109 个,其中一阶0 个,二阶6 个,三阶60 个,四阶及以上69 个。
(一)有利于生产各环节的全程监控,保障畜产品质量安全 随着社会经济的快速发展,人们消费意识和水平的不断提高,消费者对所需食品的质量要求越来越高。而分散的小规模生产,很难有效对其生产的各个环节进行有效监控,产品质量无法保障,只有标准化规模化发展生猪养殖,才能有利于监管,有效避免有毒、有害、违禁药品、饲料、添加剂、微量元素、矿物质进入畜体,保障畜产品质量安全。
在计算顶事件发生概率时,需要用到基本事件的暴露时间和故障率,由于该横侧向FBW 系统的所有部件在整个航段时间内均在工作且不存在隐性故障,因此故障树每一基本事件的暴露时间均取平均航段时间。各部件故障模式的故障率见表3,假设该飞机的平均航段时间为10 h,根据求得的MCS 可计算得到“导致不安全飞行路径的滚转功能丧失”每航段时间内的发生概率为3.002 661×10-7,每飞行小时发生概率为3.002 7×10-8;“导致不安全飞行路径的滚转振荡”每航段时间内的发生概率为1.140 6×10-10,每飞行小时发生概率为1.140 6×10-11。
4. 3 分析与验证
针对该系统,文献[26]提出了利用经典的马尔可夫分析方法(Markov Analysis, MA)求失效概率上下限的近似方法求解失效状态发生概率。MA 的主要步骤为:① 注入故障模式,运行系统拓展模型,确定系统的各个状态(正常、失效),绘制出系统的状态转移图;② 依据系统状态转移图,构建相应的状态转移矩阵以及用于求解飞行控制系统状态概率的微分方程组;③ 通过求解微分方程组能够得出系统在某一时刻处于各个状态的概率,进而求解系统失效概率。
该横侧向FBW 系统“导致不安全飞行路径的滚转功能丧失”的MA 模型如图11 所示。
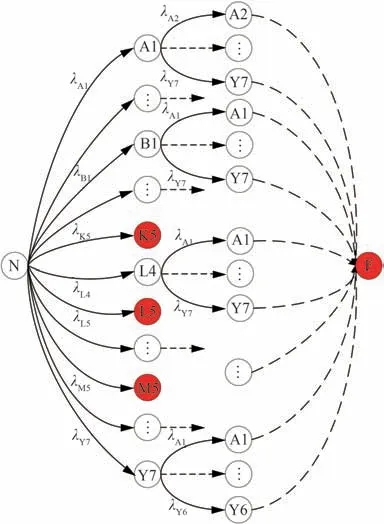
图11 滚转功能丧失的MA 模型Fig. 11 MA model for loss of roll control
图11 中,红色圆表示系统的吸收状态;标号为N 的圆表示系统的正常状态;标号为字母与数字组合的圆表示系统的中间状态。以标号为A1的圆为例,其表示部件A 的故障模式1 发生,λA1为部件A 的故障模式1 的故障率。通过求解马尔可夫过程的Fokker-Planck 方程可以计算出顶层FC 发生的概率。
为了简化MA 过程,可以通过截断MA 模型来减少状态数[27],截断后的MA 模型包含的状态数将大幅减少,其减小程度取决于截断水平的高低。图11 取3 级截断后的MA 状态转移图如图12 所示,图12 中除了完全失效状态T 外,其他包含3 个故障以上的状态将不再考虑。
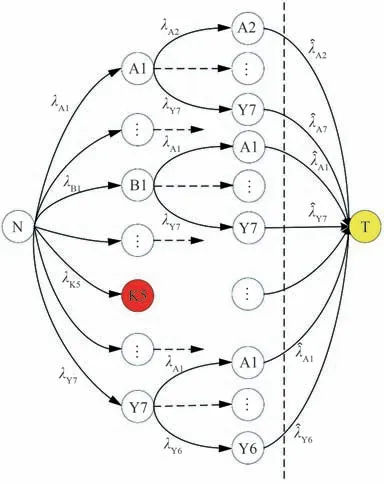
图12 3 级截断下的状态转移图Fig. 12 State transition diagram at third truncation level
图12 中相应的故障率可通过式(4)求得
MA 模型截断后,无法得到系统的MCS 和顶层FC 发生的精确概率,但可以计算顶层FC 发生的概率的上下界[25,27]。当取截断等级为3 时,求得的2 个顶层FC 的发生概率的上下界见表6。

表6 不同方法得到的顶层FC 发生概率Table 6 Probability of top-level FC occurrence calculated by different methods
此外,还能够通过蒙特卡罗仿真的方法近似求解该FBW 系统失效状态的发生概率[25]。蒙特卡罗仿真的具体方法为:将每个部件故障模式的故障时间用随机数表示,将这些数字从小到大排序,按照故障注入方法逐个注入发生时的失效模式。当响应不满足安全要求时,将终止一次模拟,得到不安全状态下的时间样本。根据几个时间样本,可以得到不安全条件下的时间概率分布。这样就可以计算出不同时间点的不安全状况发生的概率。通过蒙特卡罗仿真计算出的平均航段时间内发生不安全状况的概率见表6。
由此可见,通过本文方法计算得到的概率位于MA 方法得到的概率上下界之间,与蒙特卡罗仿真的结果近似,说明了本文方法的准确性。
此外,随着设计的更改,MA 模型需要重新手动构建,而本文方法可以根据修改后的系统模型,自动更新安全性分析结果,避免了烦琐的建模工作。蒙特卡罗仿真方法虽然节约了分析时间,但其是一种随机方法,无法得到精确的失效概率,也无法得到失效状态的MCS。
5 结 论
本文提出了基于Simulink 的FBW 系统安全性分析方法。通过注入单个故障和故障组合遍历,实现了FMEA 和FTA 的自动化。与传统的安全性分析方法相比,本文方法具有以下优点:
1)提出了一种MBSA 方法,基于Simulink建立了FBW 系统名义模型和拓展模型,能够自动分析FMEA 的故障影响、确定FTA 的MCS 并计算顶层FC 的发生概率。
2)利用故障注入后的系统的性能响应来确定部件故障或故障组合对系统安全性的影响。与传统的安全性分析方法相比,系统失效的确定不依赖于分析人员的技术和经验,更具有客观性。
3)当系统设计方案更改时,利用更改后的拓展模型能够自动更新安全性分析结果,不需要重新构建安全性分析模型(如FTA、MA 或依赖图分析),从而避免了手动重新建模的烦琐工作。

