基于Transformer 模型的空战飞行器轨迹预测误差补偿方法
张百川,毕文豪,张安,毛泽铭,杨咪
西北工业大学 航空学院,西安 710072
空战中的轨迹预测是根据目标飞行器的运动特性和历史运动轨迹,对未来时刻飞行器可能到达的位置进行合理计算的过程。在信息化战场环境下的空战中,准确的轨迹预测结果能够为战术决策提供可靠的数据支撑。由包以德(Observation, Orientation, Decision and Action,OODA)循环理论可知,空战中取得优势的关键在于比对手更快地形成连续的OODA 循环[1],从而达到“料敌于先,先发制人”的目的。优秀的轨迹预测能力能够使攻击机更快地完成“观察”过程,提前进入“判断”阶段,在空战中迅速建立优势。因此,研究目标飞行器的轨迹预测算法对取得空中优势具有重要意义。
为了提高目标飞行器的飞行轨迹预测精度,国内外学者针对上述问题进行了大量研究。一部分学者对轨迹预测算法进行了深入优化,其研究成果可大致分为2 类[2]。
第1 类是知识驱动的预测算法,这类算法需要结合预测目标的运动模型,对未来时刻目标的运动状态进行最优估计,适用于有限维度的线性和非线性的目标时空运动轨迹[3-5]。例如,文献[6]针对长时预测问题,提出了一种基于高斯混合模型(Gaussian Mixture Models,GMMs)的车辆轨迹预测算法。文献[7]通过分析临近空间高超声速目标的机动特性,建立了参数化的目标机动模型,并基于机动模型提出了可学习卡尔曼滤波轨迹预测方法。然而,上述知识驱动的轨迹预测算法在实际应用中仍存在一定的局限性。首先,目标飞行器的动力学方程或运动方程参数通常需要结合计算流体力学或风洞实验获得,而上述参数在实际的空战场景中难以获取。其次,机载雷达难以准确地捕获到目标飞行器的姿态信息,在飞行器运动模型的基础上所计算出的未来轨迹信息的可信度较低。
第2 类是以深度学习算法为代表的数据驱动的预测算法研究[8-10]。这类算法摆脱了飞行器运动模型的局限,能够结合大量历史数据建立目标机的轨迹预测模型。在更多情况下,循环神经网络(Recurrent Neural Network,RNN)及其衍生模型能够更好地处理序列型预测任务。文献[8]在战场空间栅格中添加了模糊机制,并结合长短时记忆(Long Short-Term Memory,LSTM)网络提出了一种飞行器轨迹预测方法,一定程度上解决了栅格预测模式中边界突变的问题,并同时对飞行器的运动模式加以考虑。文献[9]将轨迹预测问题视为序列对序列的生成问题,通过结合RNN 和混合密度神经网络(Mixture Density Network,MDN)对驾驶员进行分析,对未来时刻轨迹的概率分布进行了计算。文献[11]结合了卷积神经网络(Convolutional Neural Network, CNN) 与LSTM 网络实现了民航飞行器的4-D 轨迹预测。尽管基于RNN 及其衍生模型的方法在轨迹预测任务中取得了较为优秀的表现,但依然存在计算资源消耗大、数据特征损耗严重等问题。除此之外,上述端到端(End To End)的方法由于过于依赖完备的数据集和训练技巧,难以应对序列预测任务中的复杂多变的场景。
基于上述原因,另一部分学者将预测任务拆分成基准值预测和误差补偿2 个阶段。例如文献[12]采用反向传播神经网络(Back Propagation Neural Network,BPNN)对粒子群算法预测的原油价格进行补偿,文献[13]采用基于门控循环单元(Gated Recurrent Unit,GRU)的误差补偿算法实现了对电网中短期电力负荷的预测。文献[14]提出了一种以小波变换为基准,结合超限学习机误差补偿的两阶段风力预测方法。文献[15]提出了一种改进广义误差分布模型,用于计算风电功率预测误差,并通过序列化数据的分析,对误差变化趋势进行描述。上述算法均将误差补偿问题作为序列型数据预测问题进行处理,并利用数据驱动的算法对误差值进行求解。然而随着应用场景逐渐复杂,模型输入的序列数据维度日渐增大,现有的算法暴露出通用性差、特征提取能力弱、补偿精度不足的问题。
Transformer 模型[16]以其强大的特征提取能力,自提出以来便在机器翻译、阅读理解、文本摘要等序列型数据场景中展现出了良好的应用效果。国内外学者也逐步探索Transformer 模型在序列数据预测方面的应用,例如文献[17]在提出了一种基于Transformer 模型的滚动轴承剩余使用寿命预测方法,并在PHM2012 和XJTU-SY数据集上测试了其有效性。文献[18]提出了一种LSTM-Transformer 结构的洋流预测模型,并在NOAA 发布的洋流数据集中进行了验证。文献[19]将多卫星任务规划过程描述为序列生成任务,并提出了基于Transformer 的任务初始方案规划方法,并利用基于随机爬山的约束修正算法对方案进行优化调整。
因此,本文在对现有的轨迹预测算法分析的基础上,结合Transformer 中自注意力机制特征提取能力强、计算复杂度低的特点,提出了一种基于Transformer 模型的预测误差补偿(Transformerbased Prediction Error Compensation,TFPEC)
方法,能够针对现有的各类轨迹预测算法的预测结果,计算出相应的补偿值,以提高轨迹预测精度。本文的主要创新点包括:
1)基于Transformer 结构建立了预测误差补偿模型。针对空战环境中具有高机动运动特性的目标飞行器,结合现有的飞行器轨迹预测算法的特点,建立预测误差补偿模型,以提高现有轨迹预测算法的预测精度。
2)提出了误差补偿系数计算方法。针对目标飞行器的历史轨迹序列,利用傅里叶变换求解其复指数形式的频域表达,对轨迹的高频分量模值特性进行分析,面向目标飞行器的不同运动状态计算误差补偿系数,进一步提高误差补偿方法的性能。
论文组织如下:第1 节构建了目标飞行器轨迹预测误差补偿问题的数学模型;第2 节设计了基于Transformer 的轨迹预测误差补偿方法;第3节在所提出的模型的基础上给出了仿真结果对比和分析;第4 节为本文的总结,并提出下一步的研究方向。
1 轨迹预测误差补偿问题建模
1. 1 问题描述
在空战过程中,定义目标飞行器在t时刻的轨迹序列为P(t),同时给定轨迹预测算法F(P(t)),求取预测误差补偿模型G(P(t);θf),使轨迹预测点与误差补偿值的矢量和与目标下一时刻真实位置的欧式距离最小,即满足下述目标
式中:θf代表误差补偿模型的参数集合;σ(t+1)代表误差补偿系数;p(t+1)代表目标下一时刻的真实位置。定义为给定的轨迹预测算法所计算出的t+1 时刻目标飞行器可能出现的位置基准预测值;为t+1 时刻位置基准预测值所对应的误差补偿值,则目标飞行器轨迹预测问题如图1 所示。
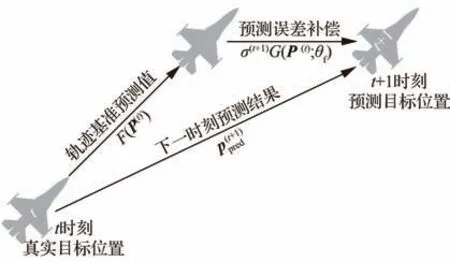
图1 轨迹预测误差补偿问题示意图Fig. 1 Diagram of trajectory prediction error compensation problem
为便于后续研究,本文中对轨迹预测误差补偿问题进行如下假设:
1)目标飞行器轨迹序列中仅包含位置和速度信息,而不包含姿态、推力等机载雷达无法获取的信息。
2)所获取的目标飞行器轨迹为等间隔时间序列,且轨迹中间无丢拍、错拍等问题。
3)在针对目标飞行器的预测过程中,不考虑飞行器与其所在集群中其他单位的交互。
1. 2 参数及决策变量意义
1)p(t)=[x(t),y(t),z(t)]T代表目标飞行器在t时刻北天东坐标系Oxyz下的位置。
3)P(t)=<t,p(t),v(t)>代表目标飞行器在空战过程中t时刻的轨迹点。
7)θf={θTF,θMLP,θFFT}代表轨迹预测算法F(P(t))所对应的误差补偿模型的参数集合,其中θTF、θMLP和θFFT分别代表误差补偿模型中Transformer 参数、多层感知机(Multiple Layer Perceptron,MLP)参数以及误差补偿系数相关参数。
8)Δt代表输入序列的采样间隔,δ代表预测步长。代表预测的飞行器下一时刻位置。
2 飞行器轨迹预测误差补偿方法
本文基于Transformer 模型和离散傅里叶级数设计了轨迹预测误差补偿方法,首先对轨迹序列进行块分割处理,其次利用Transformer编码器捕获序列特征,然后引入MLP 结构计算误差补偿值,最后根据轨迹序列频域上的模值特性来计算误差补偿系数。基于Transformer模型的预测误差补偿方法的具体计算步骤如图2 所示。
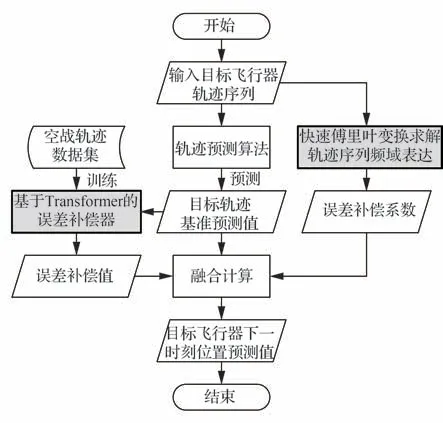
图2 基于Transformer模型的预测误差补偿方法示意图Fig. 2 Diagram of Transformer-based prediction error compensation method
步骤1给定轨迹预测算法以及预测时间间隔,并输入指定长度的目标飞行器轨迹序列,计算目标飞行器下一时刻的轨迹的基准预测值。
步骤2基于Transformer 的误差补偿模型对轨迹预测算法可能产生的误差进行计算,得到基准预测值的误差补偿值。
步骤3针对飞行器轨迹序列的傅里叶级数的模值特性进行研究,求解误差补偿系数,以修正飞行器在平稳机动的过程中所产生的误差补偿过剩的问题。
步骤4综合计算基准预测值、误差补偿值以及误差补偿系数,输出目标飞行器下一时刻可能出现的位置的预测结果。
2. 1 轨迹序列特征提取
本文选取Transformer 模型作为目标飞行器的历史轨迹特征提取器。该模型具有前向传播速度快、结构复杂度低、特征提取效率高的特点,在自然语言等序列型数据处理任务中取得了良好的效果。放缩点积注意力[16]是构建Transformer 模型的基础,其计算公式为
式中:Q代表查询(Query)矩阵;K代表键值(Key)矩阵;V代表值(Value)矩阵;dk代表矩阵Q与K的维度,用于控制点积值的范围。进一步地,由多组放缩点积注意力机制所组成的多头注意力机制如图3 所示。
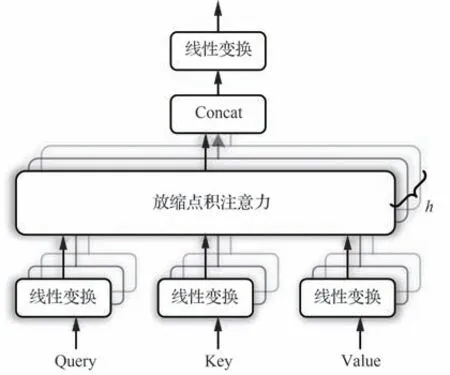
图3 多头注意力机制示意图Fig. 3 Diagram of multi-head attention mechanism
在多头注意力机制中,h组不同的Query、Key 和Value 矩阵被分别计算放缩点积注意力(Scaled Dot-Product Attention)后,通过矩阵拼接和线性变换获得最终的输出。每一组矩阵所关注的轨迹块均有所不同,通过多次的注意力处理,能够实现对P(t)的特征提取和表达。在计算过程中,第i个注意力头headi可表示为
式中:Qi、Ki和Vi分别代表注意力头headi所对应的Query、Key 和Value 矩阵。则多头注意力机制可表示为
式中:WO代表线性变换系数矩阵。
Transformer 模型是在多头注意力的基础上添加了求和、归一化、多层感知机等结构,如图4所示。该结构的编码器由N层网络堆叠而成,每层网络包含编码器与解码器结构。其中编码器中包含有多头注意力机制和前馈神经网络2 个子层,而解码器中的每一层包含带遮罩的多头注意力机制、编码-解码多头注意力机制和前馈神经网络。

图4 Transformer 模型结构示意图Fig. 4 Structure diagram of Transformer model
编码器的输入嵌入为轨迹序列经过块分割处理后的输入矩阵I(t),而解码器的输出嵌入为轨迹预测算法输出与目标下一时刻真实位置p(t+1)的矢量差。该模型的优势在于能够最大限度地减少对于外部信息的依赖,将算力聚焦于序列数据自身的关联信息中。
2. 2 基于Transformer 的预测误差补偿模型
本文所提出的预测误差补偿模型在Transformer 模型的基础上进行设计,主要包括轨迹序列的块分割、Transformer 模型特征提取、多层感知机回归等步骤,结构框图如图5 所示。
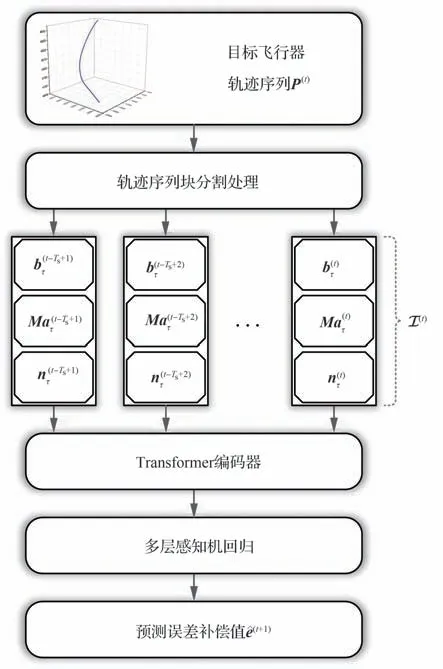
图5 轨迹预测误差补偿模型结构图Fig. 5 Structural diagram of trajectory prediction error compensation model
预测误差补偿模型首先对态势序列P(t)中的每一帧轨迹进行块分割处理后,变换成Transformer 编码器的输入矩阵I(t),具体表示为
式中:δ表示预测步长。
输入矩阵I(t)被传入至Transformer 编码器中,设定矩阵通道数为1,宽和高分别为1 和9。编码器中共有12 个注意力头,能够对序列中的块特征进行有效提取,其结果被6 层全连接神经网络所构成的多层感知机所处理。多层感知机为3输出神经网络,分别对应Oxyz坐标系下3 个分方向归一化后的补偿值,即
多层感知机的输出为归一化后3 个方向的补偿值,其实际误差补偿值的求取方法为
式中:ct代表目标飞行器所在位置的声速。
2. 3 动态误差补偿系数计算方法
在对目标飞行器的轨迹预测过程中,大过载机动通常会带来更大的基准预测值误差。同理,在目标飞行器处于平稳飞行的阶段,基准预测值则更为准确,甚至几乎没有误差。因此,在对基准预测值可能产生的误差补偿过程中,需要根据目标飞行器的机动状态,对误差补偿值进行动态调整。本文在目标飞行器的位置序列的基础上,提出频域空间下误差补偿系数计算方法,以区分大过载机动阶段与平稳飞行阶段,进一步提升目标飞行器轨迹预测误差补偿精度。
目标飞行器的轨迹序列能够通过离散傅里叶变换(Discrete Fourier Transform,DFT)方法,从时域表达转换为复指数形式的频域表达。考虑到DFT 的实时性限制,本文选用快速傅里叶变换(Fast Fourier Transform,FFT)方法求取飞行器轨迹序列的频域表达形式。针对t时刻目标飞行器在Oxyz坐标系下3 个分方向的位置序列,其中ξ∈{x,y,z},通过FFT 处理,其在频域空间上的复指数形式可表示为
由于FFT 的结果具有对称性,式(10)中仅取结果的前半部分进行计算。在最大模值的基础上,误差补偿系数σ(t+1)的计算方法可表示为
式中:η代表放缩系数。式(11)可以求取t时刻下所有分方向位置序列中频率大于κ的分量的最大模值,并通过线性放缩获得误差补偿系数σ(t)。误差补偿后的轨迹预测值可表示为
3 仿真与分析
为验证所提出的轨迹预测误差算法的有效性和先进性,本文采用飞行员在模拟器上一对一格斗所产生的数据集上对算法进行测试。空战数据集由2 种类型的数据组成:低速数据集(数据集编号Ⅰ)和高速数据集(数据集编号Ⅱ),其详细信息如表1 所示。

表1 空战数据集信息Table 1 Information of air combat dataset
试验所采用的2 种数据集分别由2 种不同型号的飞行器所生成,其中低速数据集对应螺旋桨式飞行器,而高速数据集对应喷气式飞行器。实验计算机的配置为 Intel i7-9700F CPU,NVIDIA RTX 2070S GPU,32 GB 运行内存。仿真试验的系统环境为Windows 10,利用Python 语言在Pytorch 框架下实现。
试验过程中,设置预测所用轨迹序列长度Ts=128,采样间隔Δt=100 ms,目标飞行器所在位置声速ct≡340 m/s,误差补偿系数频率阈值κ=1 Hz,放缩系数η=0.02。模型训练过程中选取L2 损失函数和Adam 优化器,学习率设置为0.001。试验中用于模型训练(包括轨迹预测模型及误差补偿模型)的数据占比85%,验证数据占比10%,测试数据占比5%。由于本文重点研究飞行器轨迹预测误差补偿方法,除3.1 节外均采用匀加速(Constant Acceleration,CA)运动模型作为基准预测值生成策略,即
3. 1 误差补偿模型性能总体评估
为更客观地验证本文所提出的TFPEC 方法的通用性,本节中选用不同飞行器轨迹预测算法作为基准预测值生成策略,分别对不同数据集下不同预测步长的场景进行测试。所选用的轨迹预测算法包括基于CA 运动模型的预测算法(Constant Acceleration Prediction Method CAPM)、基于卡尔曼滤波的轨迹预测(Kalman Filter-based Trajectory Prediction,KFTP)算法[20]、基于长短时记忆网络的战场目标轨迹预测(Prediction of Battle Target Trajectory based on LSTM,PBTT-LSTM)算法[21]以及输出-输入反馈艾尔曼(Output-Input Feedback Elman,OIF-Elman)网络预测算法[22],结果如表2 所示。表中预测精度提升百分比指引入误差补偿模型后,预测结果降低的平均绝对误差(Mean Absolute Error,MAE)与基准预测值MAE 的比值。
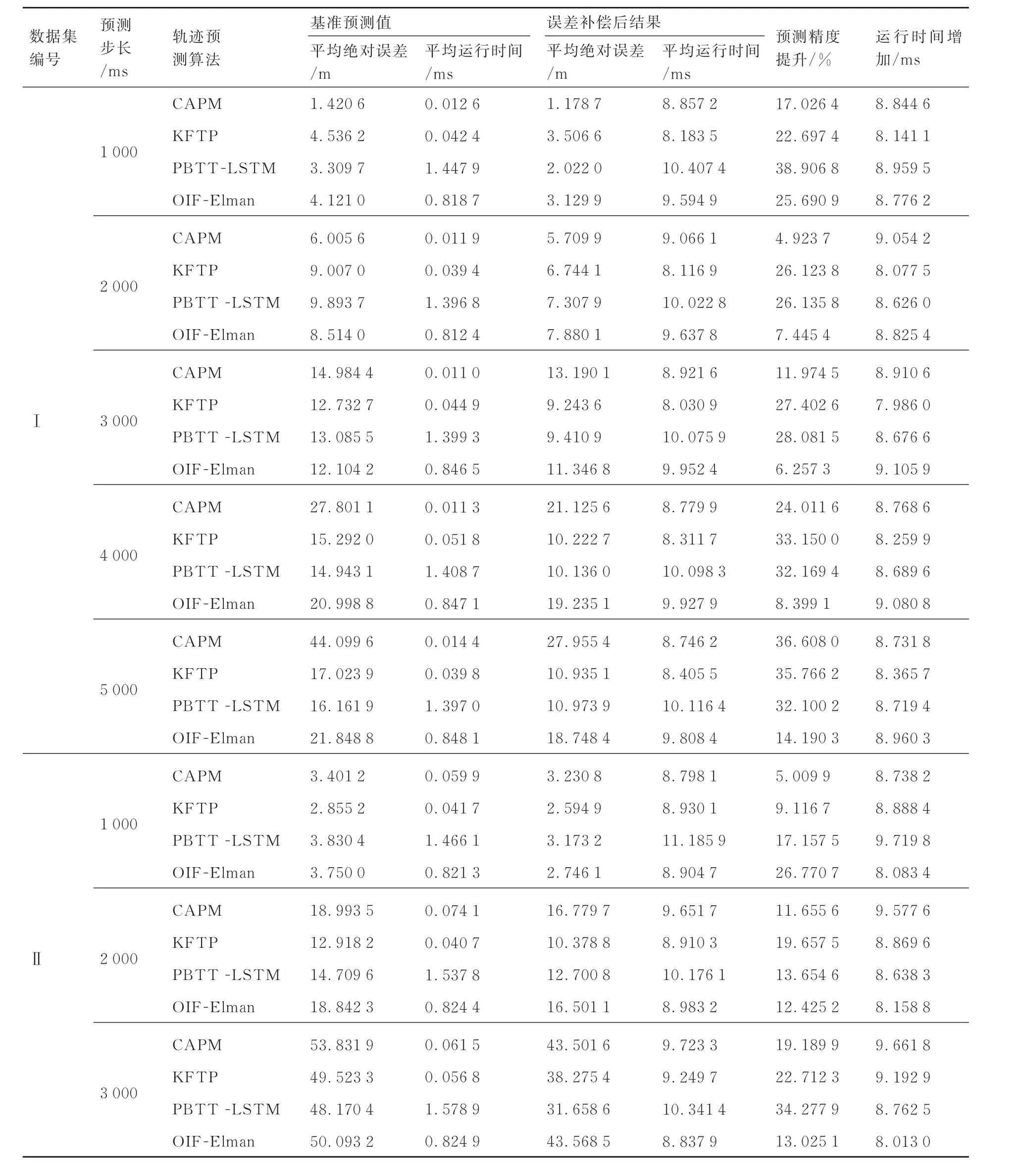
表2 基于Transformer 模型的预测误差补偿方法性能总体评估Table 2 Overall evaluation of performance of Transformer-based prediction error compensation method
对表2 进行分析,可得到如下结论:
1)从基准预测值和误差补偿后结果的比较中可以得出,本文所提出的误差补偿模型能够有效地提升各类轨迹预测算法的预测精度,且能够应用于不同飞行速度、不同预测步长的场景中。
2)通过分析不同预测步长的结果可以得出,误差补偿模型的作用效果随着预测步长的增大而增加,其中对OIF-Elman 轨迹预测算法在预测步长为5 000 ms 时的作用效果最为明显,在数据集Ⅱ中的预测精度提升46.061 1%。
3)通过分析运行时间增加的毫秒数可以得出,轨迹预测过程在引入误差补偿模型后,平均运行时间增加了8.731 7 ms。 其中PBTTLSTM 轨迹预测算法对应的轨迹预测过程平均耗时最久,为10.235 7 ms。因此,在引入误差补偿模型后,针对目标轨迹预测的频率仍然能够在50 Hz 以上。
3. 2 误差补偿方法性能对比
为测试本文所提TFPEC 方法的性能,本节中选取若干已有的误差补偿算法作为比较对象,测试对比的误差补偿算法包括文献[12]中所述的BPNN 算法以及文献[13]中所述的基于GRU的误差补偿算法,并记录其平均绝对误差、精度提升百分比以及运行时间,对比结果如表3 所示。
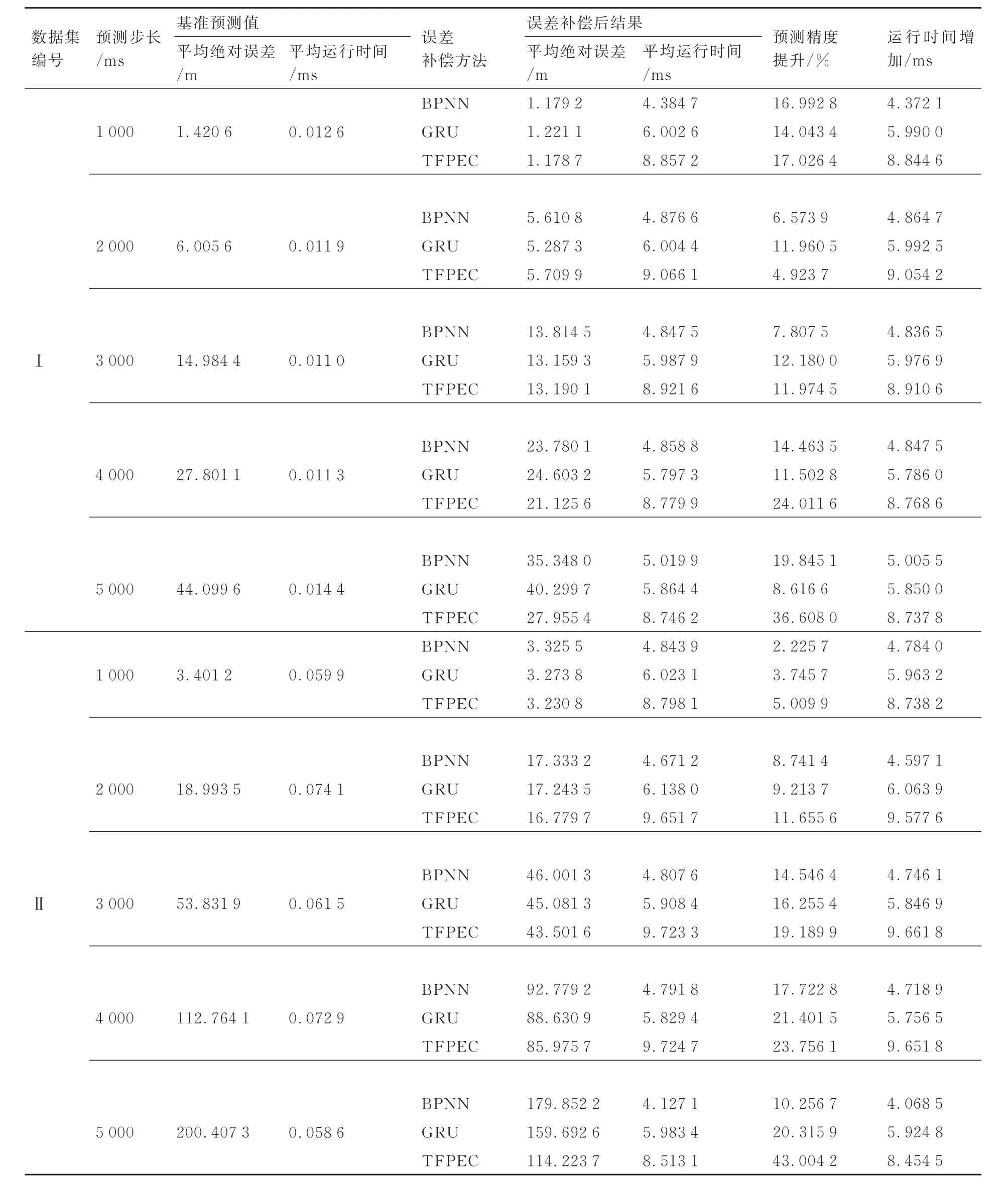
表3 误差补偿方法性能对比Table 3 Comparison of performance of error compensation methods
表3 中的所有数据均采用CAPM 作为基准预测值生成策略,对其进行分析可得出以下结论:
1)3 种误差补偿方法运行所消耗的时间较为接近,其中BPNN 方法平均消耗时间最短,为4.684 1 ms,而本文所提出的TFPEC 方法平均消耗时间最长,为9.039 4 ms。
2)在本文所涉及的2 类轨迹数据集中的5 种不同的预测步长下,3 种方法的引入均能有效提高轨迹预测结果的精度。在高速数据集中5 000 ms步长的预测任务中,TFPEC 方法能够将预测精度提升43.004 2%,远高于BPNN 和GRU 误差补偿算法。
3)本文所提出的TFPEC 方法能够在消耗时间可控的前提下,显著提高目标飞行器轨迹预测结果的精度。
3. 3 误差补偿系数有效性测试
为验证所提出的误差补偿系数的有效性和必要性,本节中首先对不同误差补偿系数下的预测结果MAE 进行测试,其结果如图6所示。
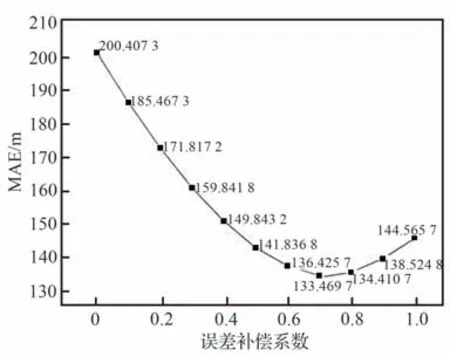
图6 各误差补偿系数下的预测结果MAEFig. 6 Mean absolute error of prediction result for each error compensation coefficient
由图6 可以看出,由Transformer 模型直接计算得出的误差补偿值并不能取得最优补偿效果。因此,需要在TFPEC 方法中引入动态误差补偿系数,以提高目标飞行器轨迹预测误差补偿的效果。
为进一步验证本文提出的误差补偿系数计算方法的合理性,在高速数据集中取100 s轨迹,绘制预测步长为5 000 ms 时未引入误差补偿系数时的MAE,以及其对应轨迹点频域上>1 Hz 的各个分量的最大模值,如图7 所示。图中,实线为未引入TFPEC 方法时的MAE 变化曲线,而虚线为模值变化曲线。对2 条曲线进行相关性计算,其Pearson 相关系数为0.198 421,Spearman 相关系数为0.172 85。因此可以认为,轨迹预测的MAE 精度与轨迹频域上的最大模值具有一定程度的相关性,利用轨迹频域的最大模值求取出的误差补偿系数能够帮助算法进一步地提高精度。

图7 预测误差与轨迹高频分量最大模值曲线图Fig. 7 Curves of prediction error and trajectory highfrequency component maximum modulus
频率阈值κ也显著地影响着TFPEC 方法的补偿效果。为验证本文所提方法中阈值选取的必要性和最优性,对不同频率阈值条件下的TFPEC方法所获得的轨迹预测值MAE 进行测试,结果如表4 所示。由表中数据可知,在频率阈值κ=1 Hz时,TFPEC 方法能够获得最优轨迹的补偿效果。

表4 各频率阈值下的预测结果MAETable 4 MAE of prediction result for each frequency threshold
3. 4 轨迹预测实例
本节试验中,分别在数据集Ⅰ和数据集Ⅱ上,利用CAPM 基准预测值生成方法,在预测步长为1 000 ms、2 000 ms、3 000 ms、4 000 ms、5 000 ms 的场景下进行仿真,并绘制预测结果,如图8~图11 所示。

图8 数据集I 预测结果三维示意图Fig. 8 3D schematic diagram of prediction results of dataset I

图9 数据集Ⅱ预测结果三维示意图Fig. 9 3D schematic diagram of prediction results of dataset Ⅱ
CAPM 基准预测值生成方法的特点是:飞行器在平稳机动时能够获得较为准确的预测值,而在大过载机动时则会出现预测误差较大的情况。由图10、图11 可知,TFPEC 方法能够维持CAPM 方法在目标飞行器平稳机动时的预测准确性,同时显著降低在大过载机动时的预测误差。这是由于动态误差补偿系数的引入,能够在平稳机动时对过大的误差补偿值进行抑制,优化了TFPEC 方法的性能。因此,本文所提TFPEC 方法能够广泛适用于多种运动特性的目标飞行器,且均能取得较好的预测效果。
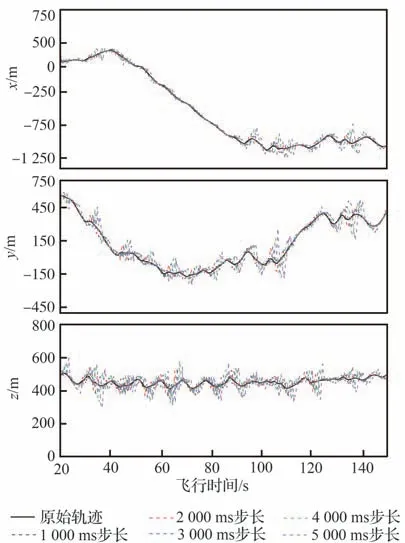
图10 数据集Ⅰ预测结果二维示意图Fig. 10 2D schematic diagram of prediction results of dataset I
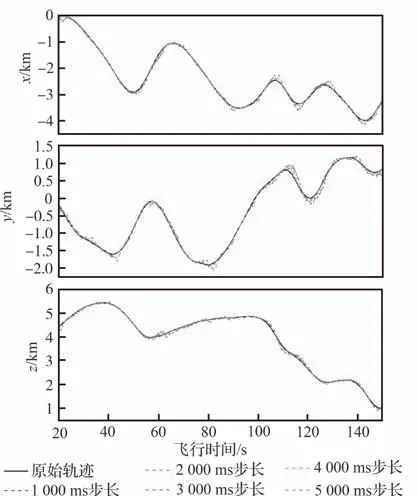
图11 数据集Ⅱ预测结果二维示意图Fig. 11 2D schematic diagram of prediction results of dataset Ⅱ
4 结 论
本文针对空战环境中的轨迹预测问题,提出了一种基于Transformer 模型的预测误差补偿方法。首先将飞行器的历史轨迹序列进行块分割处理,然后基于Transformer 设计了误差补偿模型,最后根据求取的误差补偿值特点,提出了误差补偿系数计算方法。通过实验验证得出以下结论:
1)相较于其他误差补偿方法,自注意力机制的引入使TFPEC 方法具有更高效的轨迹特征提取能力,与基于BPNN 和GRU 的方法相比,能够在消耗时间可控的条件下获得更为可信的轨迹预测误差补偿值。
2)目标飞行器历史轨迹序列中,频率>1 Hz 的高频分量最大模值与预测误差值具有相关性。本文所提出的基于傅里叶变换的动态误差补偿系数能够一定程度上描述目标飞行器的机动特性,从而进一步提升轨迹预测误差补偿的准确性。
3)本文所提出的TFPEC 方法具有较强的通用性,能够针对各类轨迹预测算法的误差进行有效修正。实验证明,在引入TFPEC 方法后,预测结果的精度相比原有算法至少提高了4.923 7%。在预测步长为5 000 ms 的高速数据集中,在OIFElman 预测算法的基础上,TFPEC 方法的引入能使预测结果精度提高至46.061 1%。
随着无人机技术的不断发展,其高性能、大过载的特点将对现有方法的准确性和泛化性带来更大的挑战。在接下来的工作中,需要结合作战样式、空战战术决策等相关理论进行研究,以缩小轨迹预测的解空间的方式,进一步提高预测结果的精度和可信性。

